Deterministic Scheduling Algorithm With Priority Classification for Industrial Wireless Networks
-
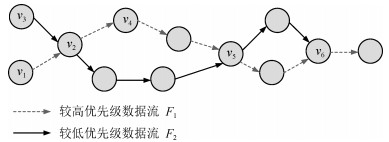
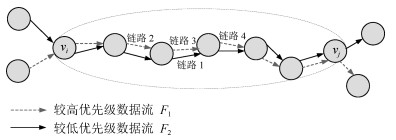
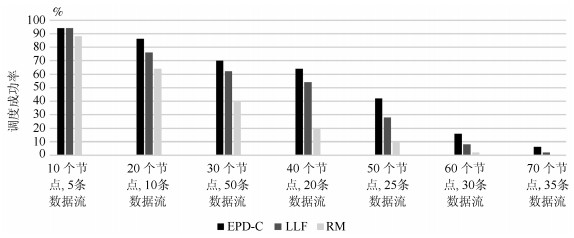
摘要: 确定性调度技术对于工业无线网络数据的实时性和确定性传输有着重要意义.本文针对工业无线网络数据流本身存在优先级分类属性的情况, 基于多信道时分多址接入(TDMA)技术, 在分析高优先级数据流对低优先级数据流造成的链路冲突延时和信道竞争延时基础上, 对网络进行调度预处理, 进而排除参数不合理的网络, 并向网络管理者反馈.对于通过预处理的网络, 调度算法优先为高优先级数据流的链路分配时隙和信道资源, 而对属于同一类优先级的数据流, 提出一种基于比例冲突空余时间的调度方案, 在满足可调度性条件的前提下, 根据各链路的比例冲突空余时间值从小到大依次分配时隙和信道资源.实验结果表明, 所提出的调度算法可以取得较高的网络调度成功率.Abstract: Deterministic scheduling technology has a significant impact on the real-time and deterministic data transmission in industrial wireless networks. This paper considers the case that end-to-end flows in industrial wireless networks have a property of priority classification, and adopt multi-channel time division multiple access (TDMA) technology. On the basis of analyzing the delays of lower priority flows due to both link conflict and channel contention caused by higher priority flows, there is a pre-processing scheduling for testing networks firstly. Therefore, some networks with unreasonable parameters can be excluded, and this will inform network administrator for further processing. For networks passing the test of pre-processing scheduling, the scheduling algorithm gives preference to allocate time slots and channels to link with higher priority flows. For the flows with the same priority, a scheduling scheme based on proportional deadline and conflict is also presented, which allocates the time slots and channels according to the values of proportional deadline and conflict in ascending order for flows that meet the schedulability condition. Results show that the proposed scheduling method can achieve a higher schedulable ratio.
-
Key words:
- Industrial wireless networks /
- deterministic scheduling /
- priority classification /
- pre-processing scheduling
1) 本文责任编委 付俊 -
表 1 模型中参数符号代表的意义
Table 1 Notations used in the considered model
符号 意义 Fi 第i条数据流 Ti 第i条数据流的周期 hp(Fi) 优先级高于Fi的所有数据流集合 Di 数据流Fi受到hp(Fi)影响造成的总延时 Ci 数据流Fi完成传输的截止时隙 Hi 数据流Fi端到端传输路径上的路由跳数 Li 数据流Fi的端到端传输延时 rHt 某条数据流在时隙t下剩余未传输的链路个数 表 2 三种调度方法的平均执行时间(ms)
Table 2 Average execution time of three scheduling methods (ms)
网络规模 10个节点,
5条数据流20个节点,
10条数据流30个节点,
15条数据流40个节点,
20条数据流50个节点,
25条数据流60个节点,
30条数据流70个节点,
35条数据流EPD-C 21.4 89.9 195.6 311.6 491.4 737.9 973.9 LLF 24.7 100.5 215.6 391.6 625.5 943.9 1 215.5 RM 26.5 113.3 269.4 483.6 859.3 1 340 2 084 -
[1] Sha M, Gunailaka D, Wu C J, Lu C Y. Empirical study and enhancements of industrial wireless sensor-actuator network protocols. IEEE Internet of Things Journal, 2017, 4(3): 696-704 doi: 10.1109/JIOT.2017.2653362 [2] Begum K, Dixit S. Industrial WSN using IoT: a survey. In: Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT). Palnchur, Chen Nai, India: IEEE, 2016. 499-504 [3] Wang Q, Jiang J. Comparative examination on architecture and protocol of industrial wireless sensor network standards. IEEE Communications Surveys & Tutorials, 2016, 18(3): 2197-2219 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7b14c25bc9010a525f25c11d6c1db59d [4] Toscano E, Lo Bello L. Multichannel superframe scheduling for IEEE 802.15.4 industrial wireless sensor networks. IEEE Transactions on Industrial Informatics, 2012, 8(2): 337-350 doi: 10.1109/TII.2011.2166773 [5] Saifullah A, Xu Y, Lu C Y, Chen Y X. Real-time scheduling for wirelessHART networks. In: Proceedings of the 31st IEEE Real-Time Systems Symposium (RTSS). San Diego, CA, USA: IEEE, 2010. 150-159 [6] Kim Y G, Lee M J. Scheduling multi-channel and multi-timeslot in time constrained wireless sensor networks via simulated annealing and particle swarm optimization. IEEE Communications Magazine, 2014, 52(1): 122-129 doi: 10.1109/MCOM.2014.6710073 [7] Kang H, Zhao Y N, Mei F. A graph coloring based TDMA scheduling algorithm for wireless sensor networks. Wireless Personal Communications, 2013, 72(2): 1005-1022 doi: 10.1007/s11277-013-1052-9 [8] Kang B, Nguyen P K H, Zalyubovskiy V, Choo H. A distributed delay-efficient data aggregation scheduling for duty-cycled WSNs. IEEE Sensors Journal, 2017, 17(11): 3422-3437 doi: 10.1109/JSEN.2017.2692246 [9] 贾杰, 代恩亮, 陈剑, 王兴伟, 赵林亮.无线传感器网络中联合路由优化的高能效链路调度.电子学报, 2014, 42(6): 1118-1124 doi: 10.3969/j.issn.0372-2112.2014.06.013Jia Jie, Dai En-Liang, Chen Jian, Wang Xing-Wei, Zhao Lin-Liang. Energy-efficient link scheduling combined with routing optimization in wireless sensor network. Acta Electronica Sinica, 2014, 42(6): 1118-1124 doi: 10.3969/j.issn.0372-2112.2014.06.013 [10] 牛建军, 邓志东.基于马尔可夫链的无线传感器网络分布式调度方法.自动化学报, 2010, 36(5): 685-695 doi: 10.3724/SP.J.1004.2010.00685Niu Jian-Jun, Deng Zhi-Dong. Markov chain-based distributed scheduling approach for wireless sensor network. Acta Automatica Sinica, 2010, 36(5): 685-695 doi: 10.3724/SP.J.1004.2010.00685 [11] Sgora A, Vergados D J, Vergados D D. A survey of TDMA scheduling schemes in wireless multihop networks. ACM Computing Surveys, 2015, 47(3): 1-39 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=84249ad24dcfe9401e41c7781eade0a7 [12] 张晓玲, 梁炜, 于海斌, 封锡盛.无线传感器网络传输调度方法综述.通信学报, 2012, 33(5): 143-157 doi: 10.3969/j.issn.1000-436X.2012.05.019Zhang Xiao-Ling, Liang Wei, Yu Hai-Bin, Feng Xi-Sheng. Survey of transmission scheduling methods in wireless sensor networks. Journal on Communications, 2012, 33(5): 143-157 doi: 10.3969/j.issn.1000-436X.2012.05.019 [13] Rao S, Keshri S, Gangwar D, Sundar P, Geetha V. A survey and comparison of GTS allocation and scheduling algorithms in IEEE 802.15.4 wireless sensor networks. In: Proceedings of the 2013 IEEE Conference on Information and Communication Technologies (ICT). Thuckalay, Tamil Nadu, India: IEEE, 2013. 98-103 [14] 李金宝, 王蒙, 郭龙江. MR-MC无线传感器网络最小延迟数据聚集调度研究.通信学报, 2014, 35(10): 192-199 doi: 10.3969/j.issn.1000-436x.2014.10.022Li Jin-Bao, Wang Meng, Guo Long-Jiang. Minimum latency data aggregation scheduling in MR-MC wireless sensor networks. Journal on Communications, 2014, 35(10): 192-199 doi: 10.3969/j.issn.1000-436x.2014.10.022 [15] 牛建军, 邓志东, 李超.无线传感器网络分布式调度方法研究.自动化学报, 2011, 37(5): 517-528 doi: 10.3724/SP.J.1004.2011.00517Niu Jian-Jun, Deng Zhi-Dong, Li Chao. Distributed scheduling approaches in wireless sensor network. Acta Automatica Sinica, 2011, 37(5): 517-528 doi: 10.3724/SP.J.1004.2011.00517 [16] 王恒, 陈鹏飞, 王平.面向WIA-PA工业无线传感器网络的确定性调度算法.电子学报, 2018, 46(1): 68-74 doi: 10.3969/j.issn.0372-2112.2018.01.010Wang Heng, Chen Peng-Fei, Wang Ping. Deterministic scheduling algorithms for WIA-PA industrial wireless sensor networks. Acta Electronica Sinica, 2018, 46(1): 68-74 doi: 10.3969/j.issn.0372-2112.2018.01.010 [17] 王恒, 李敏, 刘其琛, 王平.一种基于确定性调度的工业无线网络路由算法.仪器仪表学报, 2011, 32(9): 1921-1928 http://d.old.wanfangdata.com.cn/Periodical/yqyb201109001Wang Heng, Li Min, Liu Qi-Chen, Wang Ping. Routing algorithm for industrial wireless network based on deterministic scheduling. Chinese Journal of Scientific Instrument, 2011, 32(9): 1921-1928 http://d.old.wanfangdata.com.cn/Periodical/yqyb201109001 [18] Saifullah A, Xu Y, Lu C Y, Chen Y X. End-to-end communication delay analysis in industrial wireless networks. IEEE Transactions on Computers, 2015, 64(5): 1361-1374 doi: 10.1109/TC.2014.2322609 [19] Industrial networks - Wireless communication network and communication profiles - WIA-PA, IEC 62601, 2015 [20] Leung J Y, Whitehead J. On the complexity of fixed-priority scheduling of periodic, real-time tasks. Performance Evaluation, 1982, 2(4): 237-250 doi: 10.1016/0166-5316(82)90024-4 [21] 王永吉, 陈秋萍.单调速率及其扩展算法的可调度性判定.软件学报, 2004, 15(6): 799-814 http://d.old.wanfangdata.com.cn/Periodical/rjxb200406002Wang Yong-Ji, Chen Qiu-Ping. On schedulability test of rate monotonic and its extendible algorithms. Journal of Software, 2004, 15(6): 799-814 http://d.old.wanfangdata.com.cn/Periodical/rjxb200406002 [22] Ayele A A, Rao V S, Dileep K G, Bokka R K. Combining EDF and LST to enhance the performance of real-time task scheduling. In: Proceedings of the 2016 International Conference on ICT in Business, Industry, and Government (ICTBIG). Indore, India: IEEE, 2016. -




 下载:
下载: