A Contour Detection Method Based on Visual Perception Mechanism in Primary Visual Pathway
-
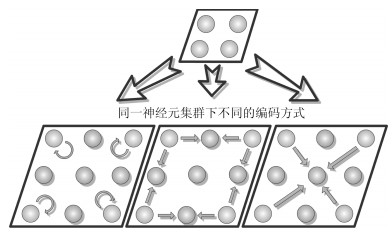
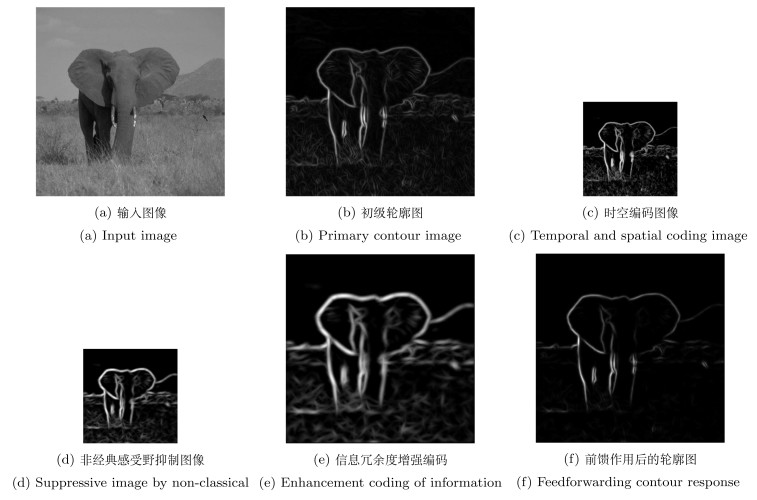
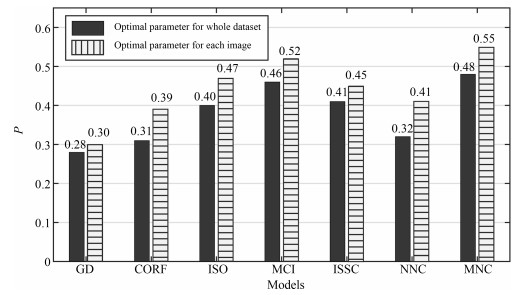
摘要: 考虑到初级视通路中视觉信息传递和处理过程中的特点, 本文提出了一种基于视觉感知机制的轮廓检测新方法.构建视觉信息局部细节检测与整体轮廓感知的不同路径.利用高斯导函数提取初级轮廓响应; 构建神经网络, 利用时空编码提高主体轮廓对比度; 然后, 利用非经典感受野的侧抑制作用抑制纹理背景; 另外, 针对轮廓信息强化以及检测鲁棒性的要求, 在视辐射区提出了一种信息冗余度增强编码机制; 最后, 将初级轮廓直接前馈至初级视皮层, 以达到轮廓响应的快速调节和完整性融合.以RuG40图库为实验对象, 经过非极大值抑制和阈值处理, 得到的轮廓二值图与基准轮廓图比较, 在整个数据集中的最优平均$P$指标和每张图的最优平均$P$指标分别为0.48和0.55, 并且FPS达到了1/2.结果表明本文方法能有效突出主体轮廓并抑制纹理背景, 为后续图像理解和分析提供了一种新的思路.Abstract: A new method of contour detection is proposed in this paper according to the characteristics of visual information transmission and processing which is based on visual perception mechanism in human primary visual pathway. Firstly, the spatio-temporal coding of neural information is realized on the basis of the Gaussian derivative function, and then the texture and background are suppressed by the non-classical receptive field. In addition, we propose a neural coding that can strengthen the redundancy of visual information in the optic radiation area to enhance the contour information and robustness of detecting. Finally, primary contour is fed forward to the primary visual cortex to achieve rapid adjustment of the contour response. In this paper, the RuG40 library is taken for processing, acquiring the contour detecting result through the non-maximal suppression and hysteresis threshold, and mean values $P$ of optimal parameters for whole dataset and each image are 0.48 and 0.55, respectively, compared with the ground truth. In addition, the FPS of algorithm reaches 1/2. The results indicate the new method in this paper can effectively highlight the principal contour and suppress texture region which will provide a new idea for subsequent image comprehension and analysis.
-
Key words:
- Contour detection /
- spatio-temporal coding /
- enhancement coding of information redundancy /
- feed forward
1) 本文责任编委 刘跃虎 -
图 4 RuG40图库中的轮廓测试结果(第1行为用于测试的自然场景图; 第2行为基准轮廓图; 第3行为GD检测结果; 第4行为CORF检测结果; 第5行为ISO检测结果; 第6行为MCI检测结果; 第7行为ISSC检测结果; 第8行为NNC检测结果; 第9行为MNC检测结果)
Fig. 4 Contour test results of the RuG40 gallery (The first line is the input of natural scene images; The second line is the contour baselines; The third line is the results of GD; The fourth line is the results of CORF; The fifth line is the results of ISO; The sixth line is the results of MCI; The seventh line is the results of ISSC; The eighth line is the results of NNC; The ninth line is the results of MNC)
图 6 随机选取的6组图像在多组参数下检测结果的$P$值盒须图统计(I表示ISO方法, C表示MCI方法, S表示ISSC方法, N表示NNC方法, M表示MNC方法)
Fig. 6 Box-and-Whisker plots of the performance of the ISO (denoted by I), the MCI (denoted by C), the ISSC (denoted by S), the NNC (denoted by N), and the MNC (denoted by M) for six random test images of multiparameters
表 1 图 4中不同方法的参数设置, 性能指标及运行速度.
Table 1 Parameters, speed and performance of the different methods in Fig. 4
图像 算法 $\alpha$ $p$ ${e_{FP}}$ ${e_{FN}}$ $P$ $\rm FPS$ GD 0.20 1.50 0.13 0.30 4 CORF 0.20 0.42 0.30 0.50 3/5 ISO 0.80 0.20 0.25 0.38 0.55 3 buffalo MCI 0.70 0.30 0.18 0.29 0.59 1/22 ISSC 0.10 0.22 0.27 0.58 1/8 NNC 0.20 0.10 0.22 0.32 0.54 1 MNC 0.10 0.30 0.21 0.27 0.64 1/2 GD 0.10 1.29 0.25 0.39 CORF 0.20 0.32 0.29 0.52 ISO 1.00 0.10 0.37 0.32 0.53 elephant 2 MCI 0.40 0.30 0.22 0.30 0.58 ISSC 0.10 0.25 0.30 0.56 NNC 0.20 0.30 0.28 0.30 0.56 MNC 0.10 0.20 0.13 0.36 0.62 GD 0.25 1.33 0.18 0.45 CORF 0.20 0.41 0.29 0.50 ISO 0.60 0.20 0.29 0.27 0.58 golf cart MCI 0.90 0.40 0.23 0.28 0.62 ISSC 0.3 0.30 0.30 0.55 NNC 0.10 0.30 0.27 0.29 0.57 MNC 0.10 0.40 0.26 0.24 0.62 GD 0.25 1.33 0.18 0.45 CORF 0.30 0.55 0.14 0.58 ISO 0.90 0.10 0.21 0.27 0.61 hyena MCI 0.60 0.50 0.19 0.22 0.65 ISSC 0.20 0.28 0.24 0.59 NNC 0.20 0.20 0.30 0.24 0.59 MNC 0.10 0.20 0.21 0.27 0.64 GD 0.20 1.77 0.15 0.25 CORF 0.30 0.67 0.32 0.45 ISO 0.80 0.20 0.32 0.51 0.47 lions MCI 1.00 0.50 0.48 0.29 0.50 ISSC 0.3 0.45 0.30 0.48 NNC 0.30 0.30 0.45 0.31 0.47 MNC 0.70 0.40 0.45 0.28 0.51 -
[1] Mignotte M. A biologically inspired framework for contour detection. Pattern Analysis and Applications, 2017, 20(2): 365-381 doi: 10.1007/s10044-015-0494-y [2] Ding L J, Goshtasby A. On the Canny edge detector. Pattern Recognition, 2001, 34(3): 721-725 doi: 10.1016/S0031-3203(00)00023-6 [3] 蒋朝辉, 吴巧群, 桂卫华, 阳春华, 谢永芳.基于分数阶的多向微分算子的高炉料面轮廓自适应检测.自动化学报, 2017, 43(12): 2115-2126 doi: 10.16383/j.aas.2017.c160621Jiang Zhao-Hui, Wu Qiao-Qun, Gui Wei-Hua, Yang Chun-Hua, Xie Yong-Fang. Adaptive detection of blast furnace surface contour with fractional multi-directional differential operator. Acta Automatica Sinica, 2017, 43(12): 2115-2126 doi: 10.16383/j.aas.2017.c160621 [4] Arbelaez P, Maire M, Fowlkes C, Malik J. Contour detection and hierarchical image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 898-916 doi: 10.1109/TPAMI.2010.161 [5] Martin D R, Fowlkes C C, Malik J. Learning to detect natural image boundaries using local brightness, color, and texture cues. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(5): 530-549 doi: 10.1109/TPAMI.2004.1273918 [6] Young R A, Lesperance R M. The Gaussian derivative model for spatial-temporal vision: II. Cortical data. Spatial Vision, 2001, 14(3): 321-389 [7] Azzopardi G, Petkov N. A CORF computational model of a simple cell that relies on LGN input outperforms the Gabor function model. Biological Cybernetics, 2012, 106(3): 177-189 doi: 10.1007/s00422-012-0486-6 [8] Grigorescu C, Petkov N, Westenberg M A. Contour detection based on nonclassical receptive field inhibition. IEEE Transactions on Image Processing, 2003, 12(7): 729-739 doi: 10.1109/TIP.2003.814250 [9] Zeng C, Li Y J, Li C Y. Center-surround interaction with adaptive inhibition: a computational model for contour detection. NeuroImage, 2011, 55(1): 49-66 doi: 10.1016/j.neuroimage.2010.11.067 [10] Yang K F, Li C Y, Li Y J. Multifeature-based surround inhibition improves contour detection in natural images. IEEE Transactions on Image Processing, 2014, 23(12): 5020-5032 doi: 10.1109/TIP.2014.2361210 [11] 廖进文, 范影乐, 武薇, 高云园, 李轶.基于抑制性突触多层神经元群放电编码的图像边缘检测.中国生物医学工程学报, 2014, 33(5): 513-524 doi: 10.3969/j.issn.0258-8021.2014.05.01Liao Jin-Wen, Fan Ying-Le, Wu Wei, Gao Yun-Yuan, Li Yi. Image edge detection based on spike coding of multilayer neuronal population with inhibitory synapse. Chinese Journal of Biomedical Engineering, 2014, 33(5): 513-524 doi: 10.3969/j.issn.0258-8021.2014.05.01 [12] Chen M G, Yan Y, Gong X J, Gilbert C D, Liang H L, Li W. Incremental integration of global contours through interplay between visual cortical areas. Neuron, 2014, 82(3): 682-694 doi: 10.1016/j.neuron.2014.03.023 [13] Freud E, Plaut D C, Behrmann M. `What' is happening in the dorsal visual pathway. Trends in Cognitive Sciences, 2016, 20(10): 773-784 doi: 10.1016/j.tics.2016.08.003 [14] Taylor W R, Vaney D I. Diverse synaptic mechanisms generate direction selectivity in the rabbit retina. The Journal of Neuroscience, 2002, 22(17): 7712-7720 doi: 10.1523/JNEUROSCI.22-17-07712.2002 [15] Bays P M. A signature of neural coding at human perceptual limits. Journal of Vision, 2016, 16(11): 4 doi: 10.1167/16.11.4 [16] Zhu M C, Rozell C J. Visual nonclassical receptive field effects emerge from sparse coding in a dynamical system. PLoS Computational Biology, 2013, 9(8): e1003191 doi: 10.1371/journal.pcbi.1003191 [17] Yu Q, Tang H J, Tan K C, Li H Z. Rapid feedforward computation by temporal encoding and learning with spiking neurons. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(10): 1539-1552 doi: 10.1109/TNNLS.2013.2245677 [18] Hu J, Tang H J, Tan K C, Li H Z. How the brain formulates memory: a spatio-temporal model research frontier. IEEE Computational Intelligence Magazine, 2016, 11(2): 56-68 doi: 10.1109/MCI.2016.2532268 [19] Buonocore A, Caputo L, Pirozzi E, Carfora M F. A leaky integrate-and-fire model with adaptation for the generation of a spike train. Mathematical Biosciences and Engineering, 2016, 13(3): 483-493 doi: 10.3934/mbe.2016002 [20] Muhle-Karbe P S, Duncan J, De Baene W, Mitchell D J, Brass M. Neural coding for instruction-based task sets in human frontoparietal and visual cortex. Cerebral Cortex, 2017, 27(3): 1891-1905 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=9ed89e2bff4ffeffe9386fd3452382c7 [21] Tang J Y, Jimenez S C A, Chakraborty S, Schultz S R. Visual receptive field properties of neurons in the mouse lateral geniculate nucleus. PLoS One, 2016, 11(1): e0146017 doi: 10.1371/journal.pone.0146017 [22] 谢昭, 童昊浩, 孙永宣, 吴克伟.一种仿生物视觉感知的视频轮廓检测方法.自动化学报, 2015, 41(10): 1814-1824 doi: 10.16383/j.aas.2015.c150018Xie Zhao, Tong Hao-Hao, Sun Yong-Xuan, Wu Ke-Wei. Dynamic contour detection inspired by biological visual perception. Acta Automatica Sinica, 2015, 41(10): 1814-1824 doi: 10.16383/j.aas.2015.c150018 [23] 李智勇, 何霜, 刘俊敏, 李仁发.基于蛙眼R3细胞感受野模型的运动滤波方法.自动化学报, 2015, 41(5): 981-990 doi: 10.16383/j.aas.2015.c140810Li Zhi-Yong, He Shuang, Liu Jun-Min, Li Ren-Fa. Motion filtering by modelling R3 cell's receptive field in frog eyes. Acta Automatica Sinica, 2015, 41(5): 981-990 doi: 10.16383/j.aas.2015.c140810 -





 下载:
下载: