Design of Sparse Span-lateral Inhibition Neural Network Based on Connection Self-organization Development
-
摘要: 针对跨越——侧抑制神经网络（Span-lateral inhibition neural network，S-LINN）的结构调整及参数学习问题，结合生物神经系统中神经元的稀疏连接特性，依据儿童及青少年智力发展水平与大脑皮层发育之间的相互关系，提出以小世界网络连接模式进行初始稀疏化的连接自组织发育稀疏跨越——侧抑制神经网络设计方法.定义网络连接稀疏度及神经元输出贡献率，设计网络连接增长——修剪规则，根据智力超常组皮层发育与智力水平的对应关系调整和控制网络连接权值，动态调整网络连接实现网络智力的自组织发育.通过非线性动力学系统辨识及函数逼近基准问题的求解，证明在同等连接复杂度的情况下，稀疏连接的跨越——侧抑制神经网络具有更好的泛化能力.
-
关键词:
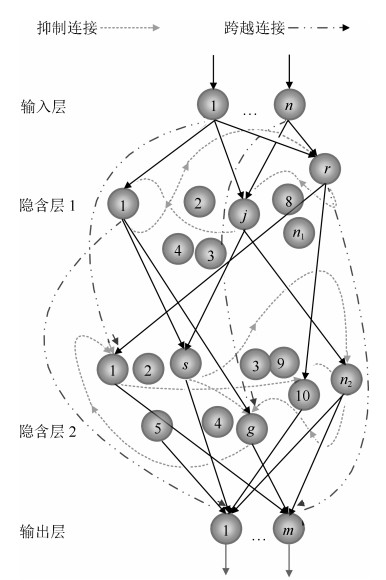
- 跨越-侧抑制神经网络 /
- 稀疏 /
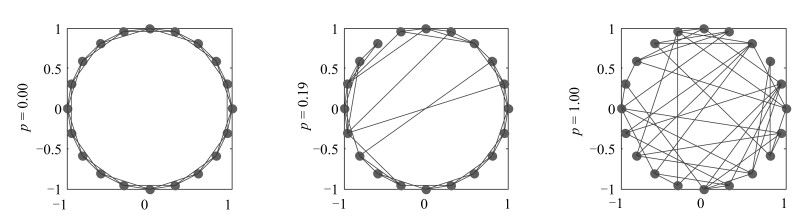
- 小世界网络 /
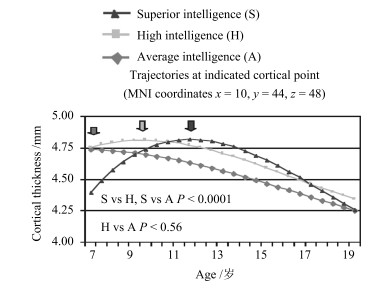
- 智力发展
Abstract: Inspired by the sparse connection of neurons in biological nervous system and the relationship between children and adolescents' intellectual ability and cortical development, a connection self-organization development-based sparse span-lateral inhibition neural network (sS-LINN) is developed to solve the structure adjustment and parameter learning problem, which adopts the small-world network connection mode as the initial sparse network architecture. A growing-pruning rule of network connection is designed to adjust and control the sparseness of network connections based on the definitions of connection sparseness and neuron output contribution rate. Performance of the proposed sparse S-LINN is evaluated successfully through simulation using nonlinear dynamic system identification and function approximation benchmark problems. It is shown that the proposed sS-LINN can produce a very compact structure with good generalization ability in comparison with other methods.1) 本文责任编委 王占山 -
图 1 全连接网络及稀疏连接网络
Fig. 1 Structural diagram of fully connected network and sparse connected network
图 5 CaseA:网络测试输出及学习误差曲线
Fig. 5 CaseA: Network output for test samples and the learning error curve
图 6 CaseB:网络测试输出及学习误差曲线
Fig. 6 CaseB: Network output for test samples and the learning error curve
图 7 CaseC:网络测试输出及学习误差曲线
Fig. 7 CaseC: Network output for test samples and the learning error curve
图 8 三次独立实验中前200次迭代中网络性能对比
Fig. 8 The comparison of network performance for the 3 independent runs (the first 200 iterations)
表 1 三次独立实验中网络性能及其权值连接变化情况
Table 1 Network performance and the dynamic adjustment process of connected weight
Method
(# Total connections)Training
MSETraining
RMSETesting
MSETesting
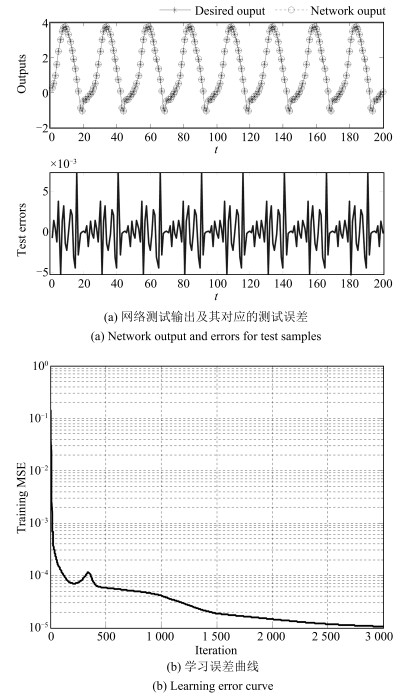
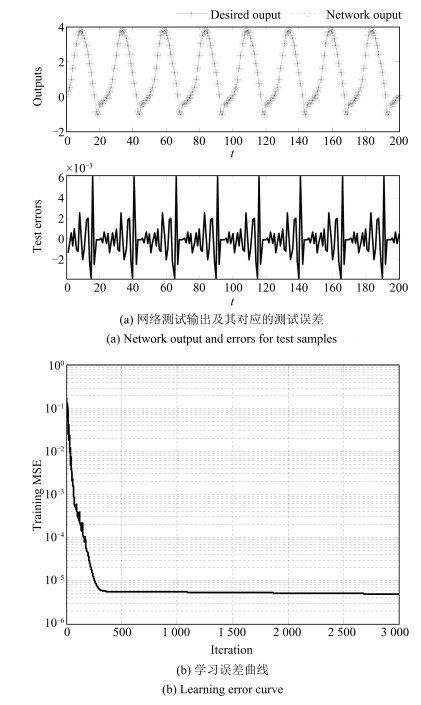
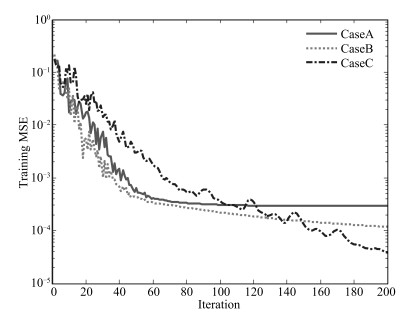
RMSECaseA: 43-50-39 2.06 $\times 10^{-5}$ 0.0045 1.96 $\times 10^{-5}$ 0.0044 CaseB: 43-51-39 1.05 $\times 10^{-5}$ 0.0032 4.01 $\times 10^{-5}$ 0.0063 CaseC: 43-51-38 4.88 $\times 10^{-6}$ 0.0022 3.67 $\times 10^{-6}$ 0.0019 
下载: 导出CSV
表 2 sS-LINN与其他神经网络方法的性能对比
Table 2 Network performance and the dynamic adjustment process of connected weight
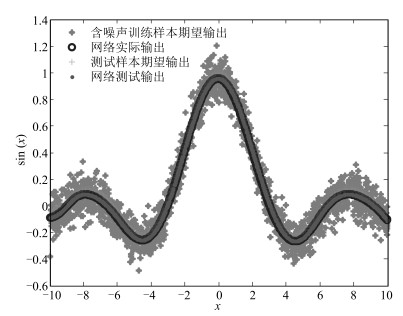
Method # Hidden neurons /connections Testing MSE Standard RBF[34] / 0.695 Standard SVR[33] / 0.445 SVR with prior knowledge[33] / 0.354 LCRBF[34] / 0.273 CP-NN[35] $2\to9$ 1.25 $\times 10^{-4}$ $20\to 10$ 1.04 $\times 10^{-4}$ AGPNNC[35] $2\to 10$ 1.71 $\times 10^{-4}$ $20\to10$ 1.23 $\times 10^{-4}$ S-LINN[25] 8 3.82 $\times 10^{-5}$ sS-LINN 39个连接权值 2.01 $\times 10^{-5}$
下载: 导出CSV
-
[1] Braitenberg V. Cortical architectonics:general and areal. Architectonics of the Cerebral Cortex. New York, USA:Raven Press, 1978. 443-465 [2] Paschke P, Möller R. Simulation of sparse random networks on a CNAPS SIMD neurocomputer. Neuromorphic Systems:Engineering Silicon from Neurobiology. Singapore:Scientific Press, 1998. 251-260 [3] Liu D R, Michel A N. Robustness analysis and design of a class of neural networks with sparse interconnecting structure. Neurocomputing, 1996, 12(1):59-76 doi: 10.1016/0925-2312(95)00040-2 [4] Gripon V, Berrou C. Sparse neural networks with large learning diversity. IEEE Transactions on Neural Networks, 2011, 22(7):1087-1096 doi: 10.1109/TNN.2011.2146789 [5] Guo Z X, Wong W K, Li M. Sparsely connected neural network-based time series forecasting. Information Sciences, 2012, 193:54-71 doi: 10.1016/j.ins.2012.01.011 [6] Wang J, Cai Q L, Chang Q Q, Zurada J M. Convergence analyses on sparse feedforward neural networks via group lasso regularization. Information Sciences, 2017, 381:250-269 doi: 10.1016/j.ins.2016.11.020 [7] Watts D J, Strogatz S H. Collective dynamics of "Small-World" networks. Nature, 1998, 393(6684):440-442 doi: 10.1038/30918 [8] Sporns O, Zwi J D. The small world of the cerebral cortex. Neuroinformatics, 2004, 2(2):145-162 doi: 10.1385/NI:2:2 [9] Bassett D S, Bullmore E. Small-world brain networks. The Neuroscientist, 2006, 12(6):512-523 doi: 10.1177/1073858406293182 [10] Ahn Y Y, Jeong H, Kim B J. Wiring cost in the organization of a biological neuronal network. Physica A:Statistical Mechanics and Its Applications, 2006, 367:531-537 doi: 10.1016/j.physa.2005.12.013 [11] Zheng P S, Tang W S, Zhang J X. A Simple method for designing efficient small-world neural networks. Neural Networks, 2010, 23(2):155-159 [12] Simard D, Nadeau L, Kröger H. Fastest learning in small-world neural networks. Physics Letters A, 2005, 336(1):8-15 doi: 10.1016/j.physleta.2004.12.078 [13] Lago-Fernández L F, Huerta R, Corbacho F, Sigüenza J A. Fast response and temporal coherent oscillations in small-world networks. Physical Review Letters, 2000, 84(12):2758-2761 doi: 10.1103/PhysRevLett.84.2758 [14] Morelli L G, Abramson G, Kuperman M N. Associative memory on a small-world neural network. The European Physical Journal B—Condensed Matter and Complex Systems, 2004, 38(3):495-500 [15] 王爽心, 杨成慧.基于层连优化的新型小世界神经网络.控制与决策, 2014, 29(1):77-82 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201401012Wang Shuang-Xin, Yang Cheng-Hui. Novel small-world neural network based on topology optimization. Control and Decision, 2014, 29(1):77-82 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201401012 [16] 伦淑娴, 林健, 姚显双.基于小世界回声状态网的时间序列预测.自动化学报, 2015, 41(9):1669-1679 http://www.aas.net.cn/CN/abstract/abstract18740.shtmlLun Shu-Xian, Lin Jian, Yao Xian-Shuang. Time series prediction with an improved echo state network using small world network. Acta Automatica Sinica, 2015, 41(9):1669-1679 http://www.aas.net.cn/CN/abstract/abstract18740.shtml [17] Erkaymaz O, Ozer M, Perc M. Performance of small-world feedforward neural networks for the diagnosis of diabetes. Applied Mathematics and Computation, 2017, 311:22-28 doi: 10.1016/j.amc.2017.05.010 [18] Peters A, Sethares C. Organization of pyramidal neurons in area 17 of monkey visual cortex. The Journal of Comparative Neurology, 1991, 306(1):1-23 doi: 10.1002/cne.903060102 [19] Markram H, Toledo-Rodriguez M, Wang Y, Gupta A, Silberberg G, Wu C Z. Interneurons of the neocortical inhibitory system. Nature Reviews Neuroscience, 2004, 5(10):793-807 doi: 10.1038/nrn1519 [20] Mountcastle V B. The columnar organization of the neocortex. Brain, 1997, 120(4):701-722 doi: 10.1093/brain/120.4.701 [21] Hubel D H, Wiesel T N. Sequence regularity and geometry of orientation columns in the monkey striate cortex. The Journal of Comparative Neurology, 1974, 158(3):267-293 doi: 10.1002-cne.901580304/ [22] Lübke J, Feldmeyer D. Excitatory signal flow and connectivity in a cortical column:focus on barrel cortex. Brain Structure and Function, 2007, 212(1):3-17 doi: 10.1007/s00429-007-0144-2 [23] Buxhoeveden D P, Casanova M F. The minicolumn hypothesis in neuroscience. Brain, 2002, 125(5):935-951 doi: 10.1093/brain/awf110 [24] Rockland K S, Ichinohe N. Some Thoughts on cortical minicolumns. Experimental Brain Research, 2004, 158(3):265-277 doi: 10.1007%2Fs00221-004-2024-9 [25] 杨刚, 乔俊飞, 薄迎春, 韩红桂.一种基于大脑皮层结构的侧抑制神经网络.控制与决策, 2013, 28(11):1702-1706 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201311017Yang Gang, Qiao Jun-Fei, Bo Ying-Chun, Han Hong-Gui. A lateral inhibition neural network based on neocortex topology. Control and Decision, 2013, 28(11):1702-1706 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201311017 [26] Yang G, Qiao J F. A fast and efficient two-phase sequential learning algorithm for spatial architecture neural network. Applied Soft Computing, 2014, 25:129-138 doi: 10.1016/j.asoc.2014.09.012 [27] Fiesler E. Comparative bibliography of ontogenic neural networks. In:Proceedings of the 1994 International Conference on Artificial Neural Networks. Sorrento, Italy:Springer, 1994. 793-796 [28] Elizondao D, Fiesler E, Korczak J. Non-ontogenic sparse neural networks. In:Proceedings of the 1995 IEEE International Conference on Neural Networks. Perth, WA, Australia:IEEE, 1995. 290-295 [29] Newman M E J, Watts D J. Renormalization group analysis of the small-world network model. Physics Letters A, 1999, 263(4-6):341-346 doi: 10.1016/S0375-9601(99)00757-4 [30] 王波, 王万良, 杨旭华. WS与NW两种小世界网络模型的建模及仿真研究.浙江工业大学学报, 2009, 37(2):179-182, 189 doi: 10.3969/j.issn.1006-4303.2009.02.014Wang Bo, Wang Wan-Liang, Yang Xu-Hua. Research of modeling and simulation on WS and NW small-world network model. Journal of Zhejiang University of Technology, 2009, 37(2):179-182, 189 doi: 10.3969/j.issn.1006-4303.2009.02.014 [31] Shaw P, Greenstein D, Lerch J, Clasen L, Lenroot R, Gogtay N, Evans A, Rapoport J, Giedd J. Intellectual ability and cortical development in children and adolescents. Nature, 2006, 440(7084):676-679 doi: 10.1038/nature04513 [32] Leng G, McGinnity T M, Prasad G. Design for self-organizing fuzzy neural networks based on genetic algorithms. IEEE Transactions on Fuzzy Systems, 2006, 14(6):755-766 doi: 10.1109/TFUZZ.2006.877361 [33] Lauer F, Bloch G. Incorporating prior knowledge in support vector regression. Machine Learning, 2008, 70(1):89-118 [34] Qu Y J, Hu B G. RBF networks for nonlinear models subject to linear constraints. In:Proceedings of the 2009 IEEE International Conference on Granular Computing. Nanchang, China:IEEE, 2009. 482-487 [35] Han H G, Qiao J F. A structure optimisation algorithm for feedforward neural network construction. Neurocomputing, 2013, 99:347-357 doi: 10.1016/j.neucom.2012.07.023 [36] Narendra K S, Parthasarathy K. Identification and control of dynamical systems using neural networks. IEEE Transactions on Neural Networks, 1990, 1(1):4-27 http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_89fcbba67ed6200b6b18dc26ecde7431 [37] Manngard M, Kronqvist J, Böling J M. Structural learning in artificial neural networks using sparse optimization. Neurocomputing, 2018, 272:660-667 doi: 10.1016/j.neucom.2017.07.028 -
图(9) / 表(3)
计量
- 文章访问数: 2469
- HTML全文浏览量: 346
- PDF下载量: 416
- 被引次数: 0
