-
摘要: 目前受限玻尔兹曼机网络训练算法主要是基于采样的算法.当用采样算法进行梯度计算时,得到的采样梯度是真实梯度的近似值,采样梯度和真实梯度之间存在较大的误差,这严重影响了网络的训练效果.针对该问题,本文首先分析了采样梯度和真实梯度之间的数值误差和方向误差,以及它们对网络训练性能的影响,然后从马尔科夫采样的角度对以上问题进行了理论分析,并建立了梯度修正模型,通过修正梯度对采样梯度进行数值和方向的调节,并提出了基于改进并行回火算法的训练算法,即GFPT(Gradient fixing parallel tempering)算法.最后给出GFPT算法与现有算法的对比实验,仿真结果表明,GFPT算法可以极大地减小采样梯度和真实梯度之间的误差,大幅度提升受限玻尔兹曼机网络的训练效果.Abstract: Currently, most algorithms for training restricted Boltzmann machines (RBMs) are based on multi-step Gibbs sampling. When the sampling algorithm is used to calculate gradient, the sampling gradient is an approximate value of the true gradient, and there is a big error between the sampling gradient and the true gradient, which seriously affects training effect of network. This article focuses on the problems mentioned above. Firstly, numerical error and direction error between gradient and true gradient sampling are analyzed, as well as their influences on the performance of network training. The problems are theoretically analyzed from the angle of Markov sampling. Then a gradient modification model is established to adjust the numerical value and direction of sampling gradient. Furthermore, improved tempering learning based algorithm is put forward, that is, GFPT (Gradient fixing parallel tempering) algorithm. Finally, a comparative experiment on the GFPT algorithm and existing algorithms is given. It demonstrated that GFPT algorithm can greatly reduce the sampling error between sampling gradient and true gradient, and improve RBM network training precision.1) 本文责任编委 乔俊飞
-
表 1 训练算法及参数
Table 1 Training algorithms and parameters

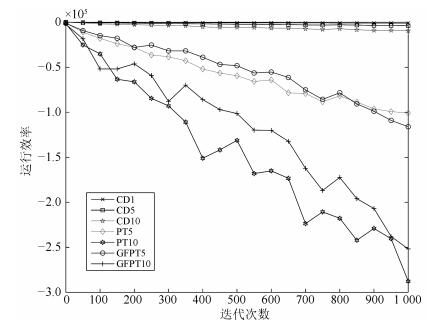
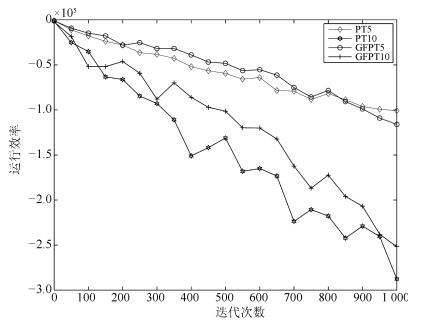
CD1 CD5 CD10 PT5 PT10 GFPT5 GFPT10 η 0.1 0.1 0.1 0.1 0.1 0.1 0.1 k 1 5 10 1 1 1 1 T - - - 20 20 20 20 M - - - 5 10 5 10 λ 0.1 0.1 batch 60 60 60 60 60 60 60 iter 1 000 1 000 1 000 1 000 1 000 1 000 1000 -
[1] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504-507 doi: 10.1126/science.1127647 [2] Le Roux N, Heess N, Shotton J, Winn J. Learning a generative model of images by factoring appearance and shape. Neural Computation, 2011, 23(3): 593-650 doi: 10.1162/NECO_a_00086 [3] Lee H, Grosse R, Ranganath R, Ng A Y. Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations. In: Proceedings of the 26th Annual International Conference on Machine Learning (ICML). Montreal, Canada: ACM, 2009. 609-616 [4] Bengio Y. Learning deep architectures for AI. Foundations and Trends in Machine Learning, 2009, 2(1): 1-127 doi: 10.1561/2200000006 [5] Deng L, Abdel-Hamid O, Yu D. A deep convolutional neural network using heterogeneous pooling for trading acoustic invariance with phonetic confusion. In: Proceedings of the 2013 International Conference on Acoustics, Speech and Signal Processing (ICASSP). Vancouver, BC, Canada: IEEE, 2013. DOI: 10.1109/ICASSP.2013.6638952 [6] Deng L. Design and learning of output representations for speech recognition. In: Proceedings of the 2013 Neural Information Processing Systems (NIPS) Workshop on Learning Output Representations. South Lake Tahoe, United States: NIPS, 2013. [7] Tan C C, Eswaran C. Reconstruction and recognition of face and digit images using autoencoders. Neural Computing and Application, 2010, 19(7): 1069-1079 doi: 10.1007/s00521-010-0378-4 [8] 郭潇逍, 李程, 梅俏竹.深度学习在游戏中的应用.自动化学报, 2016, 42(5): 676-684 http://www.aas.net.cn/CN/abstract/abstract18857.shtmlGuo Xiao-Xiao, Li Cheng, Mei Qiao-Zhu. Deep learning applied to games. Acta Automatica Sinica, 2016, 42(5): 676-684 http://www.aas.net.cn/CN/abstract/abstract18857.shtml [9] 田渊栋.阿法狗围棋系统的简要分析.自动化学报, 2016, 42(5): 671-675 http://www.aas.net.cn/CN/abstract/abstract18856.shtmlTian Yuan-Dong. A simple analysis of AlphaGo. Acta Automatica Sinica, 2016, 42(5): 671-675 http://www.aas.net.cn/CN/abstract/abstract18856.shtml [10] 段艳杰, 吕宜生, 张杰, 赵学亮, 王飞跃.深度学习在控制领域的研究现状与展望.自动化学报, 2016, 42(5): 643-654 http://www.aas.net.cn/CN/abstract/abstract18852.shtmlDuan Yan-Jie, Lv Yi-Sheng, Zhang Jie, Zhao Xue-Liang, Wang Fei-Yue. Deep learning for control: the state of the art and prospects. Acta Automatica Sinica, 2016, 42(5): 643-654 http://www.aas.net.cn/CN/abstract/abstract18852.shtml [11] 耿杰, 范剑超, 初佳兰, 王洪玉.基于深度协同稀疏编码网络的海洋浮筏SAR图像目标识别.自动化学报, 2016, 42(4): 593-604 http://www.aas.net.cn/CN/abstract/abstract18846.shtmlGeng Jie, Fan Jian-Chao, Chu Jia-Lan, Wang Hong-Yu. Research on marine floating raft aquaculture SAR image target recognition based on deep collaborative sparse coding network. Acta Automatica Sinica, 2016, 42(4): 593-604 http://www.aas.net.cn/CN/abstract/abstract18846.shtml [12] Deng L, Hinton G, Kingsbury B. New types of deep neural network learning for speech recognition and related applications: an overview. In: Proceedings of the 2013 International Conference on Acoustics, Speech and Signal Processing (ICASSP). Vancouver, BC, Canada: IEEE, 2013. DOI: 10.1109/ICASSP.2013.6639344 [13] Erhan D, Courville A C, Bengio Y, Vincent P. Why does unsupervised pre-training help deep learning? In: Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS). Sardinia, Italy: JMLR, 2010. 201-208 [14] Salakhutdinov R, Hinton G E. Deep Boltzmann machines. In: Proceedings of the 12th International Conference on Artificial Intelligence and Statistics (AISTATS). Florida, USA: JMLR, 2009. 448-455 [15] Swersky K, Chen B, Marlin B, De Freitas M. A tutorial on stochastic approximation algorithms for training restricted Boltzmann machines and deep belief nets. In: Proceedings of the 2010 Information Theory and Applications Workshop (ITA). La Jolla, California, USA: IEEE, 2010. 1-10 [16] Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets. Neural Computation, 2006, 18(7): 1527-1554 doi: 10.1162/neco.2006.18.7.1527 [17] Fischer A, Igel C. Bounding the bias of contrastive divergence learning. Neural Computation, 2011, 23(3): 664-673 doi: 10.1162/NECO_a_00085 [18] Tieleman T. Training restricted Boltzmann machines using approximations to the likelihood gradient. In: Proceedings of the 25th International Conference on Machine Learning (ICML). Helsinki, Finland: ACM, 2008. 1064-1071 [19] Tieleman T, Hinton G E. Using fast weights to improve persistent contrastive divergence. In: Proceedings of the 26th International Conference on Machine Learning (ICML). Montréal, Canada: ACM, 2009. 1033-1040 [20] Sutskever I, Tieleman T. On the convergence properties of contrastive divergence. In: Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS). Sardinia, Italy: JMLR, 2010. 789-795 [21] Fischer A, Igel C. Parallel tempering, importance sampling, and restricted Boltzmann machines. In: Proceedings of the 5th Workshop on Theory of Randomized Search Heuristics (ThRaSH). Copenhagen, Denmark: University of Copenhagen, 2011. 99-119 [22] Desjardins G, Courville A, Bengio Y. Adaptive parallel tempering for stochastic maximum likelihood learning of RBMs. In: Proceedings of NIPS 2010 Workshop on Deep Learning and Unsupervised Feature Learning. Whistler, Canada: Computer Science, 2010. arXiv: 1012.3476 [23] Cho K, Raiko T, Ilin A. Parallel tempering is efficient for learning restricted Boltzmann machines. In: Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN). Barcelona, Spain: IEEE, 2010. 3246-3253 [24] Brakel P, Dieleman S, Schrauwen B. Training restricted Boltzmann machines with multi-tempering: harnessing parallelization. In: Proceedings of the 22nd International Conference on Artificial Neural Networks. Berlin Heidelberg, Germany: Springer, 2012. 92-99 [25] Desjardins G, Courville A C, Bengio Y, Vincent P, Dellaleau O. Tempered Markov chain Monte Carlo for training of restricted Boltzmann machines. In: Proceedings of the 13th International Workshop on Artificial Intelligence and Statistics (AISTATS). Washington, DC, USA: IEEE, 2010. 45-152 [26] Fischer A, Igel C. Training restricted Boltzmann machines: an introduction. Pattern Recognition, 2014, 47(1): 25-39 doi: 10.1016/j.patcog.2013.05.025 [27] Bengio Y, Delalleau O. Justifying and generalizing contrastive divergence. Neural Computation, 2009, 21(6): 1601-1621 doi: 10.1162/neco.2008.11-07-647 -




 下载:
下载: