Operational Feedback Control of Industrial Processes in a Wireless Network Environment
-
摘要: 针对一类工业过程运行控制中采用无线网络传输运行指标反馈值时存在的噪声和丢包问题,建立了输入为过程控制的输入输出、输出为运行指标的随机过程模型;提出了由不同采样速率的过程控制与过程控制设定值反馈控制组成的运行反馈控制方法;采用Lyapunov函数和不同采样频率的提升技术设计了过程PI控制器参数和过程控制设定值反馈控制器参数,保证了双闭环控制系统的随机稳定性;同时实现了运行指标实际值与目标值稳态误差的均值为零;通过浮选过程运行反馈控制仿真实验验证了本文所提方法的有效性.Abstract: This paper studies operational control design for a class of industrial processes in which the operational index is transmitted back via wireless networks, whose noise and packet dropout may negatively affect the operational control performance. Firstly, a stochastic process model of operational index is established with the input and output of process control as its input and the operational index as its output. Secondly, a dual-layer model combining process control and set-point feedback control is presented with different sampling rates. Thirdly, a Lyapunov function and a lifting method between multirate systems are adopted to design a process PI controller and a set-point feedback controller to guarantee the stochastic stability of the dual closed-loop control system and that the mean value of steady-state error between the realistic and target operational index is zero. Finally, a simulation experiment on the operational feedback control in an industrial flotation process is conducted to demonstrate the effectiveness of the proposed method.
-
Key words:
- Operational index /
- wireless networks /
- noise /
- packet dropout /
- flotation processes
-
表 1 浮选过程符号表
Table 1 Flotation process symbol table
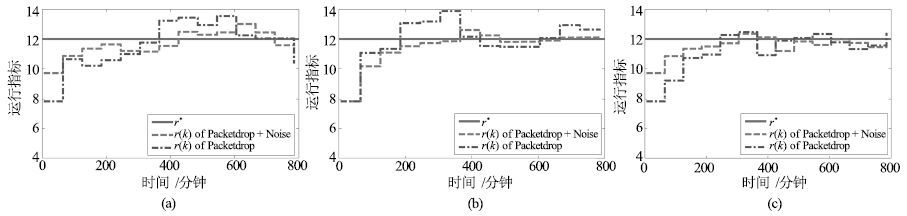
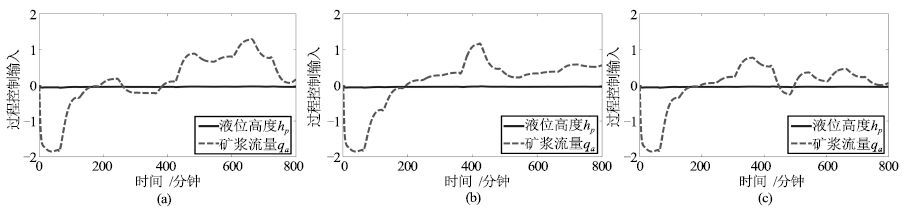
符号 物理含义 符号 物理含义 Mp 泥浆质量 hp 液位高度 Me 泡沫质量 qa 泥浆流量 Lcg 精矿品位 r* 运行指标目标值 Ltg 尾矿品位 r(T) 运行指标实际值 表 2 丢包与噪声序列表
Table 2 Packetdrop and noise table
采样点 1 2 3 4 5 6 7 8 9 10 11 12 13 δ(k)/a 0 0 1 0 0 0 1 1 1 1 1 0 1 δ(k)/b 0 1 1 1 1 1 1 1 1 0 1 0 1 δ(k)/c 0 1 1 0 1 0 0 1 0 0 0 1 0 ρ(k)/a -0.1256 0.0803 0.1931 0.1227 0.0814 -0.0060 -0.1542 0.0659 -0.0539 -0.1440 0.0267 0.1292 0.0696 ρ(k)/b -0.0197 -0.0351 0.1606 -0.1978 -0.0810 -0.1803 0.0773 0.0600 0.1932 0.0211 -0.0400 -0.1205 -0.0273 ρ(k)/c -0.1224 0.1619 0.0277 0.0527 -0.1062 0.0195 0.1726 -0.0659 0.0622 -0.0432 0.0509 0.0796 0.0214 -
[1] Cutler C R, Perry R T. Real time optimization with multivariable control is required to maximize profits. Computers and Chemical Engineering, 1983, 7(5):663-667 doi: 10.1016/0098-1354(83)80010-6 [2] 代伟, 柴天佑. 数据驱动的复杂磨矿过程运行优化控制方法. 自动化学报, 2014, 40(9):2005-2014 http://www.aas.net.cn/CN/abstract/abstract18472.shtmlDai Wei, Chai Tian-You. Data-driven optimal operational control of complex grinding processes. Acta Automatica Sinica, 2014, 40(9):2005-2014 http://www.aas.net.cn/CN/abstract/abstract18472.shtml [3] 柴天佑. 生产制造全流程优化控制对控制与优化理论方法的挑战. 自动化学报, 2009, 35(6):641-648 doi: 10.3724/SP.J.1004.2009.00641Chai Tian-You. Challenges of optimal control for plant-wide production processes in terms of control and optimization theories. Acta Automatica Sinica, 2009, 35(6):641-648 doi: 10.3724/SP.J.1004.2009.00641 [4] Chai T Y, Ding J L, Wu F H. Hybrid intelligent control for optimal operation of shaft furnace roasting process. Control Engineering Practice, 2011, 19(3):264-275 doi: 10.1016/j.conengprac.2010.05.002 [5] 柴天佑. 复杂工业过程运行优化与反馈控制. 自动化学报, 2013, 39(11):1744-1757 doi: 10.3724/SP.J.1004.2013.01744Chai Tian-You. Operational optimization and feedback control for complex industrial processes. Acta Automatica Sinica, 2013, 39(11):1744-1757 doi: 10.3724/SP.J.1004.2013.01744 [6] Pan Hong-Guang, Gao Hai-Nan, Sun Yao, Zhang Ying, Ding Bao-Cang. The algorithm and software implementation for double-layered model predictive control based on multi-priority rank steady-state optimization. Acta Automatica Sinica, 2014, 40(3):405-414(潘红光, 高海南, 孙耀, 张英, 丁宝苍. 基于多优先级稳态优化的双层结构预测控制算法及软件实现. 自动化学报, 2014, 40(3):405-414 http://cn.bing.com/academic/profile?id=2365970690&encoded=0&v=paper_preview&mkt=zh-cn [7] Findeisen W, Bailey F N, Bryds M, Malinawski K, Tatjewski P, Wozniak A. Control and Coordination in Hierarchical Systems. New York:John Wiley & Son, 1980. [8] 柴天佑, 丁进良, 王宏, 苏春翌. 复杂工业过程运行的混合智能优化控制方法. 自动化学报, 2008, 34(5):506-515 http://www.aas.net.cn/CN/abstract/abstract13476.shtmlChai Tian-You, Ding Jin-Liang, Wang Hong, Su Chun-Yi. Hybrid intelligent optimal control method for operation of complex industrial processes. Acta Automatica Sinica, 2008, 34(5):506-515 http://www.aas.net.cn/CN/abstract/abstract13476.shtml [9] 范家璐, 张也维, 柴天佑. 一类工业过程运行反馈优化控制方法. 自动化学报, 2015, 41(10):1754-1761 http://www.aas.net.cn/CN/abstract/abstract18749.shtmlFan Jia-Lu, Zhang Ye-Wei, Chai Tian-You. Optimal operational feedback control for a class of industrial processes. Acta Automatica Sinica, 2015, 41(10):1754-1761 http://www.aas.net.cn/CN/abstract/abstract18749.shtml [10] Chai T Y, Zhao L, Qiu J B, Liu F Z, Fan J L. Integrated network-based model predictive control for setpoints compensation in industrial processes. IEEE Transactions on Industrial Informatics, 2013, 9(1):417-426 doi: 10.1109/TII.2012.2217750 [11] Liu F Z, Gao H J, Qiu J B, Yin S, Fan J L, Chai T Y. Networked multirate output feedback control for setpoints compensation and its application to rougher flotation process. IEEE Transactions on Industrial Electronics, 2014, 61(1):460-468 doi: 10.1109/TIE.2013.2240640 [12] Wang T, Gao H J, Qiu J B. A combined adaptive neural network and nonlinear model predictive control for multirate networked industrial process control. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(2):416-425 doi: 10.1109/TNNLS.2015.2411671 [13] Jiang Y, Fan J L, Chai T Y, Chen T W. Setpoint dynamic compensation via output feedback control with network induced time delays. In:Proceedings of the 2015 American Control Conference. Chicago, IL:IEEE, 2015.5384-5389 [14] Perera C, Zaslavsky A, Christen P, Georgakopoulos D. Sensing as a service model for smart cities supported by internet of things. Transactions on Emerging Telecommunications Technologies, 2014, 25(1):81-93 doi: 10.1002/ett.2704 [15] Xu L D, He W, Li S C. Internet of things in industries:a survey. IEEE Transactions on Industrial Informatics, 2014, 10(4):2233-2243 doi: 10.1109/TII.2014.2300753 [16] Gungor V C, Hancke G P. Industrial wireless sensor networks:challenges, design principles, and technical approaches. IEEE Transactions on Industrial Electronics, 2009, 56(10):4258-4265 doi: 10.1109/TIE.2009.2015754 [17] Lu X, Zhang H S. Optimal estimation in wireless sensor networks with double measurements and multiplicative noise. In:Proceedings of the 29th Chinese Control Conference (CCC). Beijing, China:IEEE, 2010.4837-4840 [18] Boyd S, El Ghaoui L, Feron E, Balakrishnan V. Linear Matrix Inequalities in System and Control Theory. USA:Society for Industrial and Applied Mathematics, 1994. http://cn.bing.com/academic/profile?id=852963576&encoded=0&v=paper_preview&mkt=zh-cn [19] Khasminskii R. Stochastic Stability of Differential Equations. Springer-Verlag, 2012. http://cn.bing.com/academic/profile?id=2131404431&encoded=0&v=paper_preview&mkt=zh-cn [20] Harris C C. Multiphase models of flotation machine behaviour. International Journal of Mineral Processing, 1978, 5(2):107-129 doi: 10.1016/0301-7516(78)90009-1 [21] Thornton A J. The Application and Future Development of Adaptive Control to the Froth Flotation Process[Ph.D. dissertation], The University of Queensland, Australian, 2015. [22] Maldonado M, Sbarbaro D, Lizama E. Optimal control of a rougher flotation process based on dynamic programming. Minerals Engineering, 2007, 20(3):221-232 doi: 10.1016/j.mineng.2006.08.015 -





 下载:
下载: