基于多核多分类相关向量机的模拟电路故障诊断方法

高明哲; 许爱强; 唐小峰; 张伟

doi:10.16383/j.aas.2017.c160779

基于多核多分类相关向量机的模拟电路故障诊断方法

doi: 10.16383/j.aas.2017.c160779

高明哲^1, ,,
许爱强^2,,
唐小峰^2,,
张伟^2,

1.
中国人民解放军 91054部队北京 102442
2.
海军航空工程学院科研部烟台 264001

基金项目:

武器装备预研基金 020214JB14435

详细信息

作者简介:
许爱强  海军航空工程学院科研部教授.主要研究方向为电子信息系统的测试与故障诊断技术.E-mail:hy_xuaiqiang@163.com

唐小峰  海军航空工程学院科研部博士研究生.分别于2007年和2010年获得国防科技大学航天工程学士学位和武器系统与运用工程硕士学位.主要研究方向为电路的测试、故障建模和故障诊断.E-mail:vivorimage@126.com

张伟  海军航空工程学院科研部博士研究生.分别于2012年和2014年获得海军航空工程学院信息与通信工程学士学位和硕士学位.主要研究方向为核方法, 电子设备的智能故障诊断.E-mail:hjhy1989@163.com

通讯作者:
高明哲中国人民解放军91054部队工程师.分别于2011年、2013年和2017年获得海军航空工程学院信息与通信工程学士学位、硕士学位和博士学位.主要研究方向为模式识别, 电子设备的故障诊断与预测.本文通信作者.E-mail:mac7872@163.com

计量
- 文章访问数: 2893
- HTML全文浏览量: 691
- PDF下载量: 632
- 被引次数: 0
出版历程
- 收稿日期: 2016-11-23
- 录用日期: 2017-06-22
- 刊出日期: 2019-02-20

Analog Circuit Diagnostic Method Based on Multi-kernel Learning Multiclass Relevance Vector Machine

1.
The Chinese People's Liberation Army 91054 Unit, Beijing 102442
2.
Department of Scientific Research, Naval Aeronautical and Astronautical University, Yantai 264001

Funds:

Weaponry Pre-research Foundation 020214JB14435

More Information

Author Bio:
Professor in the Department of Scientific Research, Naval Aeronautical and Astronautical University. His research interest covers testing and diagnosis of electronic information system

Ph. D. candidate in the Department of Scientific Research, Naval Aeronautical and Astronautical University. He received his bachelor and master degrees in aerospace engineering and weapon systems and utilization engineering from National University of Defense Technology in 2007 and 2010, respectively. His research interest covers circuit test and diagnosis, fault modeling

Ph. D. candidate in the Department of Scientific Research, Naval Aeronautical and Astronautical University. He received his bachelor and master degrees in information and communication engineering from Naval Aeronautical and Astronautical University in 2012 and 2014, respectively. His research interest covers kernel methods, intelligent fault diagnosis of electronic equipment

Corresponding author: GAO Ming-Zhe Engineer at the Chinese People's Liberation Army 91054 Unit. He received his bachelor, master, and Ph. D. degrees in information and communication engineering from Naval Aeronautical and Astronautical University in 2011, 2013, and 2017, respectively. His research interest covers pattern recognition, fault diagnosis, and prediction of electronic equipment. Corresponding author of this paper

摘要

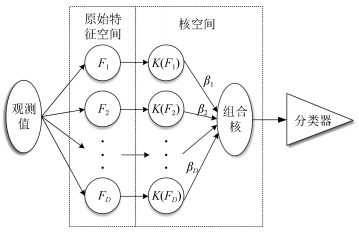
摘要: 针对模拟电路实际存在的多类故障问题，本文提出一种基于多核多分类相关向量机（Multi-kernel learning multiclass relevance vector machine，MKL-mRVM）的模拟电路故障诊断方法.所提方法能够在故障数据所在的原始特征空间上建立多个非线性核，在构建分类器的同时实现故障特征的约简；同时，基于贝叶斯框架的分类模型还能够给出诊断结果的后验概率.通过两个电路的诊断实验证明了所提方法的优越性和实用性.
- 故障诊断 /
- 模拟电路 /
- 相关向量机 /
- 特征约简 /
- 分类概率
Abstract: Aimed at the problem of multi-class fault diagnosis in practical analog circuits, a new diagnostic method based on multi-kernel learning multiclass relevance vector machine (MKL-mRVM) is proposed. The proposed method can build multi-kernels in the feature space where fault data are originally represented, which can realize the reduction of fault features during the modeling of classifier. In addition, the classifier based on Bayesian framework is able to output the posterior probability of diagnostic results. The fault diagnostic results of two circuits demonstrate the advantage and practicability of the proposed method.
- Fault diagnosis /
- analog circuit /
- relevance vector machine /
- feature reduction /
- classification probability
注释:

1) 本文责任编委钟麦英

HTML全文

图 1 多核组合原理图

Fig. 1 Combination of multi-kernels

下载: 全尺寸图片幻灯片

图 2 MKL-mRVM模型结构示意图

Fig. 2 Schematic diagram of MKL-mRVM

下载: 全尺寸图片幻灯片

图 3 诊断实施框架示意图

Fig. 3 Implementation framework of the diagnosis

下载: 全尺寸图片幻灯片

图 4 模糊度示意图

Fig. 4 Schematic diagram of ambiguity

下载: 全尺寸图片幻灯片

图 5 Sallen-Key带通滤波电路结构图

Fig. 5 Sallen-Key band-pass fllter circuit diagram

下载: 全尺寸图片幻灯片

图 6 几类故障的频率响应曲线

Fig. 6 Frequency response curves of faults

下载: 全尺寸图片幻灯片

图 7 MKL-mRVM的迭代过程

Fig. 7 Diagnostic performance comparison of 3 methods

下载: 全尺寸图片幻灯片

图 8 故障特征对应的加权系数值

Fig. 8 The weighting factors of fault features

下载: 全尺寸图片幻灯片

图 9 诊断结果的置信度

Fig. 9 Confldence of diagnostic results

下载: 全尺寸图片幻灯片

图 10 Biquad低通滤波电路结构图

Fig. 10 Biquad low-pass fllter circuit diagram

下载: 全尺寸图片幻灯片

图 11 几类故障的频率响应曲线

Fig. 11 Frequency response curves of faults

下载: 全尺寸图片幻灯片

图 12 不同门限下f0所在的模糊组

Fig. 12 Ambiguity groups of f0 under difierent thresholds

下载: 全尺寸图片幻灯片

表 1 变异操作

Table 1 Mutation operators

操作	名称	描述
PCH	参数改变(Parameter change)	将元件的指定参数偏离其容差范围
ROP	电阻开路(Resistive open)	在元件的端口间接入一个阻值极大的电阻以表示开路
LRB	局部电阻桥接(Local resistive bridging)	在同一元件的两个端口间接入一个阻值极小的电阻
GRB	全局电阻桥接(Global resistive bridging)	在不同元件的两个节点间接入一个阻值极小的电阻
NSP	节点分裂(Node splitting)	将一个节点分为两个, 并在分出的节点上接入一个阻值极大的电阻

下载: 导出CSV

表 2 Sallen-Key带通滤波电路故障描述

Table 2 Faults in Sallen-Key band-pass fllter

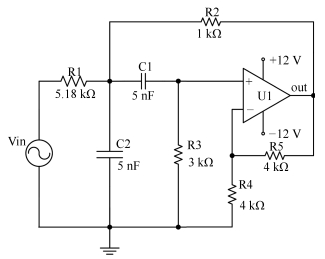
编号	故障描述	标称值	故障值
f0	无故障	—	—
f1	C1↑	5 nF	[6 ~ 10] nF
f2	C1↓	5 nF	[0.5 ~ 4] nF
f3	C2↑	5 nF	[6 ~ 10] nF
f4	C2↓	5 nF	[0.5 ~ 4] nF
f5	R1↑	5.18 k$\Omega$	[6.22 ~ 10.36] k$\Omega$
f6	R1↓	5.18 k$\Omega$	[0.52 ~ 4.14] k$\Omega$
f7	R2↑	1 k$\Omega$	[1.2 ~ 2] k$\Omega$
f8	R2↓	1 k$\Omega$	[0.1 ~ 0.8] k$\Omega$
f9	R3↑	2 k$\Omega$	[2.4 ~ 4] k$\Omega$
f10	R3↓	2 k$\Omega$	[0.2 ~ 1.6] k$\Omega$
f11	R4↑	4 k$\Omega$	[4.8 ~ 8] k$\Omega$
f12	R4↓	4 k$\Omega$	[0.4 ~ 3.2] k$\Omega$
f13	R5↑	4 k$\Omega$	[4.8 ~ 8] k$\Omega$
f14	R5↓	4 k$\Omega$	[0.4 ~ 3.2] k$\Omega$

下载: 导出CSV

表 3 三种方法的诊断性能对比

Table 3 Diagnostic performance comparison of 3 methods

方法	漏判率	误判率	检测率	隔离率	准确率	训练时间/s	测试时间/s
MKL-mRVM	0.0107	0.0200	0.9986	0.9893	0.9640	381.43	3.007E$-$04
OAO-SVM	0.0071	0.0600	0.9957	0.9928	0.9160	2.2103	1.781E$-$04
kELM	0.0114	0.0900	0.9935	0.9886	0.9020	0.1287	3.607E$-$05

下载: 导出CSV

表 4 Biquad低通滤波电路故障描述

Table 4 Faults in Biquad low-pass fllter

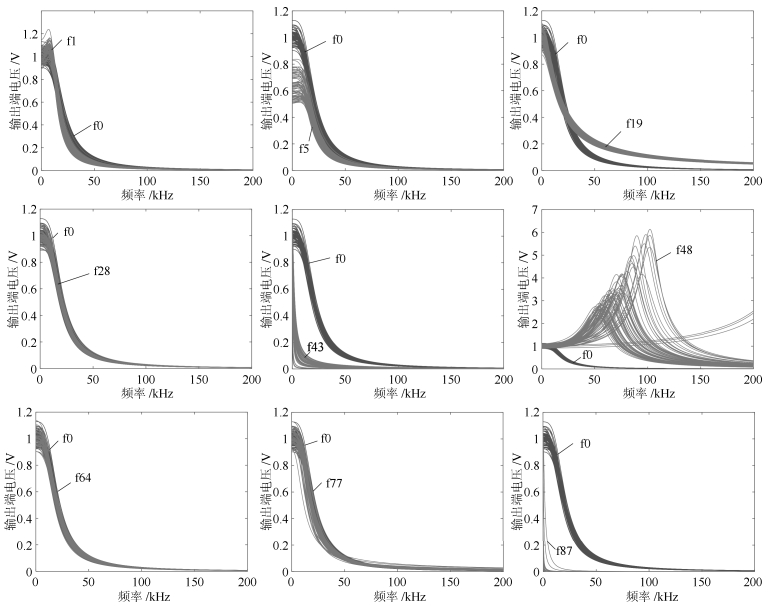
编号	故障描述	编号	故障描述	编号	故障描述	编号	故障描述
f0	无故障	f24	ROP (R4, +)	f48	LRB (R4, +, $-$)	f72	GRB (n2, in)
f1	PCH (C1↑)	f25	ROP (R5, +)	f49	LRB (R5, +, $-$)	f73	GRB (n2, n4)
f2	PCH (C1↓)	f26	ROP (R6, +)	f50	LRB (R6, +, $-$)	f74	GRB (n2, n5)
f3	PCH (C2↑)	f27	ROP (R7, +)	f51	LRB (R7, +, $-$)	f75	GRB (n2, out)
f4	PCH (C2↓)	f28	ROP (U1, 1)	f52	LRB (U1, 1, 2)	f76	GRB (n3, in)
f5	PCH (R1↑)	f29	ROP (U1, 2)	f53	LRB (U1, 2, 3)	f77	GRB (n3, n5)
f6	PCH (R1↓)	f30	ROP (U1, 3)	f54	LRB (U1, 3, 4)	f78	GRB (n3, out)
f7	PCH (R2↑)	f31	ROP (U1, 4)	f55	LRB (U1, 4, 5)	f79	GRB (n4, in)
f8	PCH (R2↓)	f32	ROP (U1, 5)	f56	LRB (U1, 5, 1)	f80	GRB (n4, out)
f9	PCH (R3↑)	f33	ROP (U2, 1)	f57	LRB (U2, 1, 2)	f81	GRB (n5, in)
f10	PCH (R3↓)	f34	ROP (U2, 2)	f58	LRB (U2, 2, 3)	f82	GRB (n6, in)
f11	PCH (R4↑)	f35	ROP (U2, 3)	f59	LRB (U2, 3, 4)	f83	GRB (n6, n3)
f12	PCH (R4↓)	f36	ROP (U2, 4)	f60	LRB (U2, 4, 5)	f84	GRB (n6, n5)
f13	PCH (R5↑)	f37	ROP (U2, 5)	f61	LRB (U2, 5, 1)	f85	GRB (n6, out)
f14	PCH (R5↓)	f38	ROP (U3, 1)	f62	LRB (U3, 1, 2)	f86	GRB (in, out)
f15	PCH (R6↑)	f39	ROP (U3, 2)	f63	LRB (U3, 2, 3)	f87	NSP (n1, [2, 3] [1, 4])
f16	PCH (R6↓)	f40	ROP (U3, 3)	f64	LRB (U3, 3, 4)	f88	NSP (n1, [2, 4] [1, 3])
f17	PCH (R7↑)	f41	ROP (U3, 4)	f65	LRB (U3, 4, 5)	f89	NSP (n1, [3, 4] [1, 2])
f18	PCH (R7↓)	f42	ROP (U3, 5)	f66	LRB (U3, 5, 1)	f90	NSP (n4, [2, 3] [1, 4])
f19	ROP (C1, +)	f43	LRB (C1, +, $-$)	f67	GRB (n1, 0)	f91	NSP (n4, [2, 4] [1, 3])
f20	ROP (C2, +)	f44	LRB (C2, +, $-$)	f68	GRB (n1, n3)	f92	NSP (n4, [3, 4] [1, 2])
f21	ROP (R1, +)	f45	LRB (R1, +, $-$)	f69	GRB (n1, n4)
f22	ROP (R2, +)	f46	LRB (R2, +, $-$)	f70	GRB (n1, n5)
f23	ROP (R3, +)	f47	LRB (R3, +, $-$)	f71	GRB (n2, 0)

下载: 导出CSV

表 5 三种方法的诊断性能对比

Table 5 Diagnostic performance comparison of 3 methods

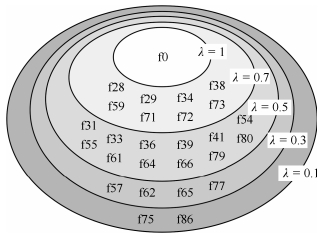
方法	$\lambda$	漏判率	误判率	检测率	隔离率	准确率	训练时间(s)	测试时间(s)
	1	0.0165	0.9200	0.9899	0.9834	0.6069
	0.7	0.0235	0.3400	0.9962	0.9765	0.7796
MKL-mRVM	0.5	0.0215	0.0600	0.9993	0.9893	0.8602	2.0436E$-$05	1.7472
	0.3	0.0132	0.0200	0.9997	0.9867	0.9202
	0.1	0.0132	0.0200	0.9997	0.9867	0.9406
	1	0.0254	0.9600	09894	0.9746	0.5303
	0.7	0.0608	0.4400	0.9950	0.9656	0.6905
OAO-SVM	0.5	0.0196	0.0400	0.9996	0.9804	0.8009	4.6002E$-$02	0.1628
	0.3	0.0167	0.0400	0.9996	0.9833	0.8598
	0.1	0.0167	0.0400	0.9996	0.9833	0.9191
	1	0.0402	0.9800	0.9890	0.9598	0.5006
	0.7	0.0437	0.4800	0.9941	0.9563	0.6301
kELM	0.5	0.0243	0.0800	0.9991	0.9757	0.7623	1.9524	1.4584E$-$04
	0.3	0.0191	0.0600	0.9996	0.9809	0.8271
	0.1	0.0191	0.0400	0.9996	0.9809	0.9013

下载: 导出CSV

表 6 其他特征的诊断性能

Table 6 Diagnostic performance of other features

故障特征	分类算法	训练时间(s)	分类准确率
高阶统计量	mRVM	6.1434E$-$03	0.2046
电路规格参数	mRVM	5.6213E$-$03	0.3871
MAF	mRVM	1.7324E$-$04	0.5113
MAF	MKL-mRVM	2.0436E$-$05	0.6069

下载: 导出CSV

参考文献(27)

[1]	Sarathi Vasan A S, Long B, Pecht M. Diagnostics and prognostics method for analog electronic circuits. IEEE Transactions on Industrial Electronics, 2013, 60(11):5277-5291 doi: 10.1109/TIE.2012.2224074
[2]	Ao Y C, Shi Y B, Zhang W, Li Y J. An approximate calculation of ratio of normal variables and its application in analog circuit fault diagnosis. Journal of Electronic Testing Theory & Applications, 2013, 29(4):555-565 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b9d32259512026ad9aacb8d8bfed98ac
[3]	Tadeusiewicz M, Halgas S. A new approach to multiple soft fault diagnosis of analog BJT and CMOS Circuits. IEEE Transactions on Instrumentation & Measurement, 2015, 64(10):2688-2695 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=24a338b94522b8a5d797fae90983bd1e
[4]	Tang X F, Xu A Q. Practical analog circuit diagnosis based on fault features with minimum ambiguities. Journal of Electronic Testing, 2016, 32(1):83-95 doi: 10.1007/s10836-015-5561-1
[5]	Liu Z B, Liu T M, Han J W, Bu S H, Tang X J, Pecht M. Signal Model-based fault coding for diagnostics and prognostics of analog electronic circuits. IEEE Transactions on Industrial Electronics, 2016, 64(1):605-614 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=64ef90618081629f53f3e48784a63595
[6]	Jing Y P, Yuan L F, He Y G. An analog circuit diagnosis method based on Adaptive-Kernel ICA. International Journal of Electronics and Electrical Engineering, 2016, 4(2):116-120
[7]	Luo H, Wang Y R, Lin H, Jiang Y Y. A new optimal test node selection method for analog circuit. Journal of Electronic Testing, 2012, 28(3):279-290 doi: 10.1007/s10836-011-5274-z
[8]	Tan H, Peng M F. Minimization of ambiguity in parametric fault diagnosis of analog circuits:a complex network approach. Applied Mathematics & Computation, 2012, 219(1):408-415 http://www.sciencedirect.com/science/article/pii/S0096300312006327
[9]	Kumar A, Singh A P. Fuzzy classifier for fault diagnosis in analog electronic circuits. ISA Transactions, 2013, 52(6):816-824 doi: 10.1016/j.isatra.2013.06.006
[10]	Litovski V, Andrejević M, Zwolinski M. Analogue electronic circuit diagnosis based on ANNs. Microelectronics Reliability, 2006, 46(8):1382-1391 doi: 10.1016/j.microrel.2005.11.008
[11]	Lin H J, Han J R, Zhang X H, Xu J B, Liu Y F. The research on fusion and diagnosis method of multi soft fault of nonlinear analog circuit. International Journal of U & E Service, Science and Technology, 2015, 8(11):191-198
[12]	Cui J, Wang Y R. A novel approach of analog circuit fault diagnosis using support vector machines classifier. Measurement, 2011, 44(1):281-289 doi: 10.1016/j.measurement.2010.10.004
[13]	Xie T, He Y G. Fault diagnosis of analog circuit based on high-order cumulants and information fusion. Journal of Electronic Testing, 2014, 30(5):505-514 doi: 10.1007/s10836-014-5478-0
[14]	Yuan L F, He Y G, Huang J Y, Sun Y C. A new neural-network-based fault diagnosis approach for analog circuits by using kurtosis and entropy as a preprocessor. IEEE Transactions on Instrumentation & Measurement, 2010, 59(3):586-595 http://ieeexplore.ieee.org/document/5256198
[15]	Kowalewski M. Two-center radial basis function network for classification of soft faults in electronic analog circuits. In:Proceedings of the Instrumentation and Measurement Technology Conference. Warsaw, Poland:IEEE, 2007. 1-6
[16]	Stratigopoulos H G, Mir S, Hora C, Kruseman B. Diagnosis of local spot defects in analog circuits. IEEE Transactions on Instrumentation & Measurement, 2012, 61(10):2701-2712 http://ieeexplore.ieee.org/document/6197714/
[17]	Zhang C L, He Y G, Yuan L F, He W, Xiang S, Li Z G. A novel approach for diagnosis of analog circuit fault by using GMKL-SVM and PSO. Journal of Electronic Testing, 2016, 32(5):531-540 doi: 10.1007/s10836-016-5616-y
[18]	Yu W X, Sui Y B, Wang J N. The faults diagnostic analysis for analog circuit based on FA-TM-ELM. Journal of Electronic Testing, 2016, 32(4):459-465 doi: 10.1007/s10836-016-5597-x
[19]	Han H, Wang H J, Tian S L, Zhang N. A new analog circuit fault diagnosis method based on improved mahalanobis distance. Journal of Electronic Testing, 2013, 29(1):95-102 doi: 10.1007/s10836-012-5342-z
[20]	徐丹蕾, 杜兰, 刘宏伟, 洪灵, 李彦兵.一种基于变分相关向量机的特征选择和分类结合方法.自动化学报, 2011, 37(8):932-943 http://www.aas.net.cn/CN/abstract/abstract17512.shtml Xu Dan-Lei, Du Lan, Liu Hong-Wei, Hong Ling, Li Yan-Bing. Joint feature selection and classification design based on variational relevance vector machine. Acta Automatica Sinica, 2011, 37(8):932-943 http://www.aas.net.cn/CN/abstract/abstract17512.shtml
[21]	Tipping M E. Sparse Bayesian learning and the relevance vector machine. Journal of Machine Learning Research, 2001, 1(3):211-244 http://d.old.wanfangdata.com.cn/Periodical/dsjs201802008
[22]	Psorakis I, Damoulas T, Girolami M A. Multiclass relevance vector machines:sparsity and accuracy. IEEE Transactions on Neural Networks, 2010, 21(10):1588-1598 doi: 10.1109/TNN.2010.2064787
[23]	Carin L, Dobeck G J. Relevance vector machine feature selection and classification for underwater targets. In:Proceedings of the OCEANS. San Diego, USA:IEEE, 2003. 1110-1110
[24]	Li D F, Hu W C. Feature selection with RVM and its application to prediction modeling. Lecture Notes in Computer Science. Berlin:Springer-Verlag, 2006. 1140-1144
[25]	Girolami M, Rogers S. Variational Bayesian multinomial probit regression with Gaussian process priors. Neural Computation, 2006, 18(8):1790-1817 doi: 10.1162/neco.2006.18.8.1790
[26]	Tipping M E, Faul A C. Fast marginal likelihood maximisation for sparse bayesian models. In:Proceedings of the 9th International Workshop on Artificial Intelligence and Statistics. Key West, Florida, USA:Miketipping, 2003. 3-6
[27]	Yang Z R. A fast algorithm for relevance vector machine. In:Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning. Burgos, Spain:Springer, 2006. 33-39