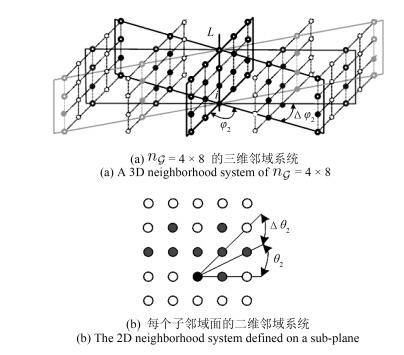
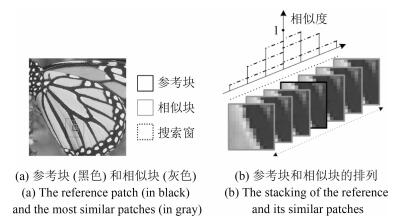
-
摘要: 要增强噪声图像的分辨率，传统的串联方式依次进行去噪与超分辨率重建两个步骤，但去噪算法去除噪声的同时也损失了部分细节信息，影响了后续超分辨率重建的质量.为了使低分辨率噪声图像中所有细节信息都能参与超分辨率重建，本文以非局部中心化稀疏表示（Nonlocally centralized sparse representation，NCSR）模型为基础，提出了基于自适应块组割（Patch-group-cuts，PGCuts）先验的噪声图像超分辨率重建方法，同时实现去噪和超分辨率重建功能.块组割先验基于新颖的三维邻域系统和块组模型，能够达到图像去噪、边缘平滑和边缘清晰等效果.重建时以边缘强度为参考对块组割先验进行自适应约束，由于块组割在平滑区域约束力较低，采用分区域融合的方式进一步抑制噪声.本文对合成的低分辨率噪声图像和真实的低分辨率噪声图像进行了重建实验，实验表明，基于自适应块组割先验的噪声图像超分辨率重建算法，在丰富细节的同时能抑制噪声的干扰，不但具有较高的峰值信噪比和结构相似度等客观评价值，而且在非光滑区域具有很好的主观重建效果.Abstract: To enhance resolution of a noisy image, the conventional method adopts a cascaded scheme of denoising followed by super-resolution (SR) reconstruction. However, the denoising algorithm inevitably causes some loss of high-frequency information in the image, especially in non-smooth regions, which significantly influences the quality of the subsequent SR reconstruction. To incorporate all the high-frequency information from the noisy low-resolution (LR) images into the SR reconstruction, a noisy image SR method with adaptive patch-group-cuts (PGCuts) prior is proposed, based on the nonlocally centralized sparse representation (NCSR) model. The proposed method performs denoising and SR reconstruction simultaneously. The PGCuts prior, which is built on a novel 3D neighborhood system and a patch-group model, is able to denoise the image, restore smooth and sharp edges, etc. The edge strength measurement is introduced to adaptively balance the constraint strength of PGCuts prior in reconstruction. As PGCuts constraint is weak in smooth regions, a region-based fusion scheme is also used to further suppress the noise. Reconstruction experiments are conducted on both synthesized and real noisy LR images. It is demonstrated that the proposed method can restore plenty of details in reconstructed SR images while still suppress the noise, giving not only high scores in objective criteria like PSNR and SSIM, but also very good visual effects in non-smooth regions in subjective evaluations.1) 本文责任编委 黄庆明
-
图 1 图像Butterfly高分辨率去噪图像能量损失图及边缘强度图
Fig. 1 The energy loss map and the edge strength map of the denoised HR image for image Butterfly
图 5 不同噪声标准差的PSNR均值和SSIM均值
Fig. 5 The average PSNR/SSIM values versus noise standard deviation for all the test images
图 6 噪声图像Church超分辨率结果比较(括号内的数字分别表示PSNR和SSIM)
Fig. 6 SR results of noisy LR image Church (PSNR and SSIM values are shown in bracket)
图 7 噪声图像Butterfly超分辨率结果比较(括号内的数字分别表示PSNR和SSIM)
Fig. 7 SR results of noisy LR image Butterfly (PSNR and SSIM values are shown in bracket)
图 9 噪声图像超分辨率重建的性能与运行时间综合比较图$\left(\sigma=20, o=2\right)$
Fig. 9 PSNR versus running time for different SR methods on noisy LR images $\left(\sigma=20, o=2\right)$
表 1 噪声图像超分辨率重建结果比较(PSNR (dB))
Table 1 PSNR (dB) comparison of different SR methods on noisy LR images
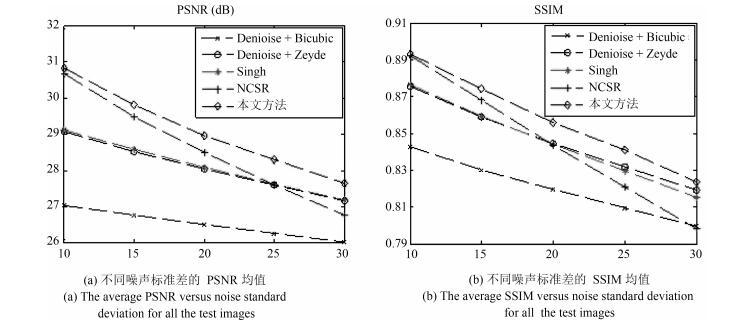
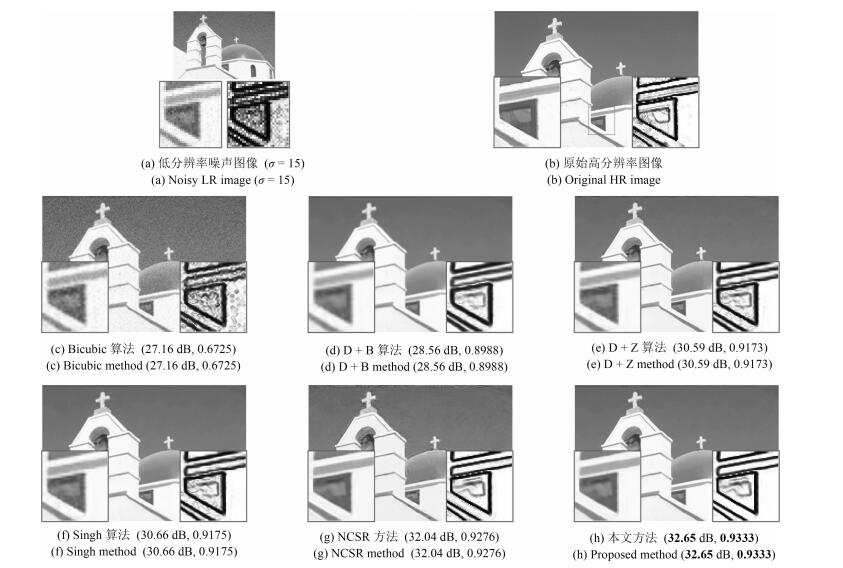
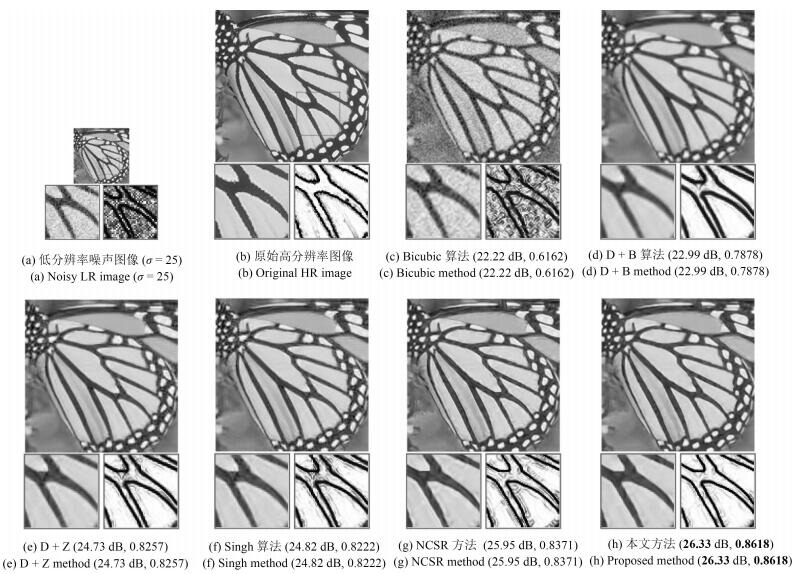
标准差 算法 Sail Woman Racing Bridge Man Church Butterfly Lena Ppt Status Average 15 Bicubic 28.36 27.43 25.17 25.32 25.18 27.16 23.29 27.48 23.27 25.76 25.84 D + B 30.61 28.94 25.77 25.86 25.53 28.56 23.47 28.88 23.66 26.28 26.76 D + Z 31.50 30.78 27.03 27.10 27.73 30.59 25.72 30.18 25.90 28.71 28.52 Singh 31.58 30.82 27.05 27.14 27.89 30.66 25.81 30.24 25.91 28.71 28.58 NCSR 31.64 31.58 27.50 27.61 29.42 32.04 27.75 30.42 27.52 29.46 29.49 Proposed 32.01 31.83 27.78 27.74 29.52 32.65 27.90 30.64 28.43 29.63 29.81 20 Bicubic 26.89 26.26 24.43 24.59 24.50 26.13 22.78 26.28 22.85 24.97 24.97 D + B 30.32 28.67 25.55 25.61 25.19 28.38 23.23 28.57 23.54 25.94 26.50 D + Z 31.03 30.27 26.65 26.69 27.04 30.23 25.21 29.65 25.64 27.97 28.04 Singh 31.10 30.30 26.67 26.73 27.21 30.30 25.30 29.68 25.65 27.90 28.08 NCSR 30.81 30.62 26.83 26.92 28.20 30.84 26.78 29.21 26.38 28.28 28.49 Proposed 31.12 30.98 27.13 27.17 28.41 31.85 27.01 29.72 27.67 28.51 28.96 25 Bicubic 25.53 25.14 23.63 23.81 23.79 25.08 22.22 25.13 22.36 24.15 24.08 D + B 30.04 28.40 25.34 25.39 24.85 28.19 22.99 28.28 23.40 25.60 26.25 D + Z 30.62 29.81 26.31 26.33 26.39 29.87 24.73 29.18 25.36 27.31 27.59 Singh 30.64 29.83 26.31 26.37 26.58 29.92 24.82 29.19 25.37 27.20 27.62 NCSR 29.71 29.77 26.20 26.28 27.05 29.78 25.95 28.29 25.48 27.35 27.59 Proposed 30.72 30.34 26.63 26.72 27.47 31.00 26.33 29.11 26.80 27.90 28.30 
下载: 导出CSV
表 2 噪声图像超分辨率重建结果比较(SSIM)
Table 2 SSIM comparison of different SR methods on noisy LR images
标准差 算法 Sail Woman Racing Bridge Man Church Butterfly Lena Ppt Status Average 15 Bicubic 0.6101 0.6587 0.6102 0.6277 0.7203 0.6725 0.7225 0.6523 0.8180 0.7716 0.6864 D + B 0.8475 0.8536 0.7028 0.7332 0.8572 0.8988 0.8122 0.8075 0.9380 0.8519 0.8303 D + Z 0.8648 0.8728 0.7347 0.7704 0.8895 0.9173 0.8577 0.8297 0.9654 0.8870 0.8589 Singh 0.8669 0.8729 0.7356 0.7724 0.8903 0.9175 0.8572 0.8300 0.9655 0.8838 0.8592 NCSR 0.8653 0.8764 0.7448 0.7844 0.9083 0.9276 0.8898 0.8183 0.9742 0.8915 0.8681 Proposed 0.8731 0.8816 0.7496 0.7867 0.9156 0.9333 0.8986 0.8311 0.9771 0.8975 0.8744 20 Bicubic 0.5054 0.5656 0.5402 0.5584 0.6510 0.5781 0.6661 0.5659 0.7556 0.7138 0.6100 D + B 0.8380 0.8449 0.6885 0.7179 0.8437 0.8948 0.7999 0.7951 0.9325 0.8393 0.8195 D + Z 0.8515 0.8616 0.7165 0.7499 0.8717 0.9116 0.8415 0.8132 0.9590 0.8697 0.8446 Singh 0.8522 0.8612 0.7171 0.7524 0.8718 0.9111 0.8393 0.8115 0.9590 0.8634 0.8439 NCSR 0.8395 0.8590 0.7198 0.7567 0.8836 0.9144 0.8629 0.7743 0.9642 0.8637 0.8438 Proposed 0.8558 0.8680 0.7285 0.7650 0.8936 0.9253 0.8785 0.8014 0.9690 0.8742 0.8559 25 Bicubic 0.4197 0.4884 0.4774 0.4963 0.5917 0.4994 0.6162 0.4916 0.6973 0.6595 0.5437 D + B 0.8294 0.8371 0.6767 0.7050 0.8304 0.8906 0.7878 0.7843 0.9262 0.8266 0.8094 D + Z 0.8397 0.8519 0.7011 0.7330 0.8543 0.9053 0.8257 0.7994 0.9520 0.8542 0.8317 Singh 0.8364 0.8507 0.7012 0.7354 0.8540 0.9034 0.8222 0.7957 0.9519 0.8451 0.8296 NCSR 0.8118 0.8423 0.6969 0.7318 0.8576 0.9002 0.8371 0.7387 0.9536 0.8379 0.8208 Proposed 0.8416 0.8577 0.7113 0.7463 0.8745 0.9156 0.8618 0.7837 0.9595 0.8598 0.8412
下载: 导出CSV
表 3 重建高分辨率图像SCM值比较$\left(\sigma=20\right)$
Table 3 SCM comparison of the reconstructed HR image$\left(\sigma=20\right)$
算法 Sail Woman Racing Bridge Man Church Butterfly Lena Ppt Status NCSR 1.35 1.92 2.62 2.51 4.08 2.00 5.96 2.46 3.50 5.24 Proposed 1.09 1.71 2.27 2.22 3.80 1.79 5.46 2.08 3.19 4.94
下载: 导出CSV
表 4 噪声图像超分辨率重建运行时间(s)比较$\left(\sigma=20\right)$
Table 4 Comparison of the running time (s) of different SR methods on noisy LR images $\left(\sigma=20\right)$
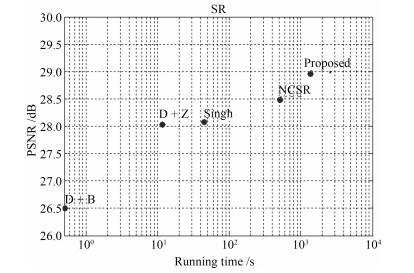
图像 放大因子/尺寸 D+B D+Z Singh NCSR Proposed Man 2/320x480 0.5 1.3×10 0.5×102 0.6×103 1.4×103 3/480×720 0.5 2.5×10 1.0×102 1.6×103 3.4×103 4/640×960 0.5 6.4×10 2.1×102 2.9×103 6.1×103 Butterfly 2/256×256 0.2 0.5×10 0.2×102 0.2×103 0.5×103 3/384×384 0.2 1.0×10 0.4×102 0.5×103 1.3×103 4/512×512 0.2 2.7×10 0.9×102 0.8×103 2.2×103 Ppt 2/656×528 1.2 2.7×10 1.1×102 1.4×103 3.5×103 3/984×792 1.2 5.5×10 2.1×102 3.8×103 8.4×103 4/1312×1056 1.2 14.7×10 4.8×102 4.9×103 14.6×103 Status 2/170×138 0.05 0.2×10 0.08×102 0.05×103 0.2×103 3/255×207 0.05 0.4×10 0.13×102 0.16×103 0.5×103 4/340×276 0.05 0.9×10 0.3×102 0.23×103 0.8×103
下载: 导出CSV
-
[1] Li Y P, Huttenlocher D P. Sparse long-range random field and its application to image denoising. In: Proceeding of the 10th European Conference on Computer Vision. Marseille, France: Springer, 2008. 344-357 [2] Roth S, Black M J. Fields of experts: a framework for learning image priors. In: Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, USA: IEEE, 2005. 860-867 [3] Tappen M F. Utilizing variational optimization to learn Markov random fields. In: Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, USA: IEEE, 2007. 1-8 [4] Nasri M, Nezamabadi-pour H. Image denoising in the wavelet domain using a new adaptive thresholding function. Neurocomputing, 2009, 72(4): 1012-1025 https://www.researchgate.net/publication/220549893_Image_denoising_in_the_wavelet_domain_using_a_new_adaptive_thresholding_function [5] Mihcak M K, Kozintsev I, Ramchandran K, Moulin P. Low-complexity image denoising based on statistical modeling of wavelet coefficients. IEEE Signal Processing Letters, 1999, 6(12): 300-303 doi: 10.1109/97.803428 [6] Buades A, Coll B, Morel J-M. A non-local algorithm for image denoising. In: Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, USA: IEEE, 2005. 60-65 [7] Dabov K, Foi A, Katkovnik V, Egiazarian K. Color image denoising via sparse 3D collaborative filtering with grouping constraint in luminance-chrominance space. In: Proceedings of the 2007 IEEE International Conference on Image Processing. San Antonio, USA: IEEE, 2007. I-313-I-316 [8] Dabov K, Foi A, Katkovnik V, Egiazarian K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095 doi: 10.1109/TIP.2007.901238 [9] 张瑞, 冯象初, 王斯琪, 常莉红.基于稀疏梯度场的非局部图像去噪算法.自动化学报, 2015, 41(9): 1542-1552 http://www.aas.net.cn/CN/abstract/abstract18729.shtmlZhang Rui, Feng Xiang-Chu, Wang Si-Qi, Chang Li-Hong. A sparse gradients field based image denoising algorithm via non-local means. Acta Automatica Sinica, 2015, 41(9): 1542-1552 http://www.aas.net.cn/CN/abstract/abstract18729.shtml [10] Zhang X J, Wu X L. Image interpolation by adaptive 2-D autoregressive modeling and soft-decision estimation. IEEE Transactions on Image Processing, 2008, 17(6): 887-896 doi: 10.1109/TIP.2008.924279 [11] Hung K-W, Siu W-C. Fast image interpolation using the bilateral filter. IET Image Processing, 2012, 6(7): 877-890 doi: 10.1049/iet-ipr.2011.0050 [12] Zhang K B, Gao X B, Tao D C, Li X L. Single image super-resolution with non-local means and steering kernel regression. IEEE Transactions on Image Processing, 2012, 21(11): 4544-4556 doi: 10.1109/TIP.2012.2208977 [13] Yan Q, Xu Y, Yang X K, Nguyen T Q. Single image superresolution based on gradient profile sharpness. IEEE Transactions on Image Processing, 2015, 24(10): 3187-3202 doi: 10.1109/TIP.2015.2414877 [14] Dai S Y, Han M, Xu W, Wu Y, Gong Y H, Katsaggelos A K. Softcuts: a soft edge smoothness prior for color image super-resolution. IEEE Transactions on Image Processing, 2009, 18(5): 969-981 doi: 10.1109/TIP.2009.2012908 [15] Zeyde R, Elad M, Protter M. On single image scale-up using sparse-representations. In: Proceedings of the 7th International Conference on Curves and Surfaces. Avignon, France: Springer, 2012. 711-730 [16] Peleg T, Elad M. A statistical prediction model based on sparse representations for single image super-resolution. IEEE Transactions on Image Processing, 2014, 23(6): 2569-2582 doi: 10.1109/TIP.2014.2305844 [17] Jia K, Wang X G, Tang X O. Image transformation based on learning dictionaries across image spaces. IEEE transactions on Pattern Analysis and Machine Intelligence, 2013, 35(2): 367-380 doi: 10.1109/TPAMI.2012.95 [18] 李民, 程建, 乐翔, 李小文.基于联合稀疏近似的彩色图像超分辨率重建.光电子·激光, 2011, 22(8): 1241-1245 http://www.cnki.com.cn/Article/CJFDTOTAL-GDZJ201108028.htmLi Min, Cheng Jian, Le Xiang, Li Xiao-Wen. Super-resolution reconstruction for color images based on simultaneous sparse approximation. Journal of Optoelectronics · Laser, 2011, 22(8): 1241-1245 http://www.cnki.com.cn/Article/CJFDTOTAL-GDZJ201108028.htm [19] Singh A, Porikli F, Ahuja N. Super-resolving noisy images. In: Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus, USA: IEEE, 2014. 2846-2853 [20] Dong W S, Zhang L, Shi G M, Li X. Nonlocally centralized sparse representation for image restoration. IEEE Transactions on Image Processing, 2013, 22(4): 1620-1630 doi: 10.1109/TIP.2012.2235847 [21] Zhang Y Q, Liu J Y, Yang W H, Guo Z M. Image super-resolution based on structure-modulated sparse representation. IEEE Transactions on Image Processing, 2015, 24(9): 2797-2810 doi: 10.1109/TIP.2015.2431435 [22] Li T, He X H, Teng Q Z, Wang Z Y, Ren C. Space-time super-resolution with patch group cuts prior. Signal Processing: Image Communication, 2015, 30: 147-165 doi: 10.1016/j.image.2014.10.007 [23] Boykov Y, Kolmogorov V. Computing geodesics and minimal surfaces via graph cuts. In: Proceedings of the 2003 IEEE International Conference on Computer Vision. Nice, France: IEEE, 2003. 26-33 [24] Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(11): 1222-1239 doi: 10.1109/34.969114 [25] Candés E J, Wakin M B, Boyd S P. Enhancing sparsity by reweighted l1 minimization. Journal of Fourier Analysis and Applications, 2008, 14(5-6): 877-905 doi: 10.1007/s00041-008-9045-x [26] 韩雨, 王卫卫, 冯象初.基于迭代重加权的非刚性图像配准.自动化学报, 2011, 37(9): 1059-1066 http://www.aas.net.cn/CN/abstract/abstract17529.shtmlHan Yu, Wang Wei-Wei, Feng Xiang-Chu. Iteratively reweighted method based nonrigid image registration. Acta Automatica Sinica, 2011, 37(9): 1059-1066 http://www.aas.net.cn/CN/abstract/abstract17529.shtml [27] Daubechies I, Defrise M, De Mol C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413-1457 doi: 10.1002/(ISSN)1097-0312 [28] 范文茹, 王化祥, 郝魁红.基于两步迭代TV正则化的电阻抗图像重建算法.仪器仪表学报, 2012, 33(3): 625-630 http://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201203021.htmFan Wen-Ru, Wang Hua-Xiang, Hao Kui-Hong. Two-step iterative TV regularization algorithm for image reconstruction of electrical impedance tomography. Chinese Journal of Scientific Instrument, 2012, 33(3): 625-630 http://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201203021.htm [29] Irani M, Peleg S. Motion analysis for image enhancement: resolution, occlusion, and transparency. Journal of Visual Communication and Image Representation, 1993, 4(4): 324-335 doi: 10.1006/jvci.1993.1030 [30] Dai S Y, Han M, Xu W, Wu Y, Gong Y H. Soft edge smoothness prior for alpha channel super resolution. In: Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, USA: IEEE, 2007. -
图(9) / 表(4)
计量
- 文章访问数: 2305
- HTML全文浏览量: 240
- PDF下载量: 737
- 被引次数: 0
