Nonlinear Subspace Modeling of Multivariate Molten Iron Quality in Blast Furnace Ironmaking and Its Application
-
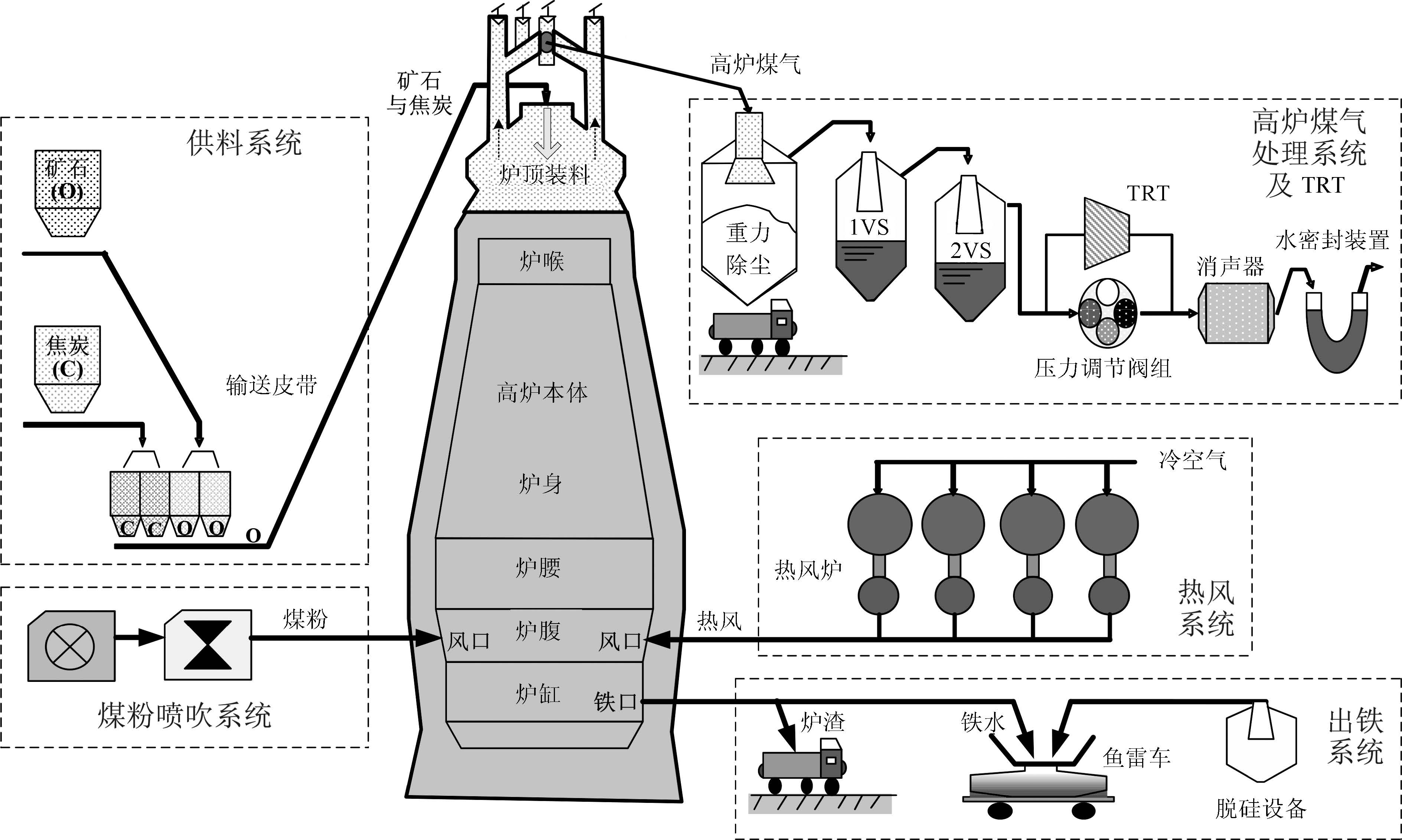
摘要: 高炉炼铁是一个物理化学反应复杂、多相多场耦合的大滞后、非线性动态系统，其关键工艺指标——铁水质量参数的检测、建模和控制一直是冶金工程和自动控制领域的难题.本文提出一种面向控制的数据驱动高炉炼铁多元铁水质量非线性子空间建模方法.首先，为了提高建模效率和降低计算复杂度，采用数据驱动典型相关性分析与相关性分析相结合的方法提取与铁水质量相关性最强的关键可控变量作为建模的输入变量；同时，为了更好地反映高炉非线性动态特性，将相关输入输出变量的时序和时滞关系在建模过程进行考虑；最后，采用基于最小二乘支持向量机（Least square support vector machine，LS-SVM）的非线性Hammerstein系统子空间辨识方法建立数据驱动的多元铁水质量非线性状态空间模型.同时，将核函数表示的模型非线性特性用多项式函数拟合，在仅损失很小模型精度的前提下大大降低模型的计算复杂度.基于实际数据的工业试验验证了所提建模方法的准确性、有效性和先进性.Abstract: Blast furnace ironmaking is a nonlinear dynamic process containing complex physical-chemical reaction, multi-phase multi-field coupling and large time delay. Measuring, modeling and control of the key process indices of ironmaking process, molten iron quality (MIQ) parameters, have always been treated as a difficult problem in metallurgic engineering and automation field. This paper presents a control oriented data-driven nonlinear subspace modeling method for multivariate prediction of MIQ. First, to improve modeling efficiency, data driven canonical correlation analysis (CCA) and correlation analysis (CA) are combined to pick out the most influential controllable variables from multitudinous factors to serve as the input variables of modeling. Second, to better reflect the nonlinear dynamic characteristics of blast furnace ironmaking process, the time series and time delays of the relevant input and output variables are taken into account. Finally, a data-driven nonlinear state-space model of MIQ is built using least square support vector machine (LS-SVM) based nonlinear subspace identification method for Hammerstein system. With polynomial fitting method, the nonlinear parts expressed by kernel functions in the obtained Hammerstein model are simplified, so as to greatly reduce the computational complexity of the model on the premise of only a small loss of accuracy. Industrial experiments based on real data verifies the accuracy, effectiveness and advancement of the proposed method.
-
图 2 多元铁水质量参数非线性子空间建模策略
Fig. 2 Strategy diagram of multivariable nonlinear dynamic modeling for molten iron quality
图 4 基于非线性子空间辨识的多元铁水质量模型在多项式拟合非线性特性前后的建模结果
Fig. 4 Modeling results of molten iron quality prediction with and without polynomial ¯tting
图 5 模型在多项式拟合非线性特性前后对多元铁水质量参数的实际估计效果
Fig. 5 Estimation results of molten iron quality prediction with and without polynomial ¯tting
图 6 不同建模方法对多元铁水质量的实际估计效果对比
Fig. 6 Estimation results of molten iron quality prediction with di®erent models
图 7 不同模型估计误差自相关函数
Fig. 7 Autocorrelation function of estimating error of di®erent models
图 8 不同建模方法的估计值与实际值散点图
Fig. 8 Scatter diagram of estimated and actual value by di®erent models
图 10 多元铁水质量预测控制控制量曲线
Fig. 10 Control input curves of predictive control of molten iron quality parameters
表 1 典型相关分析结果
Table 1 The results of canonical correlation analysis
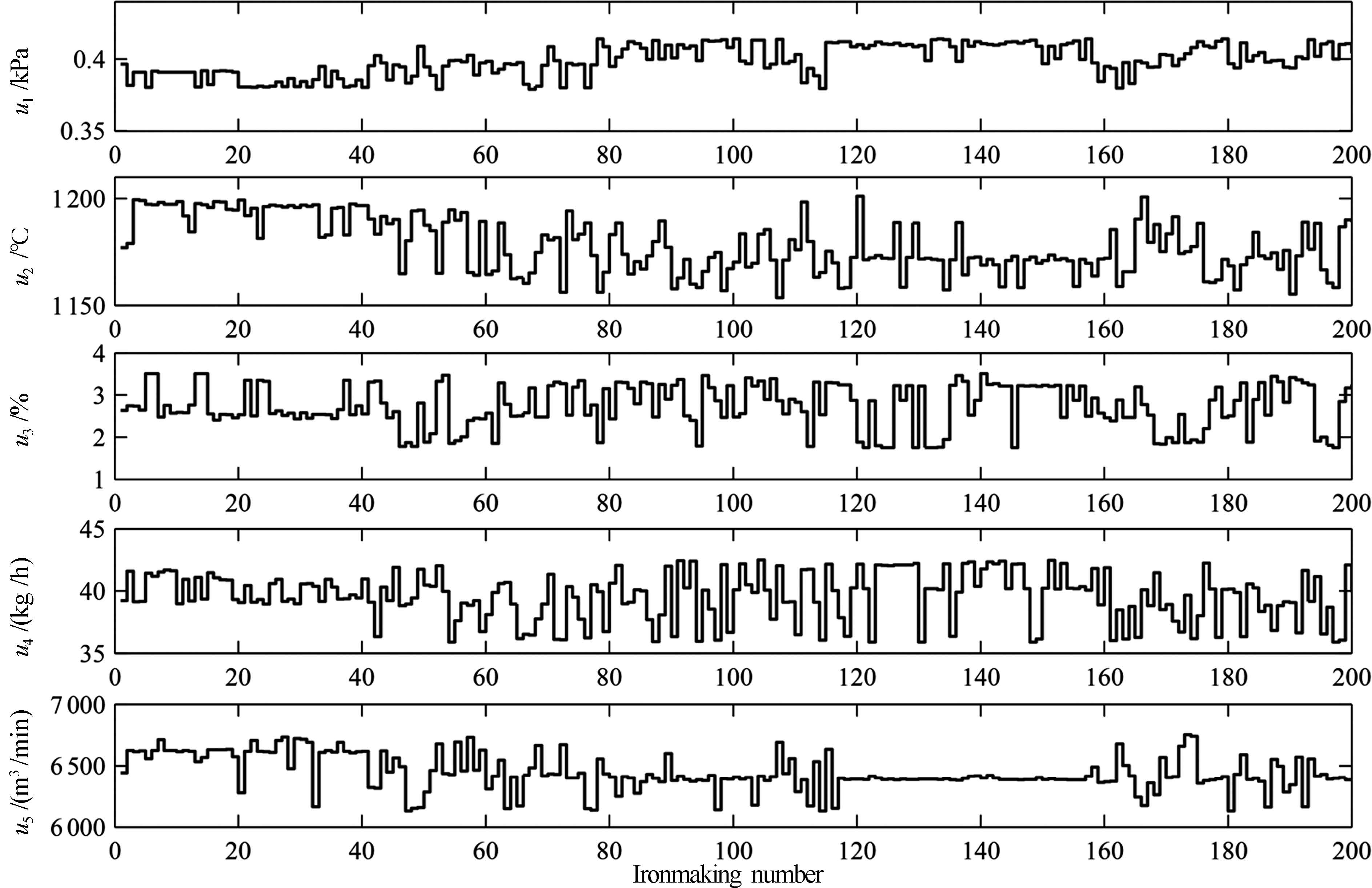
0.563[Si]-0.453[P]- 0.638[Si]+0.899[P]- -0.857[Si]-0.368[P]- 0.447[S]+0.287MIT 0.986[S]-0.518MIT 0.801[S]-0.398MIT 送风比 -1.103 -3.254 0.716 热风压力 0.587 -1.109 -1.493 顶压0 .974 -0.911 -0.320 压差 0.495 -7.118 2.506 顶压风量 -0.948 -0.794 3.185 透气性- 2.687 -4.104 -2.782 阻力系数 -2.702 6.501 -5.392 热风温度 -5.375 14.185 4.230 富氧流量 4.914 -4.014 -0.054 富氧率 -7.284 8.123 -0.377 设定喷煤量 0.998 -7.335 -3.443 鼓风湿度 0.096 0.208 -0.071 理论燃烧温度 3.789 -12.762 -5.639 标准风速 -0.439 -3.953 -0.717 实际风速 1.816 2.624 3.444 鼓风动能 -0.438 -4.662 -2.728 炉腹煤气量 -1.306 14.932 4.029 炉腹煤气指数 -0.176 -1.503 -0.335 
下载: 导出CSV
表 2 两种模型对各个铁水质量指标估计的均方根误差和计算时间比较
Table 2 Comparison between two models in RMSE for molten iron quality prediction and computation time
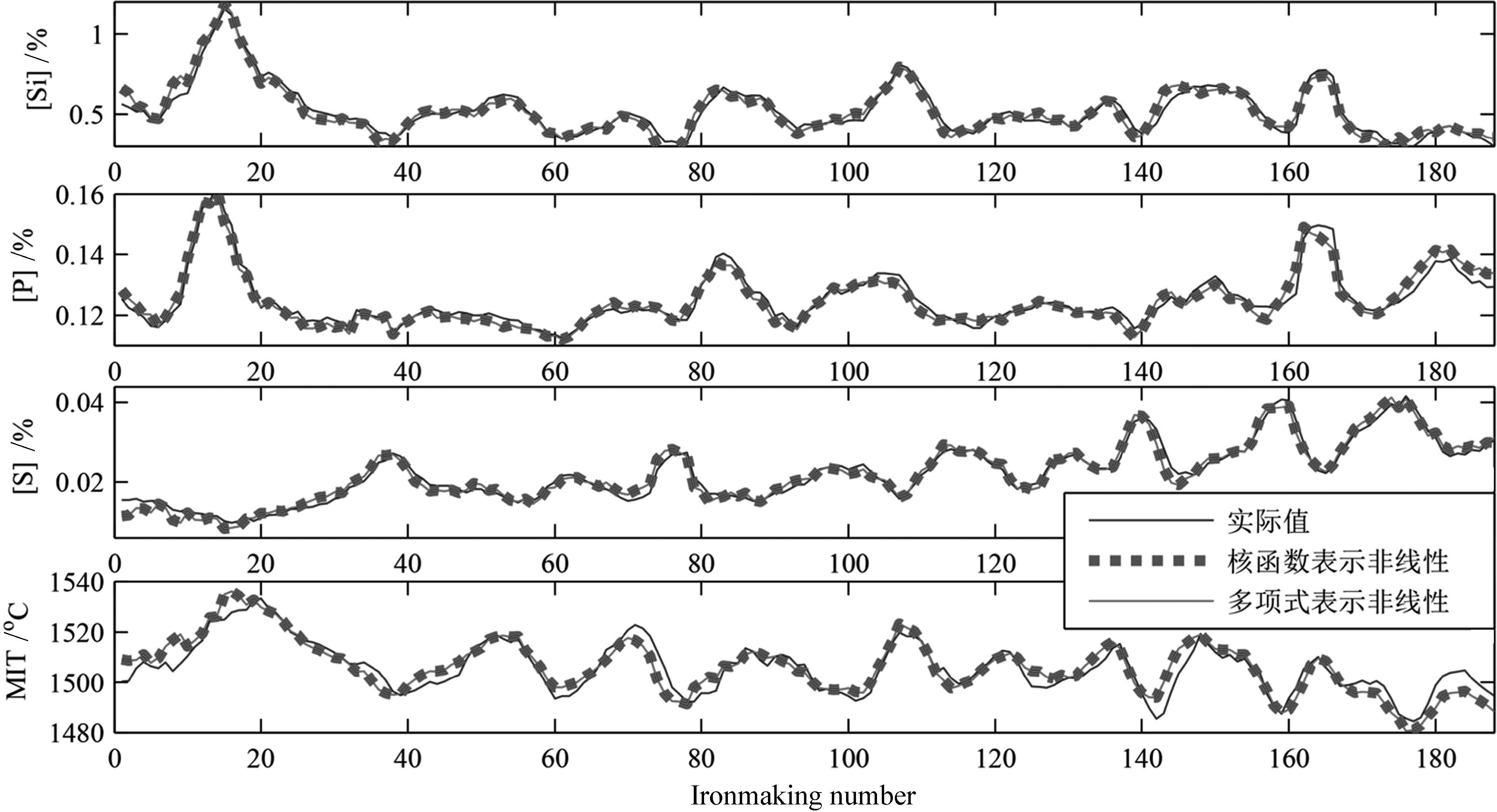
RMSE Time (s) [Si] (%) [P] (%) [S] (%) MIT (±C) Kernel 0.0633 0.0032 0.0021 6.2388 0.01123 Polynomial 0.0664 0.0031 0.0022 6.6907 0.00061
下载: 导出CSV
表 3 多元铁水质量估计值均方根误差比较
Table 3 RMSE for molten iron quality prediction
RMSE [Si] (%) [P] (%) [S] (%) MIT (±C) N-SM 0.0664 0.0031 0.0022 6.6907 L-SM 0.1584 0.0107 0.0073 8.4801 M-LS-SVR 0.0811 0.0058 0.0051 8.0037 RLS-ARMA 0.0721 0.0060 0.0044 7.2992
下载: 导出CSV
-
[1] Gao C H, Jian L, Luo S H. Modeling of the thermal state change of blast furnace hearth with support vector machines. IEEE Transaction on Industrial Electronics, 2012, 59(2): 1134-1145 doi: 10.1109/TIE.2011.2159693 [2] Kuang S B, Li Z Y, Yan D L, Qi Y H, Yu A B. Numerical study of hot charge operation in ironmaking blast furnace. Minerals Engineering, 2014, 63: 45-56 doi: 10.1016/j.mineng.2013.11.002 [3] östermark R, Saxén H. VARMAX-modelling of blast furnace process variables. European Journal of Operational Research, 1996, 90(1): 85-101 http://www.baidu.com/link?url=Q0cLAVW_Xt09DHbqwNsllCI9IBTcvPJeDS8qQcsDYrZuyiB2_aCBxPPJLH3kgDoecHrQCeXJCd6l8cE2Bfyt7p2Po-8xlSIaK-XLH732DFZzqIPkKripLUbVKXUsFvuLt1xU9-y_jNS2Z6iVSTWWOkZyXkrGmgMqM3TEBrnGCcEgZuD40Yw-Io0WSf9GaaPGJ2tgT3X-eWBIx2JA1lj9HhCZzIAGntxU1P9luricxIJrA9ihWq2YYQwgxapGAtVRR9SsfUBRLepKKQHDDiO7GIVNJFCj9Eo8b9--d-V44N4LkNlupqcB02nORzABdpQp&wd=&eqid=f37ac21300035d33000000055839470b [4] Das S K, Kumari A, Bandopadhay D, Akbar S A, Mondal G K. A mathematical model to characterize effects of liquid hold-up on bosh silicon transport in the dripping zone of a blast furnace. Applied Mathematical Modeling, 2011, 35(9): 4208-4221 doi: 10.1016/j.apm.2011.02.045 [5] Zarandi M H F, Ahmadpour P. Fuzzy agent-based expert system for steel making process. Expert Systems with Applications, 2009, 36(5): 9539-9547 doi: 10.1016/j.eswa.2008.10.084 [6] Chao Y C, Su C W, Huang H P. The adaptive autoregressive models for the system dynamics and prediction of blast furnace. Chemical Engineering Communications, 1986, 44(1-6): 309-330 doi: 10.1080/00986448608911363 [7] Hou Z S, Wang Z. From model-based control to data-driven control: survey, classification and perspective. Information Sciences, 2013, 235: 3-35 doi: 10.1016/j.ins.2012.07.014 [8] Hou Z S, Jin S T. Data-driven model-free adaptive control for a class of MIMO nonlinear discrete-time systems. IEEE Transactions on Neural Networks, 2011, 22(12): 2173-2188 doi: 10.1109/TNN.2011.2176141 [9] Zhou P, Lu S W, Chai T Y. Data-driven soft-sensor modeling for product quality estimation using case-based reasoning and fuzzy-similarity rough sets. IEEE Transactions on Automation Science and Engineering, 2014, 11(4): 992-1003 doi: 10.1109/TASE.2013.2288279 [10] Shi L, Li Z L, Yu T, Li J P. Model of hot metal silicon content in blast furnace based on principal component analysis application and partial least square. Journal of Iron and Steel Research, International, 2011, 18(10): 13-16 doi: 10.1016/S1006-706X(12)60015-6 [11] Zhou P, Yuan M, Wang H, Wang Z, Chai T Y. Multivariable dynamic modeling for molten iron quality using online sequential random vector functional-link networks with self-feedback connections. Information Sciences, 2015, 325: 237-255 doi: 10.1016/j.ins.2015.07.002 [12] Yuan M, Zhou P, Li M L, Li R F, Wang H, Chai T Y. Intelligent multivariable modeling of blast furnace molten iron quality based on dynamic AGA-ANN and PCA. Journal of Iron and Steel Research, International, 2015, 22(6): 487-495 doi: 10.1016/S1006-706X(15)30031-5 [13] Tang X L, Zhuang L, Jiang C J. Prediction of silicon content in hot metal using support vector regression based on chaos particle swarm optimization. Expert Systems with Applications, 2009, 36(9): 11853-11857 doi: 10.1016/j.eswa.2009.04.015 [14] Liu Y, Gao Z L. Enhanced just-in-time modelling for online quality prediction in BF ironmaking. Ironmaking and Steelmaking, 2015, 42(5): 321-330 doi: 10.1179/1743281214Y.0000000229 [15] Zeng J S, Gao C H, Su H Y. Data-driven predictive control for blast furnace ironmaking process. Computers and Chemical Engineering, 2010, 34(11): 1854-1862 doi: 10.1016/j.compchemeng.2010.01.005 [16] Marutiram K, Radhakrishnan V R. Predictive control of blast furnaces. In: Proceedings of the 1991 IEEE International Conference on EC3—Energy, Computer, Communication and Control Systems (TENCON'91). New Delhi, India: IEEE, 1991. 488-491 http://www.baidu.com/link?url=MuDOjlNo3q8r0L00dchMZGcD-dDxQzAZl-LL2earkm4VSjaLa1BM4-vmFINazyiF4XvgrzoiRmcjHzZaqDOmYkz9K9nMW-uLR9zJEukynKSxyZPs-RiLGUrBQI0_V2b8nIoYR-RkczB_-ofkcI_q6rNnfCPLIdeVmYBqQGoNutbcL_WRompS03Qyec8LapsPdx745cQAbT_oIm3cR5LWd5_bIh0rZtvUvTft9mhHuAb8PdlXKJWnskPjbdX9vzlXgVABB8wL0yny21dJUZRzXHeOSlNFbyHK2qznD3ofDNu&wd=&eqid=fbf1936200034a930000000558394733 [17] Goethals I, Pelckmans K, Suykens J A K, De Moor B. Subspace identification of Hammerstein systems using least squares support vector machines. IEEE Transactions on Automatic Control, 2005, 50(10): 1509-1519 doi: 10.1109/TAC.2005.856647 [18] Saxén H, Pettersson F. Nonlinear prediction of the hot metal silicon content in the blast furnace. ISIJ International, 2007, 47(12): 1732-1737 doi: 10.2355/isijinternational.47.1732 [19] Phadke M, Wu S M. Identification of multiinput-multioutput transfer function and noise model of a blast furnace from closed-loop data. IEEE Transactions on Automatic Control, 1974, 19(6): 944-951 doi: 10.1109/TAC.1974.1100741 [20] Van Overschee P, De Moor B. N4SID: subspace algorithms for the identification of combined deterministic-stochastic systems. Automatic, 1994, 30(1): 75-93 doi: 10.1016/0005-1098(94)90230-5 [21] Verhaegen M, Dewilde P. Subspace model identification part 1. The output-error state-space model identification class of algorithms. International Journal of Control, 1992, 56(5): 1187-1210 doi: 10.1080/00207179208934363 [22] Larimore W E. Canonical variate analysis in identification, filtering, and adaptive control. In: Proceedings of the 29th Conference on Decision Control. Honolulu, HI: IEEE, 1990. 596-601 http://cn.bing.com/academic/profile?id=2109869845&encoded=0&v=paper_preview&mkt=zh-cn [23] Liu Y, Gao Y C, Gao Z L, Wang H Q, Li P. Simple nonlinear predictive control strategy for chemical processes using sparse kernel learning with polynomial form. Industrial & Engineering Chemistry Research, 2010, 49(17): 8209-8218 http://cn.bing.com/academic/profile?id=2018601772&encoded=0&v=paper_preview&mkt=zh-cn [24] Moon J, Kim B. Enhanced Hammerstein behavioral model for broadband wireless transmitters. IEEE Transactions on Microwave Theory and Techniques, 2011, 59(4): 924-933 doi: 10.1109/TMTT.2011.2110659 [25] 何德峰, 俞立. 约束Hammerstein系统非线性预测控制及其在聚丙烯牌号切换中的仿真研究. 自动化学报, 2009, 35(12): 1558-1563 http://www.aas.net.cn/CN/abstract/abstract13617.shtmlHe De-Feng, Yu Li. Nonlinear predictive control of constrained Hammerstein systems and its research on simulation of polypropylene grade transition. Acta Automatica Sinica, 2009, 35(12): 1558-1563 http://www.aas.net.cn/CN/abstract/abstract13617.shtml [26] Huo H B, Zhu X J, Hu W Q, Tu H Y, Li J, Yang J. Nonlinear model predictive control of SOFC based on a Hammerstein model. Journal of Power Sources, 2008, 185(1): 338-344 doi: 10.1016/j.jpowsour.2008.06.064 [27] Su S W, Wang L, Celler B G, Savkin A V, Guo Y. Identification and control for heart rate regulation during treadmill exercise. IEEE Transactions on Biomedical Engineering, 2007, 54(7): 1238-1246 doi: 10.1109/TBME.2007.890738 [28] Xu S, An X, Qiao X D, Zhu L J, Li L. Multi-output least-squares support vector regression machines. Pattern Recognition Letters, 2013, 34(9): 1078-1084 doi: 10.1016/j.patrec.2013.01.015 -
图(10) / 表(3)
计量
- 文章访问数: 4269
- HTML全文浏览量: 300
- PDF下载量: 892
- 被引次数: 0
