-
摘要: 针对负载未知情况下Buck型DC-DC变换器系统, 基于有限时间控制技术和自适应控制技术, 提出了一种新的快速降压控制算法.首先, 基于时间尺度变换, 对系统的平均状态空间方程进行变换; 然后, 利用饱和有限时间控制理论设计出一类新的快速降压控制算法, 以实现输出电压在有限时间内收敛到参考电压.由于控制器设计过程中考虑了饱和约束条件, 使得变换器的占空比函数满足0到1之间的约束条件.对于负载未知情况, 设计了有限时间观测器以估计未知负载, 最终得到自适应式的有限时间控制算法.与PI控制结果进行了仿真对比, 验证了所提出的控制算法既具有快速的调节性能, 又具有较强的抗负载变化性能.Abstract: For Buck DC-DC converter systems with unknown load variations, a new voltage regulation control algorithm is proposed by using the techniques of finite-time control and adaptive control. First, a time-scale transformation is used for the average state space model of the Buck converter system. Then, based on the saturation finite-time control theory, a new fast voltage regulation control algorithm is designed which can guarantee that the output voltage converges to the reference voltage in a finite time. Because the saturation constraint is considered during the controller design, the duty ratio function of the converter satisfies the constraint between 0 and 1. For an unknown load, a finite-time convergent observer is designed to estimate the unknown load. Finally, an adaptive finite-time control algorithm is developed. Compared with the PI control algorithm, numerical simulations show that the proposed algorithm has a faster regulation performance and stronger performance on load-variation rejection.
-
Key words:
- Buck converter /
- finite-time control /
- adaptive control /
- finite-time observer
-
DC-DC变换器是指能完成直流电路电压转换的电力电子装置, 目前主要应用于直流电压转换、开关电源、直流电机驱动等场合.从功能上来区分, DC-DC变换器可以分为Buck变换器 (降压)、Boost变换器 (升压)、Boost-Buck变换器 (升--降压) 和Buck-Boost变换器 (降--升压) [1].随着现代工业技术的发展, 对直流变换器的要求越来越高, 既要求系统轻便、稳定、可靠, 又要求系统有较高的动态性能.由于DC-DC变换器是一类典型的开关非线性系统, 传统的线性控制设计方法很难保证系统较高的性能.因此, 结合DC-DC变换器模型特点, 研究先进的非线性控制方法已成为电力电子变换器系统研究的一个重要内容.本文主要针对Buck变换器, 提出一种新的非线性控制方法, 以实现电压的快速调节.
目前, 已有不少文献展开对Buck变换器的非线性控制方法研究.文献[2 $-$ 5]分别利用反步法、自适应控制、滑模控制、模糊控制对DC-DC变换器系统设计非线性控制算法, 以提高闭环系统的性能.文献[6]提出通过构造Lyapunov函数来分析和设计一类电力电子变换器的非线性控制系统.文献[7]利用非线性函数设计非线性PI控制器, 比传统线性PI有更好的调节效果和控制性能.文献[8]利用非线性采样输出反馈理论, 设计了一类针对Buck变换器的非线性控制算法, 以提高系统的鲁棒性.文献[9]利用扩展状态观测器, 设计了一类针对Buck变换器的非线性滑模控制算法, 提高了系统抗负载突变的能力.
值得指出的是, 前述所提及的非线性控制算法基本上都要求闭环系统满足局部利普希兹条件, 从而只能保证闭环系统的渐近稳定性[10].从收敛性角度来说, 在实际应用中, 更希望电压能在有限时间内收敛到参考电压.近年来, 有限时间控制算法作为一种新发展的非线性控制算法, 它可以保证闭环系统状态在有限时间内收敛到平衡点.目前, 这种控制方法在理论界[11-16]和应用界[17-23]已得到了广泛的关注.此外, 对于Buck变换器而言, 由于其外部负载常随时间而变化, 如何提高闭环系统抗负载变化能力也是控制算法设计关注的焦点问题之一.当系统存在干扰时, 有限时间控制算法还具有较强的抗负载变化能力, 具体见文献[24]中的理论分析以及文献[17]中的实验验证.文献[25]基于终端滑模控制技术, 对Buck变换器系统设计了有限时间控制器, 但该文献并没有考虑输入饱和受限和负载未知情况.
本文主要针对Buck变换器系统模型特点, 基于有限时间控制理论, 设计了一类有界的非线性自适应控制算法, 以实现电压的快速调节, 并同时满足系统对占空比函数有界约束的要求.首先, 基于时间尺度变换, 引入一个可调的参数, 得到变换后的系统; 然后, 通过构造合适的Lyapunov函数, 设计一类饱和的有限时间控制器; 最后, 利用齐次性理论, 得出系统是有限时间稳定的结论, 即输出电压在有限时间内收敛到参考电压.对负载未知情况, 基于有限时间观测器理论, 设计了自适应控制方法, 以实现对未知负载的估计.本文最后给出仿真实验结果, 并与PI控制算法进行了性能对比.仿真结果表明, 所提出的控制算法使得系统既具有较快的响应速度又有较强的抗负载变化能力.
1. 模型介绍及预备知识
1.1 Buck型DC-DC变换器系统模型
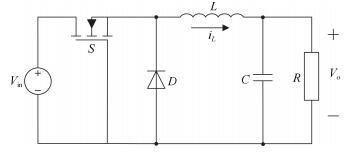
Buck型DC-DC变换器工作原理如图 1所示, 其中 $V_{\rm in}$ 是输入电压, $V_o$ 是输出电压, $S$ 是MOS型开关, $D$ 是二极管, $L$ 、 $C$ 、 $R$ 分别是电感、电容和负载电阻, $i_L$ 是电感电流.在开关频率足够快的情况下, DC-DC变换器可以近似为一般的状态空间模型, 其状态方程为[4]:
$ \begin{align}\label{zhtfc} &\dot i_L=\frac{1}{L} (\mu V_{\rm in}-V_o)\notag\\ &\dot V_o=\frac{1}{C} \left(i_L-\frac{V_o}{R}\right) \end{align} $
(1) 其中, $\mu$ 是控制输入, 即为MOS型开关管 $S$ 的占空比, $\mu \in [0, 1]$ .
假设 $V_{\rm ref}$ 为期望参考输出电压.令 $x_1=V_{\rm ref}-V_o$ 为输出电压误差, 则可以得到误差动态方程为
$ \begin{align}\label{wcdtfc} &\dot x_1=x_2=-\frac{{\rm d}V_o}{{\rm d}t}\notag\\ &\dot x_2=-\frac{1}{LC}x_1-\frac{1}{RC}x_2-\frac{V_{\rm in}}{LC}\mu +\frac{V_{\rm ref}}{LC}\notag\\ &y=x_1 \end{align} $
(2) 1.2 时间尺度坐标变换
为便于控制器设计, 对方程 (2) 进行时间尺度的坐标变换.令 $t=Ms$ , 其中 $M$ 为待设计的一个正常数.定义坐标变换:
$ \begin{align}\label{zbbh} &z_1(s)=x_1(Ms)=x_1(t)\notag \\ &z_2(s)=Mx_2(Ms)=Mx_2(t)\notag \\ &u(s)=M^2\mu(Ms)=M^2\mu(t) \end{align} $
(3) 那么根据式 (2) 可得:
$ \begin{align}\label{bianxing} &\frac{{\rm d}z_1(s)}{{\rm d}s}=\frac{{\rm d}x_1(Ms)}{{\rm d}s}=Mx_2(Ms)=z_2(s)\notag \\ &\quad\frac{{\rm d}z_2(s)}{{\rm d}s}=M\frac{{\rm d}x_2(Ms)}{{\rm d}s}=\notag\\ &\quad -\frac{1}{LC}M^2z_1(s)-\frac{1}{RC}Mz_2(s)-\notag\\ &\quad \frac{V_{\rm in}}{LC}u(s)+\frac{V_{\rm ref}}{LC}M^2 \end{align} $
(4) 为了便于设计控制器, 令
$ \begin{align}\label{canshutihuan} &b_1=\frac{1}{LC}M^2\notag \\ &b_2=\frac{1}{RC}M\notag \\ &f(s)=-\frac{V_{\rm in}}{LC}u(s)+\frac{V_{\rm ref}}{LC}M^2 \end{align} $
(5) 则方程 (2) 可简化为
$ \begin{align}\label{huajianmoxing} &\frac{{\rm d}z_1(s)}{{\rm d}s}=z_2(s)\notag \\ &\frac{{\rm d}z_2(s)}{{\rm d}s}=-b_1z_1(s)-b_2z_2(s)+f(s) \end{align} $
(6) 其中, $b_1>0, b_2>0$ , $f(s)$ 是控制器.
1.3 相关定义和引理
定义1.为了书写方便, 记
$ \begin{align}\label{sig} sig^\alpha(x)={\rm sgn}(x) |x|^\alpha \end{align} $
(7) 其中, $\alpha\geq0$ , $x\in \boldsymbol{R}$ , ${\rm sgn}(\cdot)$ 为符号函数.
定义2.定义一类新的饱和函数
$ \begin{align} sat_{\alpha}(x)=\left\{ {\begin{array}{*{20}c} { {\rm sgn}(x), |x|>1} \\ sig^\alpha(x), |x|\leq1 \end{array}} \right. \end{align} $
(8) 其中, $0\leq\alpha\leq1$ , $x\in \boldsymbol{R}$ .
定义3[4].令 $f(x)=(f_1(x), \cdots, f_n(x))^{\rm T}:{{\mathbf{R}}^{n}}\rightarrow {\bf R}^n$ 为一向量函数.若对任意的 $\varepsilon>0$ , 存在 $(r_1, \cdots, r_n)$ , 其中 $r_i>0, i=1, \cdots, n, $ 使得 $f(x)$ 满足:
$ f_i(\varepsilon^{r_1}x_1, \cdots, \varepsilon^{r_n}x_n)=\varepsilon^{k+r_i}f_i(x), \quad i=1, \cdots, n $
其中, $k>-{\rm min}\{r_i, i=1, \cdots, n\}$ , 则称 $f(s)$ 关于 $(r_1, \cdots, r_n)$ 具有齐次度 $k$ , 其中 $(r_1, \cdots, r_n)$ 称为扩张.
定义4[24].考虑系统
$ \begin{align} \dot x=f(x), x \in U \subseteq {{\mathbf{R}}^{n}}, f(0)=0 \end{align} $
(9) 其中, $f:U\rightarrow \boldsymbol{R}^n$ 为开区域 $U$ 上对 $x$ 连续的函数, 且开区域 $U$ 包含原点.系统的解 $x=0$ 为有限时间稳定当且仅当系统是稳定的且为有限时间收敛的.所谓有限时间收敛指的是:对 $\forall x_0\in U_0\subset {\bf R}^n$ , 存在一个连续函数 $T(x):U_0\setminus\{0\}\rightarrow(0, +\infty)$ , 使得系统 (9) 的解 $x(t, x_0)$ 满足:当 $t\in [0, T(x_0))$ 时, 有 $x(t, x_0)\in U_0\setminus{\{0\}}$ 和 $\lim\nolimits_{x\to T(x_0)}x(t, x_0)=0$ ; 当 $t>T(x_0)$ 时, 有 $x(t, x_0)=0$ .若 $U=U_0={\bf R}^n$ , 则系统是全局有限时间稳定的.
引理1[26].对于如下系统
$ \begin{align} \dot x=f(x)+\hat f(x), \quad x\in {{\mathbf{R}}^{n}} \end{align} $
(10) 其中, $f(x)$ 是连续的齐次向量空间, 且针对扩张 $(r_1, \cdots, r_n)$ 具有齐次度 $k < 0$ , 函数 $\hat f(x)$ 满足 $\hat f(0)=0$ .如果 $x=0$ 是系统 $\dot x=f(x)$ 的渐近稳定平衡点, 且对 $\forall x\neq0$ ,
$ \begin{align} \frac{\hat f_i(\varepsilon^{r_1}x_1, \cdots, \varepsilon^{r_n}x_{n})}{\varepsilon^{r_i+k}}=0, \quad i=1, 2, \cdots, n \end{align} $
(11) 那么 $x=0$ 是系统 (10) 的一个局部有限时间平衡点.如果系统 (10) 既是全局渐近稳定的, 又是局部有限时间稳定的, 那么它是全局有限时间稳定的.
2. 饱和有限时间控制器设计
在本节中, 主要针对坐标变换后的系统 (6) 进行饱和有限时间控制器设计.简便起见, 本节中省略的变量求导都是针对变量 $s$ .
定理1.对于系统 (6), 如果控制器设计成
$ \begin{align} f=-k_1sat_{\alpha_1}(z_1)-k_2sat_{\alpha_2}(z_2) \end{align} $
(12) 其中, $k_1 > 0, k_2 > 0, 0 < \alpha_1 < 1, \alpha_2=2\alpha_1/(1+\alpha_1)$ , 那么系统 (6) 的状态可以在有限时间被镇定到原点, 即在有限时间内, $(z_1(s), z_2(s))=0$ .
证明.证明可分为两个步骤.
步骤1. {证明全局渐近稳定性}
取Lyapunov函数:
$ \begin{align} V=k_1\int_0^{z_1}sat_{\alpha_1}(\rho){\rm d}\rho+\frac{1}{2}b_1z_1^2+\frac{1}{2}z_2^2 \end{align} $
(13) 由于 $\frac{{\rm d}\int_0^{z_1}sat_{\alpha_1}(\rho){\rm d}\rho}{{\rm d}s}=sat_{\alpha_1}(z_1)\dot z_1$ , 那么
$ \begin{align} &\dot V|_{(6)}=k_1sat_{\alpha_1}(z_1)z_2+b_1z_1z_2-b_1z_1z_2-b_2z_2^2+z_2f=\notag\\ &\quad k_1sat_{\alpha_1}(z_1)z_2-b_2z_2^2+z_2f \end{align} $
(14) 在所设计的控制器 (12) 作用下, 可得:
$ \begin{align} &\dot V|_{(6)-(12)}=k_1sat_{\alpha_1}(z_1)z_2-b_2z_2^2-\notag\\ &\quad k_1z_2sat_{\alpha_1}(z_1)-k_2z_2sat_{\alpha_2}(z_2)=\notag\\ &\quad -b_2z_2^2-k_2z_2sat_{\alpha_2}(z_2) \end{align} $
(15) 当 $|z_2|>1$ 时, $z_2sat_{\alpha_2}(z_2)=|z_2|$ , 当 $|z_2|\leq1$ 时, $z_2sat_{\alpha_2}(z_2)=|z_2|^{\alpha_2+1}$ , 故 $\dot V\leq0$ .
记集合 $\Psi=\{(z_1, z_2)|\dot V\equiv0\}$ .由式 (15) 可知 $\dot V\equiv0$ 意味着 $z_2\equiv0$ .亦即 $\dot z_2\equiv0$ .进一步根据式 (6) 和式 (12), 可以得到 $-b_1z_1-k_1sat_{\alpha_1}(z_1)\equiv0$ .注意到 $b_1, k_1$ 为正的增益, 从而 $z_1\equiv0$ .因此, 根据LaSalle不变集原理[27], 可以得出, 当 $s\to0$ 时, $(z_1(s), z_2(s))\to0$ , 即系统 (6) 在控制器 (12) 作用下是渐近稳定的.
步骤2.证明局部有限时间稳定
将闭环系统 (6) 和 (12) 重新写成如下形式:
$ \begin{align} &\dot z_1=z_2\notag\\ &\dot z_2=-k_1sat_{\alpha_1}(z_1)-k_2sat_{\alpha_2}(z_2)+g(z_1, z_2) \end{align} $
(16) 其中, $g(z_1, z_2)=-b_1z_1-b_2z_2$ .
由步骤1证明可知, 系统 (16) 是全局渐近稳定的, 那么系统的状态 $(z_1, z_2)$ 在有限时间内进入区域 $|z_1|\leq1, |z_2|\leq1$ .由饱和函数定义2, 此时系统 (16) 退化成为如下形式:
$ \begin{align} &\dot z_1=z_2\notag\\ &\dot z_2=-k_1sig^{\alpha_1}(z_1)-k_2sig^{\alpha_2}(z_2)+g(z_1, z_2) \end{align} $
(17) 对于系统 (17) 的标称系统:
$ \begin{align} \dot z_1&=z_2\notag\\ \dot z_2&=-k_1sig^{\alpha_1}(z_1)-k_2sig^{\alpha_2}(z_2) \end{align} $
(18) 构造Lyapunov函数如下:
$ \begin{align} W=k_1\int_0^{z_1}sig^{\alpha_1}(\rho) {\rm d}\rho+\frac {1}{2}z_2^2 \end{align} $
(19) 沿着系统 (18), 对式 (19) 进行求导, 得:
$ \begin{align} \dot W|_{(18)}=-k_2z_2sig^{\alpha_2}(z_2)=-k_2|z_2|^{\alpha_2+1} \end{align} $
(20) 故 $\dot W\leq0$ .
通过和步骤1类似的证明, 可以证明对于系统 (18), 当 $s\to\infty$ 时, 有 $(z_1(s), z_2(s))\to0$ , 亦即系统 (18) 是渐近稳定的.
另外由于 $0 < \alpha_1 < 1, \alpha_2=2\alpha_1/(1+\alpha_1)$ , 根据齐次性定义 (即定义3), 可知系统 (18) 的齐次度为 $m=(\alpha_1-1)/2 < 0$ , 其中 $r_1=1, r_2=(\alpha_1+1)/2$ .
接下来证明对于 $\forall(z_1, z_2)\neq(0, 0)$ , 有:
$ \lim\limits_{\varepsilon\to0}\frac{g(\varepsilon^{r_1}z_1, \varepsilon^{r_2}z_2)}{\varepsilon^{r_2+m}}=0 $
根据函数 $g(\cdot)$ 的定义, 有:
$ \begin{align} &\lim\limits_{\varepsilon\to0}\frac{g(\varepsilon^{r_1}z_1, \varepsilon^{r_2}z_2)}{\varepsilon^{r_2+m}}= \lim\limits_{\varepsilon\to0}\frac{-b_1\varepsilon^{r_1}z_1-b_2\varepsilon^{r_2}z_2}{\varepsilon^{r_2+m}}=\notag\\ &\quad \lim\limits_{\varepsilon\to0}(-b_1\varepsilon^{r_1-r_2-m}z_1-b_2\varepsilon^{-m}z_2)\notag \end{align} $
因为 $r_1 > r_2, m < 0$ , 所以 $\lim\nolimits_{\varepsilon\to0}(-b_1\varepsilon^{r_1-r_2-m}z_1-b_2\varepsilon^{-m}z_2)=0$ , 即 $\lim\nolimits_{\varepsilon\to0}\frac{g(\varepsilon^{r_1}z_1, \varepsilon^{r_2}z_2)}{\varepsilon^{r_2+m}}=0$ .因此, 根据引理1可知, 系统 (17) 是全局有限时间稳定的, 亦即系统 (16) 是局部有限时间稳定的.综合步骤1和步骤2, 可以得出系统 (6) 在控制器 (12) 的作用下是全局有限时间稳定.
注1.很显然, 所设计的控制器 (12) 是有界的.根据饱和函数的定义2, 可知 $|f|\leq k_1+k_2$ .因此, 为了满足实际系统对控制器饱和约束的条件, 可以调节控制参数 $k_1, k_2$ 满足任何约束条件.
3. Buck变换器快速有限时间降压控制算法设计
定理2.对于Buck型变换器系统 (1), 如果占空比函数设计成
$ \begin{align} \mu(t)=\frac{V_{\rm ref}}{V_{\rm in}}+\frac{LC}{M^2V_{\rm in}}[k_1sat_{\alpha_1}(x_1(t))+k_2sat_{\alpha_2}(M\cdot x_2(t))] \end{align} $
(21) 其中, $k_1 > 0, k_2 > 0, 0 < \alpha_1 < 1, \alpha_2=2\alpha_1/(1+\alpha_1)$ , 那么系统的输出电压 $V_o$ 可以在有限时间内达到参考电压 $V_{\rm ref}$ .
证明.首先, 对于所设计的控制器 (21), 在时间尺度 $t=Ms$ 变换下有:
$ \begin{align} &\mu(Ms)=\frac{V_{\rm ref}}{V_{\rm in}}+\frac{LC}{M^2V_{\rm in}}[k_1sat_{\alpha_1}(x_1(Ms))+\notag\\ &\quad k_2sat_{\alpha_2}(M\cdot x_2(Ms))] \end{align} $
(22) 在式 (22) 两边同时乘以 $M^2$ , 有:
$ \begin{align} &M^2\cdot\mu(Ms)=\frac{V_{\rm ref}}{V_{\rm in}}M^2+\frac{LC}{V_{\rm in}}[k_1sat_{\alpha_1}(x_1(Ms))+\notag\\ &\quad k_2sat_{\alpha_2}(M\cdot x_2(Ms))] \end{align} $
(23) 基于坐标变换 (3), 可得:
$ \begin{align} u(s)=\frac{V_{\rm ref}}{V_{\rm in}}M^2+\frac{LC}{V_{\rm in}}[k_1sat_{\alpha_1}(z_1(s))+k_2sat_{\alpha_2}(z_2(s))] \end{align} $
(24) 进一步, 根据式 (5) 可得:
$ \begin{align} &f(s)=-\frac{V_{\rm in}}{LC}u(s)+\frac{V_{\rm ref}}{LC}M^2=\notag\\ &\quad -k_1sat_{\alpha_1}(z_1(s))-k_2sat_{\alpha_2}(z_2(s)) \end{align} $
(25) 因此, 基于定理1, 可证明系统 (1) 在控制器 (21) 作用下是全局有限时间稳定的, 即输出电压 $V_o$ 能在有限时间内稳定到参考电压 $V_{\rm ref}$ .
注2.对于所设计的占空比函数 (21), 其大小满足:
$ \begin{align} \frac{V_{\rm ref}}{V_{\rm in}}-\frac{LC}{M^2V_{\rm in}}(k_1+k_2)\leq\mu\leq\frac{V_{\rm ref}}{V_{\rm in}}+\frac{LC}{M^2V_{\rm in}}(k_1+k_2) \end{align} $
(26) 由于 $0 < V_{\rm ref}/V_{\rm in} < 1$ , 因此很方便调节参数 $M, k_1, k_2$ 保证 $0 < \mu < 1$ .
4. Buck变换器快速自适应有限时间降压控制算法设计
本节中, 将考虑负载电阻突变情况下的有限时间降压控制算法设计问题.根据式 (1) 和 (2) 可知, 为了获得状态 $x_2$ , 需要精确知道负载 $R$ .然而实际中负载往往是随时间而变化的.接下来将主要基于有限时间观测器技术对未知负载在有限时间内估计其精确值.
令 $\hat R$ 为未知负载 $R$ 的估计值.为了便于设计, 令 $\theta=-1/R$ 为未知的参数, 令 $\hat\theta$ 为其估计值.
定理3.对于Buck变换器的未知负载电阻, 如果估计器设计为
$ \begin{align} &\dot{\hat{V}}_o=\frac{1}{C}(i_L+\hat\theta V_o)+l_1V_osig^{\beta_1}(V_o-\hat{V}_o)\notag\\ &\dot{\hat{\theta}}=l_2V_osig^{\beta_2}(V_o-\hat{V}_o) \end{align} $
(27) 那么估计值 $\hat\theta$ (或 $\hat R=-1/\hat\theta$ ) 在有限时间内收敛到真实值 $\theta$ (或 $R$ ), 其中 $l_1, l_2$ 为合适的正增益, $0.5 < \beta_1 < 1, \beta_2=2\beta_1-1$ .
证明.定义估计器误差
$ \begin{align} e_1=V_o-\hat{V}_o, e_2=\theta-\hat\theta \end{align} $
(28) 注意到 $\theta$ 是一个常数, 那么根据式 (27) 和 (28) 可得:
$ \begin{align} &\dot{\hat{e}}_1=\frac{V_o}{C}e_2-l_1V_osig^{\beta_1}(e_1)\notag\\ &\dot{\hat{e}}_2=-l_2V_osig^{\beta_2}(e_1) \end{align} $
(29) 基于文献[28]中的定理3.1, 可知存在合适的增益使得该系统是有限时间收敛的, 即估计值 $\hat\theta$ 在有限时间内收敛到真实值 $\theta$ , 亦即负载估计值 $\hat R=-1/\hat \theta$ 在有限时间内收敛到真实负载 $R$ .
基于定理3, 针对Buck变换器负载未知情况, 根据式 (1)、(2) 和式 (21), 可以设计自适应有限时间控制算法的形式如下:
$ \begin{align} &\mu (t)=\frac{V_{\rm ref}}{V_{\rm in}}+\frac{LC}{M^2V_{\rm in}} [k_1sat_{\alpha_1}(x_1(t))+k_2sat_{\alpha_2}(M\hat x_2)]=\notag\\ &\quad \frac{V_{\rm ref}}{V_{\rm in}}+\frac{LC}{M^2V_{\rm in}}[k_1sat_{\alpha_1}(V_{\rm ref}-V_o)+\notag\\ &\quad k_2sat_{\alpha_2}\left[\frac {M}{C}\left(\frac{V_o}{\hat R}-i_L\right)\right] \end{align} $
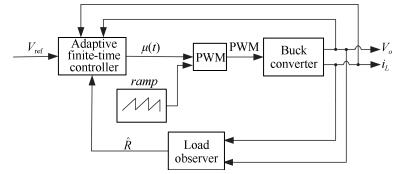
(30) 图 2给出了自适应有限时间电压调节控制算法框图.
图 2 自适应有限时间电压调节控制算法实现框图Fig. 2 The block diagram of adaptive finite-time voltage control algorithm5. 仿真实验
本实验采用针对电力电子及电机拖动开发的专用仿真软件PSIM (Power simulation) 软件进行仿真, 控制策略图见图 2, 其中三角波的频率选择100 kHz.
5.1 系统仿真参数
在仿真中Buck变换器的参数选取为:输入电压 $V_{\rm in}=12$ V, 电感值 $L=5$ mH, 电容值 $C=1 000 \mu$ F, 负载电阻值 $R=30 \Omega$ , 输出参考电压 $V_{\rm ref}=8$ V.为了进行对比, 采用自适应有限时间控制 (Automatic frequency control, AFC) 与PI (Proportional integral control) 控制两种算法.
对于自适应有限时间控制算法式 (30) 和 (27), 参数值分别选为: $M=0.001$ , $k_1=0.225$ , $k_2=1, \alpha_1=1/5$ , $l_1=160$ , $l_2=6, \beta_1=0.55$ .
对于PI控制算法, 其比例和积分增益分别为 $K_P=0.1$ , $K_I=0.05$ .
分别考虑在启动过程、参考电压变化以及负载突变情况下系统动态响应性能.
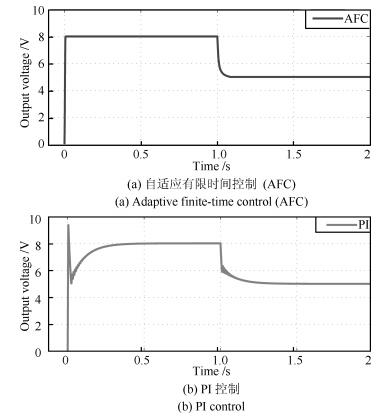
5.2 参考电压变化情况下动态响应
负载保持30 $\Omega$ 不变, 参考电压在1 s时从8 V变化到5 V, 其他参数保持不变.系统动态响应波形见图 3.可以明显看出, 所提出的快速有限时间电压控制算法对参考电压变化的响应速度明显优于PI控制, 其中AFC控制的系统在开始启动时的调节时间是0.007 s, 1 s时参考电压变化时的调节时间是0.06 s; PI控制系统在开始启动时的调节时间是0.32 s, 1 s时参考电压变化时的调节时间是0.24 s.
图 3 两种控制算法作用下输出电压响应曲线 (1 s时, 参考电压由8 V $\to$ 5 V)Fig. 3 The response curves for output voltage under two control algorithms (At 1 second, reference voltage is from 8 V $\to$ 5 V.)5.3 负载突变情况下动态响应
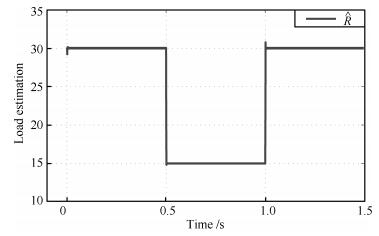
负载电阻变化如下:
$ \begin{align} {R}=\left\{ {\begin{array}{*{20}c} { {30}, 0\leq t\leq0.5 {\rm s}} \\ { {15}, 0.5 {\rm s} < t\leq1 {\rm s}} \\ { {30}, t > 1 {\rm s}} \\ \end{array}} \right. \end{align} $
(31) 其他参数保持不变.可以得到系统响应如图 4.负载电阻估计值响应曲线如图 5.
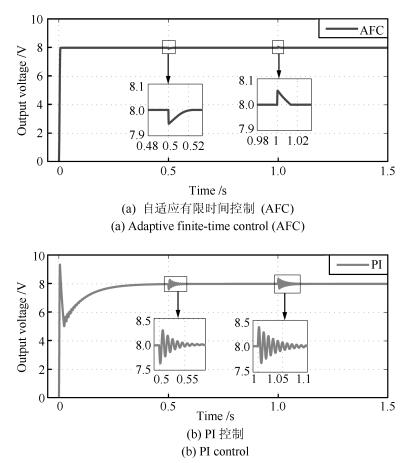图 4 两种控制算法作用下输出电压响应曲线 (0.5 s时, 负载电阻由30 $\Omega\to15 \Omega$ ; 1 s时, 负载电阻由15 $\Omega\to30 \Omega$ )Fig. 4 The response curves for output voltage under two control algorithms (At 0.5 second, load resistance is from 30 $\Omega\to15 \Omega$ ; at 1 second, load resistance is from 15 $\Omega\to30 \Omega$ .AFC控制的系统在负载由30 $\Omega\to 15 \Omega$ 的调节时间为0.018 s, 电压波动范围为7.964 V $\sim$ 8 V, 在负载由15 $\Omega\to 30 \Omega$ 的调节时间为0.013 s, 电压波动范围为8 V $\sim$ 8.054 V。
PI控制的系统在负载由30 $\Omega\to 15 \Omega$ 的调节时间为0.034 s, 电压波动范围为7.631 V $\sim$ 8.365 V, 在负载由15 $\Omega\to 30 \Omega$ 的调节时间为0.048 s, 电压波动范围为7.628 V $\sim$ 8.368 V.
可见, 所提出的快速自适应有限时间降压控制方法对负载突变的响应更快, 电压波动更小.
上述结果表明, 相对于PI控制, 所提出的快速自适应有限时间降压控制算法具有较快的收敛性和较强的抗负载变化能力.
6. 结论
本文利用饱和有限时间控制和自适应控制理论设计出一类新的快速自适应降压控制算法, 使得即使负载未知情况下输出电压仍可以在有限时间内快速达到参考电压.通过构造Lyapunov函数从理论上严格证明了系统的全局有限时间稳定性.最后通过仿真对比, 验证了所提方法的有效性.
-
图 2 自适应有限时间电压调节控制算法实现框图
Fig. 2 The block diagram of adaptive finite-time voltage control algorithm
图 3 两种控制算法作用下输出电压响应曲线 (1 s时, 参考电压由8 V $\to$ 5 V)
Fig. 3 The response curves for output voltage under two control algorithms (At 1 second, reference voltage is from 8 V $\to$ 5 V.)
图 4 两种控制算法作用下输出电压响应曲线 (0.5 s时, 负载电阻由30 $\Omega\to15 \Omega$ ; 1 s时, 负载电阻由15 $\Omega\to30 \Omega$ )
Fig. 4 The response curves for output voltage under two control algorithms (At 0.5 second, load resistance is from 30 $\Omega\to15 \Omega$ ; at 1 second, load resistance is from 15 $\Omega\to30 \Omega$ .
-
[1] 张兴, 杜少武, 黄海宏.电力电子技术.北京:科学出版社, 2010.Zhang Xing, Du Shao-Wu, Huang Hai-Hong. Power Electronics Technology. Beijing:Science Press, 2010. [2] Alvarez-Ramirez J, Espinosa-Pérez G, Noriega-Pineda D. Current-mode control of DC-DC power converters:a backstepping approach. International Journal of Robust and Nonlinear Control, 2003, 13(5):421-442 doi: 10.1002/rnc.v13:5 [3] Tan S C, Lai Y M, Tse C K, Cheung M K H. Adaptive feedforward and feedback control schemes for sliding mode controlled power converters. IEEE Transactions on Power Electronics, 2004, 21(1):182-192 [4] Tan S C, Lai Y M, Tse C K. Techniques and implementation. Sliding Mode Control of Switching Power Converters. Boca Raton:CRC press, 2011. [5] Elmas C, Deperlioglu O, Sayan H H. Adaptive fuzzy logic controller for DC-DC converters. Expert Systems with Applications, 2009, 36(2):1540-1548 doi: 10.1016/j.eswa.2007.11.029 [6] Hu T S. A nonlinear-system approach to analysis and design of power-electronic converters with saturation and bilinear terms. IEEE Transactions on Power Electronics, 2011, 26(2):399-410 doi: 10.1109/TPEL.2010.2054115 [7] 李虹, 尚佳宁, 陈姚, 尚倩, 郝瑞祥.基于fal函数的非线性PI控制器在DC-DC变换器中的应用.电工技术学报, 2014, 29(S1):326-331 http://www.cnki.com.cn/Article/CJFDTOTAL-DGJS2014S1045.htmLi Hong, Shang Jia-Ning, Chen Yao, Shang Qian, Hao Rui-Xiang. The applications of nonlinear PI controller based on the fal function in the DC-DC converter. Transactions of China Electrotechnical Society, 2014, 29(S1):326-331 http://www.cnki.com.cn/Article/CJFDTOTAL-DGJS2014S1045.htm [8] Zhang C L, Wang J X, Li S H, Wu B, Qian C J. Robust control for PWM-based DC-DC buck power converters with uncertainty via sampled-data output feedback. IEEE Transactions on Power Electronics, 2015, 30(1):504-515 doi: 10.1109/TPEL.2014.2299759 [9] Wang J X, Li S H, Yang J X, Wu B, Li Q. Extended state observer-based sliding mode control for PWM-based DC-DC buck power converter systems with mismatched disturbances. IET Control Theory and Applications, 2015, 9(4):579-586 doi: 10.1049/iet-cta.2014.0220 [10] Bhat S P, Bernstein D S. Continuous finite-time stabilization of the translational and rotational double integrators. IEEE Transactions on Automatic Control, 1998, 43(5):678-682 doi: 10.1109/9.668834 [11] 丁世宏, 李世华.有限时间控制问题综述.控制与决策, 2011, 26(2):161-169Ding Shi-Hong, Li Shi-Hua. A survey for finite-time control problems. Control and Decision, 2011, 26(2):161-169 [12] 李世华, 丁世宏, 田玉平.一类二阶非线性系统的有限时间状态反馈镇定方法.自动化学报, 2007, 33(1):101-104 doi: 10.1360/aas-007-0101Li Shi-Hua, Ding Shi-Hong, Tian Yu-Ping. A finite-time state feedback stabilization method for a class of second order nonlinear systems. Acta Automatica Sinica, 2007, 33(1):101-104 doi: 10.1360/aas-007-0101 [13] Shen Y J, Xia X H. Semi-global finite-time observers for nonlinear systems. Automatica, 2008, 44(12):3152-3156 doi: 10.1016/j.automatica.2008.05.015 [14] Shen Y J, Huang Y H. Uniformly observable and globally Lipschitzian nonlinear systems admit global finite-time observers. IEEE Transactions on Automatic Control, 2009, 54(11):2621-2625 doi: 10.1109/TAC.2009.2029298 [15] 丁世宏, 李世华.输入饱和下的非线性积分系统的全局有限时间镇定.自动化学报, 2011, 37(10):1222-1231 http://www.aas.net.cn/CN/abstract/abstract17611.shtmlDing Shi-Hong, Li Shi-Hua. Global finite-time stabilization of nonlinear integrator systems subject to input saturation. Acta Automatica Sinica, 2011, 37(10):1222-1231 http://www.aas.net.cn/CN/abstract/abstract17611.shtml [16] Zhai J Y. Global finite-time output feedback stabilisation for a class of uncertain non-triangular nonlinear systems. International Journal of Systems Science, 2014, 45(3):637-646 doi: 10.1080/00207721.2012.724113 [17] Li S H, Zhou M M, Yu X H. Design and implementation of terminal sliding mode control method for PMSM speed regulation system. IEEE Transactions on Industrial Informatics, 2013, 9(4):1879-1891 doi: 10.1109/TII.2012.2226896 [18] 李向阳.基于有限时间跟踪微分器的迭代学习控制.自动化学报, 2014, 40(7):1366-1374 http://www.aas.net.cn/CN/abstract/abstract18408.shtmlLi Xiang-Yang. Iterative learning control based on finite time tracking differentiator. Acta Automatica Sinica, 2014, 40(7):1366-1374 http://www.aas.net.cn/CN/abstract/abstract18408.shtml [19] Zhu Y K, Guan X P, Luo X Y. Finite-time consensus of heterogeneous multi-agent systems with linear and nonlinear dynamics. Acta Automatica Sinica, 2014, 40(11):2618-2624 doi: 10.1016/S1874-1029(14)60408-0 [20] 李雪冰, 马莉, 丁世宏.一类新的二阶滑模控制方法及其在倒立摆控制中的应用.自动化学报, 2015, 41(1):193-202 http://www.aas.net.cn/CN/abstract/abstract18598.shtmlLi Xue-Bing, Ma Li, Ding Shi-Hong. A new second-order sliding mode control and its application to inverted pendulum. Acta Automatica Sinicae, 2015, 41(1):193-202 http://www.aas.net.cn/CN/abstract/abstract18598.shtml [21] 王芳, 陈鑫, 何勇, 吴敏.联合连通条件下的二阶多智能体系统有限时间一致性控制.控制理论与应用, 2014, 31(7):981-986 http://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201407020.htmWang Fang, Chen Xin, He Yong, Wu Min. Finite-time consensus control of second-order multi-agent systems with jointly-connected topologies. Control Theory and Applications, 2014, 31(7):981-986 http://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201407020.htm [22] Liu S C, Geng Z Y, Sun J Y. Finite-time attitude control:a finite-time passivity approach. IEEE/CAA Journal of Automatica Sinica, 2015, 2(1):102-108 doi: 10.1109/JAS.2015.7032911 [23] 董琦, 宗群, 王芳, 田栢苓.基于光滑二阶滑模的可重复使用运载器有限时间再入姿态控制.控制理论与应用, 2015, 32(4):448-455 http://youxian.cnki.com.cn/yxdetail.aspx?filename=KZLY20150512000&dbname=CAPJ2015Dong Qi, Zong Qun, Wang Fang, Tian Bai-Ling. Finite time smooth second-order sliding-mode controller design for reentry reusable launch vehicle. Control Theory and Applications, 2015, 32(4):448-455 http://youxian.cnki.com.cn/yxdetail.aspx?filename=KZLY20150512000&dbname=CAPJ2015 [24] Bhat S P, Bernstein D S. Finite-time stability of continuous autonomous systems. SIAM Journal on Control and Optimization, 2000, 38(3):751-766 doi: 10.1137/S0363012997321358 [25] Komurcugil H. Non-singular terminal sliding-mode control of DC-DC buck converters. Control Engineering Practice, 2013, 21(3):321-332 doi: 10.1016/j.conengprac.2012.11.006 [26] Hong Y G, Xu Y S, Huang J. Finite-time control for robot manipulators. Systems and Control Letters, 2002, 46(4):243-253 doi: 10.1016/S0167-6911(02)00130-5 [27] Khalil H K. Nonlinear Systems (3rd Edition). Englewood, NJ, USA:Prentice Hall, 2002. 303-334 [28] Du H B, Qian C J, Yang S Z, Li S H. Recursive design of finite-time convergent observers for a class of time-varying nonlinear systems. Automatica, 2013, 49(2):601-609 doi: 10.1016/j.automatica.2012.11.036 期刊类型引用(20)
1. 陈强，王满意，南余荣. Buck型变换器预设时间自适应反演控制. 高技术通讯. 2024(03): 302-311 . 
百度学术2. 王会明，彭炜炜，谭鑫，陈晓雷. 基于滑模控制的DC-DC降压变换器实验平台. 电气电子教学学报. 2024(01): 218-222 . 百度学术3. 从永正，程盈盈，胡正. 基于三阶超螺旋滑模观测器算法的机器人力矩估计方法. 控制理论与应用. 2023(07): 1208-1215 . 百度学术4. 王会明，谭鑫，彭炜炜，陈晓雷. DC-DC降压转换器控制系统虚拟实验平台设计. 实验室科学. 2023(06): 39-44 . 百度学术5. 黄曦，刘宜成，涂海燕，周凯. Buck变换器的新型非奇异固定时间滑模控制. 电气传动. 2022(04): 31-35 . 百度学术6. 陈维乐，都海波. 一种基于齐次系统理论的二阶离散超螺旋控制算法. 控制理论与应用. 2022(04): 761-769 . 百度学术7. 吴悔，黄世沛，曾国强，张正江. 基于事件触发的Buck型DC-DC变换器有限时间控制. 计算机测量与控制. 2022(05): 81-86 . 百度学术8. 陈强，杨晨冰，南余荣. 基于变速趋近律的Buck型变换器抗扰动控制. 控制与决策. 2021(04): 893-900 . 百度学术9. 南余荣，陈姝瑾，王满意. 基于GPI观测器的Buck型变换器趋近律控制. 计算机测量与控制. 2021(08): 89-94 . 百度学术10. 韩冰，李继岚，黄尚安，雷友建. 基于PID控制的Buck型开关电源研究. 工业控制计算机. 2021(09): 157-158 . 百度学术11. 孙训红，陈维乐，都海波，李世华. 基于输出反馈和滑模控制的一类二阶非线性系统有限时间镇定方法. 控制理论与应用. 2021(11): 1727-1734 . 百度学术12. 刘继，张小平，张瑞瑞. 基于FTC的BBMC调速控制策略及参数优化. 自动化学报. 2020(02): 332-341 . 本站查看13. 陈强，钱宁，南余荣. Buck型变换器固定时间自适应控制. 控制与决策. 2020(05): 1183-1190 . 百度学术14. 王艳敏，PAULO Fecundo Adelson，于玲，牛子铭，英钊. 未建模动态对Buck变换器滑模控制系统的影响分析. 自动化学报. 2020(11): 2472-2478 . 本站查看15. 张春燕，盛安冬，戚国庆，李银伢. 基于反步法的有限时间机器人环航控制器设计. 自动化学报. 2019(03): 540-552 . 本站查看16. 钱宁，陈强，杨宇，南余荣. Buck型变换器非奇异固定时间滑模控制. 计算机测量与控制. 2019(06): 62-65+74 . 百度学术17. 郑则炯，梁文祯. 适用于低功耗DC-DC变换器的双延迟线结构DPWM. 电子器件. 2018(04): 877-881 . 百度学术18. 王宇野，王羽翔. Buck变换器的非奇异终端滑模控制. 闽南师范大学学报(自然科学版). 2018(03): 44-48 . 百度学术19. 张春燕，戚国庆，李银伢，盛安冬. 一种基于有限时间稳定的环绕控制器设计. 自动化学报. 2018(11): 2056-2067 . 本站查看20. 李健，沈艳军，刘允刚. Buck型变换器输出跟踪的自适应动态规划算法. 控制理论与应用. 2017(03): 393-400 . 百度学术其他类型引用(22)
-
下载:
下载:
计量
- 文章访问数: 2385
- HTML全文浏览量: 249
- PDF下载量: 1094
- 被引次数: 42
