非线性先进控制软件SMART-NLS及其应用
-
摘要: 本文介绍了由清华大学自动化系开发的非线性先进控制软件的原理和功能,并给 出了其一个仿真应用.仿真说明该先进控制器完全实现了非线性先进控制技术,对非线性 系统有很好控制效果,可以预计在现代流程工业中必将有着广泛的应用前景和可观的效益.
-
反馈控制[1]是工业过程自动控制的基本原理, 起源于18世纪的瓦特原理[2], 一种比例作用的反馈控制, 如果在比例项的基础上加入积分项和微分项[3], 这就是比例积分微分(Proportional-integral-derivative, PID)控制器[4-8].在20世纪40年代形成了以奈奎斯特(Nyquist)提出的奈氏稳定判据[9]、伊文斯(Evans)提出的根轨迹法[9]等为核心的经典控制论[9-10], 推动了PID控制技术在工业过程控制的广泛应用.
随后在20世纪50年代末现代控制论[10]出现, 主要有原苏联科学家庞特里亚金(Pontryagin)提出的极大值原理、美国学者贝尔曼(Bellman)创立的动态规划和卡尔曼(Kalman)建立的卡尔曼滤波理论[11-12]等.经过半个多世纪的发展, 产生出宏大和严密的现代控制论和众多的先进控制策略[13-21], 例如模型预测控制(Model predictive control, MPC)[17-20]等.从20世纪70年代开始, 系统辨识技术[22-25]以及计算机技术的高速发展[26], 强有力地推动了现代控制论在工业过程中的应用.
文献[19]论述了MPC对电力工业复杂系统的重要性和意义, MPC的主要特点是能够容易地处理控制约束问题.在火电厂的过程控制系统, 约束优化有可能使过程控制量尽量紧贴系统安全允许的下限值, 能够显著地提高火电厂运行的经济性; 客观上, 由于存在过程的不确定性问题, 约束优化的优势也伴随着风险的共存, 例如容易造成过程控制量的超限, 不利于火电厂运行的安全; 文献[20]指出: “目前预测控制理论和算法的主要成果是针对线性系统的, 由于实际应用领域中存在大量非线性控制问题, 这方面的研究特别是应用还很不成熟”.
在控制科学的发展过程中, 还产生出种类丰富的、介于经典控制与先进控制之间的一类高性能控制策略:例如基于神经网络的PID[27]、基于改进粒子群算法的PID[28]、基于改进遗传算法的PID[29]、Smith预估控制器[30-31]、内模控制器(Internal model controller, IMC)[32-33]、内模PID[34]、自适应鲁棒控制器[35-36]、$ {H}_{\infty} $鲁棒控制器[37]、滑模控制器[38]等.
现代控制论的理论成果虽然完善和严密, 但是客观上并没有撼动PID控制在工业过程控制的基础地位. 1989年，韩京清[39]发表在《系统科学与数学》上的论文“控制理论:模型论还是控制论”, 反映了他对现代控制论的观点.韩京清认为控制理论有两个迴然不同的思考方式:模型论和控制论, 前者“靠系统的数学模型去找控制律的方法”, 后者依靠的则是系统的“某些响应特征或过程的某些实时信息”.
高志强[2]指出了长期并存于控制科学的3个范式: “工业范式、模型范式和抗扰范式”.模型范式代表了现代控制论的思维方式和世界观[2], “建模-优化”是先进控制的共性所在.高志强[2]同时还指出: “工程控制中的被控对象大都是非线性、时变而且未知的”.这一观点表明:在控制实际中还存在大量的不确定性问题, 准确的数学模型难以获取, “建模-优化”对于不确定性基本没有意义.目前来看, 抑制不确定性问题的最有效方法仍然是包括PID在内的反馈控制或者反馈校正[40-41].这说明在提高反馈控制性能的方面还有很大的发展空间.
值得关注的是:韩京清[42]提出了不依赖模型的自抗扰控制技术(Active disturbance rejection control, ADRC), 指出了控制的核心是抗扰, 为人们重新认识控制问题的本质和指导解决实际的控制问题提供了一种全新的思路. ADRC是一种以扩张状态观测器(Extended state observation, ESO)[43]为核心的新型控制技术, 带宽与误差的反比关系[2, 44]是ADRC的显著特点, 通过调整ESO的频率带宽[45]能够实现任意精度跟踪扰动.通过近20年的发展, ADRC的研究和应用成果已经较为丰富[45-51].
滤波的优劣也是决定控制性能的一个重要性因素, 例如滤波相位包括时间的滞后造成控制回路稳定裕度下降.韩京清[42]从非线性最速跟踪(Nonlinear optimal tracking, NOT)[52]的角度提出了非线性跟踪微分器(Nonlinear tracking differentiator, NTD)[52-54].相对线性跟踪微分器(Linear tracking differentiator, LTD)[55], NTD显著提高了跟踪输入微分的“效率”.但是NOT跟踪输入和NTD跟踪输入微分的特性还与输入的幅值有关.
在火电厂的过程控制实践中, 新型控制策略包括新型滤波方法和新型观测方法等取得了良好的进展; 文献[56-58]从正弦跟踪(Sinusoid tracking, ST)的角度分别提出了一种正弦跟踪滤波器(Sinusoid tracking filter, STF)[56]和一种正弦跟踪微分器(Sinusoid tracking differentiator, STD)[57-58]. STF跟踪输入和STD跟踪输入微分的滞后较小, 并且跟踪特性与输入幅值无关; 文献[59]提出了一种基于并联降阶(Parallel reduction order, PRO)和高增益PI (High gain of PI, HGPI)控制器的内反馈控制(Internal feedback control, IFC)方法, 核心是一种内反馈器(Internal feedback device, IFD). IFD的实质是一种控制过程的并联降阶器, 通过PRO作用, 将HGPI实际控制的阶次降低为一阶, 有效提高了IFC在大滞后过程的控制性能.所谓大滞后是高阶较大惯性和较大纯滞后特性的一种简称.通常认为:在大滞后过程, 纯滞后比例在30 %以上时, 则属于一种难控过程.文献[60]提出了一种新型抗扰控制方法(New disturbance rejection control, NDRC), 主要适用于低阶过程的抗扰控制.
针对在控制实际中存在的纯滞后问题, 本文提出了一种新型超前观测(New advanced observer, NAO)方法, 提供了一种在频率特性上针对纯滞后过程的超前观测, 这是NAO与一些超前观测的显著区别所在; 针对在控制实际中存在的不确定性问题, 本文提出了一种基于NAO、IFC、STF的新型高性能控制器(New higher performance controller, NHPC).
长期以来, 在过程控制领域, 包括在火电厂过程控制实际, 形成了以PID控制为主, 先进控制、高性能控制、自抗扰控制、新型控制等共存的基本现状.
注.本文中变量(包括符号)的表达具有唯一性, 可相互引用; 出于表述简洁性的需要, 文中对使用到的变量单位进行统一.如文中无特别说明, 时间包括时间常数的单位为s, 频率包括频率带宽的单位为rad/s, 增益包括幅频增益的单位无量纲, 相位包括相频相位和相位稳定裕度的单位为$ ^\circ $, 阶次的单位无量纲.
1. 正弦跟踪滤波器
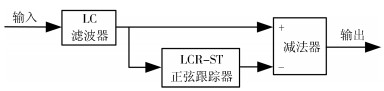
STF[56]是用于构造新型高性能控制器, 即NHPC的重要基础之一. STF来源于一种二阶惯性滤波器(Second order inertial filter, SOIF)的内部结构[56], 一种由LC滤波器(LC filter, LCF)[56]和LCR[26]正弦跟踪器(LCR sinusoid tracking, LCR-ST)[56]构造的结构, 如图 1所示.
图 1 二阶惯性滤波器内部结构示意图Fig. 1 The inside structure diagram of second order inertial filterLCR-ST是一种LCR带通滤波器[26].在图 1中, 如果用文献[56]提出的一种新型正弦跟踪器(New sinusoid tracking, NST)[56]取代LCR-ST, 则得到STF.构造NST的基础是一种正交混频方法[61-62].
SOIF和STF的传递函数分别表达为
$$ \begin{align} & W_{\rm SOIF } (s) = \frac{1}{{(1 + T_{\rm SOIF } s)^2 }} \\ & W_{\rm SOIF } (s) = W_{\rm LC} (s)[1 - W_{{\rm LCR} {\text -} {\rm ST}} (s)] \\ & W_{\rm STF } (s) = W_{\rm LC} (s)[1 - W_{\rm NST} (s)] \\ & W_{\rm LC} (s) = \frac{1}{{1 + (T_{\rm SOIF } s)^2 }} \\ & W_{{\rm LCR} {\text -} {\rm ST}} (s) = \frac{{2T_{\rm SOIF } s}} {{(1 + T_{\rm SOIF } s)^2 }} \end{align} $$ (1) 式中, $ {W}_{ {\rm{SOIF}}}(s) $为SOIF的传递函数, $ {W}_{ {\rm{STF}}}(s) $为STF的传递函数, $ {T}_{ {\rm{SOIF}}} $为惯性时间常数, $ {W}_{ {\rm{LC}}}(s) $为LCF的传递函数, $ {W}_{ {\rm{LCR-ST}}}(s) $为LCR-ST的传递函数, $ {W}_{ {\rm{NST}}}(s) $为NST的传递函数. $ {T}_{ {\rm{SOIF}}} $也代表LCF和STF的滤波时间常数.
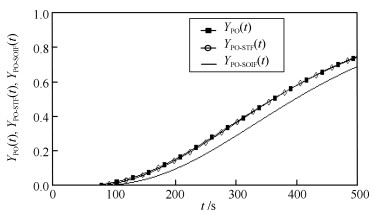
为了说明STF的滤波特性, 对式(6)给出的过程对象(Process object, PO)在单位阶跃激励的过程输出分别进行SOIF和STF滤波.用$ {Y}_{ {\rm{PO}}}(t) $表达PO的过程输出, 用$ {Y}_{ {\rm{PO-STF}}}(t) $和$ {Y}_{ {\rm{PO-SOIF}}}(t) $分别表达STF和SOIF跟踪$ {Y}_{ {\rm{PO}}}(t) $的输出.其中在PO参数为: $ n = 4 $, $ {T}_{\alpha} = 100 $ s, $ {K}_{\alpha} = 1 $, $ {T}_{ {\rm{SOIF}}} = 20 $ s, 得到的实验结果如图 2所示.
由图 2可见, STF跟踪$ {Y}_{ {\rm{PO}}}(t) $的特性远优于SOIF.
由于STF跟踪输入的滞后较小, 通常在工程计算上不考虑STF.
2. 新型超前观测方法
超前观测是利用一些超前策略获取过程响应的超前信息, 对于提高过程控制性能具有重要意义.超前策略有多种形式, 例如ESO[43]、微分器[52-58]、2阶惯性逆模型(Second order inertial inverse model, SOIIM)[56]、比例微分(Proportion differentiation, PD)控制器[63]、相位超前校正[64]等.
在控制实际中, 惯性滞后过程(Inertial lag process, ILP)是普遍存在的.其中惯性逆模型(Inertial inverse model, IIM)可以实现针对ILP的超前观测.在理想情况下, IIM能够观测到ILP的输入; 由于理论与实际之间存在偏差, 2阶以上高阶IIM (Higher order IIM, HOIIM)在工程上的意义不大.
在控制实际中, 纯滞后过程也是普遍存在的, 相对于惯性滞后, 纯滞后的阶次无穷大; Smith预估控制器[30-31]是一种基于对象数学模型和针对过程纯滞后补偿的一种高性能控制策略.在控制实际中准确模型包括准确纯滞后难以获取, Smith预估控制运用并不普遍.
目前的超前观测对于纯滞后过程没有针对性, 为了解决这个问题, 本文提出了一种新型超前观测方法, 即NAO.
理论上, 纯滞后逆(Pure lag inverse，PLI)是一种针对纯滞后过程的理想超前观测器(Ideal advanced observation, IAO), 表达为
$$ \begin{align} & W_{\rm IAO} (s) = {\rm e } ^{T_{\rm AO} s} \\ & W_{\rm IAO} ({\mathop{\rm j}\nolimits} \omega ) = G_{\rm IAO} (\omega ){\rm e } ^{{\rm j } PH_{\rm IAO} (\omega )} \end{align} $$ (2) 式中, $ {W}_{ {\rm{IAO}}}(s) $为IAO的传递函数, $ {T}_{ {\rm{AO}}} $为超前观测时间常数, $ {W}_{ {\rm{IAO}}}( {\rm{j}}\omega) $为IAO的频域函数, $ \omega $为正弦频率. $ {G}_{ {\rm{IAO}}}(\omega) $为IAO的幅频增益, $ {PH}_{ {\rm{IAO}}}(\omega) $为IAO的相频相位.
但是IAO是一种非实时的超前观测, 在实时系统中无法实现.
控制科学也是一种实验科学[2], 通过大量的实验计算, 本文找到了一种在频域特性上近似IAO的方法, 即NAO, 表达为
$$ \begin{align*} & W_{\rm NAO} (s) = \frac{{1.2\sum\limits_{i = 1}^{i = 5} {(1 + 0.8\, T_{\rm AO} s)^i } }}{{\sum\limits_{i = 1}^{i = 6} {(1 + 0.4\, T_{\rm AO} s)^i } }} \\ & W_{\rm NAO} ({\rm j } \omega ) = G_{\rm NAO} (\omega ) {\rm e } ^{{\rm j } PH_{\rm NAO} (\omega )} \end{align*} $$ $$ \begin{align} & \omega _{\rm AO} = \frac{1}{{T_{\rm AO} }}{{\rm{ }}} \end{align} $$ (3) 式中, $ W_{ {\rm{NAO}}}(s) $为NAO的传递函数, $ W_{ {\rm{NAO}}}( {\rm{j}}\omega) $为NAO的频域函数, $ G_{ {\rm{NAO}}}(\omega) $为NAO的幅频增益, $ PH_{ {\rm{NAO}}}(\omega) $为NAO的相频相位, $ \omega_{ {\rm{AO}}} $为超前观测频率带宽.
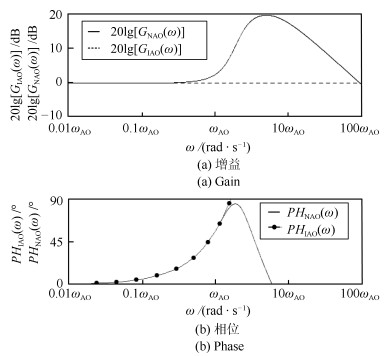
根据式(2)和式(3), 得到IAO和NAO的频率特性的计算结果, 如图 3所示.
在图 3中, $ {G}_{ {\rm{IAO}}}(\omega) $和$ {G}_{ {\rm{NAO}}}(\omega) $采用对数dB增益.在$ \omega_{ {\rm{AO}}} $以内, NAO与IAO相比的相位误差(Phase error)小于0.5 $ ^\circ $. NAO的高频增益趋于0, 具有较好的噪声干扰滤波特性.
$ \omega_{ {\rm{AO}}} $与$ {T}_{ {\rm{AO}}} $的反比关系是NAO的基本特性.在系统频率带宽(System frequency bandwidth, SFB) $ \omega_{ {\rm{SFB}}}<\omega_{ {\rm{AO}}} $时, NAO能够提供在时间超前上相对准确的观测.
直观地了解NAO的特性, 对PO在单位阶跃激励的过程输出进行NAO观测.其中在PO参数为: $ n = 4, $ $ T_{\alpha} = 80\, $s, $ K_{\alpha} = 1 $, 得到$ \omega_{ {\rm{SFB}}}\thickapprox 0.00543 $ rad/s, 设置$ \omega_{ {\rm{AO}}} = 0.01 $ rad/s或$ T_{ {\rm{AO}}} = 100 $ s.得到的实验结果如图 4所示.
在图 4中, $ Y_{ {\rm{PO-NAO}}}(t) $为$ Y_{ {\rm{PO}}}(t) $的NAO输出, 可见NAO对$ Y_{ {\rm{PO}}}(t) $具有较好的超前观测性能.
过程响应的本身已经携带了各种信息, 例如过程模型的信息、耦合作用的信息、不确定性扰动信息等.采用NAO能够提前获取这些信息, 对于提高大滞后过程的控制性能具有积极意义.
NAO是用于构造新型高性能控制器, 即NHPC的重要基础之一.
3. 新型高性能控制器
为了能够较好地解决大滞后过程控制中的不确定性的抑制问题, 本文提出了一种基于NAO、IFC[59]包括STF[56]的新型高性能控制器, 即NHPC, 如图 5所示.
在图 5中, 函数发生器(Function generator, FG)用于简单的过程轨迹控制, IFD由内反馈器A (IFD of A, IFD-A)和内反馈器B (IFD of B, IFD-B)所组成.外扰通过扰动模型(Disturbance model, DM)直接叠加在PO的过程输出中, 相当于施加了一种外部耦合作用.
NHPC与IFC的主要区别是, 如果取消NHPC中的NAO, 则得到IFC.
NHPC是一种将IFC中的IFD拆分为IFD-A和IFD-B的结构, 表达为
$$ \begin{align*} W_{\rm IFD} (s) = W_{{\rm IFD} {\text -} {\rm A}} (s) + W_{{\rm IFD} {\text -} {\rm B}} (s) = \nonumber \end{align*} $$ $$ \begin{align} &\, K_{\rm IFD } \frac{{T_{\rm IFD } s}}{{(1 + T_{\rm IFD } s)^2 }} \!\sum\limits_{i = 0}^{i = n - 2}\! {\left(\frac{1}{{1 + T_{\rm IFD } s}}\right)^i } \\ W_{{\rm IFD} {\text -} {\rm A}} (s) = &\, K_{\rm IFD } \frac{{T_{\rm IFD } s}} {{(1 + T_{\rm IFD } s)^2 }} \\ W_{{\rm IFD} {\text -} {\rm B}} (s) = &\, \frac{K_{\rm IFD }{T_{\rm IFD } s}} {{(1 + T_{\rm IFD } s)^3 }}\sum\limits_{i = 0}^{i = n - 3} {\left(\frac{1}{{1 + T_{\rm IFD } s}}\right)^i } \end{align} $$ (4) 其中, $ {W}_{ {\rm{IFD}}}(s) $为IFD的传递函数, $ {W}_{ {\rm{IFD-A}}}(s) $为IFD-A的传递函数, $ {W}_{ {\rm{IFD-B}}}(s) $为IFD-B的传递函数. $ {K}_{ {\rm{IFD}}} $为IFD的增益, $ {T}_{ {\rm{IFD}}} $为统一的时间常数, n为整数阶次.
在NHPC中, HGPI与IFD-A构成了一种内部PID控制器(Inside PID, IPID), 表达式为
$$ \begin{align} W_{\rm IPID} (s) \approx &\ \frac{1}{{W_{{\rm IFD} {\text -} {\rm A}} (s)}} = \\ &\ \frac{1}{{K_{\rm IFD} }}[2 + \frac{1}{{T_{\rm IFD} s}} + T_{\rm IFD} s] \end{align} $$ (5) 其中, $ {W}_{ {\rm{IPID}}}(s) $为IPID的传递函数.
研究结果表明, 将NAO放在反馈通道或者放在IPID后面, 在外扰抑制上没有区别.如果将NAO放在反馈通道, 主要问题是对输出跟踪输入的速度有较大的影响.因此, 实际将NAO放在IPID的后面.
不考虑STF, 则IFD-B是PO的一种PRO, 表达式为
$$ \begin{align} & \mathop {W_{\rm PO } (s)}\limits_{n \ge 3} = \frac{{K_\alpha }} {{(1 + T_\alpha s)^n }} \\ & W_{\rm PRO } (s) = W_{{\rm IFD} {\text -} {\rm B}} (s) + W_{\rm PO } (s) = \frac{{K_\alpha }}{{(1 + T_\alpha s)^2 }} \\ & K_{\rm IFD } = K_\alpha , \; \; \; {{\rm{ }}}T_{\rm IFD } = T_\alpha {{\rm{ }}} \end{align} $$ (6) 其中, $ {W}_{ {\rm{PO}}}(s) $为PO的传递函数, $ {K}_{\alpha} $为PO的增益, $ {T}_{\alpha} $为PO的惯性时间常数, $ {W}_{ {\rm{PRO}}}(s) $为IFD-B与PO并联的传递函数.
由式(6)可知, 如果PO模型已知, 则IFD-B与PO模型并联的结果得到二阶惯性环节, IPID实际控制的是二阶惯性环节, 这就是PRO的作用.
不考虑STF, 得到NHPC开环频域函数为
$$ \begin{align} & W_{{\rm N } {\rm HPC } \text{-} {\rm OL } } ({\rm j } \omega ) = \\ &\qquad \frac{{W_{\rm IPID } ({\rm j } \omega )W_{\rm NAO} ({\rm j } \omega )W_{{\rm PO } } ({\rm j } \omega )}}{{1 + W_{{\rm IPID } } ({\rm j } \omega )W_{\rm NAO} ({\rm j } \omega )W_{{\rm IFD} \text{-} {\rm B}} ({\rm j } \omega )}} = \\ &\qquad G_{{\rm N } {\rm HPC } \text{-} {\rm OL } } (\omega ){\rm e } ^{{\rm j } PH_{{\rm N } {\rm HPC } \text{-} {\rm OL } } (\omega )} \end{align} $$ $$ \begin{align} & \mathop {PM_{{\rm N } {\rm HPC } \text{-} {\rm OL } } } \limits_{G_{{\rm N } {\rm HPC } \text{-} {\rm OL } } (\omega ) = 1} = 180 + PH_{{\rm N } {\rm HPC } \text{-} {\mathop{\rm OL}\nolimits} } (\omega ) \end{align} $$ (7) 其中, $ {W}_{ {\rm{NHPC-OL}}}( {\rm{j}}\omega) $为NHPC的开环系统频域函数. $ {W}_{ {\rm{IPID}}}( {\rm{j}}\omega) $、$ {W}_{ {\rm{NAO}}}( {\rm{j}}\omega) $、$ {W}_{ {\rm{PO}}}( {\rm{j}}\omega) $、$ {W}_{ {\rm{IFD-B}}}( {\rm{j}}\omega) $分别为IPID、NAO、PO、IFD-B的频域函数. $ {G}_{ {\rm{NHPC-OL}}}(\omega) $为NHPC的开环系统幅频增益. $ {PH}_{ {\rm{NHPC-OL}}}(\omega) $为NHPC的开环系统相频相位. $ {PM}_{ {\rm{NHPC-OL}}} $为NHPC的开环系统相位稳定裕度.
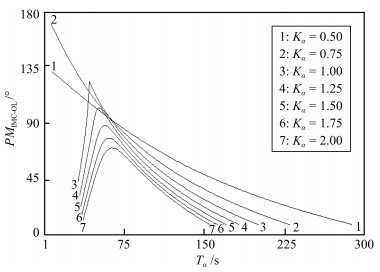
具体在PO参数为: $ n = 4 $, $ {T}_{\alpha} $变化范围为1 $ \sim $ 300 s, $ {K}_{\alpha} $变化范围为0.5 $ \sim $ 2.0. IFD参数为: $ {T}_{ {\rm{IFD}}} $ $ = $ $ 100 $ s, $ {K}_{ {\rm{IFD}}} = 1 $. NAO参数为: $ {T}_{ {\rm{AO}}} = 100 $ s.得到$ {PM}_{ {\rm{NHPC-OL}}} $的计算结果, 如图 6所示.
图 6 NHPC开环系统相位稳定裕度Fig. 6 The diagram of open loop system phase stability margin of NHPC通过对图 6的分析可知, 给出的7条$ {PM}_{ {\rm{NHPC-OL}}} $随$ {T}_{\alpha} $变化的曲线基本在$ {PM}_{ {\rm{NHPC-OL}}} $ $ = $ $ 90\, ^\circ $和$ {T}_{\alpha}\thickapprox 80 $ s处交会, 说明NAO起到了一种在频率特性上的“聚合作用”.可以认为:在$ {T}_{\alpha} $ $ = $ $ 80 $ s时, $ {PM}_{ {\rm{NHPC-OL}}} $基本不随$ {K}_{\alpha} $变化, 这是一个有价值的重要特性, 表明了在7条曲线的交会区, 对过程的非线性具有较好的抑制性能.
出于对比需要, 根据第5节给出的PID参数, 用$ {PM}_{ {\rm{PID-OL}}} $表达PID开环系统相位稳定裕度.在相同的过程变化条件下, 得到$ {PM}_{ {\rm{PID-OL}}} $的计算结果, 如图 7所示.
图 7 PID开环系统相位稳定裕度Fig. 7 The diagram of open loop system phase stability margin of PID由图 7可见, 给出的7条$ {PM}_{ {\rm{PID-OL}}} $随$ {T}_{\alpha} $变化的曲线没有共同的交会区, 而且$ {PM}_{ {\rm{PID-OL}}} $随$ {K}_{\alpha} $变化的发散度较大, 表明了PID抑制过程非线性的性能较差.客观地看问题, 在$ {K}_{\alpha}>1 $时, 稳定范围在$ {T}_{\alpha} $的下限优于NHPC, 这是事物的矛盾性所决定的.
4. 新型高性能控制器与内模控制器的对比
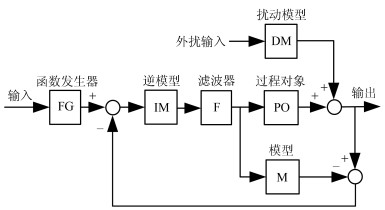
内模控制器(IMC)[32-33]是一种基于过程数学模型进行控制器设计的高性能控制策略.基本的IMC系统如图 8所示.
在图 8中, IMC系统由FG、逆模型(Inverse model, IM)、滤波器(Filter, F)、模型(Model, M)、PO、DM等构成.
不考虑FG, IMC闭环传递函数为
$$ \begin{align} & W_{{\rm IMC} {\text -} {\rm CL}} (s) = \\ & \quad\ \ \frac{{W_{\rm IM} (s)W_{\rm F} (s)W_{\rm PO } (s)}}{{1 - W_{\rm IM} (s)W_{\rm F} (s)[W_{\rm M} (s) - W_{\rm PO } (s)]}} = W_{\rm F} (s) \\ & W_{\rm M} (s) = W_{\rm PO } (s) \\ & W_{\rm IM} (s)W_{\rm M} (s) = 1 \end{align} $$ (8) 其中, $ {W}_{ {\rm{IMC-CL}}}(s) $为IMC的闭环传递函数. $ {W}_{ {\rm{IM}}}(s) $为IM的传递函数. $ {W}_{ {\rm{F}}}(s) $为F的传递函数. $ {W}_{ {\rm{M}}}(s) $为M的传递函数.
由式(8)可知, 在M与PO传递函数匹配、IM与M传递函数相乘等于1的情况下, IMC的闭环传递函数等于F的传递函数.
由于理论与实际之间存在较大的偏差, 在控制实际中准确的模型难以获取, 高于2阶的IM在工程的意义不大.工程上, IM的阶次不宜超过2阶.
出于研究的需要, 定义IM为SOIIM[56], F为SOIF[56], M为高阶惯性模型(High order inertial model, HOIM), 表达式为
$$ \begin{align} & W_{\rm IM}(s) = K_{\rm IM } (1 + T_{\rm IM } s)^2 \\ & W_{\rm F} (s) = \frac{1}{{(1 + T_{\rm F } s)^2 }} \\ & W_{\rm M} (s) = \frac{K_{\rm M} }{{(1 + T_{\rm M} s)^n }} \\ & K_{\rm IM } K_{\rm M} = 1 \end{align} $$ (9) 其中, $ {K}_{ {\rm{IM}}} $为IM的增益, $ {T}_{ {\rm{IM}}} $为IM的惯性时间常数; $ {T}_{ {\rm{F}}} $为F的惯性滤波时间常数; $ {K}_{ {\rm{M}}} $为M增益, $ {T}_{ {\rm{M}}} $为M的惯性时间常数.
IMC开环系统频域函数为
$$ \begin{align} & W_{{\rm IMC} {\text -} {\rm OL}} ({\rm j} \omega ) = \\ &\qquad \frac{{W_{\rm IM} ({\rm j} \omega )W_{\rm F} ({\rm j} \omega )W_{\rm PO } ({\rm j} \omega )}} {{1 - W_{\rm IM} ({\rm j} \omega )W_{\rm F} ({\rm j} \omega )W_{\rm M} ({\rm j} \omega )}} = \\ &\qquad G_{{\rm IMC} {\text -} {\rm OL}} (\omega ){\rm e} ^{{\mathop{\rm j}\limits} PH_{{\rm IMC} {\text -} {\rm OL}} (\omega )} \\ & \mathop {PM_{{\rm IMC} {\text -} {\rm OL}} }\limits_{G_{{\rm IMC} {\text -} {\rm OL}} (\omega ) = 1} = 180 + PH_{{\rm IMC} {\text -} {\rm OL}} (\omega ) \end{align} $$ (10) 其中, $ {W}_{ {\rm{IMC-OL}}}( {\rm{j}}\omega) $为IMC的开环系统频域函数. $ {W}_{ {\rm{IM}}}( {\rm{j}}\omega) $, $ {W}_{ {\rm{F}}}( {\rm{j}}\omega) $, $ {W}_{ {\rm{M}}}( {\rm{j}}\omega) $分别为IM, F, M的频域函数; $ {G}_{ {\rm{IMC-OL}}}(\omega) $为IMC的开环系统幅频增益, $ {PH}_{ {\rm{IMC-OL}}}(\omega) $为IMC的开环系统相频相位, $ {PM}_{ {\rm{IMC-OL}}} $为IMC的开环系统频域相位稳定裕度.
具体在IM参数为: $ {T}_{ {\rm{IM}}} = 80 $ s, $ {K}_{ {\rm{IM}}} = 1 $. F参数为: $ {T}_{ {\rm{F}}} = 10 $ s. M参数为: $ n = 4 $, $ {T}_{ {\rm{M}}} = 80 $ s, $ {K}_{ {\rm{M}}} $ $ = $ $ 1 $.在与图 6相同的过程变化条件下, 得到$ {PM}_{ {\rm{IMC-OL}}} $的计算结果, 如图 9所示.
图 9 IMC开环系统相位稳定裕度Fig. 9 The diagram of open loop system phase stability margin of IMC通过将图 9与图 6进行对比可以发现, 在相同的过程变化条件下, IMC抑制过程不确定性的性能明显不如NHPC, 具体表现在: $ {PM}_{ {\rm{IMC-OL}}} $随$ {T}_{\alpha} $和$ {K}_{\alpha} $变化的稳定范围相对较窄, 表明了IMC的鲁棒性能不如NHPC.在图 9中, 给出的7条$ {PM}_{ {\rm{IMC-OL}}} $随$ {T}_{\alpha} $变化的曲线没有共同的交会区, 表明了IMC抑制过程非线性的性能不如NHPC.
5. 仿真实验
为了考察NHPC的控制性能, 在数字计算机上进行了仿真实验, 其中数值离散计算间隔为1 s.本文主要从抑制不确定性的方面考察NHPC的控制性能.
由于在控制实际中PID运用比较普遍, 因此在仿真实验上, 主要将NHPC控制与PID控制进行对比.
出于仿真实验需要, 简单考虑, FG和DM均采用二阶惯性环节, 表达式为
$$ \begin{align} & W_{\rm FG } (s) = \frac{1}{{(1 + T_{\rm FG1 } s)(1 + T_{\rm FG2 } s)}} \\ & W_{\rm DM } (s) = \frac{1}{{(1 + T_{\rm DM } s)^2 }} \end{align} $$ (11) 其中, $ {W}_{ {\rm{FG}}}(s) $为FG的传递函数, $ {T}_{ {\rm{FG1}}} $和$ {T}_{ {\rm{FG2}}} $为FG的2个惯性时间常数. $ {W}_{ {\rm{DM}}}(s) $为DM的传递函数, $ {T}_{ {\rm{DM}}} $为DM的惯性时间常数.
用$ {PV}_{ {\rm{NHPC}}}(t) $和$ {PV}_{ {\rm{PID}}}(t) $分别表达NHPC和PID控制的过程输出, 用$ {CO}_{ {\rm{NHPC}}}(t) $和$ {CO}_{ {\rm{PID}}}(t) $分别表达NHPC和PID控制器的输出.其中控制输入和外扰采用阶跃信号.
PID中的微分作用采用实际微分环节[65], 一种理想微分(Ideal differentiation, ID)[57-58]和一阶惯性滤波(First order inertial filter, FOIF)的串级结构.对PID参数整定的原则是:在输入阶跃变化时, 过程输出不出现超调, 目的是保证PID对确定性对象具有较好的控制特性, 能够更真实地进行对比.
PID表达式为
$$ \begin{align} W_{\rm PID} (s) = K_{\rm p } + \frac{1}{{T_{\rm i} s}} + K_{\rm d} \frac{{T_{\rm d } s}}{{1 + T_{\rm d } s}} \end{align} $$ (12) 其中, $ W_{ {\rm{PID}}}(s) $为PID的传递函数, $ K_{ {\rm{p}}} $为比率增益, $ T_{ {\rm{i}}} $为积分时间常数, $ K_{ {\rm{d}}} $为实际微分增益, $ T_{ {\rm{d}}} $为实际微分时间常数.
在PO参数为: $ n = 4 $, $ K_{\alpha} = 1 $, $ T_{\alpha} = 80 $ s. IFD参数为: $ K_{ {\rm{IFD}}} = 1 $, $ T_{ {\rm{IFD}}} = 100 $ s. STF参数为: $ T_{ {\rm{SOIF}}} $ $ = 10 $ s. NAO参数为: $ T_{ {\rm{AO}}} = 100 $ s. FG参数为: $ T_{ {\rm{FG1}}} = 100 $ s, $ T_{ {\rm{FG2}}} = 50 $ s. DM参数为: $ T_{ {\rm{DM}}} $ $ = $ $ 80 $ s; 另外, 经多次调整, 得到PID参数为: $ K_{ {\rm{p}}} = $ $ 0.75 $, $ T_{ {\rm{i}}} = 295 $ s, $ T_{ {\rm{d}}} = 100 $ s, $ K_{ {\rm{d}}} = 0.35 $.之后文中如无特别说明, 保持上述参数不变.
其中, 输入为1, 外扰为0.5, 得到的实验结果如图 10所示.
图 10 控制特性仿真实验结果(意图 1)Fig. 10 The results of control characteristic simulation (NO. 1)之后文中如无特别说明, 均默认输入为1和外扰为0.5.
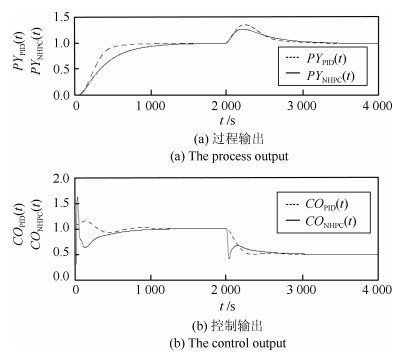
将$ T_{\alpha} = 80 $ s改为$ T_{\alpha} = 50 $ s, 得到的实验结果如图 11所示.
图 11 控制特性仿真实验结果(意图 2)Fig. 11 The results of control characteristic simulation (NO. 2)将$ K_{\alpha} = 1 $改为$ K_{\alpha} = 2. $得到的实验结果如图 12所示.
图 12 控制特性仿真实验结果(意图 3)Fig. 12 The results of control characteristic simulation (NO. 3)图 12给出的实验结果说明: NHPC在抑制过程增益变化的性能上明显优于PID.
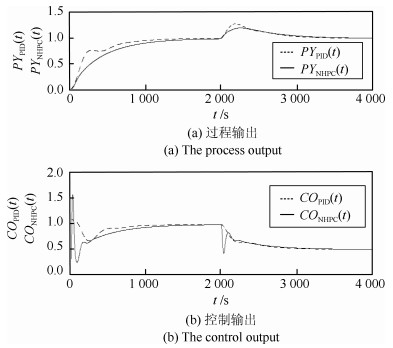
在PO中增加125 s的纯滞后, 得到的实验结果如图 13所示.
图 13 控制特性仿真实验结果(意图 4)Fig. 13 The results of control characteristic simulation (NO. 4)图 13给出的实验结果说明: NHPC在抑制过程时间变化的性能上明显优于PID.
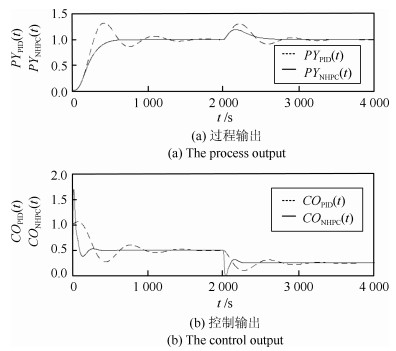
在PO中增加125 s的纯滞后, 并且对过程输出$ PV_{ {\rm{PID}}}(t) $和$ PV_{ {\rm{NHPC}}}(t) $进行指数处理, 具体为$ [PV_{ {\rm{PID}}}(t)]^{1.25} $和$ [PV_{ {\rm{NHPC}}}(t)]^{1.25} $, 目的是模拟较弱非线性的大滞后过程.得到的实验结果如图 14所示.
图 14 控制特性仿真实验结果(意图 5)Fig. 14 The results of control characteristic simulation (NO. 5)图 14给出的实验结果说明: NHPC在抑制大滞后过程的较弱非线性的性能上明显优于PID.
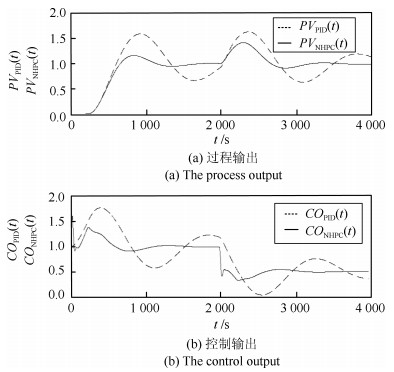
在PO中增加200 s的纯滞后, 得到的实验结果如图 15所示.
图 15 控制特性仿真实验结果(意图 6)Fig. 15 The results of control characteristic simulation (NO. 6)在图 15中, 纯滞后所占比例为38 %, 属于一种难控过程.实验结果说明, 在不改变NHPC参数的前提下, NHPC对于难控过程仍然具有良好的控制性能.如果改变NHPC的参数则对于纯滞后比例60 %以内的大滞后难控过程也具有良好的控制性能.
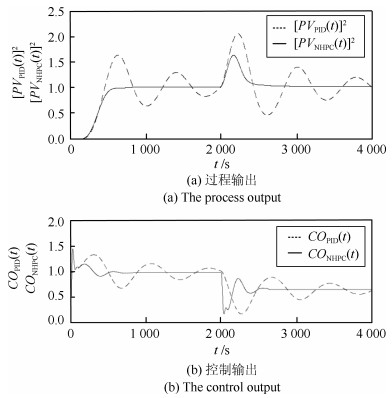
在PO中增加50 s的纯滞后, 并且对过程输出$ PV_{ {\rm{PID}}}(t) $和$ {PV}_{ {\rm{NHPC}}}(t) $进行平方处理, 即$ [PV_{ {\rm{PID}}}(t)]^{2} $和$ [PV_{ {\rm{NHPC}}}(t)]^{2} $, 目的是模拟较强非线性的大滞后过程.得到的实验结果如图 16所示.
图 16 控制特性仿真实验结果(意图 7)Fig. 16 The results of control characteristic simulation (NO. 7)图 16给出的实验结果说明: NHPC在抑制大滞后过程的较强非线性的性能上明显优于PID.
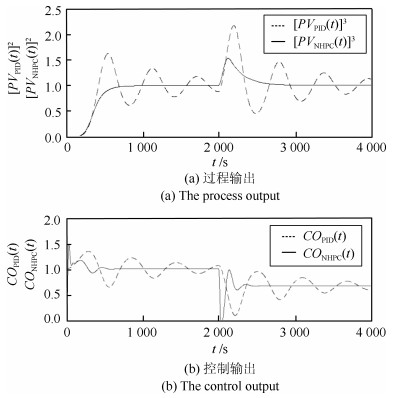
对过程输出$ PV_{ {\rm{PID}}}(t) $和$ PV_{ {\rm{NHPC}}}(t) $进行立方处理, 即$ [PV_{ {\rm{PID}}}(t)]^{3} $和$ [PV_{ {\rm{NHPC}}}(t)]^{3} $, 目的是模拟超强非线性的大滞后过程.得到的实验结果如图 17所示.
图 17 控制特性仿真实验结果(意图 8)Fig. 17 The results of control characteristic simulation (NO. 8)图 17给出的实验结果说明: NHPC在抑制大滞后过程的超强非线性的性能上显著优于PID.
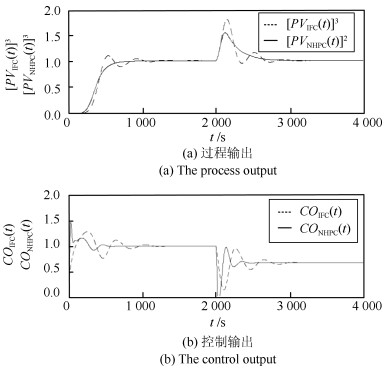
在图 17实验结果的基础上, 取消NHPC中的NAO, 则得到IFC控制.用$ CO_{ {\rm{IFC}}}(t) $和$ PV_{ {\rm{IFC}}}(t) $分别表达IFC的控制器输出和过程输出.得到的实验结果如图 18所示.
图 18 控制特性仿真实验结果(意图 9)Fig. 18 The results of control characteristic simulation (NO. 9)图 18给出的实验结果说明: NHPC在控制性能上优于IFC.
由图 10 $ \sim $ 17实验结果可见, 相对PID控制, NHPC在抑制大滞后过程的不确定性问题上具有显著的优势.
从输入控制输出的角度看, NAO有效减小了控制输出的波动范围, 具有良好的稳定性.
6. 实际应用
将本文NHPC运用于某火电厂的1 000 MW燃煤机组的锅炉主控系统的优化.锅炉主控系统用于控制锅炉主汽压力, 控制手段是通过控制锅炉燃煤量的变化达到控制锅炉主汽压力的目的.
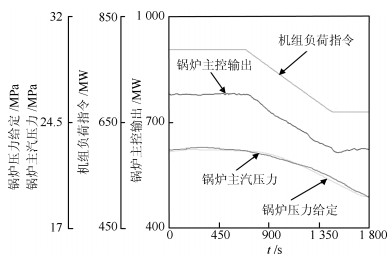
所述锅炉主控系统采用常规PID控制, 主要存在问题是在机组变负荷过程, 锅炉主汽压力的波动较大.其中的一段控制趋势, 如图 19所示.
图 19 优化前锅炉主控系统控制特性示意图Fig. 19 The control properties of boiler master control system before optimization由图 19可见, 锅炉主控输出的波动较大, 主要是前馈控制量不准确引起的.在变负荷过程, 锅炉主汽压力跟踪锅炉压力给定的的最大动态偏差为1.17 MPa.
需要指出:由于PID控制性能不高, 前馈控制相对重要, 前馈控制起到了一种解耦[66-67]作用.
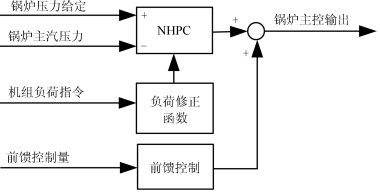
采用NHPC对所述主汽压力控制系统进行优化, 主要目的是改善锅炉主汽压力跟踪锅炉压力给定的动态特性, 如图 20所示.
在图 20中, 负荷修正函数[59]用于在不同的负荷指令下, 修正NHPC的参数, 主要作用是对过程的慢时变问题有较好的跟踪特性.
其中在机组750 MW负荷, 通过现场试验测得锅炉主控输出-主汽压力对象的二阶模型(Second order model, SOM)为
$$ \begin{eqnarray} G_{\rm SOM }(s) = \frac{{0.87}}{{(1 + 246s)(1 + 355s)}} \end{eqnarray} $$ (13) 其中, $ G_{ {\rm{SOM}}}(s) $为SOM的传递函数, 但并不代表实际对象一定是二阶的, 其中还包含有纯滞后的因数等.
为了简化NHPC参数整定, 采用了工程参数整定方法(Engineering parameter tuning method, EPTM).主要根据SOM的滞后时间$ T_{0.63} $, 为过程值上升到过程终值0.63的时间.然后给出一个整数工程阶次$ {n}_{ {\rm{eng}}} $, 最后将$ {T}_{0.63} $平均分配给IFD, 得到IFD的参数.
根据式(13)给出的SOM传递函数, 对应的$ {T}_{0.63} $ $ \approx $ $ 631 $ s, 实际设置$ {n}_{ {\rm{eng}}} = 8 $, 得到IFD参数为
$$ \begin{align} & n_{\rm eng } = 8 \\ & K_{\rm IFD } = 0.87 \\ & T_{\rm IFD } = \frac{{T_{0.63} }}{{n_{\rm eng } }} = \frac{{631}}{8} \approx 79 \end{align} $$ (14) 实际设置NAO参数为: $ T_{ {\rm{AO}}} = 200 $ s.
采用NHPC优化后, 其中在机组800 MW $ \rightarrow $ 600 MW的降负荷过程, 得到主汽压力的控制特性, 如图 21所示.
图 21 优化后锅炉主控系统控制特性示意图Fig. 21 The control properties of boiler master control system after optimization由图 21可见, 在采用NHPC优化后, 锅炉主控输出变化相对平稳.在变负荷过程, 锅炉主汽压力跟踪锅炉压力给定的动态偏差一般不超过0.51 MPa, 如果采用IFC优化, 一般不超过0.68 MPa.可见, 采用NHPC优化收到了明显的效果.
需要指出: NHPC中的NAO具有一定的解耦作用, 前馈控制相对不重要.
7. 结论
本文指出在过程控制领域, 包括在火电厂过程控制实际, 形成了以PID控制为主, 先进控制、高性能控制、自抗扰控制、新型控制等共存的基本现状.对在火电厂过程控制实践中出现的新型控制策略进行了总结.
采用并联降阶方法、即PRO, 是提高包括PID在内低阶控制器在大滞后过程控制性能的有效途径. STF较好解决了滤波滞后的问题, NAO提供了一种在频率特性上针对纯滞后过程的超前观测. PRO、STF、NAO等具有一般性意义; 针对在大滞后过程控制中存在的不确定性问题, 将NAO和IFC包括STF等有机结合, 构造出一种新型高性能控制器、即NHPC, 在较宽的范围内, 对大滞后过程的时变性包括非线性等不确定性问题具有较好的抑制性能; 本文提出的方法是对控制理论的有益发展, 具有重要的理论研究和工程应用价值.数学分析、仿真实验和实际电力控制工程应用的结果, 验证了本文所提出观点和方法的正确性和有效性.
致谢: 广东电网有限责任公司副总工程师肖祥对促进新型控制技术的形成做出了历史性和关键性贡献, 广东电科院能源技术有限责任公司副总经理廖宏楷、南方电网高级技术专家刘石对推动新型控制技术进入到广东省发电系统的商业应用起到了重要作用, 谨致以诚挚的谢意. 期刊类型引用(4)
1. 连传强，郭力源，许观达，肖飞，张伟伟. 永磁伺服系统转速跟踪控制与数据驱动的参数设计方法. 电工技术学报. 2024(08): 2412-2421 . 
百度学术2. 李军，黄卫剑，陈锦攀，石上瑶，陈鹏云，梁爽. 一种位域比例观测器及其在火电机组过程控制中的应用. 广东电力. 2023(02): 135-142 . 百度学术3. 李军，黄卫剑，陈锦攀，李德波，张远. 一种适应新型电力系统的火电机组煤质在线校正方法. 广东电力. 2023(04): 118-123 . 百度学术4. 李军，黄卫剑，陈锦攀，王朋，周永言，朱亚清，潘凤萍，李德波. 一种适应新型电力系统深度调峰快速调频的工程最速控制器. 广东电力. 2021(08): 110-119 . 百度学术其他类型引用(1)
-
下载:
计量
- 文章访问数: 1288
- HTML全文浏览量: 88
- PDF下载量: 824
- 被引次数: 5
下载:
