考虑方向约束与最短偏航路径的双旋翼无人机轨迹规划

韩京良; 于海; 张兆鹏; 何慰; 梁潇; 方勇纯

doi:10.16383/j.aas.c250434

考虑方向约束与最短偏航路径的双旋翼无人机轨迹规划

doi: 10.16383/j.aas.c250434 cstr: 32138.14.j.aas.c250434

韩京良^{1, 2,},
于海^{2, 3,},
张兆鹏^{2, 3,},
何慰^{2, 3,},
梁潇^{2, 3},
方勇纯^{2, 3,}

1.
南开大学卓越工程师学院天津 300350
2.
南开大学智能技术与机器人系统研究院深圳 518083
3.
南开大学机器人与信息自动化研究所天津 300350

基金项目: 国家自然科学基金(U25A20473, 62273187), 天津市重点研发计划科技支撑重点项目(23YFZCSN00060)资助

详细信息

作者简介:
韩京良：南开大学卓越工程师学院硕士研究生. 主要研究方向为无人机结构设计与轨迹规划. E-mail: hanjl@mail.nankai.edu.cn

于海：南开大学机器人与信息自动化研究所博士研究生. 主要研究方向为无人机的非线性控制. E-mail: yuhai@mail.nankai.edu.cn

张兆鹏：南开大学机器人与信息自动化研究所博士研究生. 主要研究方向为飞行机械臂的运动规划与任务规划. E-mail: zhangzp@mail.nankai.edu.cn

何慰：南开大学机器人与信息自动化研究所博士研究生. 主要研究方向为机器人的运动规划, 状态估计和智能控制. E-mail: howei@mail.nankai.edu.cn

梁潇：南开大学机器人与信息自动化研究所副教授. 主要研究方向为无人机系统的运动规划和非线性控制. E-mail: liangx@nankai.edu.cn

方勇纯：南开大学机器人与信息自动化研究所教授. 主要研究方向为非线性控制, 机器人视觉伺服控制, 欠驱动系统控制和基于原子力显微镜的纳米系统. 本文通信作者. E-mail: fangyc@nankai.edu.cn

计量
- 文章访问数: 7
- HTML全文浏览量: 5
- 被引次数: 0
出版历程
- 收稿日期: 2025-08-31
- 录用日期: 2026-01-12
- 网络出版日期: 2026-01-28

Twin Tiltrotor UAV Trajectory Planning Considering Directional Constraints and Shortest-yaw Paths

HAN Jing-Liang^{1, 2
,},
YU Hai^{2, 3
,},
ZHANG Zhao-Peng^{2, 3
,},
HE Wei^{2, 3
,},
LIANG Xiao^{2, 3},
FANG Yong-Chun^{2, 3
,}

1.
College of Elite Engineers, Nankai University, Tianjin, 300350
2.
Institute of Intelligence Technology and Robotic System, Nankai University, Shenzhen, 518083
3.
Institute of Robotics and Automatic Information System, Nankai University, Tianjin, 300350

Funds: Supported by National Natural Science Foundation of China (U25A20473, 62273187) and Key Technologies R&D Program of Tianjin (23YFZCSN00060)

More Information

Author Bio:
HAN Jing-Liang　Master student at the College of Elite Engineers, Nankai University. His research interests include UAV structural design and trajectory planning

YU Hai　Ph. D. candidate at the Institute of Robotics and Automatic Information System, Nankai University. His main research interest is nonlinear control of unmanned aerial vehicles

ZHANG Zhao-Peng　Ph. D. candidate at the Institute of Robotics and Automatic Information System, Nankai University. His research interest covers motion planning and task planning of aerial manipulator systems

HE Wei　Ph. D. candidate at the Institute of Robotics and Automatic Information System, Nankai University. His research interests include motion planning, state estimation, and intelligent control of robots

LIANG Xiao　Associate professor at the Institute of Robotics and Automatic Information System, Nankai University. His research interests include motion planning and nonlinear control of unmanned aerial vehicle systems

FANG Yong-Chun　Professor at the Institute of Robotics and Automatic Information System, Nankai University. His research interests include nonlinear control, robot visual servoing control, control of underactuated systems and AFM-based nanosystems. Corresponding author of this paper

摘要

摘要: 传统多旋翼无人机广泛应用于工业检测、物资运输和灾后搜救等任务. 然而在狭窄空间内, 其飞行往往受到机体尺寸和姿态调节能力的限制, 影响通行效率与飞行安全性. 为此, 面向串联倾转双旋翼无人机平台, 提出一种针对受限环境下考虑方向约束并基于平面速度分量计算偏航角的轨迹生成策略. 该方法改进了最小二阶加速度(SNAP)轨迹生成方法, 实现对位置与偏航轨迹的协调优化, 并设计最短偏航路径算法和航点附近插值平滑算法来提升飞行过程的平滑性与安全性. 将所提方法与不考虑偏航方向约束的最小SNAP方法进行对比, 结果表明改进后的最小SNAP方法更加适用于双旋翼无人机平台. 进一步通过丰富的实验验证了所提方法的有效性与适用性.
- 串联倾转双旋翼无人机 /
- 轨迹规划 /
- 方向约束 /
- 最短边飞行 /
- 最短偏航路径
Abstract: The traditional multi-rotor unmanned aerial vehicle (UAV) is widely used in tasks such as industrial inspection, cargo transportation, disaster search and rescue. However, in confined spaces, their flight is often limited by vehicle size and attitude adjustment capabilities, thereby affecting passability efficiency and flight safety. To address this, a trajectory generation strategy considering directional constraints and calculating yaw angle from horizontal velocity components is proposed for the tandem twin tiltrotor UAV platform in constrained environments. This proposed method improves the minimum second-order acceleration (SNAP) trajectory generation approach, enabling coordinated optimization of position and yaw trajectories, a shortest-yaw path algorithm and an interpolation smoothing algorithm near waypoints are designed to enhance the smoothness and safety of the flight process. Comparative results with the minimum SNAP method, which does not consider yaw direction constraints, demonstrate that the improved method is more suitable for twin tiltrotor UAV platforms. Furthermore, the effectiveness and applicability of the proposed method are validated through extensive experiments.
- Tandem twin tiltrotor UAV /
- trajectory planning /
- directional constraints /
- shortest-edge flight /
- shortest-yaw paths

HTML全文

图 1 串联倾转双旋翼无人机平台

Fig. 1 Tandem twin tiltrotor UAV platform

下载: 全尺寸图片幻灯片

图 2 修正前后的偏航角比较

Fig. 2 Comparison of yaw angles before and after correction

下载: 全尺寸图片幻灯片

图 3 插值平滑前后的偏航角比较

Fig. 3 Comparison of yaw angles before and after interpolation smoothing

下载: 全尺寸图片幻灯片

图 4 Gazebo仿真环境下的双旋翼无人机模型

Fig. 4 Twin Tiltrotor UAV model in the Gazebo simulation environment

下载: 全尺寸图片幻灯片

图 5 Gazebo环境下的模拟场景

Fig. 5 Simulation scene in the Gazebo environment

下载: 全尺寸图片幻灯片

图 6 轨迹一: 弧形轨迹

Fig. 6 Trajectory 1: Arc trajectory

下载: 全尺寸图片幻灯片

图 7 轨迹二: 弯曲折线轨迹

Fig. 7 Trajectory 2: Curved polyline trajectory

下载: 全尺寸图片幻灯片

图 8 轨迹三: 沙漏形轨迹

Fig. 8 Trajectory 3: Hourglass shaped trajectory

下载: 全尺寸图片幻灯片

图 9 场景一: 正方形轨迹(宽阔区域)

Fig. 9 Scene 1: Square trajectory flight (wide area)

下载: 全尺寸图片幻灯片

图 10 场景二: 正方形轨迹(狭窄区域)

Fig. 10 Scene 2: Square trajectory flight (narrow area)

下载: 全尺寸图片幻灯片

表 1 相关研究对比

Table 1 Comparison of related studies

相关研究	研究平台	研究领域	是否考虑方向约束	验证方式
Wang等^[9]	四旋翼无人机	轨迹规划	否	仿真+ 实验
林惠韩等^[11]	共轴双旋翼无人机	制导控制	否	仿真
Qin等^[16]	串联双旋翼无人机	结构设计	否	实验
姬博洋等^[23]	滑翔飞行器	制导控制	是	仿真
雷刚等^[24]	导弹武器系统	轨迹规划	是	仿真
He等^[25]	串联双旋翼无人机	控制规划	否	仿真+ 实验
本文方法	串联双旋翼无人机	轨迹规划	是	仿真+ 实验

下载: 导出CSV

表 2 轨迹一航点坐标及参考偏航角

Table 2 Waypoint coordinates and reference yaw angles of trajectory 1

航点	时间$ t $ (s)	$ x $ (m)	$ y $ (m)	$ z $ (m)	$ \psi_{\rm{ref}} $ (rad)
$ P_0 $	0	$ \phantom{-}0.7 $	$ -0.7 $	$ 1.0 $	$ -1.25\pi $
$ P_1 $	6	$ -0.7 $	$ -0.7 $	$ 1.0 $	$ -1.75\pi $
$ P_2 $	12	$ -0.7 $	$ \phantom{-}0.7 $	$ 1.0 $	$ -2.25\pi $
$ P_3 $	18	$ \phantom{-}0.7 $	$ \phantom{-}0.7 $	$ 1.0 $	$ -2.75\pi $
$ P_4 $	24	$ \phantom{-}0.7 $	$ -0.7 $	$ 1.0 $	$ -3.25\pi $

下载: 导出CSV

表 3 轨迹二航点坐标及参考偏航角

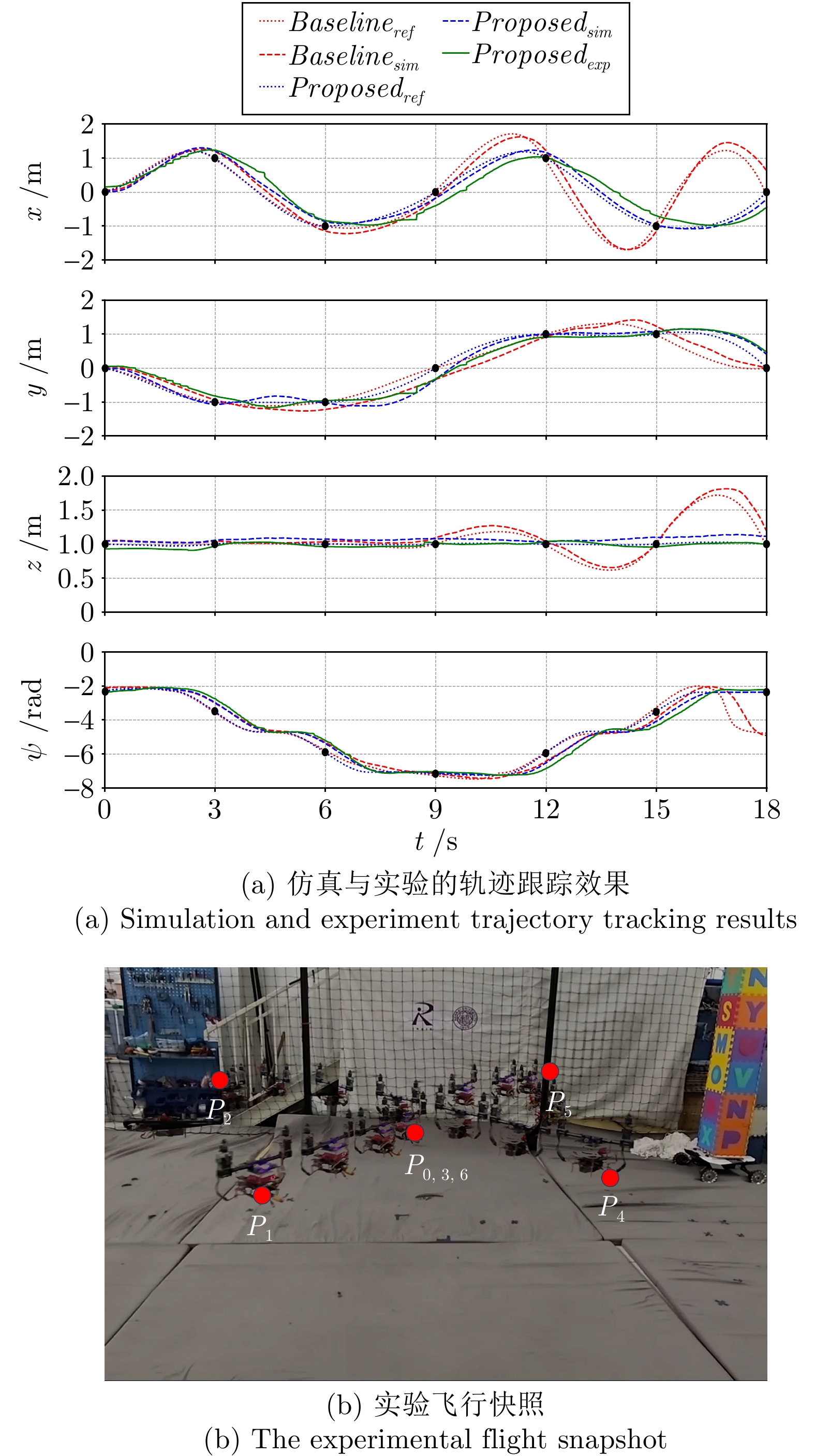
Table 3 Waypoint coordinates and reference yaw angles of trajectory 2

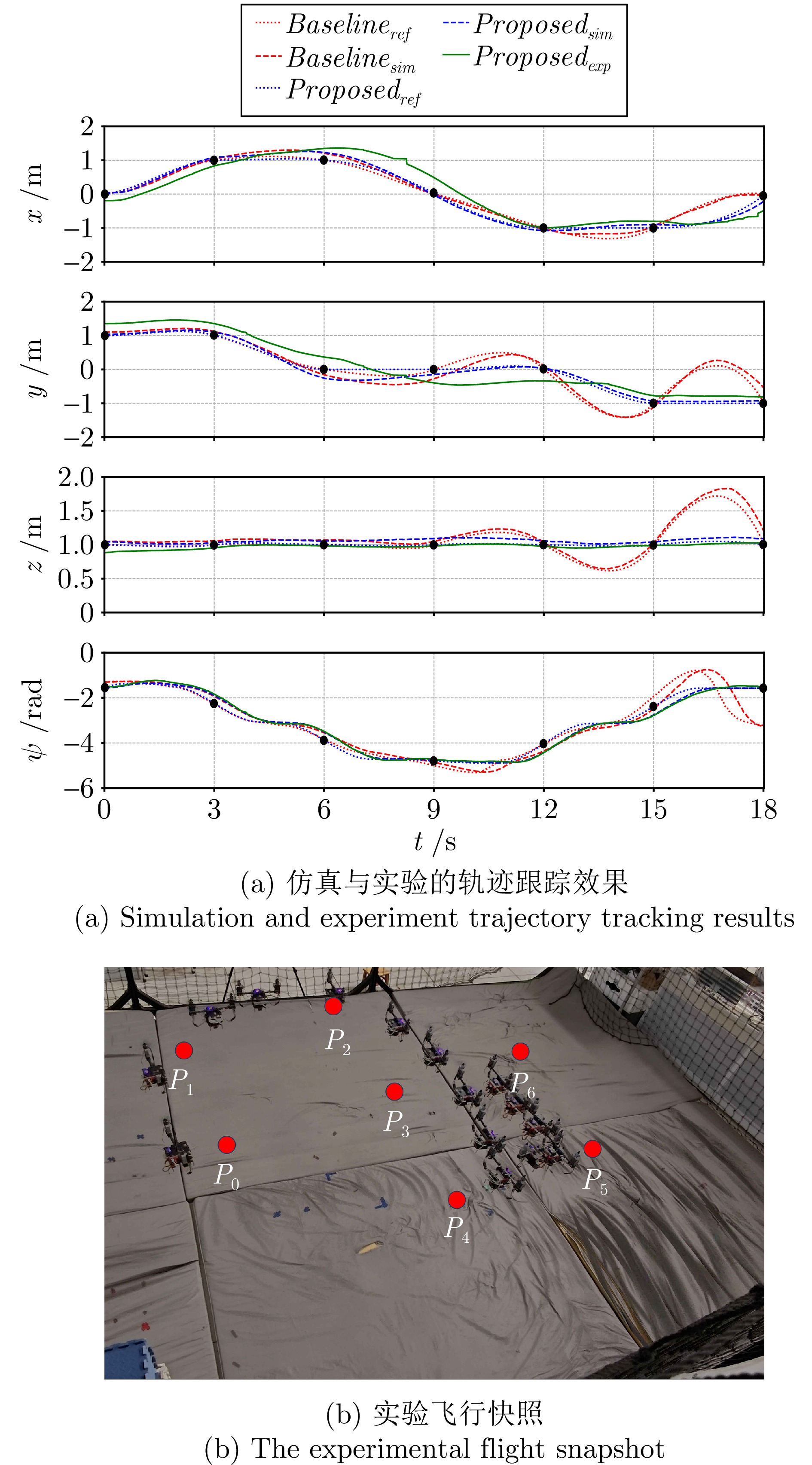
航点	时间$ t $ (s)	$ x $ (m)	$ y $ (m)	$ z $ (m)	$ \psi_{\rm{ref}} $ (rad)
$ P_0 $	0	$ \phantom{-}0.0 $	$ \phantom{-}1.0 $	$ 1.0 $	$ -0.50\pi $
$ P_1 $	3	$ \phantom{-}1.0 $	$ \phantom{-}1.0 $	$ 1.0 $	$ -1.00\pi $
$ P_2 $	6	$ \phantom{-}1.0 $	$ \phantom{-}0.0 $	$ 1.0 $	$ -1.50\pi $
$ P_3 $	9	$ \phantom{-}0.0 $	$ \phantom{-}0.0 $	$ 1.0 $	$ -1.50\pi $
$ P_4 $	12	$ -1.0 $	$ \phantom{-}0.0 $	$ 1.0 $	$ -1.00\pi $
$ P_5 $	15	$ -1.0 $	$ -1.0 $	$ 1.0 $	$ -0.50\pi $
$ P_6 $	18	$ \phantom{-}0.0 $	$ -1.0 $	$ 1.0 $	$ -0.50\pi $

下载: 导出CSV

表 4 轨迹三航点坐标及参考偏航角

Table 4 Waypoint coordinates and reference yaw angles of trajectory 3

航点	时间$ t $ (s)	$ x $ (m)	$ y $ (m)	$ z $ (m)	$ \psi_{\rm{ref}} $ (rad)
$ P_0 $	0	$ \phantom{-}0.0 $	$ \phantom{-}0.0 $	$ 1.0 $	$ -0.75\pi $
$ P_1 $	3	$ \phantom{-}1.0 $	$ -1.0 $	$ 1.0 $	$ -1.50\pi $
$ P_2 $	6	$ -1.0 $	$ -1.0 $	$ 1.0 $	$ -2.25\pi $
$ P_3 $	9	$ \phantom{-}0.0 $	$ \phantom{-}0.0 $	$ 1.0 $	$ -2.25\pi $
$ P_4 $	12	$ \phantom{-}1.0 $	$ \phantom{-}1.0 $	$ 1.0 $	$ -1.50\pi $
$ P_5 $	15	$ -1.0 $	$ \phantom{-}1.0 $	$ 1.0 $	$ -0.75\pi $
$ P_6 $	18	$ \phantom{-}0.0 $	$ \phantom{-}0.0 $	$ 1.0 $	$ -0.75\pi $

下载: 导出CSV

表 5 场景一航点坐标及参考偏航角

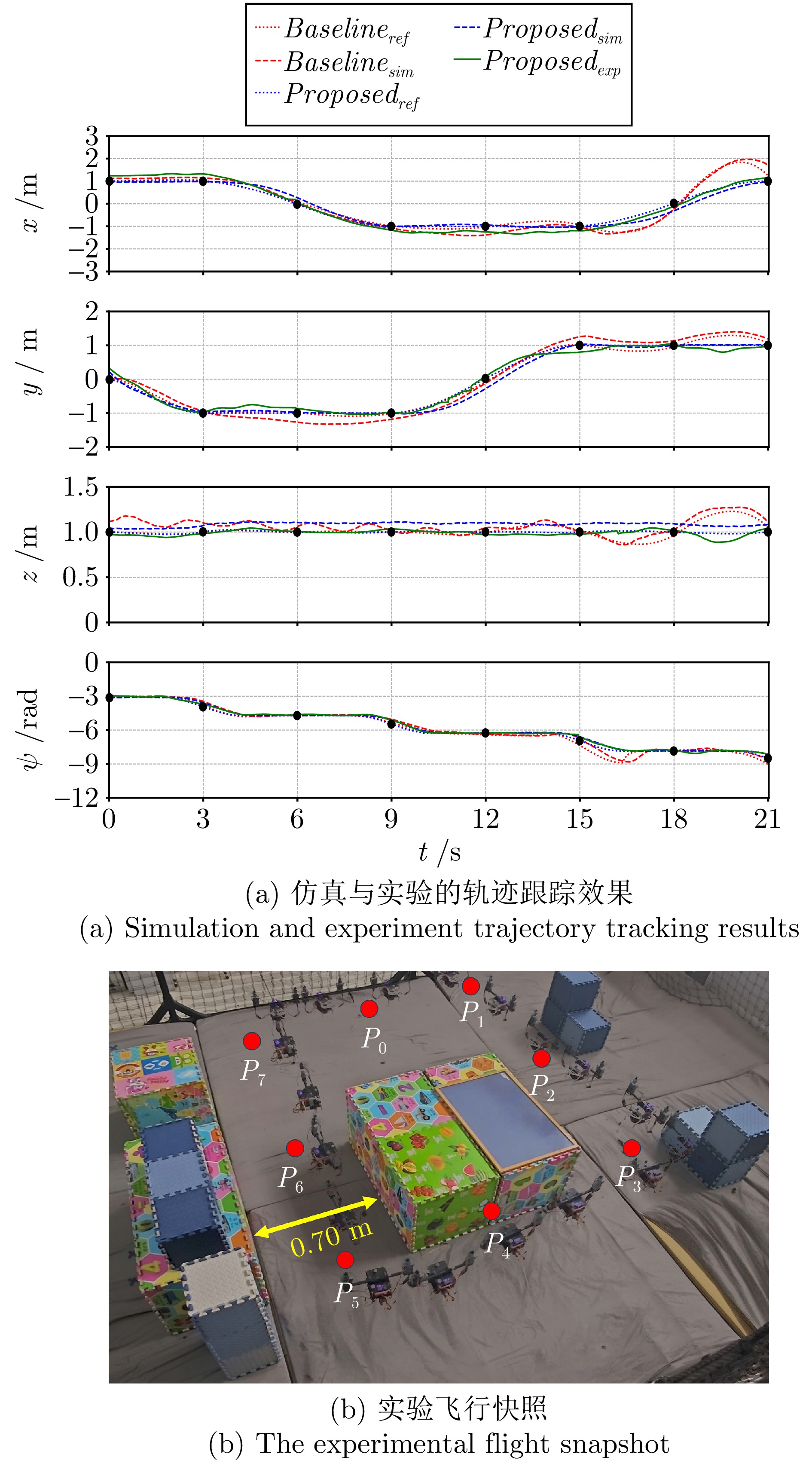
Table 5 Waypoint coordinates and reference yaw angle of scene 1

航点	时间$ t $ (s)	$ x $ (m)	$ y $ (m)	$ z $ (m)	$ \psi_{\rm{ref}} $ (rad)
$ P_0 $	0	$ \phantom{-}1.0 $	$ \phantom{-}0.0 $	$ 1.0 $	$ -1.00\pi $
$ P_1 $	3	$ \phantom{-}1.0 $	$ -1.0 $	$ 1.0 $	$ -1.50\pi $
$ P_2 $	6	$ \phantom{-}0.0 $	$ -1.0 $	$ 1.0 $	$ -1.50\pi $
$ P_3 $	9	$ -1.0 $	$ -1.0 $	$ 1.0 $	$ -2.00\pi $
$ P_4 $	12	$ -1.0 $	$ \phantom{-}0.0 $	$ 1.0 $	$ -2.00\pi $
$ P_5 $	15	$ -1.0 $	$ \phantom{-}1.0 $	$ 1.0 $	$ -2.50\pi $
$ P_6 $	18	$ \phantom{-}0.0 $	$ \phantom{-}1.0 $	$ 1.0 $	$ -2.50\pi $
$ P_7 $	21	$ \phantom{-}1.0 $	$ \phantom{-}1.0 $	$ 1.0 $	$ -3.00\pi $

下载: 导出CSV

表 6 场景二航点坐标及参考偏航角

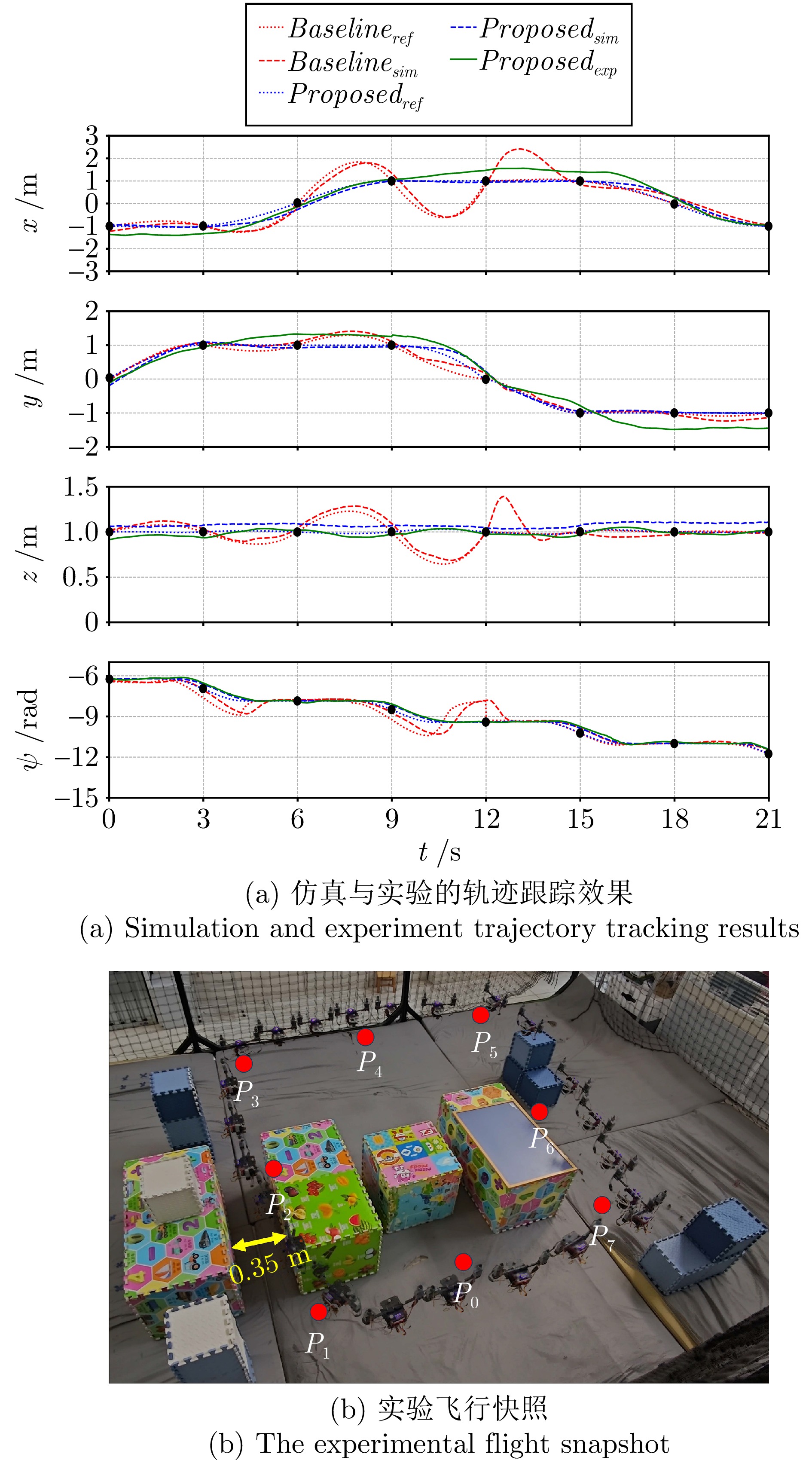
Table 6 Waypoint coordinates and reference yaw angle of scene 2

航点	时间$ t $ (s)	$ x $ (m)	$ y $ (m)	$ z $ (m)	$ \psi_{\rm{ref}} $ (rad)
$ P_0 $	0	$ -1.0 $	$ \phantom{-}0.0 $	$ 1.0 $	$ -2.00\pi $
$ P_1 $	3	$ -1.0 $	$ \phantom{-}1.0 $	$ 1.0 $	$ -2.50\pi $
$ P_2 $	6	$ \phantom{-}0.0 $	$ \phantom{-}1.0 $	$ 1.0 $	$ -2.50\pi $
$ P_3 $	9	$ \phantom{-}1.0 $	$ \phantom{-}1.0 $	$ 1.0 $	$ -3.00\pi $
$ P_4 $	12	$ \phantom{-}1.0 $	$ \phantom{-}0.0 $	$ 1.0 $	$ -3.00\pi $
$ P_5 $	15	$ \phantom{-}1.0 $	$ -1.0 $	$ 1.0 $	$ -3.50\pi $
$ P_6 $	18	$ \phantom{-}0.0 $	$ -1.0 $	$ 1.0 $	$ -3.50\pi $
$ P_7 $	21	$ -1.0 $	$ -1.0 $	$ 1.0 $	$ -4.00\pi $

下载: 导出CSV

表 7 引入偏航方向约束前后轨迹质量指标对比

Table 7 Comparison of trajectory quality metrics with and without yaw direction constraints

轨迹/ 场景	方法	$ a_{{\rm{rms}}} ({\rm{m/s}}^2) $	$ \dot{\psi}_{{\rm{rms}}} ({\rm{rad/s}}) $	$ \eta_e $
轨迹一	对比方法	1.15	0.07	3.06
轨迹一	所提方法	0.96	0.01	1.10
轨迹二	对比方法	1.18	0.02	1.65
轨迹二	所提方法	0.55	0.01	1.03
轨迹三	对比方法	6.62	0.03	1.63
轨迹三	所提方法	3.82	0.02	1.09
场景一	对比方法	0.95	0.02	1.37
场景一	所提方法	0.35	0.01	1.01
场景二	对比方法	5.34	0.05	1.76
场景二	所提方法	1.49	0.01	1.00

下载: 导出CSV

参考文献(27)

[1]	Li W Q, Han X X, Lin Z B, Rahman A. Enhanced pest and disease detection in agriculture using deep learning-enabled drones. Acadlore Transactions on AI and Machine Learning, 2024, 3(1): 1−10 doi: 10.56578/ataiml030101
[2]	Liu B, Ni W, Liu R P, Guo Y J, Zhu H. Optimal routing of unmanned aerial vehicle for joint goods delivery and in-situ sensing. IEEE Transactions on Intelligent Transportation Systems, 2022, 24(3): 3594−3599 doi: 10.1109/tits.2022.3225269
[3]	Abdellatif A A, Elmancy A, Mohamed A, Massoud A, Lebda W, Naji K K. PDSR: Efficient uav deployment for swift and accurate post-disaster search and rescue. IEEE Internet of Things Magazine, 2025, 8(3): 149−156 doi: 10.1109/IOTM.001.2400139
[4]	刘彦伟, 潘豪, 刘三娃, 李淑娟, 李言. 倾转变形四旋翼飞行器的设计和实现. 中国机械工程, 2021, 32(16): 1930−1936 doi: 10.3969/j.issn.1004-132X.2021.16.005 Liu Yan-Wei, Pan Hao, Liu San-Wa, Li Shu-Juan, Li Yan. Design and implementation of a tilt-deformable quadrotor. China Mechanical Engineering, 2021, 32(16): 1930−1936 doi: 10.3969/j.issn.1004-132X.2021.16.005
[5]	Xu M, De Q, Yu D, Hu A, Liu Z, Wang H. Biomimetic morphing quadrotor inspired by eagle claw for dynamic grasping. IEEE Transactions on Robotics, 2024, 40: 2513−2528 doi: 10.1109/TRO.2024.3386616
[6]	Hameed S W, Jie A L J, Imanberdiyev N, Camci E, Yau W, Feroskhan M. Dragonfly drone: A novel tilt-rotor aerial platform with body-morphing capability. In: Proceedings of the 2025 International Conference on Robotics and Automation. Atlanta, USA: IEEE, 2025. 8642-8648
[7]	Chen S, Li Y, Lou Y, Lin K, Wu X. Learning real-time dynamic responsive gap-traversing policy for quadrotors with safety-aware exploration. IEEE Transactions on Intelligent Vehicles, 2022, 8(3): 2271−2284 doi: 10.1109/tiv.2022.3229723
[8]	Song Y, Romero A, Müller M, Koltun V, Scaramuzza D. Reaching the limit in autonomous racing: Optimal control versus reinforcement learning. Science Robotics, 2023, 8(82): Article No.eadg1462 doi: 10.1126/scirobotics.adg1462
[9]	Wang M, Wang Q, Wang Z, Gao Y, Wang J, Cui C, et al. Unlocking aerobatic potential of quadcopters: Autonomous freestyle flight generation and execution. Science Robotics, 2025, 10(101): Article No.eadp9905 doi: 10.1126/scirobotics.adp9905
[10]	Qin Y, Xu W, Lee A, Zhang F. Gemini: A compact yet efficient bi-copter UAV for indoor applications. IEEE Robotics and Automation Letters, 2020, 5(2): 3213−3220 doi: 10.1109/lra.2020.2974718
[11]	林惠韩, 冯令兵, 冯卓, 赵宸玥, 赵良宇. 圆柱形定桨距共轴双旋翼无人机的制导控制系统设计. 航空兵器, 2023, 30(5): 42−49 doi: 10.12132/ISSN.1673-5048.2023.0047 Lin Hui-han, Feng Ling-bing, Feng Zhuo, Zhao Chen-yue, Zhao Liang-yu. Design of guidance and control system for cylindrical fixed-pitch coaxial twin-rotor unmanned aerial vehicle. Aero Weaponry, 2023, 30(5): 42−49 doi: 10.12132/ISSN.1673-5048.2023.0047
[12]	Chen L, Xiao J, Zheng Y, Alagappan N A, Feroskhan M. Design, modeling, and control of a coaxial drone. IEEE Transactions on Robotics, 2024, 40: 1650−1663 doi: 10.1109/TRO.2024.3354161
[13]	李隆, 李勃达, 孙海龙, 郭颜东, 曹建波, 何柏岩. 基于双环PID的共轴双旋翼舵机控制算法优化. 科学技术与工程, 2025, 25(21): 9166−9172 doi: 10.12404/j.issn.1671-1815.2404948 Li Long, Li Bo-da, Sun Hai-long, Guo Yan-dong, Cao Jian-bo, He Bai-yan. Optimization of coaxial dual-rotor servo control algorithm based on dual-loop PID. Science Technology and Engineering, 2025, 25(21): 9166−9172 doi: 10.12404/j.issn.1671-1815.2404948
[14]	Zhang Q, Liu Z, Zhao J, Zhang S. Modeling and attitude control of bi-copter. In: Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems. Beijing, China: IEEE, 2016. 172-176
[15]	Li Y, Qin Y, Xu W, Zhang F. Modeling, identification, and control of non-minimum phase dynamics of bi-copter UAVs. In: Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Boston, USA: IEEE, 2020. 1249-1255
[16]	Qin Y, Chen N, Cai Y, Xu W, Zhang F. Gemini II: Design, modeling, and control of a compact yet efficient servoless bi-copter. IEEE/ASME Transactions on Mechatronics, 2022, 27(6): 4304−4315 doi: 10.1109/TMECH.2022.3153587
[17]	Lu J, Zhang X, Shen H, Xu L, Tian B. You only plan once: A learning-based one-stage planner with guidance learning. IEEE Robotics and Automation Letters, 2024, 9(7): 6083−6090 doi: 10.1109/LRA.2024.3399589
[18]	李俊志, 龙腾, 孙景亮, 苗洪语, 周桢林. 城市环境下固定翼无人机微分平坦时空分层轨迹规划. 航空学报, 2025, 46(11): 204−219 doi: 10.7527/S1000-6893.2024.31369 Li Jun-zhi, Long Teng, Sun Jing-liang, Miao Hong-yu, Zhou Zhen-lin. Differential flatness-based spatial-temporal hierarchical trajectory planning for fixed-wing UAVs in urban environments. Acta Aeronautica et Astronautica Sinica, 2025, 46(11): 204−219 doi: 10.7527/S1000-6893.2024.31369
[19]	肖丽丽, 蒋海波. 基于改进的水鹰优化算法的空中无人机三维避障策略. 软件工程, 2025, 28(08): 58−63 doi: 10.19644/j.cnki.issn2096-1472.2025.008.012 Xiao Li-li, Jiang Hai-bo. Three-dimensional obstacle avoidance strategy for aerial drones based on prompt water eagle optimization algorithm. Software Engineering, 2025, 28(08): 58−63 doi: 10.19644/j.cnki.issn2096-1472.2025.008.012
[20]	Sun W, Sun P, Ding W, Zhao J, Li Y. Gradient-based autonomous obstacle avoidance trajectory planning for B-spline UAVs. Scientific Reports, 2024, 14(1): Article No.14458 doi: 10.1038/s41598-024-65463-w
[21]	Chen H, Tao J, Zhou B, Liu X. Research on an autonomous UAV search and rescue system based on the improved EGO-Planner algorithm. In: Proceedings of the 2024 IEEE International Conference on Computer Engineering and Application. Hangzhou, China: IEEE, 2024. 1170-1175
[22]	Wang Z, Zhou X, Xu C, Gao F. Geometrically constrained trajectory optimization for multicopters. IEEE Transactions on Robotics, 2022, 38(5): 3259−3278 doi: 10.1109/TRO.2022.3160022
[23]	姬博洋, 李炯, 贺杨超, 叶继坤, 雷虎民. 基于最小代价准则的再入滑翔制导方法. 系统工程与电子技术, 2025, 47(8): 2715−2726 Ji Bo-yang, Li Jiong, He Yang-chao, Ye Ji-kun, Lei Hu-min. Reentry gliding vehicle guidance method based on min-cost criterion. Systems Engineering and Electronics, 2025, 47(8): 2715−2726
[24]	雷刚, 王和, 李少朋, 罗炜. 考虑路径点约束的攻击时间与攻击角度控制制导方法. 中国惯性技术学报, 2025, 33(2): 172−178 doi: 10.13695/j.cnki.12-1222/o3.2025.02.009 Lei Gang, Wang He, Li Shao-peng, Luo Wei. Impact time and angle control guidance method with way-pointconstraint. Journal of Chinese Inertial Technology, 2025, 33(2): 172−178 doi: 10.13695/j.cnki.12-1222/o3.2025.02.009
[25]	He X, Wang Y. Design and trajectory tracking control of a new bi-copter UAV. IEEE Robotics and Automation Letters, 2022, 7(4): 9191−9198 doi: 10.1109/LRA.2022.3190090
[26]	Mellinger D, Kumar V. Minimum snap trajectory generation and control for quadrotors. In: Proceedings of the 2011 IEEE International Conference on Robotics and Automation. Shanghai, China: IEEE, 2011. 2520-2525
[27]	Hao Z, Cai Z. Control of a Bi-copter UAV subject to model uncertainties. International Conference on Guidance, Navigation and Control. Singapore: Springer Nature Singapore, 2024. 261−269