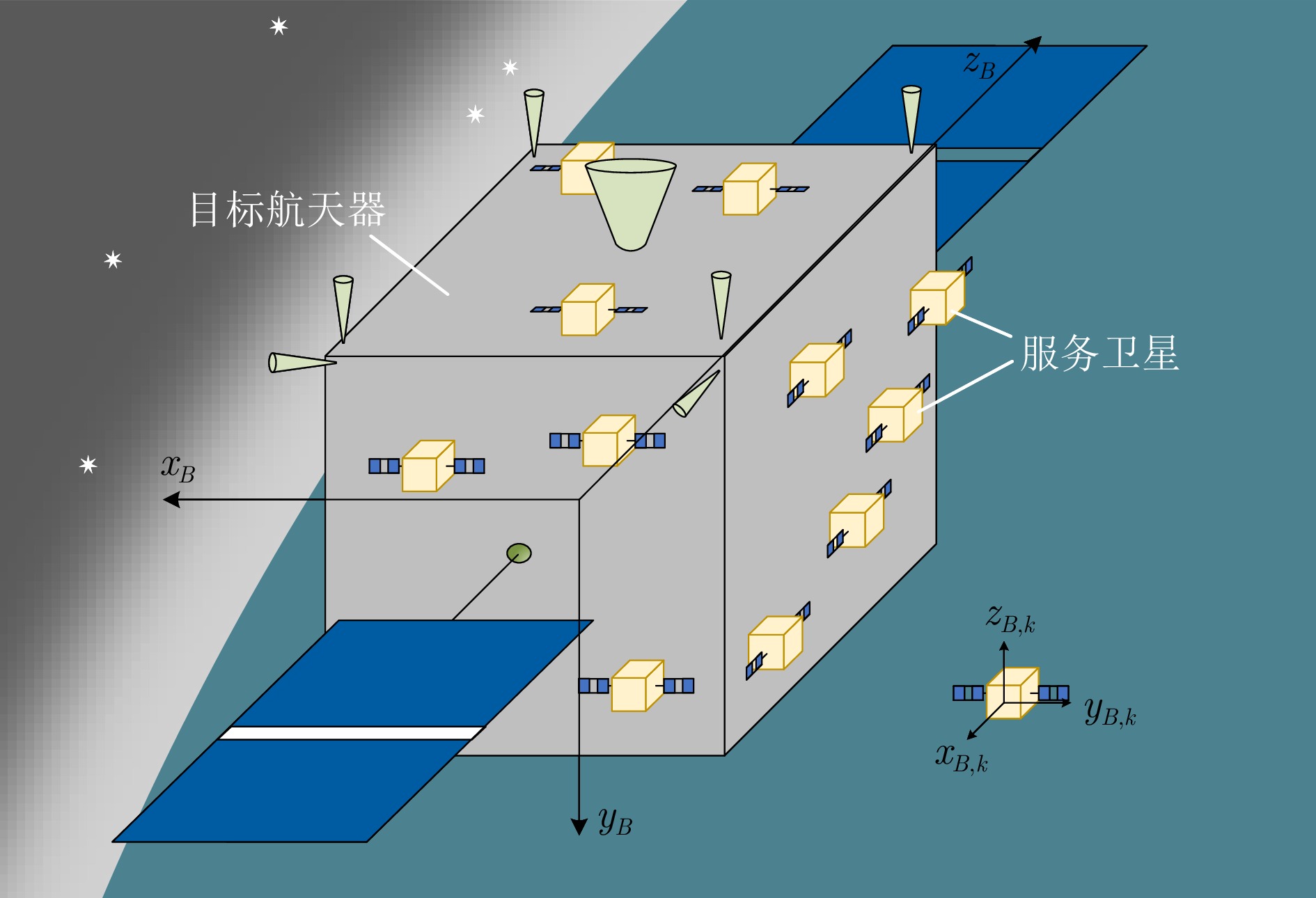
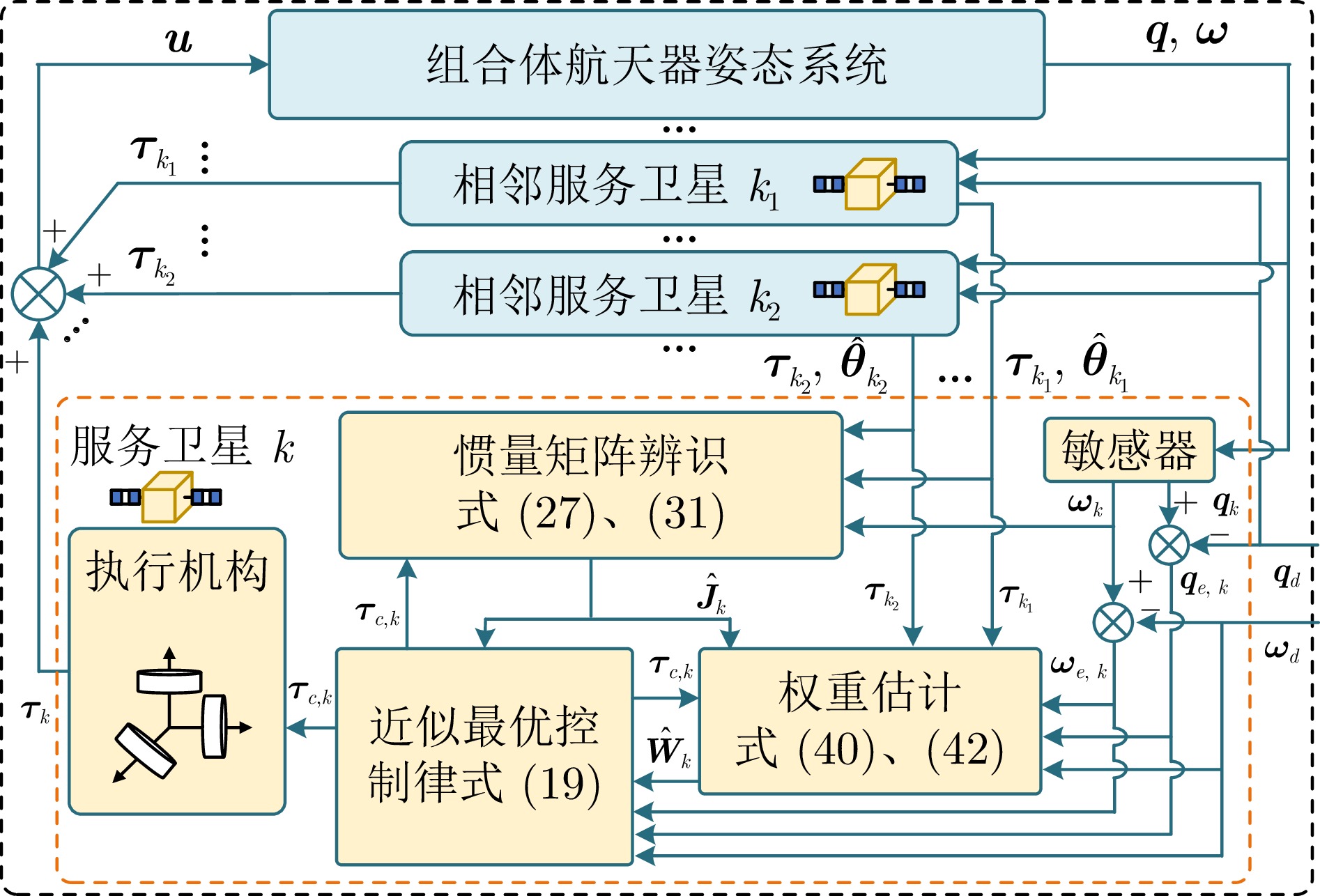
Distributed Approximate Optimal Attitude Tracking Control for Taking-over the Target by Multiple Satellites
-
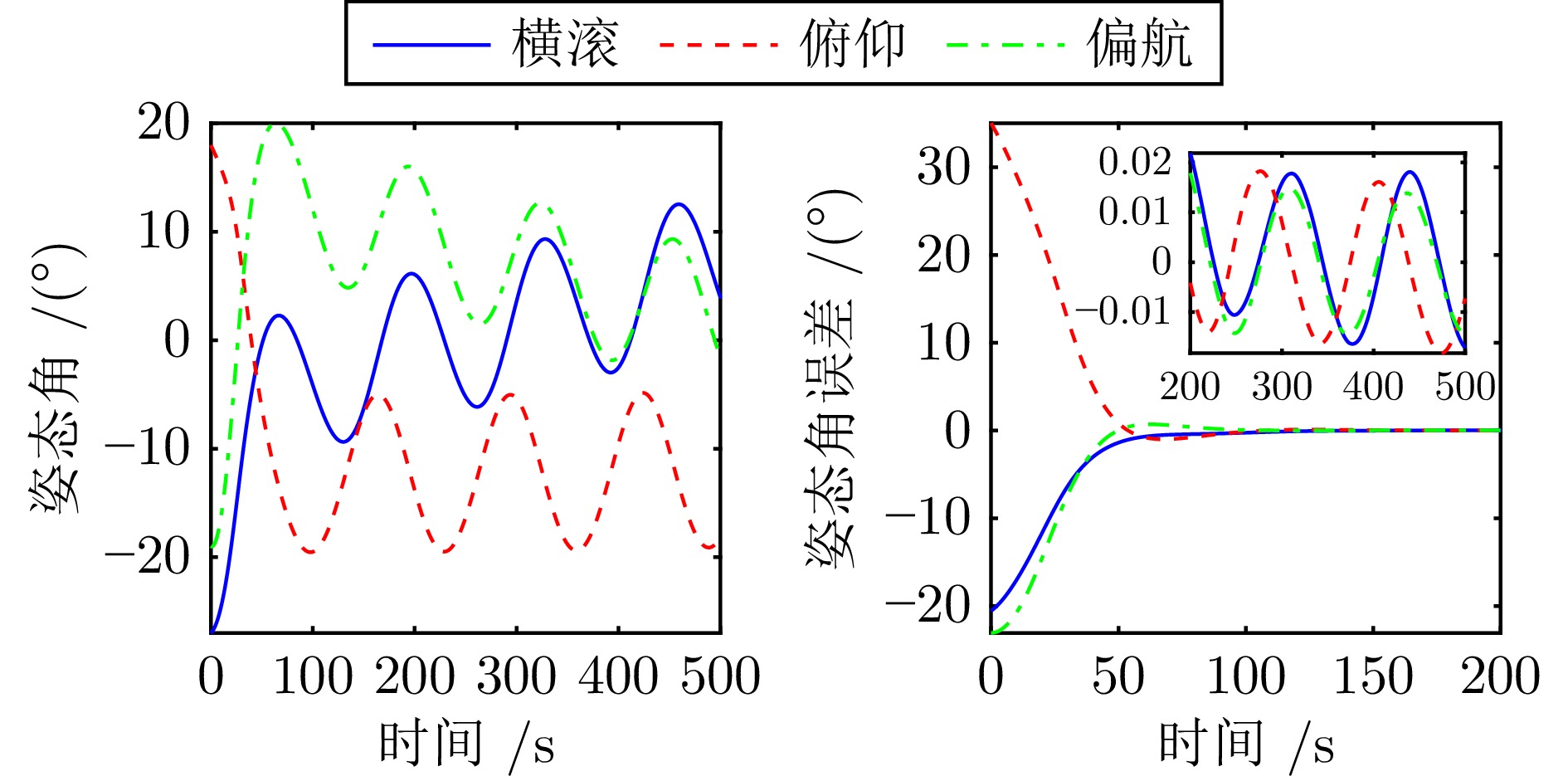
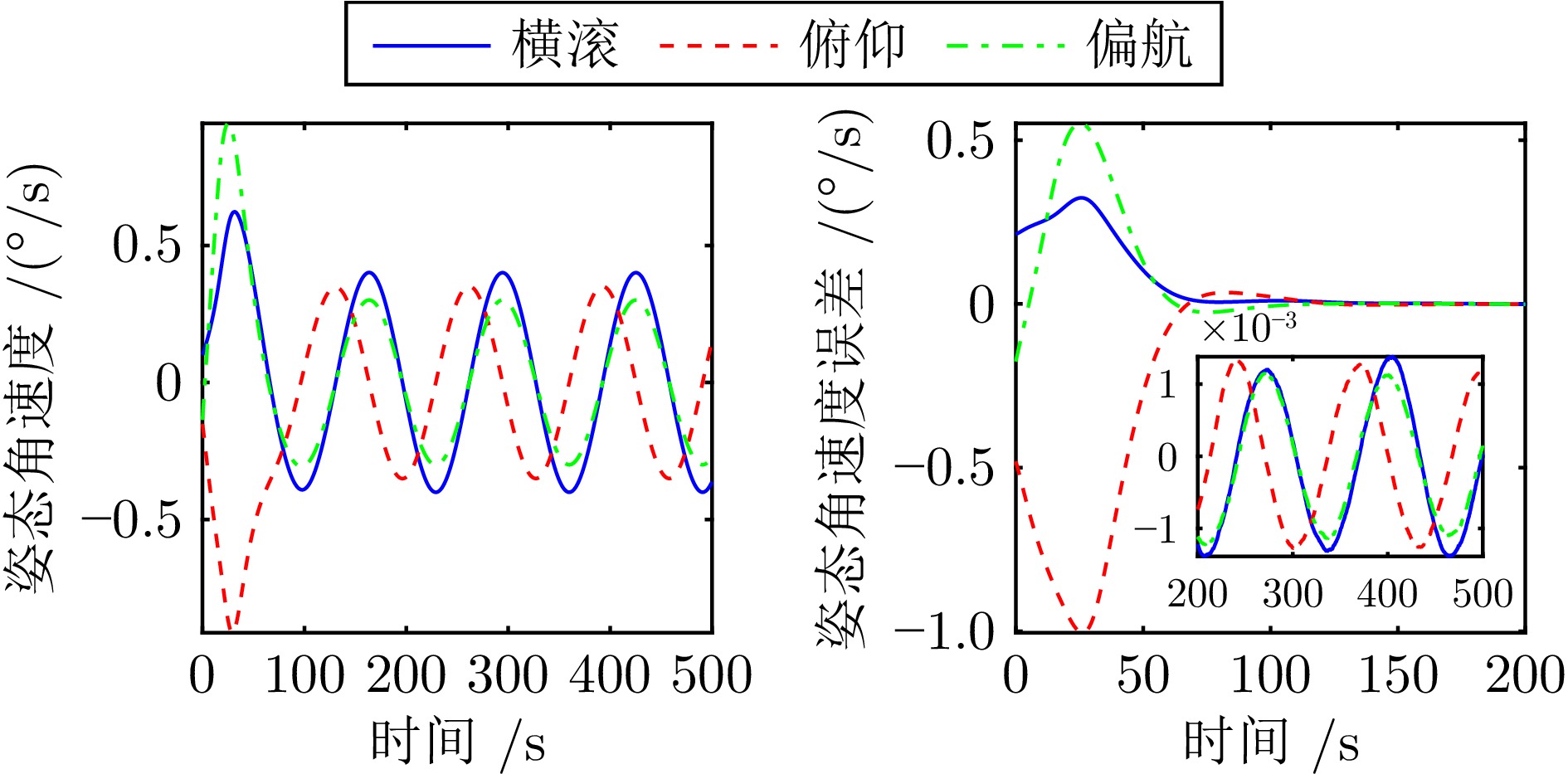
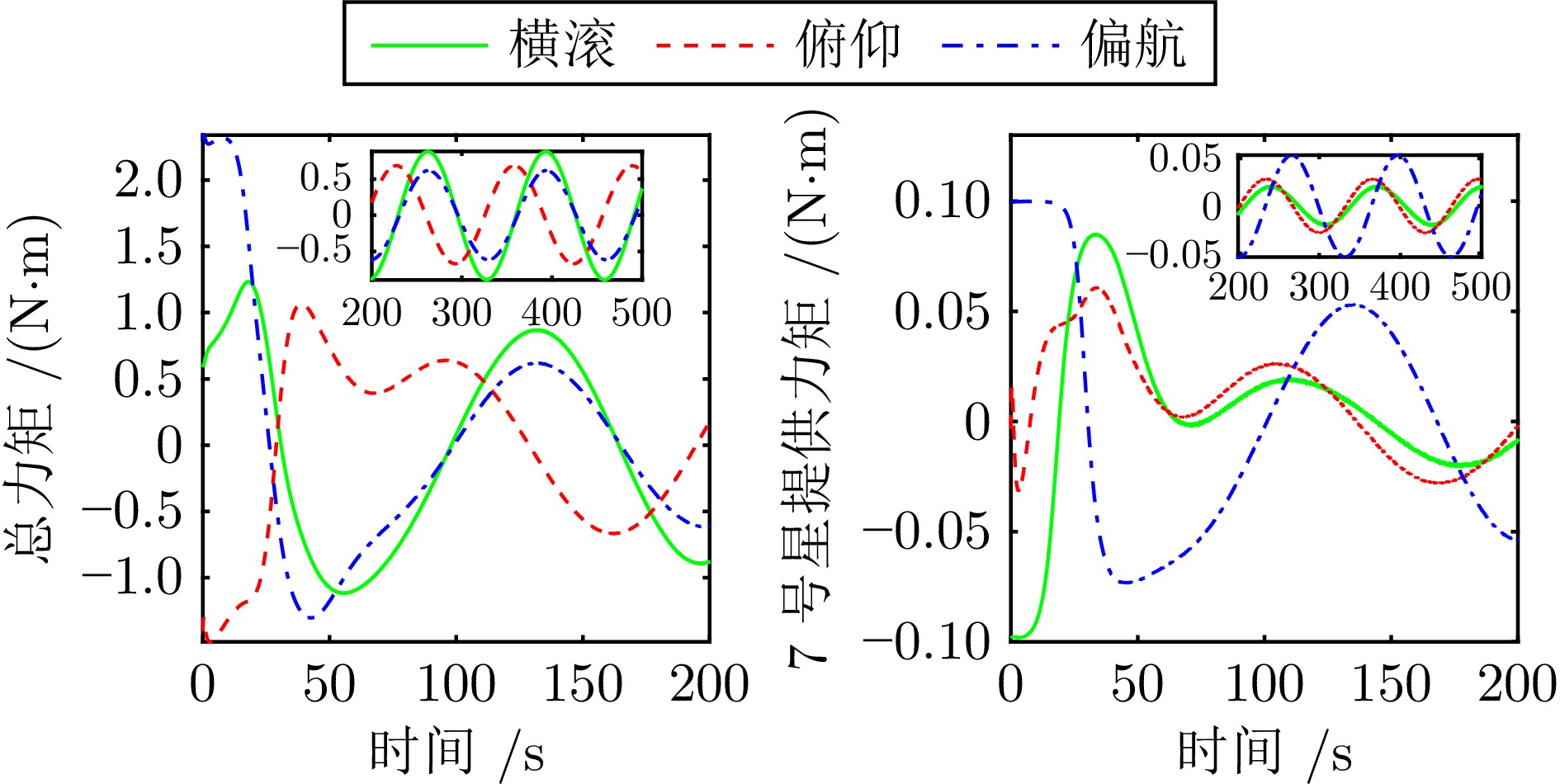
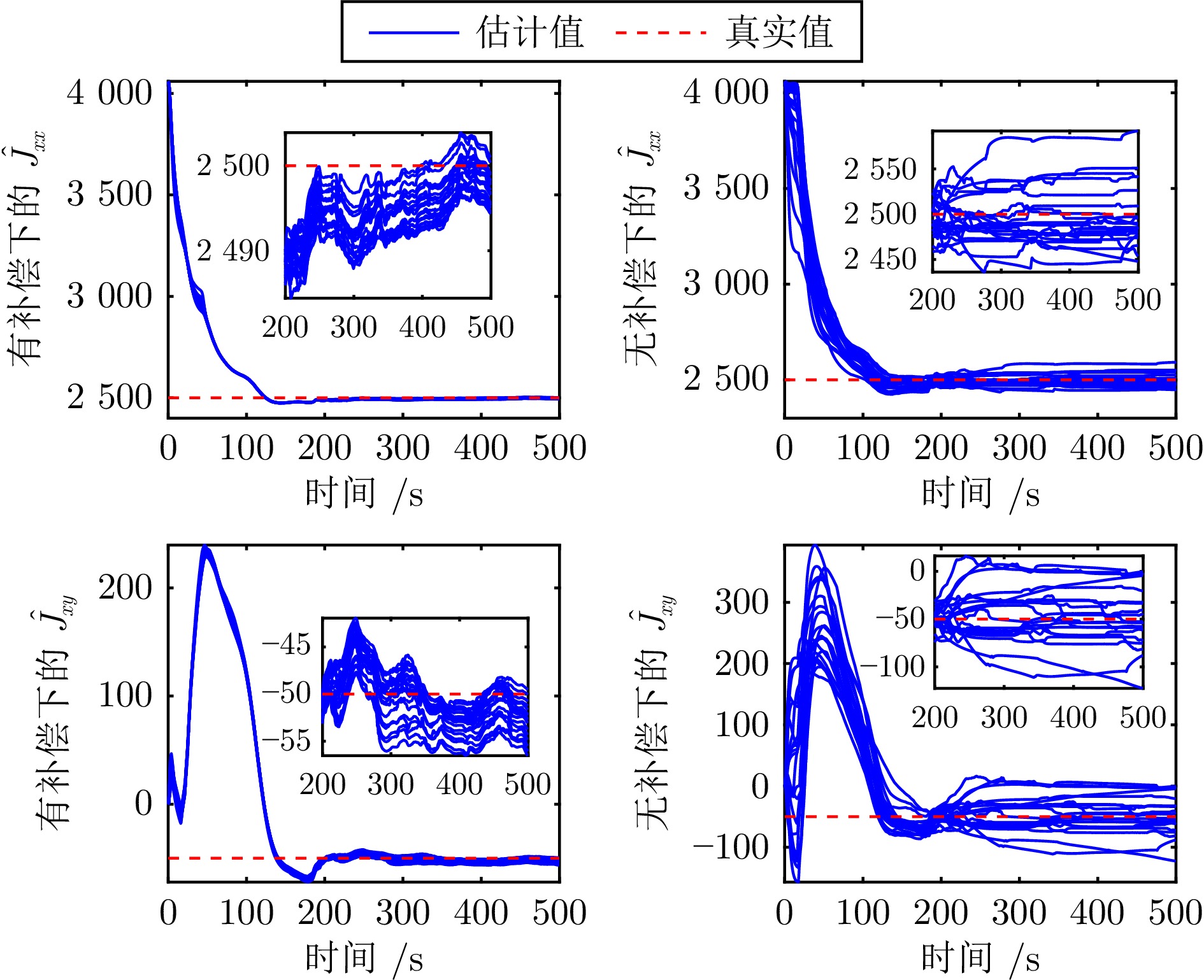
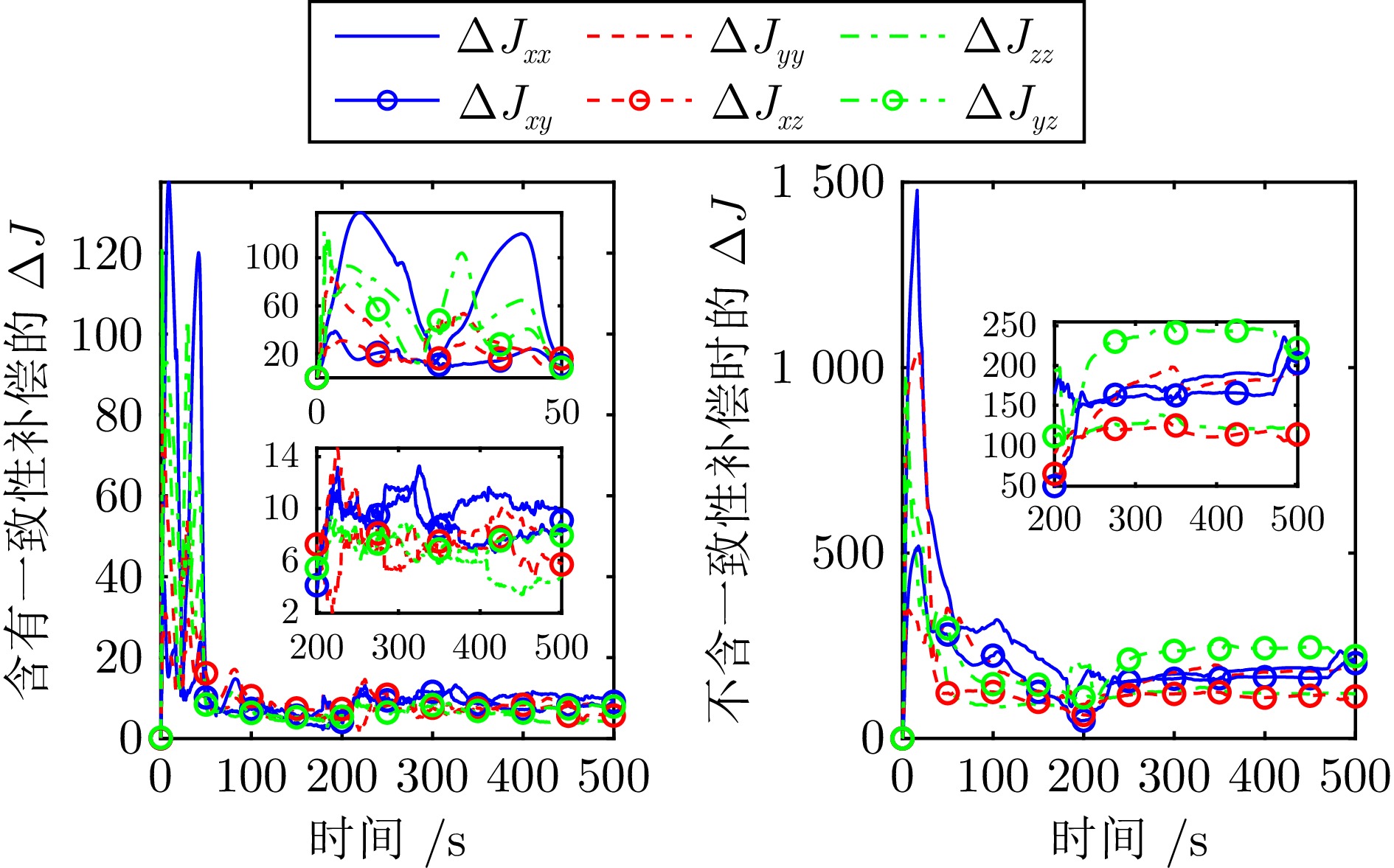
摘要: 在多服务星对失效航天器进行姿态接管控制的在轨服务任务中, 考虑惯量矩阵未知和执行机构饱和的情况, 基于自适应动态规划(ADP)方法提出一种分布式姿态跟踪接管控制策略. 首先, 通过对姿态系统的建模分析, 设计一种含有力矩饱和约束和期望力矩补偿的值函数, 在ADP框架下, 用一组基函数逼近最优值函数, 并得到分布式近似最优姿态跟踪控制策略; 然后, 为避免使用角加速度信息, 分别构建关于惯量参数和权重参数的滤波形式的线性回归模型, 根据并行学习方法、参数一致性算法和离线策略轨迹, 设计惯量参数自适应辨识律和权重更新律; 接着使用李雅普诺夫方法证明姿态跟踪误差、惯量矩阵辨识误差和权重参数估计误差的一致最终有界; 最后, 仿真结果验证了分布式跟踪控制方法在力矩饱和约束下对姿态跟踪和惯量矩阵辨识的有效性.Abstract: In the on-orbit service missions of attitude takeover control of the failed spacecraft by multiple service satellites, a distributed attitude tracking takeover control policy is proposed based on the method of adaptive dynamic programming (ADP) with unknown inertia matrix and actuator saturation. Firstly, by modeling and analyzing the attitude system, a value function with torque saturation constraint and desired torque compensation is designed. Under the ADP framework, a set of basis functions is used to approximate the optimal value function, and the distributed approximate optimal attitude tracking control strategy is obtained; Then, the filtered linear regression models relevant to inertia parameters and weight parameters are respectively established with angular acceleration information free and according to concurrent learning method, parameter consensus algorithm and off-policy trajectories, the adaptive inertia parameter identification law and the weight update law are designed; Furthermore, the uniformly ultimate boundedness of the attitude tracking errors, the inertia matrix identification errors and weight estimation errors are proved by Lyapunov method; Finally, the simulation results verify the effectiveness of the distributed attitude tracking control method for attitude tracking and inertia matrix identification under the constraint of torque saturation.
-
图 3 分布式姿态接管控制系统框图
Fig. 3 The diagram of the distributed attitude takeover control system
图 7 总力矩及7号服务卫星提供的分力矩曲线
Fig. 7 Curves of total torques and divided torques provided by service satellite 7
图 8 惯量参数估计值及其误差曲线
Fig. 8 Curves of estimates of the inertia parameters and their errors
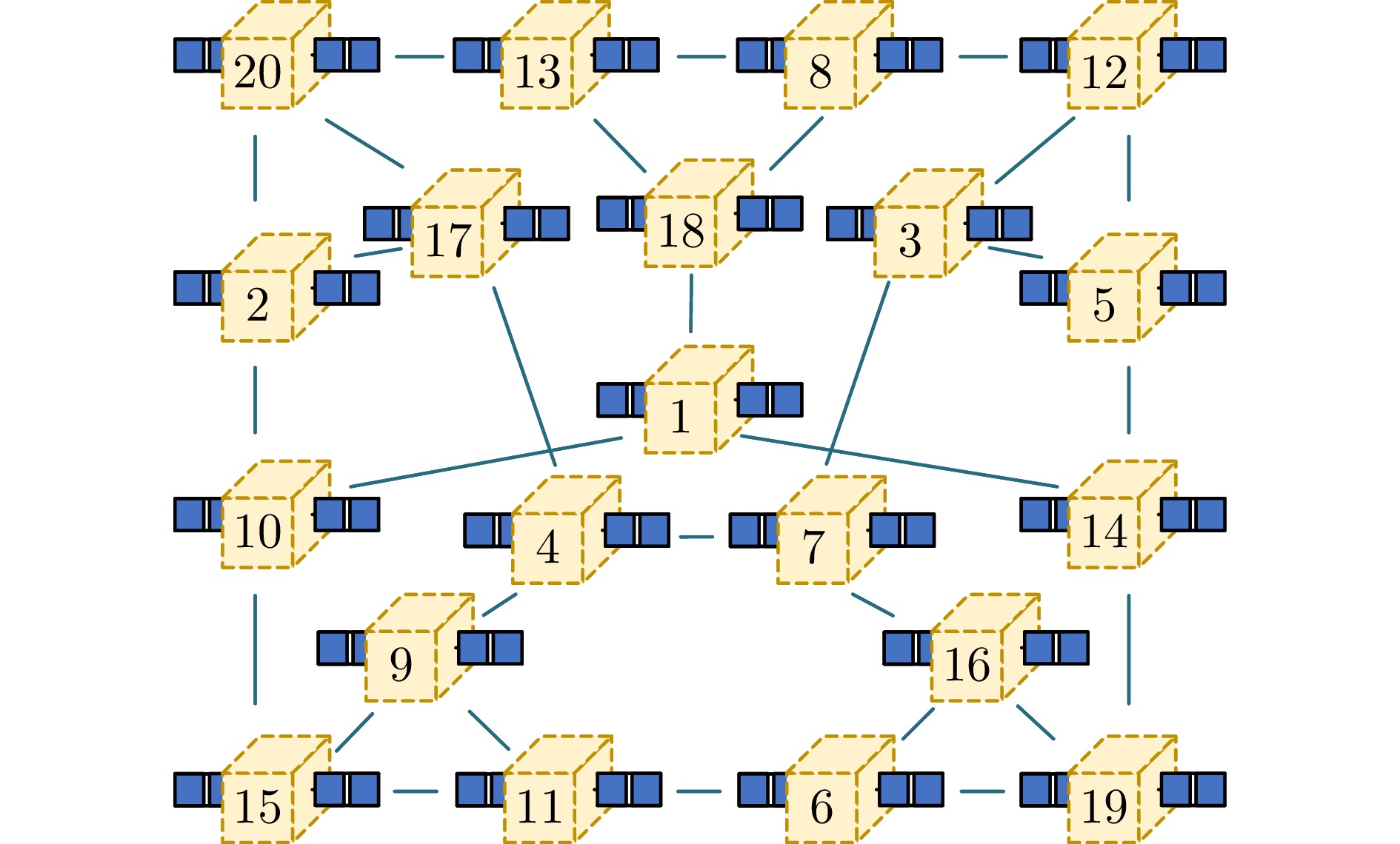
表 1 服务卫星相对姿态角的真值
Table 1 True values of relative attitude angles of service satellites
$ k $ 相对姿态角$ {{ \boldsymbol{\alpha }_{B}^{k}}}\,\; (^\circ) $ $ k $ 相对姿态角$ {{ \boldsymbol{\alpha }_{B}^{k}}}\,\; (^\circ) $ $ 1 $ $ \left[ {0,\;0,\;0 } \right] $ $ 11 $ $ \left[ {53,\;10,\;11 } \right] $ $ 2 $ $ \left[ {-20,\;35,\;160} \right] $ $ 12 $ $ \left[ {63,\;15,\;80 } \right] $ $ 3 $ $ \left[ {75,\;16,\;93 } \right] $ $ 13 $ $ \left[ {-83,\;-77,\;168} \right] $ $ 4 $ $ \left[ {-108,\;61,\;-5} \right] $ $ 14 $ $ \left[ {-84,\;-48,\;16 } \right] $ $ 5 $ $ \left[ {-173,\;8,\;15 } \right] $ $ 15 $ $ \left[ {37,\;-3,\;-101 } \right] $ $ 6 $ $ \left[ {117,\;83,\;163} \right] $ $ 16 $ $ \left[ {137,\;83,\;-173} \right] $ $ 7 $ $ \left[ {23,\;46,\;12 } \right] $ $ 17 $ $ \left[ {118,\;3,\;-157 } \right] $ $ 8 $ $ \left[ {60,\;73,\;166 } \right] $ $ 18 $ $ \left[ {-86,\;78,\;-169} \right] $ $ 9 $ $ \left[ {133,\;-16,\;84} \right] $ $ 19 $ $ \left[ {43,\;78,\;11 } \right] $ $ 10 $ $ \left[{162,\;54,\;13 } \right] $ $ 20 $ $ \left[ {77,\;12,\;180 } \right] $ 
下载: 导出CSV
表 2 姿态控制仿真参数
Table 2 Parameters of attitude control simulation
参数 数值 姿态初值 $ {{\boldsymbol{q}}}(0)={{\left[0.953\,\;3\,\;-0.202\,\;3\,\;0.188\,\;1\,\; -0.122\,\;5 \right]}^{\text{T}}} $ 角速度初值 $ \boldsymbol{\omega }(0)={{\left[ 0.1\,\;-1.5\,\;-0.14 \right]}^{\text{T}}}\,\;{^\circ/\text{s}} $ 期望姿态初值 $ {{\boldsymbol{q}}_{d}}(0)={{\left[ 1\,\;0\,\; 0\,\;0 \right]}^{\text{T}}} $ 期望姿态角速度 $ {{\boldsymbol{\omega }}_{d}}(t)=\left[\begin{matrix} 0.4\sin \left( 0.048t \right)\\0.35\cos \left( 0.048t \right)\\0.3\sin \left( 0.048t \right) \end{matrix} \right]\,\;{^{\circ }}/{\text{s}} $ 执行机构最大力矩 $ {{\tau }_{\max }}=0.1 \,\;{\text{N}\cdot \text{m}} $ 值函数因子 $ {{Q}_{\omega }}=100 $, $ {{Q}_{q}}=100 $, $ {{Q}_{\tau }}=1 $ 惯量参数初值 $ \hat{\boldsymbol \theta} \left( 0 \right)=\left[ {4\,\;059\times{{\boldsymbol 1}_{1\times 3}}} \,\; {{\boldsymbol 0}_{1\times3}} \right]^{\text{T}} $ 惯量参数上限 $ \bar{\boldsymbol{\theta }}_k={{\left[ 5\,\;000 \,\; 5\,\;000 \,\; 5\,\;000\,\; 400\,\; 400\,\; 400\right]}^{\text{T}}} $ 惯量参数下限 $ \underline{\boldsymbol{\theta }}_k={{\left[ 1\,\;500\,\; 1\,\;500 \,\; 1\,\;500\,\; -400\,\; -400\,\; -400\right]}^{\text{T}}} $ 式(27)、(31)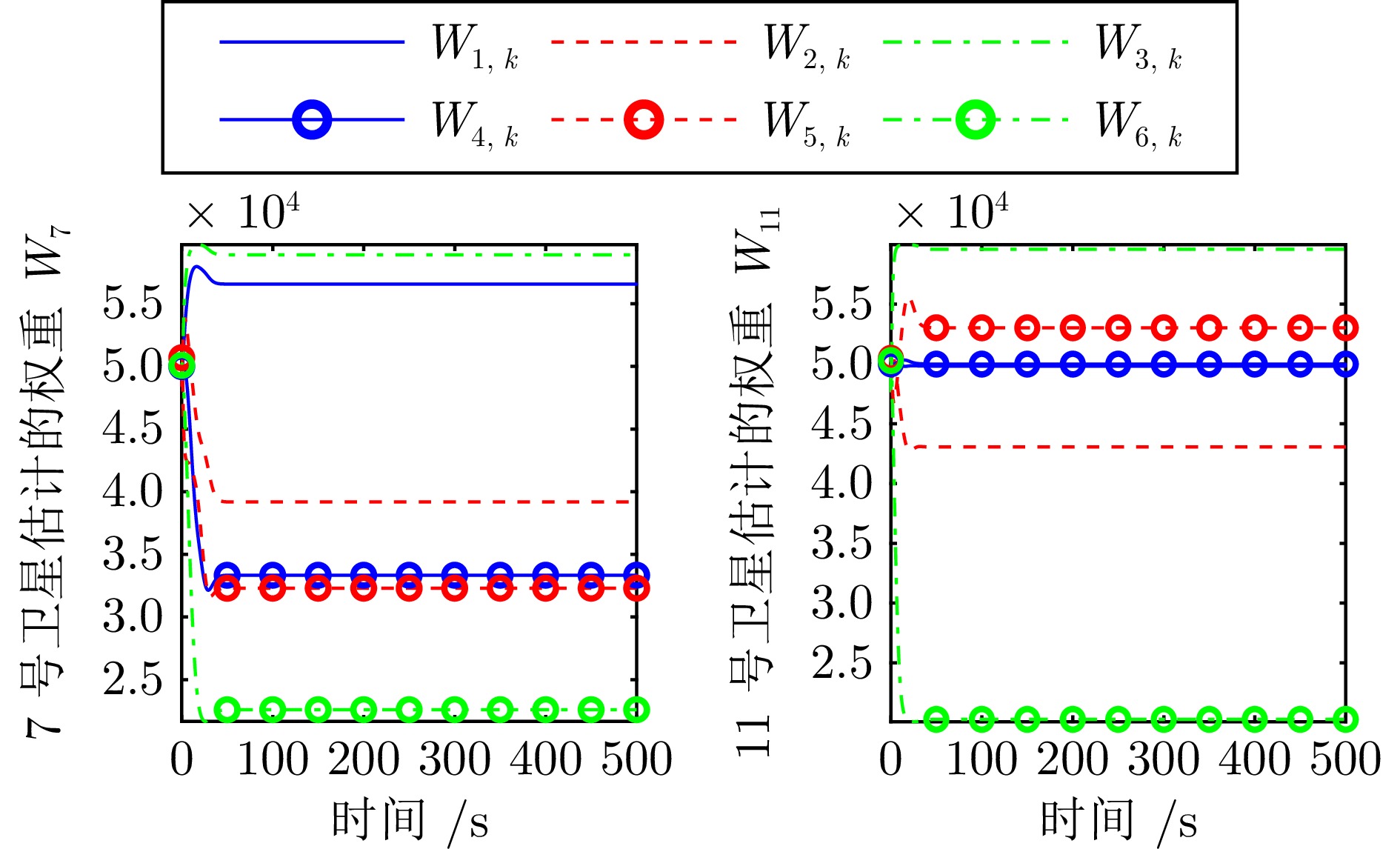的
参数$ \begin{array}{c} {{\bar{p}}_{\theta }}=30,\; {{\bar{\kappa }}_{\theta }}=10,\; {{\underline{\kappa }}_{\theta }}=0.4,\; {{K}_{\theta 1}}=20,\;\\{{K}_{\theta 2}}=1,\; {{K}_{\theta 3}}=0.004,\; {{\gamma }_{\theta 1}}=0.1,\; {{\gamma }_{\theta 2}}=0.1\end{array} $ 权重参数初值 $ \hat{\boldsymbol W} \left( 0 \right)=5\times{{10}^{4}}\times{{\boldsymbol 1}_{6\times 1}} $ 权重参数上限 $ {{\bar{\boldsymbol{W}}}_{k}}={{\left[ 6\times {{\boldsymbol 1}_{1\times 3}} \,\;8\times {{\boldsymbol 1}_{1\times 3}}\right]}^{\text{T}}}\times{{10}^{4}} $ 权重参数下限 $ {{\underline{\boldsymbol{W}}}_{k}}={{\left[ 1\times {{\boldsymbol 1}_{1\times 3}} \,\;2\times {{\boldsymbol 1}_{1\times 3}} \right]}^{\text{T}}}\times {{10}^{4}} $ 式(40)、(42)的
参数$ \begin{array}{c} {{\bar{p}}_{w}}=20,\; {{K}_{w1}}=50,\; {{K}_{w2}}=200,\;\\{{\gamma }_{w1}}=1,\; {{\gamma }_{w2}}=1\end{array} $
下载: 导出CSV
-
[1] Flores-Abad A, Ma O, Pham K, Ulrich S. A review of space robotics technologies for on-orbit servicing. Progress in Aerospace Sciences, 2014, 68: 1−26 doi: 10.1016/j.paerosci.2014.03.002 [2] Li W J, Cheng D Y, Liu X G, Wang Y B, Shi W H, Tang Z X, et al. On-orbit service (OOS) of spacecraft: A review of engineering developments. Progress in Aerospace Sciences, 2019, 108: 32−120 doi: 10.1016/j.paerosci.2019.01.004 [3] 黄攀峰, 鲁迎波, 张帆, 刘亚. 失效航天器接管控制技术发展综述. 上海航天(中英文), 2024, 41(3): 47−62Huang Pan-Feng, Lu Ying-Bo, Zhang Fan, Liu Ya. Overview of Takeover Control Technology for Failed Spacecraft. Aerospace Shanghai (Chinese & English), 2024, 41(3): 47−62 [4] Lin Z J, Wu B L, Wang D W. Specific tracking control of rotating target spacecraft under safe motion constraints. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(3): 2422−2438 doi: 10.1109/TAES.2022.3214799 [5] 袁利, 姜甜甜, 魏春岭, 杨孟飞. 空间控制技术发展与展望. 自动化学报, 2023, 49(3): 476−493Yuan Li, Jiang Tian-Tian, Wei Chun-Ling, Yang Meng-Fei. Advances and perspectives of space control technology. Acta Automatica Sinica, 2023, 49(3): 476−493 [6] Chang H T, Huang P F, Zhang Y Z, Meng Z J, Liu Z X. Distributed control allocation for spacecraft attitude takeover control via cellular space robot. Journal of Guidance, Control, and Dynamics, 2018, 41(11): 2499−2506 doi: 10.2514/1.G003626 [7] Lang X Y, de Ruiter A. A control allocation scheme for spacecraft attitude stabilization based on distributed average consensus. Aerospace Science and Technology, 2020, 106: Article No. 106173 doi: 10.1016/j.ast.2020.106173 [8] Han N, Luo J J, Zheng Z X, Sun J. Distributed cooperative game method for attitude takeover of failed satellites using nanosatellites. Aerospace Science and Technology, 2020, 106: Article No. 106151 doi: 10.1016/j.ast.2020.106151 [9] 吕跃勇, 方慧, 秦堂皓, 郭延宁. 组合体航天器输入-状态稳定姿态接管控制. 宇航学报, 2021, 42(7): 873−880Lyu Yue-Yong, Fang Hui, Qin Tang-Hao, Guo Yan-Ning. Input-to-state stable attitude takeover control for combined spacecraft. Journal of Astronautics, 2021, 42(7): 873−880 [10] Meng Z J, Li Q W. Optimal attitude takeover control for failed spacecraft based on multi-nanosatellites. Journal of the Franklin Institute, 2023, 360(7): 4947−4972 doi: 10.1016/j.jfranklin.2023.03.037 [11] Zhao Q, Duan G R. Exponential position and attitude tracking control of spacecraft with unbiased parameter identification. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(1): 1113−1128 doi: 10.1109/TAES.2023.3334252 [12] 常海涛, 黄攀峰, 鹿振宇, 孟中杰, 张夷斋. 空间细胞机器人接管非合作目标时的交互式参数辨识方法. 机器人, 2017, 39(2): 129−138Chang Hai-Tao, Huang Pan-Feng, Lu Zhen-Yu, Meng Zhong-Jie, Zhang Yi-Zhai. Interactive parameter identification of cellular space robots for non-cooperative spacecraft takeover control. Robot, 2017, 39(2): 129−138 [13] Han N, Luo J J, Ma W H, Yuan J P. Integrated identification and control for nanosatellites reclaiming failed satellite. Acta Astronautica, 2018, 146: 387−398 doi: 10.1016/j.actaastro.2018.03.006 [14] 张化光, 张欣, 罗艳红, 杨珺. 自适应动态规划综述. 自动化学报, 2013, 39(4): 303−311 doi: 10.1016/S1874-1029(13)60031-2Zhang Hua-Guang, Zhang Xin, Luo Yan-Hong, Yang Jun. An overview of research on adaptive dynamicprogramming. Acta Automatica Sinica, 2013, 39(4): 303−311 doi: 10.1016/S1874-1029(13)60031-2 [15] Dong H Y, Zhao X W, Hu Q L, Yang H Y, Qi P Y. Learning-based attitude tracking control with high-performance parameter estimation. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(3): 2218−2230 doi: 10.1109/TAES.2021.3130537 [16] Wei C S, Luo J J, Daio H H, Duan G R. Learning-based adaptive attitude control of spacecraft formation with guaranteed prescribed performance. IEEE Transactions on Cybernetics, 2019, 49(11): 4004−4016 doi: 10.1109/TCYB.2018.2857400 [17] 肖冰, 张海朝. 航天器姿态稳定强化学习鲁棒最优控制方法. 航空学报, 2024, 45(1): 628890Xiao Bing, Zhang Hai-Chao. Reinforcement learning robust optimal control for spacecraft attitude stabilization. Acta Aer-onautica et Astronautica Sinica, 2024, 45(1): 628890 [18] Ni Y, Yang H, Jiang B. Fault-tolerant coverage control of multiple satellites: A differential graphical game approach. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 5516−5529 [19] Liu Y H, Ma G F, Lyu Y Y, Wang P Y. Neural network-based reinforcement learning control for combined spacecraft attitude tracking maneuvers. Neurocomputing, 2022, 484: 67−78 doi: 10.1016/j.neucom.2021.07.099 [20] 韩楠, 罗建军, 马卫华. 失效卫星姿态接管的并行学习合作博弈控制. 航空学报, 2021, 42(3): 324307Han Nan, Luo Jian-Jun, Ma Wei-Hua. Concurrent learning cooperative game control for attitude takeover of failed satellites. Acta Aeronautica et Astronautica Sinica, 2021, 42(3): 324307 [21] Han N, Luo J J, Zong L J. Cooperative game method for on-orbit substructure transportation using modular robots. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(2): 1161−1175 doi: 10.1109/TAES.2021.3111141 [22] Wu H N, Wang M. Attitude takeover control of failed spacecraft via leader-followers adaptive cooperative game. Journal of Aerospace Information Systems, 2023, 20(11): 773−784 doi: 10.2514/1.I011242 [23] Chowdhary G. Concurrent Learning for Convergence in Adaptive Control Without Persistency of Excitation[Ph. D. dissertation]. Georgia Institute of Technology, USA, 2010. [24] 赵琴. 具有惯量参数辨识的组合体航天器位姿联合控制[博士论文]. 哈尔滨工业大学, 中国, 2022.Zhao Qin. Integrated Position and Attitude Control for Spacecraft With Inertia Parameter Identification[Ph. D. dissertation]. Harbin Institute of Technology, 2022. [25] Olfati-Sarber R, Fax J A, Murray R M. Consensus and cooperation in networked multi-agent systems. Proceedings of the IEEE, 2007, 95(1): 215−233 doi: 10.1109/JPROC.2006.887293 [26] Deptula P, Bell Z I, Doucette E A, Curtis J W, Dixon W E. Data-based reinforcement learning approximate optimal control for an uncertain nonlinear system with control effectiveness faults. Automatica, 2020, 116: Article No. 108922 doi: 10.1016/j.automatica.2020.108922 [27] Wang M L, Geng Y H, Wu B L, Wang D W. Distributed adaptive attitude takeover control of failed spacecraft with parameters identification. IEEE Transactions on Control Systems Technology, 2023, 31(2): 897−904 doi: 10.1109/TCST.2022.3187921 [28] Chowdhary G, Johnson E. A singular value maximizing data recording algorithm for concurrent learning. In: Proceedings of the 2011 American Control Conference. San Francisco, CA, USA: IEEE, 2011. 3547-3552 [29] Kamalapurkar R, Dinh H, Bhasin S, Dixon W E. Approximate optimal trajectory tracking for continuous-time nonlinear systems. Automatica, 2015, 51: 40−48 doi: 10.1016/j.automatica.2014.10.103 [30] Deptula P, Bell Z I, Zegres F M, Licitra R A, Dixon W E. Approximate optimal influence over an agent through an uncertain interaction dynamic. Automatica, 2021, 134: Article No. 109913 doi: 10.1016/j.automatica.2021.109913 -
下载:
计量
- 文章访问数: 35
- HTML全文浏览量: 22
- 被引次数: 0
