-
摘要: 针对具有输入时滞的非线性系统直接自适应最优控制问题, 提出一种新的数据驱动输出反馈控制方法. 该方法通过融合Q学习与值迭代和策略迭代, 在学习过程中无需依赖系统动力学知识. 在系统满足一致可观性的条件下, 提出一种基于输出数据和带有时滞的输入数据的系统状态重构方法, 基于值迭代和策略迭代来学习自适应最优控制策略. 最后, 将该方法应用于范德波尔振荡器这一经典非线性系统的控制, 并通过仿真结果充分验证了该方法的有效性.Abstract: This paper proposes a new data-driven output-feedback control method to address the direct adaptive optimal control problem for nonlinear systems with input time-delay. The combination of Q-learning with value iteration (VI) and policy iteration (PI) enables the learning process to be conducted without any knowledge of the system dynamics. Under the condition that the system is uniformly observable, we propose a novel method to reconstruct the state of the system based on output data and input data with time-delay. We then present two iterative methods, VI and PI, to learn the adaptive optimal control policy. Finally, the proposed methods are applied to the classical nonlinear system control——Van der Pol oscillator. The simulation results demonstrate the effectiveness of the proposed methods.
-
Key words:
- Optimal control /
- output-feedback /
- time-delay /
- adaptive dynamic programming
-
图 1 时滞系统的输出反馈控制器设计思路
Fig. 1 Design approach for output feedback controllers with time-delay system
图 3 考虑时滞的输出反馈下闭环系统的输入输出轨迹
Fig. 3 The input-output trajectories of the closed-loop system under output feedback with time-delay
图 4 不考虑时滞的输出反馈下闭环系统的输入输出轨迹
Fig. 4 The input-output trajectories of the closed-loop system under output feedback without time-delay
图 5 ${\mathrm{Q}}$函数迭代前后对比(除$u_k,\;u_{k-1}$外其他参数为0)
Fig. 5 Comparison of the ${\mathrm{Q}}$ function before and after iteration (with other parameters set to 0 except for $u_k$ and $u_{k-1}$)
图 8 ${\mathrm{Q}}$函数迭代前后对比(除$u_{k-2},\;u_{k-3}$外其他参数为0)
Fig. 8 Comparison of the ${\mathrm{Q}}$ function before and after iteration (with other parameters set to 0 except for $u_{k-2}$ and $u_{k-3}$)
图 6 ${\mathrm{Q}}$函数迭代前后对比(除$u_k,\;u_{k-3}$外其他参数为0)
Fig. 6 Comparison of the ${\mathrm{Q}}$ function before and after iteration (with other parameters set to 0 except for $u_k$ and $u_{k-3}$)
-
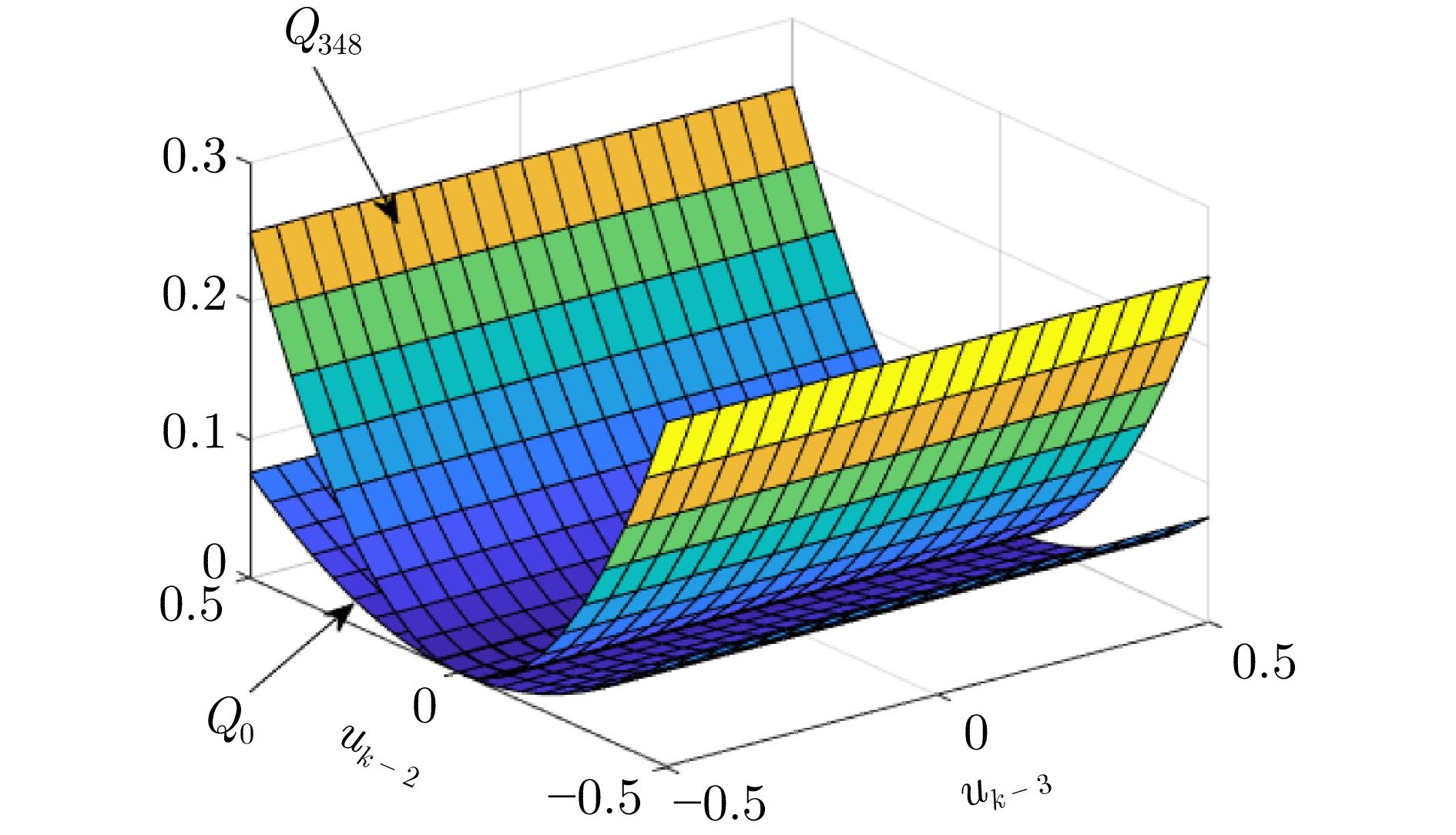
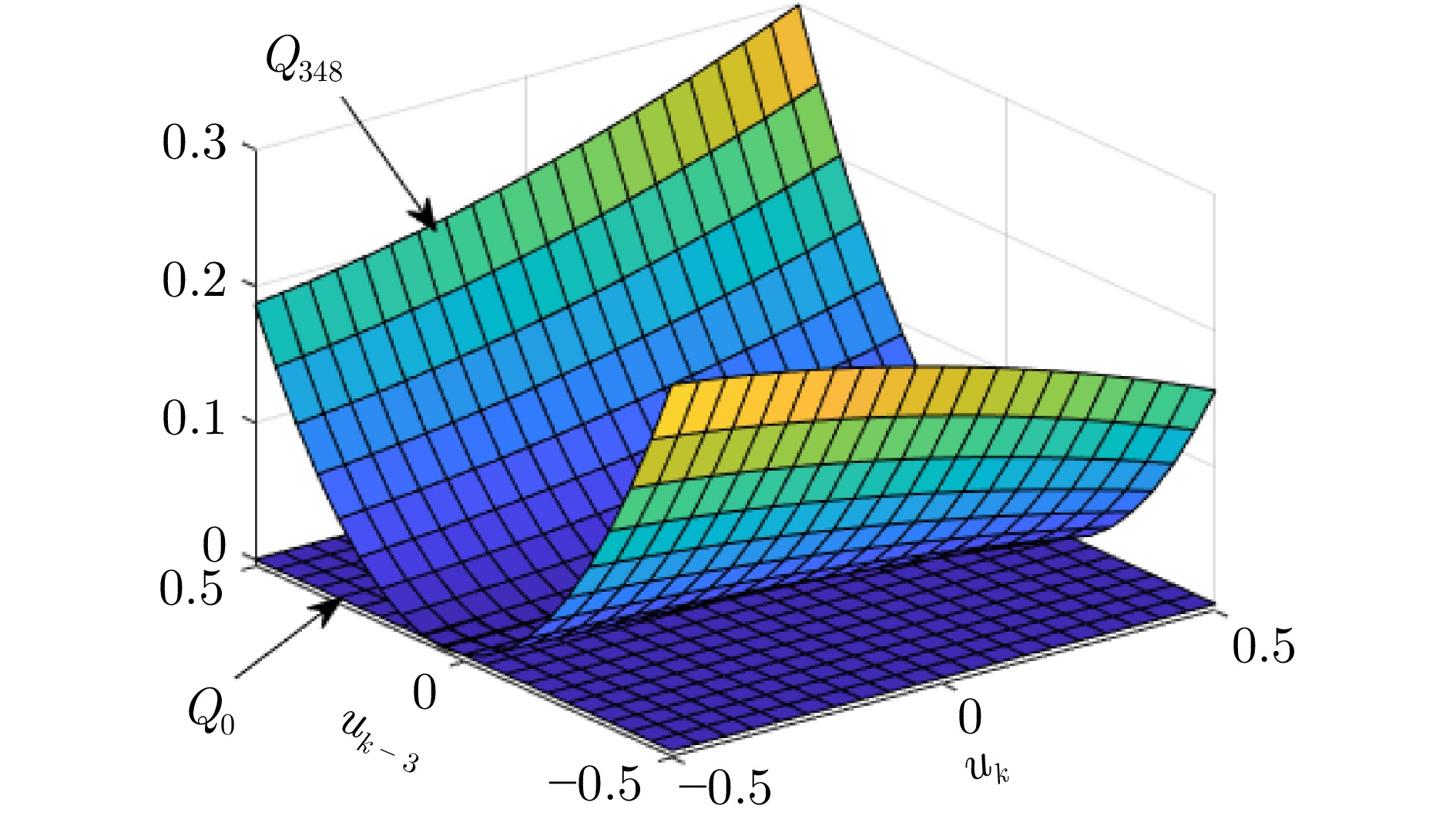
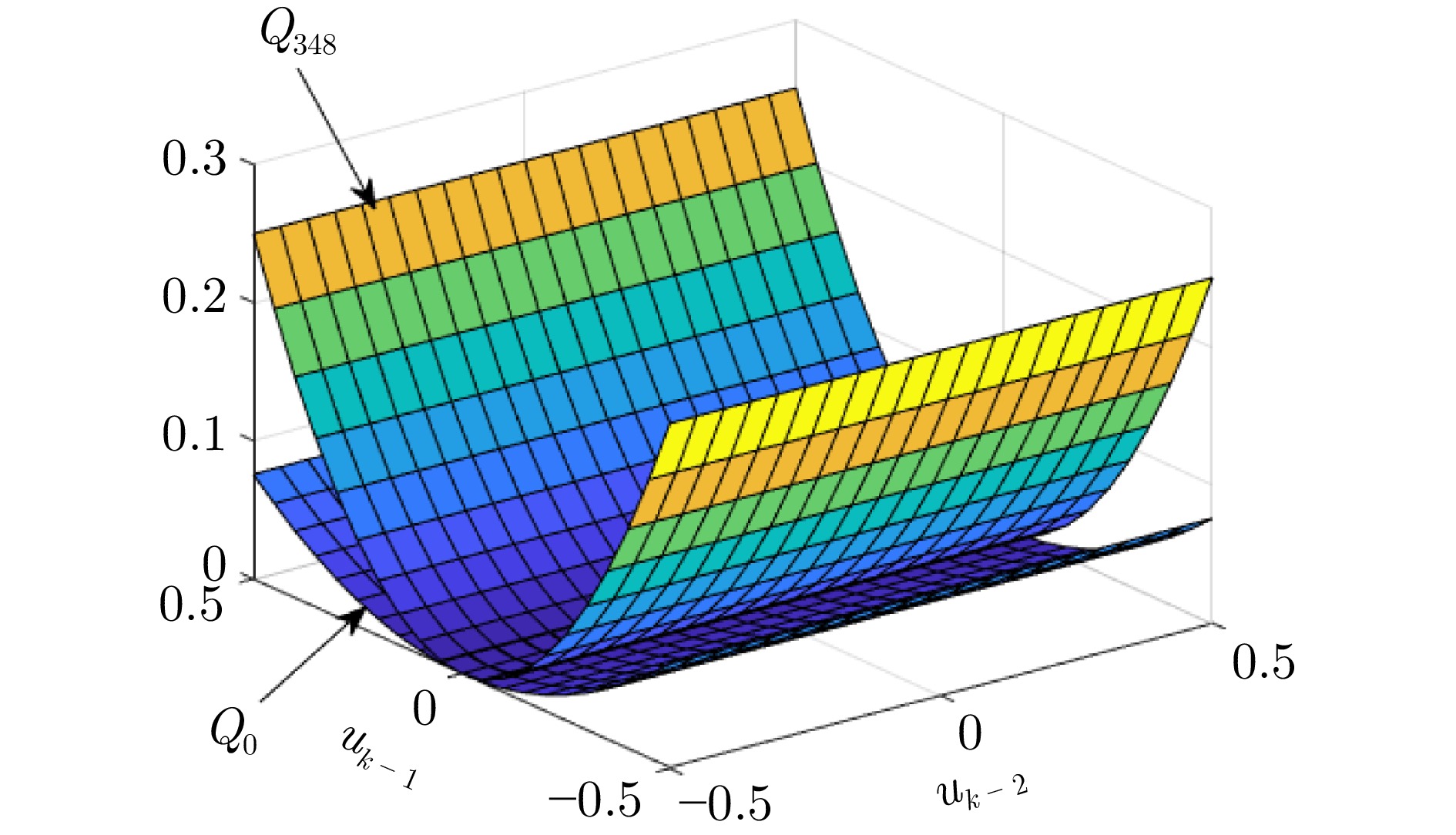
[1] Lewis F L, Vrabie D L, Syrmos V L. Optimal Control. Hoboken: Wiley, 2012. [2] Gao W N, Jiang Z P, Chai T Y. Bridging the gap between reinforcement learning and nonlinear output-feedback control. In: Proceedings of the 43rd Chinese Control Conference (CCC). Kunming, China: IEEE, 2024. 2425−2431 [3] Gao W N, Jiang Z P. Data-driven cooperative output regulation of multi-agent systems under distributed denial of service attacks. Science China Information Sciences, 2023, 66(9): Article No. 190201 doi: 10.1007/s11432-022-3702-4 [4] Hou Z S, Wang Z. From model-based control to data-driven control: Survey, classification and perspective. Information Sciences, 2013, 235: 3−35 doi: 10.1016/j.ins.2012.07.014 [5] Bu X H, Yu Q X, Hou Z S, Qian W. Model free adaptive iterative learning consensus tracking control for a class of nonlinear multiagent systems. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 49(4): 677−686 doi: 10.1109/TSMC.2017.2734799 [6] Hou Z S, Xiong S S. On model-free adaptive control and its stability analysis. IEEE Transactions on Automatic Control, 2019, 64(11): 4555−4569 doi: 10.1109/TAC.2019.2894586 [7] Liu S D, Lin G, Ji H H, Jin S T, Hou Z S. A novel enhanced data-driven model-free adaptive control scheme for path tracking of autonomous vehicles. IEEE Transactions on Intelligent Transportation Systems, 2025, 26(1): 579−590 doi: 10.1109/TITS.2024.3487299 [8] Xiong S S, Hou Z S. Model-free adaptive control for unknown MIMO nonaffine nonlinear discrete-time systems with experimental validation. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(4): 1727−1739 doi: 10.1109/TNNLS.2020.3043711 [9] 董昱辰, 高伟男, 姜钟平. 基于分布式自适应内模的多智能体系统协同最优输出调节. 自动化学报, 2025, 51(3): 678−691Dong Yu-Chen, Gao Wei-Nan, Jiang Zhong-Ping. Cooperative optimal output regulation for multi-agent systems based on distributed adaptive internal model. Acta Automatica Sinica, 2025, 51(3): 678−691 [10] Lewis F L, Liu D R. Reinforcement Learning and Approximate Dynamic Programming for Feedback Control. Hoboken: Wiley, 2013. [11] Vrabie D, Vamvoudakis K G, Lewis F L. Optimal Adaptive Control and Differential Games by Reinforcement Learning Principles. London: Institution of Engineering and Technology, 2013. [12] Jiang Y, Jiang Z P. Global adaptive dynamic programming for continuous-time nonlinear systems. IEEE Transactions on Automatic Control, 2015, 60(11): 2917−2929 doi: 10.1109/TAC.2015.2414811 [13] Wei Q L, Liu D R, Liu Y, Song R Z. Optimal constrained self-learning battery sequential management in microgrid via adaptive dynamic programming. IEEE/CAA Journal of Automatica Sinica, 2017, 4(2): 168−176 doi: 10.1109/JAS.2016.7510262 [14] Zhang H G, Liu D R, Luo Y H, Wang D. Adaptive Dynamic Programming for Control: Algorithms and Stability. London: Springer, 2013. [15] Lewis F L, Vrabie D, Vamvoudakis K G. Reinforcement learning and feedback control: Using natural decision methods to design optimal adaptive controllers. IEEE Control Systems Magazine, 2012, 32(6): 76−105 doi: 10.1109/MCS.2012.2214134 [16] Liu D R, Wei Q L, Wang D, Yang X, Li H L. Adaptive Dynamic Programming With Applications in Optimal Control. Cham: Springer, 2017. [17] Yang Y L, Modares H, Vamvoudakis K G, He W, Xu C Z, Wunsch D C. Hamiltonian-driven adaptive dynamic programming with approximation errors. IEEE Transactions on Cybernetics, 2022, 52(12): 13762−13773 doi: 10.1109/TCYB.2021.3108034 [18] Gao W N, Jiang Z P. Learning-based adaptive optimal output regulation of linear and nonlinear systems: An overview. Control Theory and Technology, 2022, 20(1): 1−19 doi: 10.1007/s11768-022-00081-3 [19] Liu D R, Wei Q L. Policy iteration adaptive dynamic programming algorithm for discrete-time nonlinear systems. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(3): 621−634 doi: 10.1109/TNNLS.2013.2281663 [20] Li C, Liu D R, Wang D. Data-based optimal control for weakly coupled nonlinear systems using policy iteration. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(4): 511−521 doi: 10.1109/TSMC.2016.2606479 [21] Zhao B, Wang D, Shi G, Liu D R, Li Y C. Decentralized control for large-scale nonlinear systems with unknown mismatched interconnections via policy iteration. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(10): 1725−1735 doi: 10.1109/TSMC.2017.2690665 [22] Gao W N, Jiang Z P, Chai T Y. Resilient control under denial-of-service and uncertainty: An adaptive dynamic programming approach. IEEE Transactions on Automatic Control, 2025, 70(6): 4085−4092 doi: 10.1109/TAC.2025.3527305 [23] Jiang Y, Jiang Z P. Computational adaptive optimal control for continuous-time linear systems with completely unknown dynamics. Automatica, 2012, 48(10): 2699−2704 doi: 10.1016/j.automatica.2012.06.096 [24] Kleinman D. On an iterative technique for Riccati equation computations. IEEE Transactions on Automatic Control, 1968, 13(1): 114−115 doi: 10.1109/TAC.1968.1098829 [25] Wei Q L, Liu D R, Lin H Q. Value iteration adaptive dynamic programming for optimal control of discrete-time nonlinear systems. IEEE Transactions on Cybernetics, 2016, 46(3): 840−853 doi: 10.1109/TCYB.2015.2492242 [26] Gao W N, Mynuddin M, Wunsch D C, Jiang Z P. Reinforcement learning-based cooperative optimal output regulation via distributed adaptive internal model. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(10): 5229−5240 doi: 10.1109/TNNLS.2021.3069728 [27] Gao W N, Huang M Z, Jiang Z P, Chai T Y. Sampled-data-based adaptive optimal output-feedback control of a 2-degree-of-freedom helicopter. IET Control Theory and Applications, 2016, 10(12): 1440−1447 [28] Liu D R, Wei Q L. Adaptive dynamic programming for a class of discrete-time non-affine nonlinear systems with time-delays. In: Proceedings of the International Joint Conference on Neural Networks (IJCNN). Barcelona, Spain: IEEE, 2010. 1−6 [29] Xiao F, Shi Y, Ren W. Robustness analysis of asynchronous sampled-data multiagent networks with time-varying delays. IEEE Transactions on Automatic Control, 2018, 63(7): 2145−2152 doi: 10.1109/TAC.2017.2756860 [30] Liu Y, Zhang H G, Yu R, Xing Z X. H∞ tracking control of discrete-time system with delays via data-based adaptive dynamic programming. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2020, 50(11): 4078−4085 doi: 10.1109/TSMC.2019.2946397 [31] Gao W N, Jiang Z P. Adaptive optimal output regulation of time-delay systems via measurement feedback. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(3): 938−945 doi: 10.1109/TNNLS.2018.2850520 [32] Gao W N, Jiang Y, Jiang Z P, Chai T Y. Output-feedback adaptive optimal control of interconnected systems based on robust adaptive dynamic programming. Automatica, 2016, 72: 37−45 doi: 10.1016/j.automatica.2016.05.008 [33] Lewis F L, Vamvoudakis K G. Reinforcement learning for partially observable dynamic processes: Adaptive dynamic programming using measured output data. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2011, 41(1): 14−25 doi: 10.1109/TSMCB.2010.2043839 [34] Moraal P E, Grizzle J W. Observer design for nonlinear systems with discrete-time measurements. IEEE Transactions on Automatic Control, 1995, 40(3): 395−404 doi: 10.1109/9.376051 [35] Heydari A. Analyzing policy iteration in optimal control. In: Proceedings of the American Control Conference (ACC). Boston, USA: IEEE, 2016. 5728−5733 -
下载:
图(8)
计量
- 文章访问数: 155
- HTML全文浏览量: 60
- PDF下载量: 63
- 被引次数: 0
