-
摘要: 由于容易实施, 基于投影梯度的分布式在线优化模型逐渐成为一种主流的在线学习方法. 然而, 在处理大数据应用时, 投影步骤成为该方法的计算瓶颈. 近年来, 研究者提出了面向凸代价函数的分布式在线条件梯度算法, 其悔界为${\rm O}(T^{3/4})$, 其中$T$是一个时间范围. 该算法存在两方面的问题, 一是其悔界劣于公认的悔界${\rm O}(\sqrt{T})$; 二是没有分析非凸代价函数的收敛性能, 而实际应用中代价函数大部分是非凸函数. 因此, 提出一种基于条件梯度的加速分布式在线学习算法, 使用Frank-Wolfe 步骤替代投影步骤, 避免昂贵的投影计算. 文中证明当局部代价函数为凸函数时, 所提算法达到公认的悔界${\rm O}(\sqrt{T})$; 当局部代价函数为潜在非凸函数时, 所提算法以速率${\rm O}(\sqrt{T})$收敛到平稳点. 最后, 仿真实验验证了所提算法的性能与理论证明的结论.Abstract: The distributed online optimization model based on projected gradient has become a prominent paradigm for online learning due to its simplicity. However, this paradigm is incapable of handling massive data applications because the projection step becomes the computational bottleneck. Recent studies have presented the distributed online conditional gradient algorithms for convex cost functions, which achieved an O(T 3/4) regret bound, where T is a time horizon. There are two negative problems for those algorithms. The first one is that the regret bound of those algorithms is worse than the well known regret bound ${\rm O}(\sqrt{T})$. The second one is that the convergence performance of the presented algorithms has not been analyzed for non-convex cost functions, which are common in practice. In this paper, we propose an accelerated distributed online learning algorithm based on the conditional gradient method over networks, which avoids the prohibitively expensive projection steps by using Frank-Wolfe step. Moreover, when the local cost functions are convex, we show that the regret bound of ${\rm O}(\sqrt{T})$ is achieved. When the local cost functions are potentially non-convex, we also show that the algorithm converges to some stationary points at rate of ${\rm O}(\sqrt{T})$. Finally, the performance of the proposed algorithm and the theoretical results are verified by simulation experiments.
-
Key words:
- Conditional gradient /
- distributed online learning /
- regret bound /
- convergence rate
-
图 1 在news20和aloi数据集上不同节点数下本文算法的性能
Fig. 1 Performance of the proposed algorithm at different nodes on news20 and aloi datasets
图 2 在news20和aloi数据集上64节点下本文算法和D-OCG算法的性能比较
Fig. 2 The performance comparison between the proposed algorithm and the D-OCG algorithm at 64 nodes on news20 and aloi datasets
图 3 本文算法在具有固定64个节点和不同拓扑结构的news20和aloi数据集上的性能
Fig. 3 Performance of the proposed algorithm on news20 and aloi datasets with fixed 64 nodes and different topologies
-
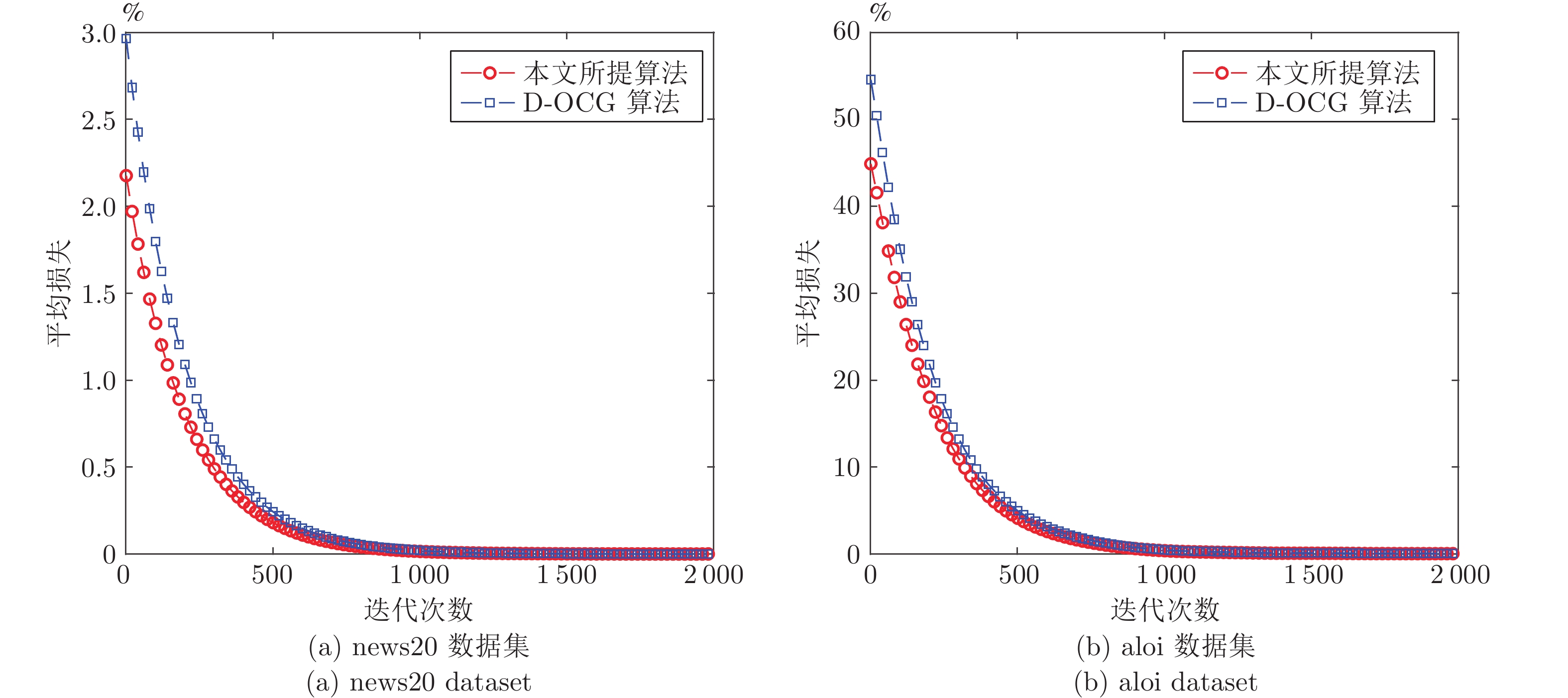
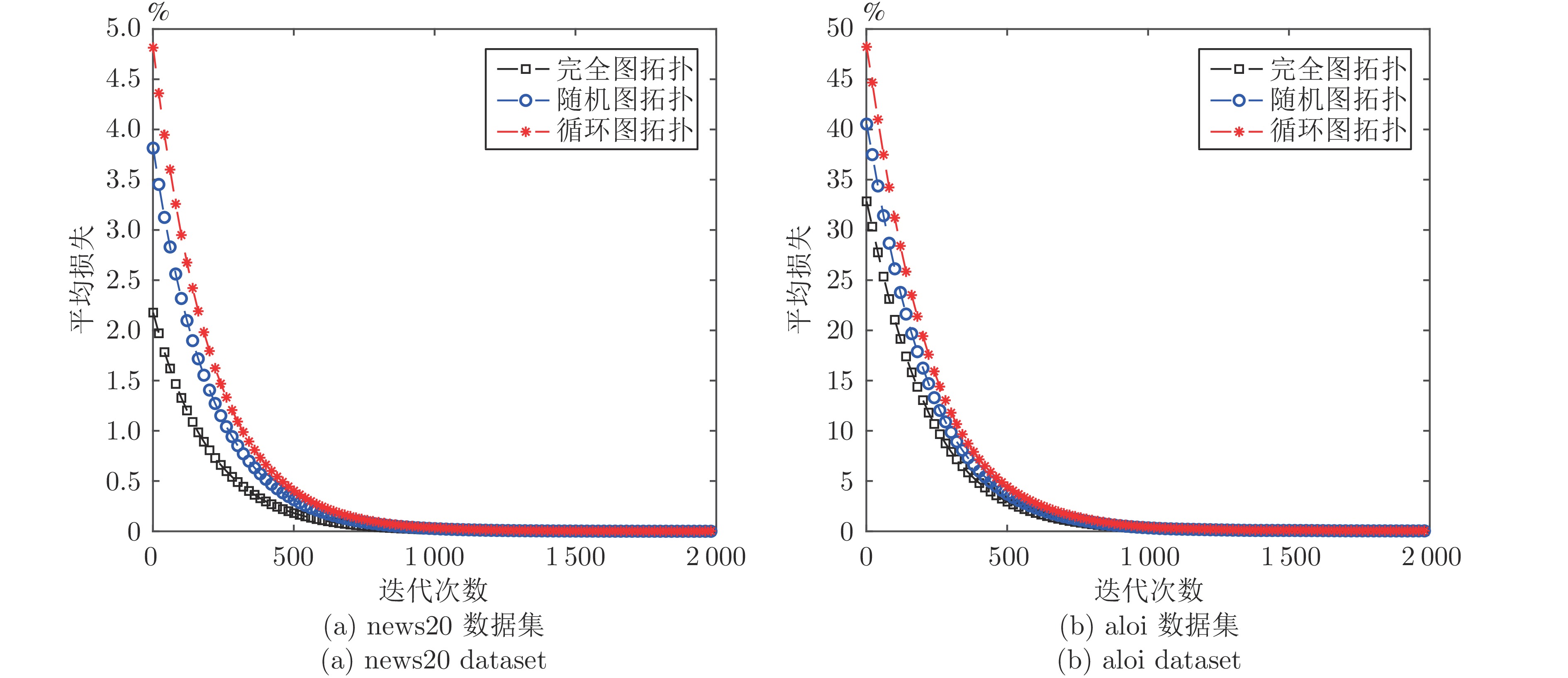
[1] Zhu J L, Xu C Q, Guan J F, Wu D P. Differentially private distributed online algorithms over time-varying directed networks. IEEE Transactions on Signal and Information Processing over Networks, 2018, 4(1): 4−17 [2] Rabbat M, Nowak R. Distributed optimization in sensor networks. In: Proceedings of the 3rd International Symposium on Information Processing in Sensor NetworksProc. Berkeley, USA: IEEE, 2004. 20−27 [3] Zhang M C, Hao B W, Ge Q B, Zhu J L, Zheng R J, Wu Q T. Distributed adaptive subgradient algorithms for online learning over time-varying networks. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(7): 4518−4529 [4] Abu-Elkheir M, Hayajneh M, Abu A N. Data management for the internet of things: design primitives and solution. Sensors, 2013, 13(11): 15582-15612 doi: 10.3390/s131115582 [5] 孙路明, 张少敏, 姬涛, 李翠平, 陈红. 人工智能赋能的数据管理技术研究. 软件学报, 2020, 31(3): 600-619SUN Lu-Ming, ZHANG Shao-Min, JI Tao, LI Cui-Ping, CHEN Hong. Survey of data management techniques powered by artificial intelligence. Journal of Software, 2020, 31(3): 600-619 [6] 黄刚, 李军华. 基于 AC-DSDE 进化算法多 UAVs协同目标分配. 自动化学报, 2021, 47(1): 173-184Huang Gang, Li Jun-Hua. Multi-UAV cooperative target allocation based on AC-DSDE evolutionary algorithm. Acta Automatica Sinica, 2021, 47(1): 173-184 [7] Beck A, Nedić A, Ozdaglar A, Teboulle M. An ${\rm{ O}}(1/k)$ gradient method for network resource allocation problems. IEEE Transactions on Control of Network Systems, 2014, 1(1): 64-73 doi: 10.1109/TCNS.2014.2309751 [8] 刘妹琴, 韩学艳, 张森林, 郑荣濠, 兰剑. 基于水下传感器网络的目标跟踪技术研究现状与展望. 自动化学报, 2021, 47(2): 235-251Liu Mei-Qin, Han Xue-Yan, Zhang Sen-Lin, Zheng Rong-Hao, Lan Jian. Research status and prospect of target tracking technologies via underwater sensor networks. Acta Automatica Sinica, 2021, 47(2): 235-251 [9] 蒋弘毅, 王永娟, 康锦煜. 目标检测模型及其优化方法综述. 自动化学报, 2021, 47(6): 1232-1255Jiang Hong-Yi, Wang Yong-Juan, Kang Jin-Yu. A survey of object detection models and its optimization methods. Acta Automatica Sinica, 2021, 47(6): 1232-1255 [10] Wen G H, Yu X H, Liu Z W, Yu W W. Adaptive consensus-based robust strategy for economic dispatch of smart grids subject to communication uncertainties. IEEE Transactions on Industrial Informatics, 2018, 14(6): 2484-2496 doi: 10.1109/TII.2017.2772088 [11] 李小玲, 王怀民, 郭长国, 丁博, 李小勇. 分布式约束优化问题研究及其进展. 计算机学报, 2015, 38(8): 1656-1671 doi: 10.11897/SP.J.1016.2015.01656LI Xiao-Ling, WANG Huai-Min, GUO Chang-Guo, DING Bo, LI Xiao-Yong. Research and development of distributed constraint optimization problems. Chinese Journal of Computers, 2015, 38(8): 1656-1671 doi: 10.11897/SP.J.1016.2015.01656 [12] Nedić A, Olshevsky A. Distributed optimization over time-varying directed graphs. IEEE Transactions on Automatic Control, 2015, 60(3): 601-615 doi: 10.1109/TAC.2014.2364096 [13] Qu G N, Li N. Harnessing smoothness to accelerate distributed optimization. IEEE Transactions on Control of Network Systems, 2018, 5(3): 1245-1260 doi: 10.1109/TCNS.2017.2698261 [14] Shalev-Shwartz S. Online learning and online convex optimization. Foundations and Trends R in Machine Learning, 2011, 4(2): 107-194 doi: 10.1561/2200000018 [15] Hazan E, Kalai A, Kale S, Agarwal A. Logarithmic regret algorithms for online convex optimization. In: Proceedings of the International Conference on Computational Learning Theory. Berlin, Germany: Springer, 2006. 499−513 [16] Mateos-Núñez D, Cortés J. Distributed online convex optimization over jointly connected digraphs. IEEE Transactions on Network Science and Engineering, 2014, 1(1): 23-37 doi: 10.1109/TNSE.2014.2363554 [17] Xu C Q, Zhu J L, Wu D O. Decentralized online learning methods based on weight-balancing over time-varying digraphs. IEEE Transactions on Emerging Topics in Computational Intelligence, 2021, 5(3): 394-406 doi: 10.1109/TETCI.2018.2880771 [18] Akbari M, Gharesifard B, Linder T. Distributed online convex optimization on time-varying directed graphs. IEEE Transactions on Control of Network Systems, 2017, 4(3): 417-428 doi: 10.1109/TCNS.2015.2505149 [19] Raginsky M, Kiarashi N, Willett R. Decentralized online convex programming with local information. In: Proceedings of the American Control Conference. San Francisco, USA: IEEE, 2011. 5363−5369 [20] Hosseini S, Chapman A, Mesbahi M. Online distributed convex optimization on dynamic networks. IEEE Transactions on Automatic Control, 2016, 61(11): 3545-3550 doi: 10.1109/TAC.2016.2525928 [21] Yan F, Sundaram S, Vishwanathan S V N, Qi Y. Distributed autonomous online learning: regrets and intrinsic privacy-preserving properties. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(11): 2483-2493 doi: 10.1109/TKDE.2012.191 [22] Liu S, Xie L H, Quevedo D E. Event-Triggered quantized communication-based distributed convex optimization. IEEE Transactions on Control of Network Systems, 2018, 5(1): 167-178 doi: 10.1109/TCNS.2016.2585305 [23] Liang Q K, Modiano E. Network utility maximization in adversarial environments. In: Proceedings of the IEEE Conference on Computer Communications. Honolulu, USA: IEEE, 2018. 594−602 [24] Frank M, Wolfe P. An algorithm for quadratic programming. Naval Research Logistics Quarterly, 1956, 3(1-2): 95-110 doi: 10.1002/nav.3800030109 [25] Jaggi M. Revisiting Frank-Wolfe: Projection-free sparse convex optimization. In: Proceedings of the 30th International Conference Machine Learning. Atlanta, USA: JMLR, 2013. 427−435 [26] Clarkson K L. Coresets, sparse greedy approximation, and the Frank-Wolfe algorithm. ACM Transactions on Algorithms, 2010, 6(4): 1-34 [27] Zhu J L, Wu Q T, Zhang M C, Zheng R J, Li K Q. Projection-free decentalized online learning for submodular maximization over time-varying networks. Journal of Machine Learning Research, 2021, 22: 1-42 [28] Hazan E, Kale S. Projection-free online learning. In: Proceedings of the 29th International Conference Machine Learning. Edinburgh, UK: JMLR, 2012. 521−528 [29] Garber D, Hazan E. A linearly convergent variant of the conditional gradient algorithm under strong convexity, with applications to online and stochastic optimization. SIAM Journal on Optimization, 2016, 26(3): 1493-1528 doi: 10.1137/140985366 [30] Lafond J, Wai H T, Moulines E. On the online Frank-Wolfe algorithms for convex and non-convex optimizations. arXiv preprint arXiv: 1510.01171, 2016. [31] Hazan E, Luo H P. Variance-reduced and projection-free stochastic optimization. In: Proceedings of the 33rd International Conference on International Conference on Machine Learning. New York, USA: JMLR, 2016. 1263−1271 [32] Wai H T, Lafond J, Scaglione A, Moulines E. Decentralized Frank-Wolfe algorithm for convex and non-convex problems. IEEE Transactions on Automatic Control, 2017, 62(11): 5522-5537 doi: 10.1109/TAC.2017.2685559 [33] Zhang W P, Zhao P L, Zhu W W, Hoi S, Zhang T. Projection-free distributed online learning in networks. In: Proceedings of the 34th Intentional Conference of Machine Learning. Sydney, Australia: PMLR, 2017. 4054−4062 [34] Wan Y Y, Tu W W, Zhang L J. Projection-free distributed online convex optimization with ${{\rm{ O}}(\sqrt{T})}$ communication complexity. In: Proceedings of the 37th International Conference on Machine Learning. Virtual Event: PMLR, 2020. 9818−9828 [35] Boyd S, Vandenberghe L. Convex Optimization. Cambridge: Cambridge University, 2004. [36] Liu S, Qiu Z R, Xie L H. Convergence rate analysis of distributed optimization with projected subgradient algorithm. Automatica, 2017, 83: 162-169 doi: 10.1016/j.automatica.2017.06.011 [37] Watts D J, Strogatz S H. Collective dynamics of 'small-world' networks. Nature, 1998, 393: 440-442 doi: 10.1038/30918 -
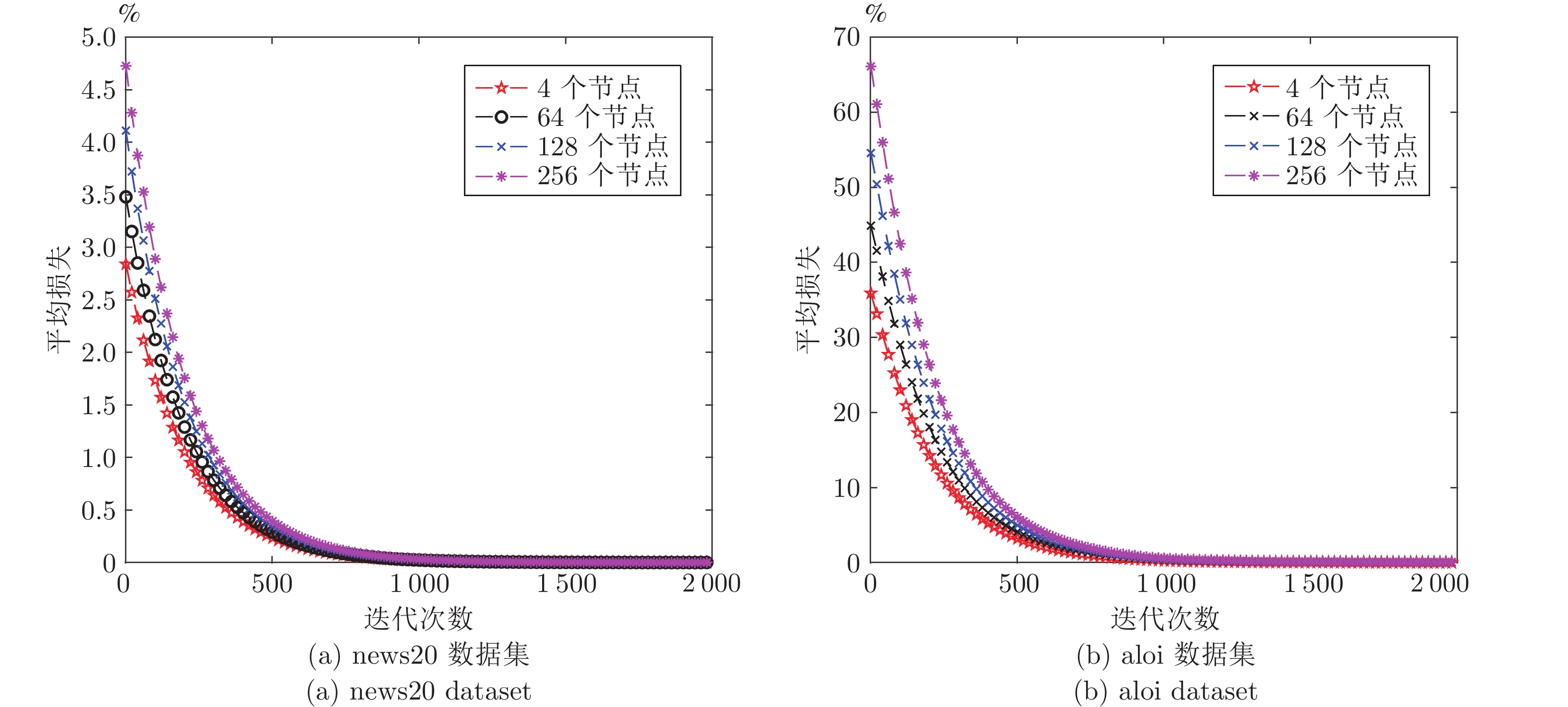
下载:
图(3) / 表(1)
计量
- 文章访问数: 803
- HTML全文浏览量: 178
- PDF下载量: 188
- 被引次数: 0
