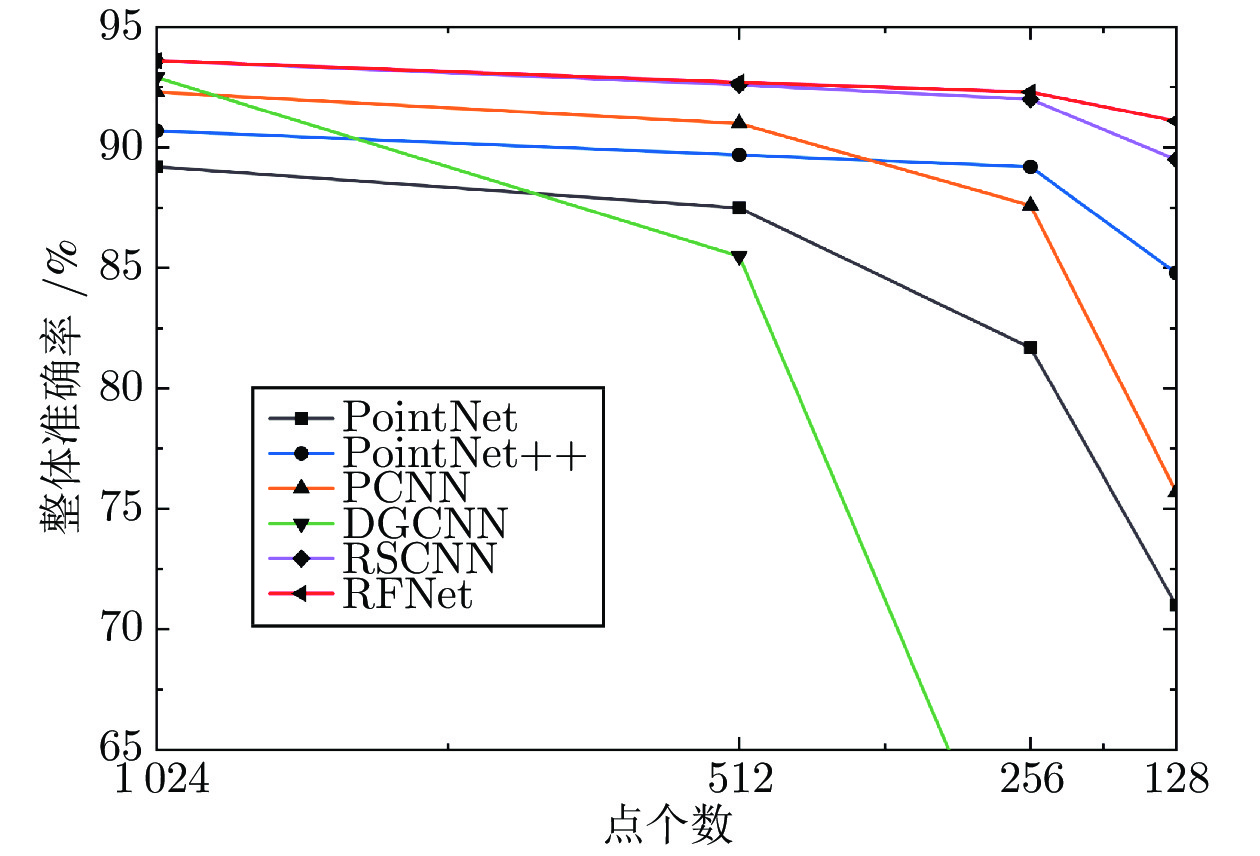
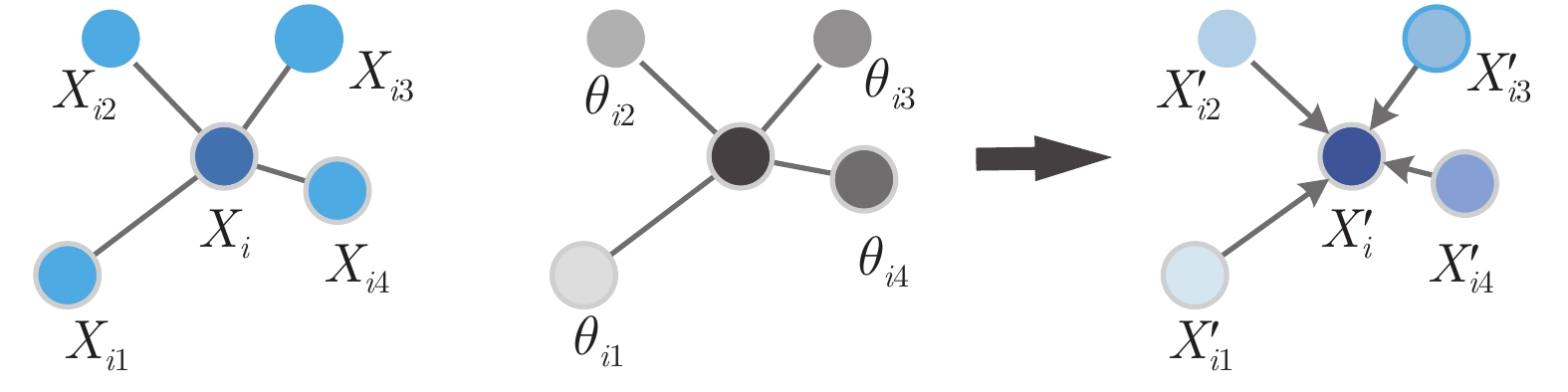
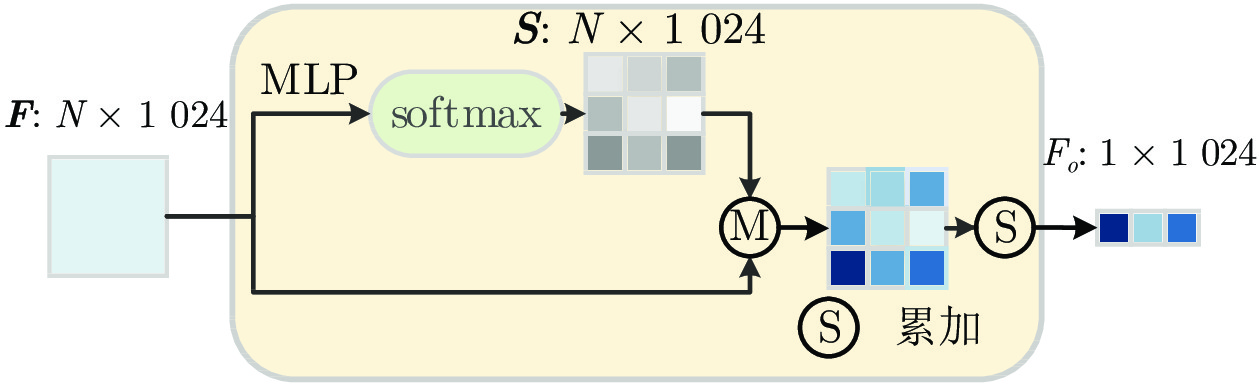
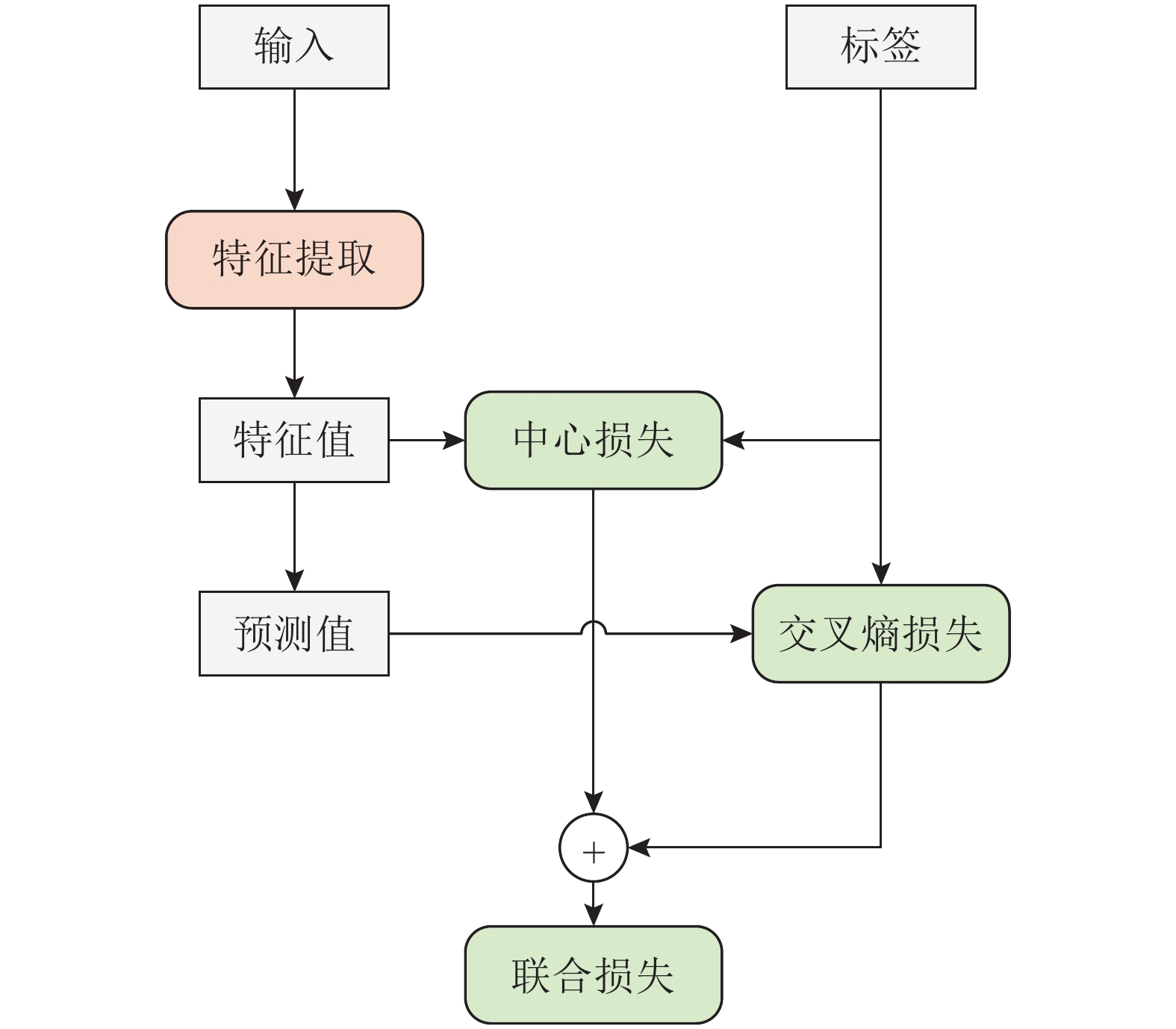
-
摘要: 由于点云的非结构性和无序性, 目前已有的点云分类网络在精度上仍然需要进一步提高. 通过考虑局部结构的构建、全局特征聚合和损失函数改进三个方面, 构造一个有效的点云分类网络. 首先, 针对点云的非结构性, 通过学习中心点特征与近邻点特征之间的关系, 为不规则的近邻点分配不同的权重, 以此构建局部结构; 然后, 使用注意力思想, 提出加权平均池化(Weighted average pooling, WAP), 通过自注意力方式, 学习每个高维特征的注意力分数, 在应对点云无序性的同时, 可以有效地聚合冗余的高维特征; 最后, 利用交叉熵损失与中心损失之间的互补关系, 提出联合损失函数(Joint loss function, JL), 在增大类间距离的同时, 减小类内距离, 进一步提高了网络的分类能力. 在合成数据集ModelNet40、ShapeNetCore和真实世界数据集ScanObjectNN上进行实验, 与目前性能最好的多个网络相比较, 验证了该整体网络结构的优越性.Abstract: Due to the unstructured and disordered nature of point cloud, the classification accuracy is still needed to improve for the currently existed point cloud classification approaches. In this paper, an effective point cloud classification network is proposed by considering local structure construction, global feature aggregation, and loss function improvement. Firstly, in view of the unstructured nature of point cloud, the local structure is constructed via assigning different weights to those irregular neighborhood points, which are computed via the relationship between the center point feature and its neighbor feature. Moreover, a strategy of weighted average pooling (WAP) is designed to learn the attention score of each high-dimensional feature through self-attention mechanization, which can effectively aggregate redundant high-dimensional features while coping with point cloud disorder. In addition, a joint loss function (JL) is presented by utilizing the complementary relationship between the cross-entropy loss and the center loss, which increases the inter-class distance while reduces the intro-class distance, and further improves the classification ability of the network. Compared to several state-of-the-art networks, the experimental results on the synthetic dataset ModelNet40 and ShapeNetCore and the real-world dataset ScanObjectNN demonstrate the superiority of the overall network structure.
-
Key words:
- Deep learning /
- 3D point cloud /
- point cloud classification /
- attention mechanism /
- loss function
-
图的同构判定在有机化学、计算机科学和人工智能(机器学习或模式识别中常使用图的邻接矩阵特征值来判定两个对象是否为同一个对象)等领域有着重要的应用[1−3]. 上世纪前半叶, 与图同构相关的问题主要围绕图的邻接矩阵特征值及其应用展开[4], 取得若干重要的理论成果和一批应用成果; 其中一个重要的发现是, 两个互不同构的无向图却具有相同的邻接矩阵特征多项式, 即用邻接矩阵特征多项式判定两个无向图是否同构有时会得出错误的结果[4].
上世纪70年代, Karp和Johnson认为图的同构判定问题是少数几个既不能归类为 P 问题也不能归类为 NP 的问题[1, 3]. 此后, 该问题成为理论计算机领域的公开问题并受到广泛重视. 1982年, Luks给出一个当时最好的两图同构判定算法, 其时间复杂度是$\exp ({\text{O(}}\sqrt {n\log n} {\text{)}}$)[5−6] ($ n $为图的顶点数). 此后40多年来, 几百篇这方面的文章得以在不同的学术期刊上发表[1]. 2015年, Babai[6]在Luks算法的基础上, 给出两图同构判定问题的拟多项式算法, 其时间复杂度是$ \exp ({(\log n)^{{\text{O(1)}}}}) $. Babai的工作虽然是一个重要进展, 但图的同构判定问题是否在多项式时间内可解仍然悬而未决[1, 3].
图的同构判定问题的另一研究路径是设计可执行的判定算法, 大致可以分为传统和非传统两类判定算法. 传统判定算法有两类: 1) 针对一些特殊图[7−8] (如树和极大外平面图)的同构判定算法(如Ullman算法和Schmidt算法等[9]). 2) 针对一般简单图的同构判定算法, 如一些放在因特网上用于测试两图是否同构的程序(如Nauty和Saucy等[3, 6]). 非传统判定算法也有两类: 1) 基于遗传算法和神经网络的智能判定算法. 这些算法将图的同构判定问题转化为一类优化求解问题, 但其判定结果并不完全可靠. 2) 基于DNA计算[9]和量子计算的判定算法. 这类算法虽然高效, 但不能回答图的同构判定是 P 问题还是 NP 问题. 无向连通图的距离矩阵是素矩阵(邻接矩阵一般不是素矩阵), 它具有邻接矩阵所没有的独特性质[10]. 文献[10]揭示了简单无向图同构与距离矩阵同构之间的一般关系, 将基于邻接矩阵的同构判定条件推广到距离矩阵, 给出几个适合一般简单无向图的同构判定条件. 这些条件均是充要条件且均具有多项式时间复杂度. 上述成果是近年来图同构研究方面的一个重要进展.
简单无向图的同构关系可由其距离矩阵的同构关系确定, 但复杂无向图却不能. 其根本原因在于: 复杂无向图中的自环和顶点间的重边对顶点间的距离没有影响[10]; 换言之, 自环数或重边数不同的复杂无向图可能具有完全相同的距离矩阵. 因文献[10]所给的判定条件不能用于复杂无向图, 故寻找和发现复杂无向图的同构判定条件既是必须的也是重要的. 本文的主要贡献是: 1) 针对一般复杂无向图的同构判定问题, 给出了基于邻接矩阵之和的特征多项式判定条件. 2) 针对复杂无向连通图的同构判定问题, 给出了基于距离矩阵特征多项式和邻接矩阵特征多项式的同构判定条件. 将该条件用于复杂无向不连通图的各个连通子图, 就可解决复杂无向不连通图的同构判定问题. 上述两个判定条件均是充要条件且均具有多项式时间复杂度. 此外, 当复杂无向图退化为简单无向图时, 上述两个判定条件仍然适用.
1. 相关概念和预备知识
定义1[4, 11−12]. 图$ G $是一个二元组, 记作$ G = \langle V, E \rangle $, 其中:
1) $ V = \{ {v_1},\;{v_2},\; \cdots ,\;{v_n}\left| {\left| V \right| = n,\;{\text{ 1}} \le n < \infty } \right.\} $, $ {v_i} \in V $称为$ G $的顶点, $ V $称为$ G $的顶点集.
2) $ E = \{ {e_1},\;{e_2},\; \cdots ,\;{e_m}\left| {\left| E \right| = m,\;{\text{ 0}} \le m < \infty } \right.\} $, $ {e_j} \in E $称为$ G $的边, $ E $称为$ G $的边集.
3) $ \forall {e_j} \in E $: $ {e_j} $为无向边时, 称$ G $为无向图, $ {e_j} $为有向边时, 称$ G $为有向图.
4) 连接同一顶点的边称为自环, 两顶点间的多条无向边或多条方向相同的有向边称为重边. 既无自环也无重边的图称为简单图, 否则称为复杂图.
在现有文献报道的复杂无向图中, 每个顶点最多有一个自环. 若无特别声明, 本文讨论的均是顶点最多有一个自环的复杂无向图.
定义2[11−13]. 设$ G = \left\langle {V,\;E} \right\rangle $是无向图, $ V = \{ {v_1}, {v_2},\; \cdots ,\;{v_n}\} $. 若$ {v_i} $和$ {v_j} $之间有$ k $ ($ k = 0,\;1,\; \cdots $)条边, 令$ {a_{ij}} = k $; 称由元素$ {a_{ij}} $构成的矩阵$ A({a_{ij}}) \in {{\bf{R}}^{n \times n}} $为无向图$ G $的邻接矩阵.
定义2既适合简单无向图也适合复杂无向图($ {a_{ij}} \in \{ 0,\;1,\;2,\; \cdots \} $). 无向图的邻接矩阵是非负整数对称矩阵.
定义3[14]. 设$ {I_n} \in {{\bf{R}}^{n \times n}} $为单位矩阵, 交换$ {I_n} $的第$ i $行和第$ j $行(或第$ i $列与第$ j $列)所得的矩阵$ P(i,\;j) $称为对换矩阵, 对换矩阵的乘积称为置换矩阵.
引理1[14]. 对换矩阵和置换矩阵具有如下性质:
1) 置换矩阵的乘积仍是置换矩阵;
2) 设$ Q $是置换矩阵, 则$ \det (Q) = \pm 1 $;
3) 设$ Q $是置换矩阵, 则$ {Q^{\text{T}}} $和$ {Q^{ - 1}} $也是置换矩阵, 且$ {Q^{\text{T}}} = {Q^{ - 1}} $;
4) 置换矩阵是正交矩阵;
5) 置换矩阵是幂幺矩阵, 即若$ Q $是置换矩阵, 则$ {Q^m} = {I_n} $, $ m $是某自然数.
由定义3和引理1可知, 对换矩阵和$ {I_n} $也是置换矩阵.
定义4[10]. 设$ A,\;B \in {{\bf{R}}^{n \times n}} $, $ \Omega \subset {{\bf{R}}^{n \times n}} $为全体$ n $阶置换矩阵的集合. 若存在置换矩阵$ Q \in \Omega $, 使得$ A = {Q^{\text{T}}}BQ $, 则称$ A $与$ B $同构, 记作$ A \cong B $; 此外, 称$ {Q^{\text{T}}}BQ $是对$ B $的同构变换.
图的同构问题可以这样表述: 给定两个图, 当忽略图中顶点标号、顶点间相对位置、边的长短和曲直信息时, 问这两个图是否具有相同的结构?
定义5[4, 12−13]. 设$ {G_{\text{1}}} = \left\langle {{V_{\text{1}}},\;{E_{\text{1}}}} \right\rangle $和$ {G_2} = $ $ \langle {V_2}, {E_{\text{2}}} \rangle $是两个图. 若存在一个从$ {V_1} $到$ {V_2} $的一一映射$ g $: $ \forall {v_i},\;{v_j} \in {V_1} $, $ {v_i} $至$ {v_j} $有$ k $条边, 当且仅当$ g({v_i}), g({v_j}) \in {V_2} $, 且$ g({v_i}) $至$ g({v_j}) $也有$ k $条边, 则称$ {G_1} $和$ {G_2} $同构, 记作$ {G_1} \cong {G_2} $.
定义5既适合简单图也适合复杂图($ k \in \{ 0, 1,\;2,\; \cdots \} $).
引理2[10−11]. 设$ {G_{\text{1}}} = \left\langle {{V_{\text{1}}},\;{E_{\text{1}}}} \right\rangle $和$ {G_2} = $$ \left\langle {{V_{\text{2}}},\;{E_{\text{2}}}} \right\rangle $是两个图, $ \left| {{V_1}} \right| = \left| {{V_2}} \right| = n $, $ A $与$ B $分别是$ {G_1} $和$ {G_2} $的邻接矩阵, 则$ {G_1} \cong {G_2} $的充要条件是存在$ n $阶置换矩阵$ Q \in \Omega $, 使得$ A = {Q^{\text{T}}}BQ $.
引理2适合一切无向和有向图. 由定义4和引理2可知, 两图同构与该两图的邻接矩阵同构等价.
定义6[4, 10−13]. 设$ G = \left\langle {V,\;E} \right\rangle $是无向图, $ V = \{ {v_1},\;{v_2},\; \cdots ,\;{v_n}\} $, $ E = \{ {e_1},\;{e_2},\; \cdots ,\;{e_m}\} $: 1) $ G $中顶点与边的交替序列$ W = {v_1}{e_1}{v_2}{e_2} \cdots {v_k}{e_k}{v_{k + 1}} $ ($ k \le n - 1 $)称为$ G $的链, 各边互异的链称为迹, 各顶点互异的链称为路, 当$ W $是路时, $ W $中的边数$ k $称为$ W $的长度, 记作$ k = \left| W \right| $; 2) 设$ {v_i} $和$ {v_j} $是$ V $中任意两个顶点, 当$ {v_i} $和$ {v_j} $之间有$ s $条路$ {W_s}{\text{ }} $时, 称$ d({v_i},\;{v_j}) = $$ \min \{ {k_p} = \left| {{W_p}} \right|\left| {1 \le p \le s} \right.\} $为$ {v_i} $和$ {v_j} $之间的距离; 若$ {v_i} $和$ {v_j} $之间无路($ G $不连通), 约定$ d({v_i},\;{v_j}) = \infty $.
定义7[10, 13]. 设$ G = \left\langle {V,\;E} \right\rangle $是无向图, $ V = \{ {v_1}, {v_2},\; \cdots ,\;{v_n}\} $, $ {d_{ij}} = d({v_i},\;{v_j}) $表示顶点$ {v_i} $和$ {v_j} $($ 1 \le i, j \le n $)之间的距离: 当$ i = j $时, 令$ {d_{ii}} = 0 $; 当$ i \ne j $且$ d({v_i},\;{v_j}) = k $ ($ d({v_i},\;{v_j}) = \infty $)时, 令$ {d_{ij}} = k $$ ({d_{ij}} = \infty ) $, 其中$ k \ge 1 $为正整数, 称由元素$ {d_{ij}} $构成的矩阵$ D({d_{ij}}) \in {{\bf{R}}^{n \times n}} $为无向图$ G $的距离矩阵.
由定义6和定义7可知: 1) 复杂无向图中的自环和顶点间的重边对顶点间的距离没有影响; 2) 当$ G $是无向连通图时, 距离矩阵$ D $是对角线元素均为零而其他元素均为正整数的对称矩阵.
定义8[12−13]. 设$ {G_n} = \left\langle {V,\;E} \right\rangle $是简单无向图, $ V = \{ {v_1},\;{v_2},\; \cdots ,\;{v_n}\} $, $ n \ge 2 $, 若$ \forall i \ne j $, $ {v_i} $和$ {v_j} $之间恰有一条边, 则称$ {G_n} $为无向完全图, 其邻接矩阵记为$ {A_n} $.
由定义2和定义8可知, $ {A_n} $的对角线元素均为0而其他元素均为1. 设$ {G_n} $的距离矩阵为$ {D_n} $, 由定义7可知, $ {D_n} = {A_n} $, 即$ {A_n} $既是$ {G_n} $的邻接矩阵又是$ {G_n} $的距离矩阵.
定义9. 设$ { T} \subset {{\bf{R}}^{n \times n}} $$ (n \ge 2) $表示全体$ n $阶正交矩阵的集合; $ {\Omega ^ - } = \{ - S\left| {S \in \Omega } \right.\} $表示全体$ n $阶负置换矩阵的集合; $ \Phi = \Omega \cup {\Omega ^ - } $表示全体$ n $阶置换矩阵和全体$ n $阶负置换矩阵的并集; $ \Theta = { T} - \Phi $表示$ { T} $中除$ \Phi $之外全体$ n $阶正交矩阵的集合.
由定义9和正交矩阵的性质可知: $ \Theta \cap \Phi = \emptyset $($ \emptyset $为空集), $ \Theta \cup \Phi = { T} $; $ \forall {Q_1},\;{Q_2} \in \Phi $, $ {Q_1}{Q_2} \in \Phi $; $ \forall Q \in \Phi $, $ \forall P \in \Theta $, $ QP,\;{\text{ }}PQ \in \Theta $; $ \forall P \in \Theta $, $ \forall E \in \Phi $, $ \forall Q \in { T} $且$ Q \ne E{P^{\text{T}}} $, $ QP,\;{\text{ }}PQ \in \Theta $.
2. 复杂无向图的同构判定方法
为简便计, $ \forall A \in {{\bf{R}}^{n \times n}} $$ (n \ge 2) $, 本文用$ {f_\lambda }(A) $表示$ A $的特征多项式 $ \det (\lambda {I_n} - A) $, 即$ {f_\lambda }(A) = \det (\lambda {I_n} - A) $.
推论1. 设$ {G_{\text{1}}} = \left\langle {{V_{\text{1}}},\;{E_{\text{1}}}} \right\rangle $和$ {G_{\text{2}}} = \left\langle {{V_{\text{2}}},\;{E_{\text{2}}}} \right\rangle $是两个无向图, $ \left| {{V_1}} \right| = \left| {{V_2}} \right| = n $, $ A $与$ B $分别是$ {G_1} $和$ {G_2} $的邻接矩阵, 若$ {f_\lambda }(A) \ne {f_\lambda }(B) $, 则$ {G_1} $和$ {G_2} $不同构.
证明. 设$ {f_\lambda }(A) \ne {f_\lambda }(B) $时, $ {G_1} \cong {G_2} $. 由引理2可知, 当$ {G_1} \cong {G_2} $时, 存在$ n $阶置换矩阵$ Q \in \Omega $, 使得$ A = {Q^{\text{T}}}BQ $. 由此, $ {f_\lambda }(A) = $ $ {f_\lambda }({Q^{\text{T}}}BQ) = {f_\lambda }(B) $, 与假设相矛盾. 故$ {f_\lambda }(A) \ne {f_\lambda }(B) $时, $ {G_1} $和$ {G_2} $不同构.
□ 推论1既适合简单无向图也适合复杂无向图. 需要强调的是, 即使$ {f_\lambda }(A) = {f_\lambda }(B) $, 也不能保证$ {G_1} $和$ {G_2} $同构. 邻接矩阵特征多项式相等仅是两个无向图同构的必要条件[10, 15].
设$ A({a_{ij}}) \in {{\bf{R}}^{n \times n}} $$ (n \ge 2) $是对称矩阵: 若$ {a_{ij}} $全是正整数, 则称$ A $为正整数对称矩阵; 若$ {a_{ij}} $为零或正整数, 则称$ A $为非负整数对称矩阵.
引理3[10]. 设$ A \in {{\bf{R}}^{n \times n}} $$ (n \ge 2) $是对角线元素均为1而其他元素均为正整数的对称矩阵, 则$ \forall P \in \Theta $, $ {P^{\text{T}}}AP $不是正整数对称矩阵.
引理4[14]. 设$ A \in {{\bf{R}}^{n \times n}} $, 则$ A $为正交矩阵的充要条件是存在正交矩阵$ P \in { T} $, 使得
$$ {P^{\text{T}}}AP = {P^{ - 1}}AP = \left[ {\begin{array}{*{20}{c}} {{I_s}}&{}&{} \\ {}&{ - {I_t}}&{} \\ {}&{}&{{H_\theta }} \end{array}} \right] = {P_\theta } $$ 其中, $ {I_s} $与$ I_{t} $分别是$ s $阶和$ t $阶单位矩阵,
$$ {H_\theta } = \left[ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\cos {\theta _1}}&{\sin {\theta _1}} \\ { - \sin {\theta _1}}&{\cos {\theta _1}} \end{array}} \right]}&{}&{} \\ {}& \ddots &{} \\ {}&{}&{\left[ {\begin{array}{*{20}{c}} {\cos {\theta _k}}&{\sin {\theta _k}} \\ { - \sin {\theta _k}}&{\cos {\theta _k}} \end{array}} \right]} \end{array}} \right] $$ $ s + t + 2k = n $, $ {\theta _j} \in {\bf{R}} $$ (1 \le j \le k) $为实数.
由正交矩阵的定义可知, $ {P_\theta } $和$ {H_\theta } $均是正交矩阵.
定理1. 设$ A \in {{\bf{R}}^{n \times n}} $$ (n \ge 2) $是对角线元素为0或1而其他元素均为正整数的对称矩阵, 则$ \forall P \in \Theta $, $ {P^{\text{T}}}AP $既不是正整数对称矩阵也不是非负整数对称矩阵.
证明. 当$ A $的对角线元素全为1时, 由引理3可知, $ \forall P \in \Theta $, $ {P^{\text{T}}}AP $不是正整数对称矩阵. 当$ A $的对角线元素全为0时, 设$ B = A + {I_n} $. 由引理3可知, $ \forall P \in \Theta $, $ {P^{\text{T}}}BP $不是正整数对称矩阵. 因$ {P^{\text{T}}}BP = {P^{\text{T}}}AP + {I_n} $, 故$ \forall P \in \Theta $, $ {P^{\text{T}}}AP $不是非负整数对称矩阵. 当$ A $的对角线元素不全为0也不全为1时, 以下用归纳法证明: $ \forall P \in \Theta $, $ {P^{\text{T}}}AP $不是非负整数对称矩阵.
当$ n = 2 $时, 设
$$ A = \left[ {\begin{array}{*{20}{c}} {{\delta _1}}&a \\ a&{{\delta _2}} \end{array}} \right] ,\; P = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta } \\ { - \sin \theta }&{\cos \theta } \end{array}} \right] $$ 其中, $ {\delta _1},\;{\delta _2} \in \{ 0,\;1\} $, $ {\delta _1} + {\delta _2} = 1 $, $ a \ge 1 $为正整数, $ \theta \in {\bf{R}} $. 设$ {\vartheta _1} = \sin 2\theta $, $ {\vartheta _2} = \cos 2\theta $, $ C = {P^{\text{T}}}AP $, 可得
$$ C = \left[ {\begin{array}{*{20}{c}} {{{\sin }^2}\theta + {\delta _1}{\vartheta _2} - a{\vartheta _1}}&{({\delta _1} - 0.5){\vartheta _1} + a{\vartheta _2}} \\ {({\delta _1} - 0.5){\vartheta _1} + a{\vartheta _2}}&{{{\cos }^2}\theta - {\delta _1}{\vartheta _2} + a{\vartheta _1}} \end{array}} \right] $$ 当$ \theta \ne \pm k\pi $$ (k = 0,\;1,\;2,\; \cdots ) $时, $ P \in \Theta $, $ C $不是非负整数对称矩阵($ C $的元素中有负数或小数). 当$ P \in \Theta $时, 由定义9和引理4可知, 对一切2阶正交矩阵$ E \in \Phi $, $ Z \in {\rm T} $且$ Z \ne E{P^{ - 1}} $, 则: 1) $ {J_1} = ZP \in \Theta $, $ {J_2} = PZ \in \Theta $, $ {J_3} = {Z^{\text{T}}}PZ \in \Theta $; 2) $ J_1^{\text{T}}A{J_1} $, $ J_2^{\text{T}}A{J_2} $, $ J_3^{\text{T}}A{J_3} $均不是非负整数对称矩阵. 由此, 对一切2阶正交矩阵$ J \in \Theta $, $ {J^{\text{T}}}AJ $不是非负整数对称矩阵.
当$ n = 3 $时, 设
$$ A = \left[ {\begin{array}{*{20}{c}} {{\delta _1}}&{{a_1}}&{{a_2}} \\ {{a_1}}&{{\delta _2}}&{{a_3}} \\ {{a_2}}&{{a_3}}&{{\delta _3}} \end{array}} \right] ,\; P = \left[ {\begin{array}{*{20}{c}} \delta &0&0 \\ 0&{\cos \theta }&{\sin \theta } \\ 0&{ - \sin \theta }&{\cos \theta } \end{array}} \right] $$ 其中, $ {\delta _1},\;{\delta _2},\;{\delta _3} \in \{ 0,\;1\} $, $ 1 \le {\delta _1} + {\delta _2} + {\delta _3} \le 2 $, $ {a_i} \ge 1 $ $ (1 \le i \le 3) $为正整数, $ \delta = \pm 1 $, $ \theta \in {\bf{R}} $. 设$ {\vartheta _1} = \sin 2\theta $, $ {\vartheta _2} = \cos 2\theta $, $ \alpha (\theta ) = {a_1}\cos \theta - {a_2}\sin \theta $, $ \beta (\theta ) = {a_1}\sin \theta $ $ +{a_2}\cos \theta $, $ \eta = {\delta _2} - {\delta _3} $, $ \mu (\theta ) = \eta {\sin ^2}\theta $, $ C = {P^{\mathrm{T}}}AP $, 可得
$$ C = \left[ {\begin{array}{*{20}{c}} {{\delta _1}}&{\delta \alpha (\theta )}&{\delta \beta (\theta )} \\ {\delta \alpha (\theta )}&{{\delta _2} - \mu (\theta ) - {a_3}{\vartheta _1}}&{0.5\eta {\vartheta _1} + {a_3}{\vartheta _2}} \\ {\delta \beta (\theta )}&{0.5\eta {\vartheta _1} + {a_3}{\vartheta _2}}&{{\delta _3} + \mu (\theta ) + {a_3}{\vartheta _1}} \end{array}} \right] $$ 当$ \delta = 1 $且 $ \theta \ne \pm 2l\pi $$ (l = 0,\;1,\;2,\; \cdots ) $, 或者$ \delta = - 1 $且$ \theta \ne \pm h\pi $ ($ h $为奇数)时, $ P \in \Theta $, $ C $不是非负整数对称矩阵. 类似$ n = 2 $时的分析可得, 对一切3阶正交矩阵$ J \in \Theta $, $ {J^{\text{T}}}AJ $不是非负整数对称矩阵.
当$ n \ge 4 $时, 设
$$ A = \left[ {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}&{{A_{13}}} \\ {A_{12}^{\text{T}}}&{{A_{22}}}&{{A_{23}}} \\ {A_{13}^{\text{T}}}&{A_{23}^{\text{T}}}&{{A_{33}}} \end{array}} \right] ,\; {P_\theta } = \left[ {\begin{array}{*{20}{c}} {{I_s}}&{}&{} \\ {}&{ - {I_t}}&{} \\ {}&{}&{{H_\theta }} \end{array}} \right] $$ 其中, $ {A_{11}} \in {{\bf{R}}^{s \times s}} $、$ {A_{22}} \in {{\bf{R}}^{t \times t}} $和$ {A_{33}} \in {{\bf{R}}^{2k \times 2k}} $均是对角线元素为0或1而其他元素全是正整数的分块对称矩阵; $ {A_{12}} $, $ {A_{13}} $, $ {A_{23}} $均是分块正整数矩阵; $ A $的对角线元素之和满足$ 1 \le \sum\nolimits_i {{a_{ii}}} \le n - 1 $; $ {H_\theta } $为形如引理4中的矩阵, $ s + t + 2k = n $, $ {\theta _j} \in {\bf{R}} $$ (1 \le j \le k) $为实数. 由此,
$$ P_\theta ^{\text{T}}A{P_\theta } = \left[ {\begin{array}{*{20}{c}} {{A_{11}}}&{ - {A_{12}}}&{{A_{13}}{H_\theta }} \\ { - A_{12}^{\text{T}}}&{{A_{22}}}&{ - {A_{23}}{H_\theta }} \\ {H_\theta ^{\text{T}}A_{13}^{\text{T}}}&{ - H_\theta ^{\text{T}}A_{23}^{\text{T}}}&{H_\theta ^{\text{T}}{A_{33}}{H_\theta }} \end{array}} \right] $$ 1) 当$ s = n $, 或$ 1 \le s < n $, $ t = 0 $且所有的$ {\theta _j} = \pm 2l\pi $$ (l = 0,\;1,\;2,\; \cdots ) $, 或$ s = t = 0 $且所有的$ {\theta _j} = \pm 2l\pi $$ (l = 0,\;1,\;2,\; \cdots ) $时, $ {P_\theta } = {I_n} \in \Omega $.
2) 当$ t = n $, 或$ 1 \le t < n $, $ s = 0 $且所有的$ {\theta _j} = \pm h\pi $($ h $为奇数), 或$ t = s = 0 $且所有的$ {\theta _j} = \pm h\pi $($ h $为奇数)时, $ {P_\theta } = - {I_n} \in \Phi $.
3) 当$ s,\;t,\;k $和$ {\theta _j} $$ (1 \le j \le k) $的取值不是上述两种情况时, $ {P_\theta } \in \Theta $, $ P_\theta ^{\text{T}}A{P_\theta } $不是非负整数对称矩阵.
当$ P \in \Theta $时, 由定义9和引理4可知, 对一切$ n \ge 4 $阶正交矩阵$ E \in \Phi $, $ Z \in {T} $且$ Z \ne E{P^{ - 1}} $, 则: a) $ {J_1} = ZP \in \Theta $, $ {J_2} = PZ \in \Theta $, $ {J_3} = {Z^{\text{T}}}PZ \in \Theta $; b) $ J_1^{\text{T}}A{J_1} $, $ J_2^{\text{T}}A{J_2} $, $ J_3^{\text{T}}A{J_3} $均不是非负整数对称矩阵. 由此, 对一切$ n \ge 4 $阶正交矩阵$ J \in \Theta $, $ {J^{\text{T}}}AJ $不是非负整数对称矩阵.
综上可得, $ \forall n \ge 2 $, $ \forall P \in \Theta $, $ {P^{\text{T}}}AP $不是非负整数对称矩阵.
□ 此外, 不难证明, $ \forall n \ge 2 $, $ \forall Q \in \Phi $, $ {Q^{\text{T}}}AQ $是非负整数对称矩阵.
使用定义8中的符号$ {A_n} $和引理2, 可以得到如下推论.
推论2. 设$ {G_{\text{1}}} = \left\langle {{V_{\text{1}}},\;{E_{\text{1}}}} \right\rangle $和$ {G_2} = \left\langle {{V_{\text{2}}},\;{E_{\text{2}}}} \right\rangle $是两个无向图, $ \left| {{V_1}} \right| = \left| {{V_2}} \right| = n \ge 2 $, $ A $与$ B $分别是$ {G_1} $和$ {G_2} $的邻接矩阵, 则$ {G_1} \cong {G_2} $的充要条件是存在$ n $阶置换矩阵$ Q \in \Omega $, 使得$ A + {A_n} = {Q^{\text{T}}}(B + {A_n})Q $.
证明. 设$ A + {A_n} = {Q^{\text{T}}}(B + {A_n})Q $. 由定义3和引理1可知, 置换矩阵$ Q \in \Omega $$ (Q \ne {I_n}) $可表示为$ m $ ($ m \ge 2 $为正整数)个对换矩阵$ P({i_s},\;{j_s}) = {P_s} $的乘积, 即$ Q = P({i_1},\;{j_1}) \cdots P({i_m},\;{j_m}) = {P_1} \cdots {P_m}$. 此外, 不难验证, 任给对换矩阵$ {P_s} $, $ P_s^{\text{T}}{A_n}{P_s} = {A_n} $. 由此可得: $ {Q^{\text{T}}}{A_n}Q = P_m^{\text{T}} \cdots P_1^{\text{T}}{A_n}{P_1} \cdots {P_m} = {A_n} $; $ A\; + {A_n} = $$ {Q^{\text{T}}}(B + {A_n})Q = {Q^{\text{T}}}BQ + {A_n} $; $ A = {Q^{\text{T}}}BQ $. 再由引理2可得, $ {G_1} \cong {G_2} $.
设$ {G_1} \cong {G_2} $. 由引理2可知, 存在$ n $阶置换矩阵$ Q \in \Omega $, 使得$ A = {Q^{\text{T}}}BQ $. 由上述充分性证明可知, $ \forall Q \in \Omega $, $ {A_n} = {Q^{\text{T}}}{A_n}Q $. 由此, $ A + {A_n} = {Q^{\text{T}}}(B + {A_n})Q $.
□ 容易理解, 推论2适合一切无向图.
引理5[14]. 设$ C,\;B \in {{\bf{R}}^{n \times n}} $是对称矩阵, 则$ {f_\lambda }(C) = {f_\lambda }(B) $的充要条件是存在$ n $阶正交矩阵$ P \in {T} $, 使得$ C = {P^{\text{T}}}BP $.
基于前面的分析和准备, 下面给出两个无向图的同构判定条件.
定理2. 设$ {G_{\text{1}}} = \left\langle {{V_{\text{1}}},\;{E_{\text{1}}}} \right\rangle $和$ {G_2} = \left\langle {{V_{\text{2}}},\;{E_{\text{2}}}} \right\rangle $是两个无向图, 每个顶点最多有一个自环, $ \left| {{V_1}} \right| = \left| {{V_2}} \right| = n \ge 2 $, $ {A_1} $与$ {A_2} $分别是$ {G_1} $和$ {G_2} $的邻接矩阵, 则$ {G_1} \cong {G_2} $的充要条件是$ {f_\lambda }({A_1} + {A_n}) = {f_\lambda }({A_2} + {A_n}) $.
证明. 设$ {f_\lambda }({A_1} + {A_n}) = {f_\lambda }({A_2} + {A_n}) $. 给$ {G_1} $和$ {G_2} $中的每两个顶点之间加一条边, 可以得到两个新的无向图$ {\hat G_1} $和$ {\hat G_2} $, 其邻接矩阵分别是$ {A_1} + {A_n} $和$ {A_2} + {A_n} $. 因$ {G_1} $和$ {G_2} $的顶点最多有一个自环, 由定义2可知, $ {A_1} $和$ {A_2} $的对角线元素为0或1 (可以全为0, 也可全为1); 再由定义8可知, $ {A_1} + {A_n} $和$ {A_2} + {A_n} $均是对角线元素为0或1而其他元素均是正整数的对称矩阵, 即$ {A_1} + {A_n} $和$ {A_2} + {A_n} $均是非负整数对称矩阵. 由引理5可知, 当$ {f_\lambda }({A_1} + {A_n}) = {f_\lambda }({A_2} + {A_n}) $时, 存在正交矩阵$ Q \in { T} $, 使得$ {A_1} \;+ {A_n} = {Q^{\text{T}}}({A_2} + {A_n})Q $. 由定理1可知, $ Q \notin \Theta $; 否则, $ {A_1} + {A_n} $将不是非负整数矩阵. 因$ Q \in { T} = \Phi \cup \Theta $且$ Q \notin \Theta $, 故$ Q \in \Phi $. 由此, 存在$ Q \in \Omega $ (或$ - Q \in \Omega $), 使得$ {A_1} + {A_n} = {Q^{\text{T}}}({A_2} + {A_n})Q $; 再由推论2可知, $ {G_1} \cong {G_2} $.
设$ {G_1} \cong {G_2} $. 因$ {G_1} \cong {G_2} $, 故存在$ n $阶置换矩阵$ Q \in \Omega $, 使得$ {A_1} = {Q^{\text{T}}}{A_2}Q $. 由推论2的证明结果可知, $ {A_n} = {Q^{\text{T}}}{A_n}Q $. 由此, $ {A_1} + {A_n} = $$ {Q^{\text{T}}}({A_2} + {A_n})Q $, $ {f_\lambda }({A_1} + {A_n}) = {f_\lambda }({A_2} + {A_n}) $.
□ 需要说明的是: 1) 定理2既适合复杂无向图也适合简单无向图, 既适合连通无向图也适合不连通无向图; 一言以蔽之, 定理2适合一切无向图. 2) 因求解特征多项式$ {f_\lambda }(A) $的算法复杂度是$ {\mathrm{O}}({n^3}) $[16−17], 故使用定理2判定两个无向图是否同构的算法复杂度是$ 2{\mathrm{O}}({n^3}) $.
引理6[10]. 设$ {G_{\text{1}}} = \left\langle {{V_{\text{1}}},\;{E_{\text{1}}}} \right\rangle $和$ {G_{\text{2}}} = \left\langle {{V_{\text{2}}},\;{E_{\text{2}}}} \right\rangle $是两个简单无向连通图, $ \left| {{V_1}} \right| = \left| {{V_2}} \right| = n \ge {\text{2}} $, $ {D_1} $与$ {D_2} $分别是$ {G_1} $和$ {G_2} $的距离矩阵, 则$ {G_1} \cong {G_2} $的充要条件是$ {f_\lambda }({D_1}) = {f_\lambda }({D_2}) $.
引理7[18]. 设$ C,\;B \in {{\bf{R}}^{n \times n}} $为对称矩阵, 对一切$ 1 \le i \le n $, $ {\lambda _i}(C) $为$ C $的特征值, $ {\lambda _i}(B) $为$ B $的特征值, 则$ \min {\lambda _i}(B) + {\lambda _i}(C) \le {\lambda _i}(C + B) $$ \le {\lambda _i}(C) \;+ \max {\lambda _i}(B) $.
设$ G = \left\langle {V,\;E} \right\rangle $是复杂无向连通图, $ V = \{ {v_1}, {v_2},\; \cdots ,\;{v_n}\} $, $ n \ge 2 $: 1) 除去$ G $中顶点上的自环和邻接顶点间的重边(邻接顶点间仅保留一条边), 可以得到一个简单无向连通图$ {G_1} $(称$ {G_1} $为$ G $的主图). 2) $ \forall i \ne j $, 若$ {v_i} $和$ {v_j} $邻接, 除去$ {v_i} $和$ {v_j} $之间的一条边, 其他保持不变, 可以得到另一个无向图$ {G_2} $(称$ {G_2} $为$ G $的附图). 3) 设$ A $为$ G $的邻接矩阵, $ {A_1} $和$ {A_2} $分别是$ {G_1} $和$ {G_2} $的邻接矩阵, $ D $为$ G $的距离矩阵. 由上述假设可知, $ A = {A_1} + {A_2} $. 因复杂无向图中的自环和顶点间的重边对距离没有影响, 由定义6和定义7可知, $ D $既是$ G $也是$ {G_1} $的距离矩阵.
基于以上的叙述和讨论, 本文给出两个复杂无向图同构的另一个判定条件.
定理3. 设$ {G_{\text{1}}} = \left\langle {{V_{\text{1}}},\;{E_{\text{1}}}} \right\rangle $和$ {G_{\text{2}}} = $$ \left\langle {{V_{\text{2}}},\;{E_{\text{2}}}} \right\rangle $是两个复杂无向连通图, 每个顶点最多有一个自环, $ \left| {{V_1}} \right| = \left| {{V_2}} \right| = n \ge {\text{2}} $, $ {A_1} $与$ {A_2} $分别是$ {G_1} $和$ {G_2} $的邻接矩阵, $ {D_1} $与$ {D_2} $分别是$ {G_1} $和$ {G_2} $的距离矩阵. 则$ {G_1} \cong {G_2} $的充要条件是$ {f_\lambda }({D_1}) = {f_\lambda }({D_2}) $且$ {f_\lambda }({A_1}) = {f_\lambda }({A_2}) $.
证明. 设$ {f_\lambda }({D_1}) = {f_\lambda }({D_2}) $且$ {f_\lambda }({A_1}) = $$ {f_\lambda }({A_2}) $. 另设$ {G_{11}} $与$ {G_{12}} $分别是$ {G_1} $的主图和附图, $ {A_{11}} $与$ {A_{12}} $$ ({A_{12}} \ne 0) $分别是$ {G_{11}} $和$ {G_{12}} $的邻接矩阵; $ {G_{21}} $与$ {G_{22}} $分别是$ {G_2} $的主图和附图, $ {A_{21}} $与$ {A_{22}} $$ ({A_{22}} \ne 0) $分别是$ {G_{21}} $和$ {G_{22}} $的邻接矩阵. 由此, 可得: $ {A_1} = {A_{11}} + {A_{12}} $, $ {A_2} = {A_{21}} + {A_{22}} $; $ {D_1} $既是$ {G_1} $也是$ {G_{11}} $的距离矩阵, $ {D_2} $既是$ {G_2} $也是$ {G_{21}} $的距离矩阵. 由引理6可知, 当$ {f_\lambda }({D_1}) = {f_\lambda }({D_2}) $时, $ {G_{11}} \cong {G_{21}} $; 再由引理2可知, 存在$ Q \in \Omega $, 使得$ {A_{11}} = {Q^{\text{T}}}{A_{21}}Q $. 因$ {A_1} $和$ {A_2} $均是实对称矩阵, 且$ {f_\lambda }({A_1}) = {f_\lambda }({A_2}) $, 由引理5可知, 存在$ n $阶正交矩阵$ P \in { T} $, 使得$ {A_1} = {P^{\text{T}}}{A_2}P $, 即$ {A_{11}} + {A_{12}} = {P^{\text{T}}}{A_{21}}P + {P^{\text{T}}}{A_{22}}P $. 综上可知, 当$ {f_\lambda }({D_1}) = {f_\lambda }({D_2}) $且$ {f_\lambda }({A_1}) = {f_\lambda }({A_2}) $时
$$ {A_{11}} = {Q^{\text{T}}}{A_{21}}Q $$ (1) 且
$$ {A_{11}} + {A_{12}} = {P^{\text{T}}}{A_{21}}P + {P^{\text{T}}}{A_{22}}P$$ (2) 设$ {A_{12}} = {P^{\text{T}}}{A_{22}}P $, 由式(1)和式(2)可得, $ {A_{11}} = {Q^{\text{T}}}{A_{21}}Q $, $ {A_{11}} = {P^{\text{T}}}{A_{21}}P $, 由此, $ P = Q $. 另由式(2)可得, $ {A_{11}} = {P^{\text{T}}}{A_{21}}P + {P^{\text{T}}}{A_{22}}P - {A_{12}} $.
1) 设$ {H_1} = {P^{\text{T}}}{A_{21}}P $, $ {H_2} = {P^{\text{T}}}{A_{22}}P - {A_{12}} $, 则
$${A_{11}} = {H_1} + {H_2} $$ (3) 因$ {H_1} $和$ {H_2} $均是实对称矩阵且$ \lambda ({H_1}) = \lambda ({A_{21}}) $. 由式(3)和引理7可得
$$ \begin{split} & \min {\lambda _i}({H_2}) + {\lambda _i}({A_{21}}) \le {\lambda _i}({A_{11}}) \le\\& \qquad{\lambda _i}({A_{21}}) +\max {\lambda _i}({H_2}) \end{split} $$ (4) 2) 设$ {A_{12}} \ne {P^{\text{T}}}{A_{22}}P $, 则$ {H_2} \ne 0 $. 因$ {H_2} $是对称矩阵, 故当$ {H_2} \ne 0 $时, $ \lambda ({H_2}) \ne 0 $. 设$ \min {\lambda _i}({H_2}) = \max {\lambda _i}({H_2}) = h $, 由式(4)可得, $ {\lambda _i}({A_{11}}) = {\lambda _i}({A_{21}}) \;+ h $. 若$ \lambda ({A_{11}}) = \lambda ({A_{21}}) $, 则$ h = 0 $, $ \lambda ({H_2}) = 0 $, $ {A_{12}} = {P^{\text{T}}}{A_{22}}P $, 与假设矛盾; 若$ \lambda ({A_{11}}) \ne \lambda ({A_{21}}) $, 则与式(1)矛盾. 设$ {\lambda _i}({A_{11}}) \le $$ {\lambda _i}({A_{21}}) + \max {\lambda _i}({H_2})\; ({\lambda _i}({A_{11}}) \ge {\lambda _i}({A_{21}}) + \min {\lambda _i}({H_2})) $, 若$ \lambda ({A_{11}}) \ne \lambda ({A_{21}}) $, 则与$ {A_{11}} = {Q^{\text{T}}}{A_{21}}Q $矛盾; 若$ \lambda ({A_{11}}) = \lambda ({A_{21}}) $, 则由引理5可得, $ {A_{11}} = {P^{\text{T}}}{A_{21}}P $$ (P \in { T}) $. 由此, ${A_{11}} = {P^{\text{T}}}{A_{21}}P,\; {A_{11}} = {Q^{\text{T}}}{A_{21}}Q $, $ P = Q $. 而当$ P = Q $时, 由式(1)和式(2)可得, $ {A_{12}} = {P^{\text{T}}}{A_{22}}P $, 与$ {A_{12}} \ne {P^{\text{T}}}{A_{22}}P $的假设矛盾. 总之, $ {A_{12}} \ne {P^{\text{T}}}{A_{22}}P $的假设不成立.
综上可知: 当$ {A_{12}} = {P^{\text{T}}}{A_{22}}P $时, $ P = Q $; 由式(2)可得$ {A_1} = {Q^{\text{T}}}{A_2}Q $, 再由引理2可得, $ {G_1} \cong {G_2} $.
设$ {G_1} \cong {G_2} $. 由引理2可知, 存在$ n $阶置换矩阵$ Q \in \Omega $, 使得$ {A_1} = {Q^{\text{T}}}{A_2}Q $. 因$ {G_1} $和$ {G_2} $均是复杂无向连通图, 如充分性证明可设, $ {A_1} = {A_{11}} + {A_{12}} $, $ {A_2} = {A_{21}} + {A_{22}} $, 由此, $ {A_{11}} + {A_{12}} = {Q^{\text{T}}}({A_{21}} + {A_{22}})Q $. 因$ Q $是正交矩阵, 故$ {f_\lambda }({A_1}) = {f_\lambda }({A_2}) $. 设$ {A_{11}} \ne {Q^{\text{T}}}{A_{21}}Q $, 则简单无向连通图$ {G_{11}} $和$ {G_{21}} $不同构, 进而可得$ {G_1} $和$ {G_2} $不同构, 与假设矛盾. 当$ {A_{11}} = {Q^{\text{T}}}{A_{21}}Q $时, 由引理2可知, $ {G_{11}} \cong {G_{21}} $; 再由引理6可得, $ {f_\lambda }({D_1}) = {f_\lambda }({D_2}) $. 综上, 当$ {G_1} \cong {G_2} $时, $ {f_\lambda }({D_1}) = {f_\lambda }({D_2}) $且$ {f_\lambda }({A_1}) = {f_\lambda }({A_2}) $.
□ 比较引理6和定理3可知, 简单无向连通图的同构条件不同于复杂无向连通图的同构条件.
由定理3的证明过程可知, 当定理3中的$ {G_1} $和$ {G_2} $均是简单无向连通图时, $ {G_1} = {G_{11}} $, $ {G_2} = {G_{21}} $, $ {A_{12}} = {A_{22}} = 0 $, $ {A_1} = {A_{11}} $, $ {A_2} = {A_{21}} $. 由引理6可知: 当$ {f_\lambda }({D_1}) = {f_\lambda }({D_2}) $时, $ {G_1} \cong {G_2} $; 再由引理2可知, 存在$ Q \in \Omega $, 使得$ {A_1} = {Q^{\text{T}}}{A_2}Q $, 进而可得$ {f_\lambda }({A_1}) = {f_\lambda }({A_2}) $. 由此, 当$ {G_1} $和$ {G_2} $均是简单无向连通图时, 定理3中的条件可简化为$ {f_\lambda }({D_1}) = {f_\lambda }({D_2}) $; 定理3退化为引理6. 这表明定理3也适合简单无向连通图.
因为求解距离矩阵$ D $的算法复杂度是$ {\mathrm{O}}({n^3}) $[12−13], 求解特征多项式的算法复杂度是$ {\mathrm{O}}({n^3}) $[16−17], 故定理3判定条件的算法复杂度是$ 4{\mathrm{O}}({n^3}) $.
设$ {G_1} $和$ {G_2} $是两个复杂无向不连通图且分别由$ m $个连通子图$ {G_{ij}} $$ (i = 1,\;2;{\text{ }}1 \le j \le m) $组成, $ {G_1} $与$ {G_2} $同构是指$ {G_1} $中的连通子图$ {G_{1j}} $与$ {G_2} $中的连通子图$ {G_{2j}} $一一对应同构. 不难理解, 将定理3用于复杂无向不连通图的各个连通子图, 就可解决复杂无向不连通图的同构判定问题.
比较定理2和定理3可知: 1) 定理2适合一切无向图, 而定理3仅适合复杂无向连通图; 2) 若将定理2限定在复杂无向连通图上, 则定理2与定理3等价; 3) 就一般复杂无向图的同构判定问题而言, 定理2比定理3具有更低的算法复杂度, 因此也更便于实际应用.
1) $ {G_1} $和$ {G_2} $均是复杂无向连通图. 设$ {G_1} $和$ {G_2} $的邻接矩阵分别是$ {A_{11}} $和$ {A_{12}} $, 距离矩阵分别是$ {D_1} $和$ {D_2} $. 按图中顶点标号, 经计算可得
$$ {A_{11}} = \left[ {\begin{array}{*{20}{c}} 1&1&1 \\ 1&1&1 \\ 1&1&1 \end{array}} \right] ,\; {A_{12}} = \left[ {\begin{array}{*{20}{c}} 1&1&1 \\ 1&0&2 \\ 1&2&0 \end{array}} \right] $$ $$ {D_1} = {D_2} = \left[ {\begin{array}{*{20}{c}} 0&1&1 \\ 1&0&1 \\ 1&1&0 \end{array}} \right] $$ $$ {f_\lambda }({A_{11}} + {A_3}) = {\lambda ^3} - 3{\lambda ^2} - 9\lambda - 5\qquad\qquad $$ $$ {f_\lambda }({A_{12}} + {A_3}) = {\lambda ^3} - {\lambda ^2} - 17\lambda - 15 \qquad\quad\;\;$$ $$ {f_\lambda }({A_{11}}) = {\lambda ^3} - 3{\lambda ^2}, {f_\lambda }({A_{12}}) = {\lambda ^3} - {\lambda ^2} - 6\lambda$$ 其中, $ {A_3} $是3顶点无向完全图的邻接矩阵.
因$ {f_\lambda }({A_{11}} + {A_3}) \ne {f_\lambda }({A_{12}} + {A_3}) $, 由定理2可以判定$ {G_1} $和$ {G_2} $不同构. 因$ {f_\lambda }({D_1}) = {f_\lambda }({D_2}) $, 但$ {f_\lambda }({A_{11}}) \ne {f_\lambda }({A_{12}}) $, 由推论1和定理3均可判定$ {G_1} $和$ {G_2} $不同构.
2) $ {G_3} $和$ {G_4} $均是复杂无向连通图. 设$ {G_3} $的邻接矩阵和距离矩阵分别是$ {A_{31}} $和$ {D_3} $, $ {G_4} $的邻接矩阵和距离矩阵分别是$ {A_{41}} $和$ {D_4} $. 按图中顶点标号, 经计算可得
$$ {A_{31}} = {A_{41}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&1&1&1 \\ 0&0&0&0&2&0&1&1 \\ 0&0&0&1&0&1&0&1 \\ 0&0&1&0&1&0&1&0 \\ 0&2&0&1&0&1&0&0 \\ 1&0&1&0&1&0&0&0 \\ 1&1&0&1&0&0&0&0 \\ 1&1&1&0&0&0&0&0 \end{array}} \right] $$ $$ {D_3} = {D_4} = \left[ {\begin{array}{*{20}{c}} 0&2&2&2&2&1&1&1 \\ 2&0&2&2&1&2&1&1 \\ 2&2&0&1&2&1&2&1 \\ 2&2&1&0&1&2&1&2 \\ 2&1&2&1&0&1&2&2 \\ 1&2&1&2&1&0&2&2 \\ 1&1&2&1&2&2&0&2 \\ 1&1&1&2&2&2&2&0 \end{array}} \right] $$ 设$ {A_8} $是8顶点无向完全图的邻接矩阵. 因$ {f_\lambda }({A_{31}} + {A_8}) = {f_\lambda }({A_{41}} + {A_8}) $, 由定理2可以判定$ {G_3} \cong {G_4} $. 因$ {f_\lambda }({D_3}) = {f_\lambda }({D_4}) $且$ {f_\lambda }({A_{31}}) = $$ {f_\lambda }({A_{41}}) $, 故由定理3亦可判定$ {G_3} \cong {G_4} $.
3) $ {G_5} $和$ {G_6} $均是复杂无向连通图. 设$ {G_5} $的邻接矩阵和距离矩阵分别是$ {A_{51}} $和$ {D_5} $, $ {G_6} $的邻接矩阵和距离矩阵分别是$ {A_{61}} $和$ {D_6} $. 按图中顶点标号, 经计算可得
$$ {A_{51}} = {A_{61}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&1&1&1 \\ 0&0&0&1&1&1 \\ 0&0&0&1&1&2 \\ 1&1&1&0&0&0 \\ 1&1&1&0&0&0 \\ 1&1&2&0&0&0 \end{array}} \right] $$ $$ {D_5} = {D_6} = \left[ {\begin{array}{*{20}{c}} 0&2&2&1&1&1 \\ 2&0&2&1&1&1 \\ 2&2&0&1&1&1 \\ 1&1&1&0&2&2 \\ 1&1&1&2&0&2 \\ 1&1&1&2&2&0 \end{array}} \right] $$ 设$ {A_6} $是6顶点无向完全图的邻接矩阵. 因$ {f_\lambda }({A_{51}} + {A_6}) = {f_\lambda }({A_{61}} + {A_6}) $, 由定理2可以判定$ {G_5} \cong {G_6} $. 因$ {f_\lambda }({A_{51}}) = {f_\lambda }({A_{61}}) $且$ {f_\lambda }({D_5}) = $$ {f_\lambda }({D_6}) $, 由定理3亦可判定$ {G_5} \cong {G_6} $.
4) $ {G_7} $和$ {G_8} $均是无向树. 设$ {G_7} $和$ {G_8} $的邻接矩阵分别是$ {A_{71}} $和$ {A_{81}} $, 距离矩阵分别是$ {D_7} $和$ {D_8} $. 按图中顶点标号, 经计算可得
$$ {A_{71}} = \left[ {\begin{array}{*{20}{c}} 0&1&1&1&1&0&0&0 \\ 1&0&0&0&0&1&1&1 \\ 1&0&0&0&0&0&0&0 \\ 1&0&0&0&0&0&0&0 \\ 1&0&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0 \end{array}} \right] \; $$ $$ {A_{81}} = \left[ {\begin{array}{*{20}{c}} 0&1&1&1&1&1&0&0 \\ 1&0&0&0&0&0&0&0 \\ 1&0&0&0&0&0&0&0 \\ 1&0&0&0&0&0&0&0 \\ 1&0&0&0&0&0&0&0 \\ 1&0&0&0&0&0&1&0 \\ 0&0&0&0&0&1&0&1 \\ 0&0&0&0&0&0&1&0 \end{array}} \right] $$ $$ {D_7} = \left[ {\begin{array}{*{20}{c}} 0&1&1&1&1&2&2&2 \\ 1&0&2&2&2&1&1&1 \\ 1&2&0&2&2&3&3&3 \\ 1&2&2&0&2&3&3&3 \\ 1&2&2&2&0&3&3&3 \\ 2&1&3&3&3&0&2&2 \\ 2&1&3&3&3&2&0&2 \\ 2&1&3&3&3&2&2&0 \end{array}} \right] $$ $$ {D_8} = \left[ {\begin{array}{*{20}{c}} 0&1&1&1&1&1&2&3 \\ 1&0&2&2&2&2&3&4 \\ 1&2&0&2&2&2&3&4 \\ 1&2&2&0&2&2&3&4 \\ 1&2&2&2&0&2&3&4 \\ 1&2&2&2&2&0&1&2 \\ 2&3&3&3&3&1&0&1 \\ 3&4&4&4&4&2&1&0 \end{array}} \right] $$ 设$ {A_8} $是8顶点无向完全图的邻接矩阵, 可得$ \det ({A_{71}} + {A_8}) = 17 $, $ \det ({A_{81}} + {A_8}) = 21 $. 由此, $ {f_\lambda }({A_{71}} + {A_8}) \ne {f_\lambda }({A_{81}} + {A_8}) $, 由定理2可以判定$ {G_7} $和$ {G_8} $不同构. 另外, 还可求得: $ {f_\lambda }({A_{71}}) = {f_\lambda }({A_{81}}) = {\lambda ^8} - 7{\lambda ^6} + 9{\lambda ^4} $; $ \det ({D_7}) = $$- 1\,048$, $\det ({D_8}) = 1\,600$. 因$ \det ({D_7}) \ne \det ({D_8}) $, 故$ {f_\lambda }({D_7}) \ne {f_\lambda }({D_8}) $. 由此, $ {f_\lambda }({A_{71}}) = {f_\lambda }({A_{81}}) $, 但$ {f_\lambda }({D_7}) \ne {f_\lambda }({D_8}) $, 由定理3可以判定$ {G_7} $和$ {G_8} $不同构.
3. 结束语
图的同构关系是一种等价关系, 凡与图的结构相关的分类、聚类、识别和学习等问题均与图的同构判定问题有关. 时至今日, 图的同构判定问题仍然具有重要的理论和应用价值.
文献[10]将基于邻接矩阵的同构判定条件(引理2)推广到简单无向图距离矩阵(引理6和引理7), 解决了简单无向图的同构判定问题. 但引理6和引理7不能用于复杂无向图的同构判定, 原因在于复杂无向图的同构关系不能由其距离矩阵唯一确定.
本文的主要思路和贡献可概括为: 1) 证明了对角线元素为0或1而其他元素均为正整数的对称矩阵在非同构正交变换下不再是非负整数对称矩阵(定理1); 利用无向完全图邻接矩阵在矩阵同构变换下保持不变的特性, 给出了引理2的另一种等价表示(推论2); 基于定理1和推论2, 给出了基于邻接矩阵之和的特征多项式判定条件(定理2). 2) 针对复杂无向连通图的同构判定问题, 使用图及邻接矩阵的分解方法, 给出了基于邻接矩阵特征多项式和距离矩阵特征多项式的同构判定条件(定理3). 将该条件用于复杂无向不连通图的各个连通子图, 就可解决复杂无向不连通图的同构判定问题. 定理2和定理3中的判定条件均是充要条件且均具有多项式时间复杂度. 需要再次说明的是: 定理2所给的判定条件具有一般普适性, 即对任意的简单、复杂(每一顶点最多允许有一个自环)、连通和不连通无向图均适用; 定理3既适合复杂无向连通图也适合简单无向连通图.
与文献[10]中的结果相比, 定理2和定理3是无向图同构研究方面的又一重要进展. 定理2和定理3的另一理论价值表明, 无向图的同构判定问题是 P 问题. 需要说明的是, 虽然我们解决了无向图的同构判定问题, 但有向图的同构判定是 P 问题还是 NP 问题仍然没有得到解决.
今后我们将针对有向图的同构判定问题开展研究, 期望得到一些有理论和实用价值的新结果.
-
图 2 中心点和近邻点的局部结构图
Fig. 2 Diagram of local structure between the central point and its neighbors
图 7 采样密度实验结果对比
Fig. 7 Comparison of experiment results with different sampling densities
表 1 实验配置
Table 1 Experimental configuration
项目 详情 操作系统 CentOS Linux7 GPU Tesla V100 32 GB CUDA 10.0 CUDNN 7.0 Python 3.6.0 Pytorch 1.3.0 
下载: 导出CSV
表 2 在ModelNet40数据集上的实验结果
Table 2 Experimental results on ModelNet40
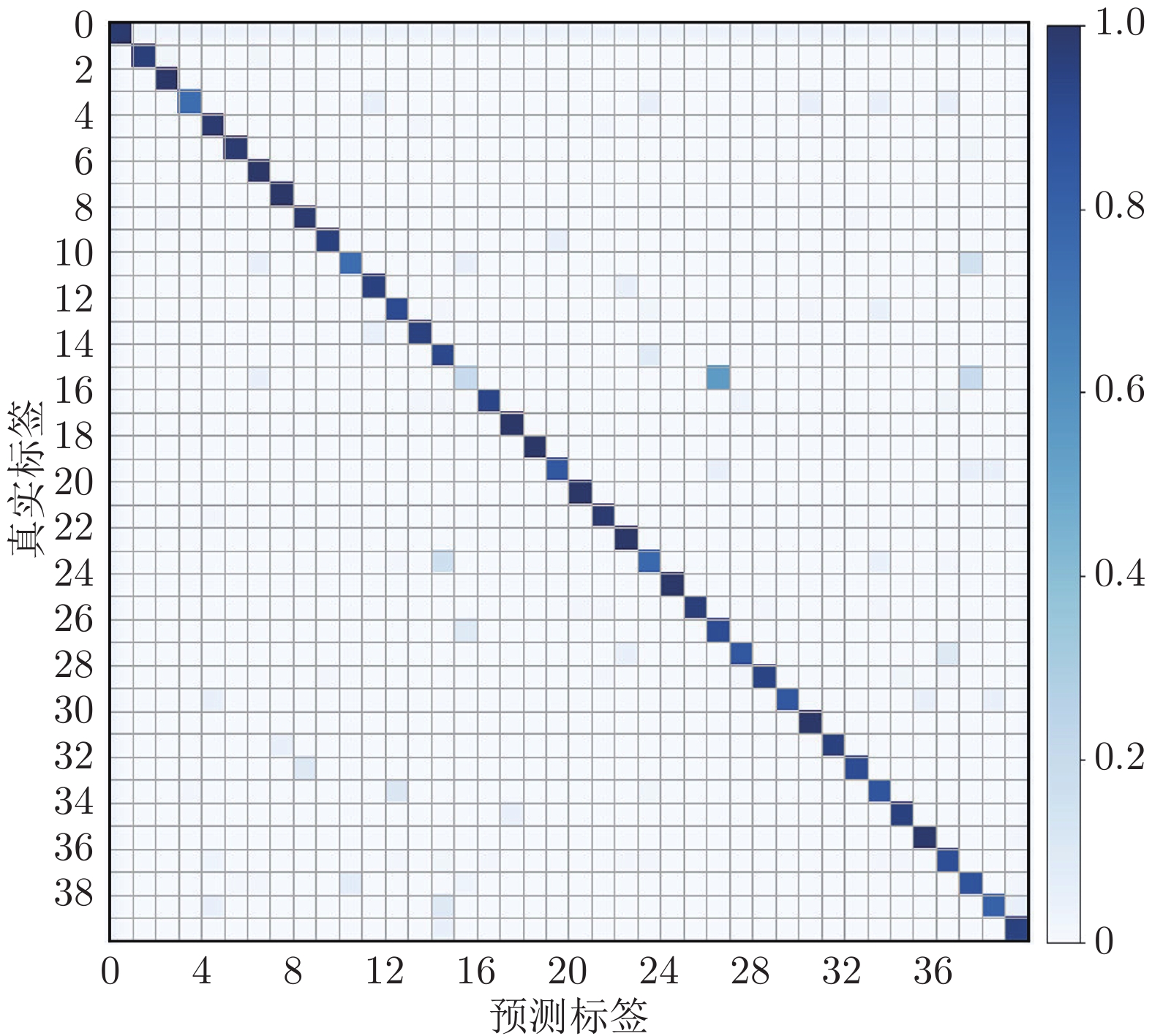
方法 输入 mAcc (%) OA (%) PointNet 1 k 86.0 89.2 PointNet++ 1 k — 90.7 Spec-GCN 1 k — 91.5 DGCNN 1 k 90.2 92.9 RSCNN 1 k — 92.9 PCT 1 k — 93.2 ECC[22] 1 k 83.2 87.4 RMFP-DNN[23] 1 k 88.9 92.6 PointCNN[24] 1 k 88.1 92.2 Point2sequence[25] 1 k 90.4 92.6 Point Transformer [26] 1 k — 92.8 Octant-CNN[27] 1 k 88.7 91.9 DRNet[28] 1 k — 93.1 AdaptConv[29] 1 k 90.7 93.4 RFNet 1 k 91.2 93.6 PointNet++ 5 k + nor — 91.9 DGCNN 2 k 90.7 93.5 RSCNN 1 k + voting — 93.6 SpiderCNN 5 k + nor — 92.4 RFNet 2 k 91.4 94.0
下载: 导出CSV
表 3 不同网络的易错模型分类对比
Table 3 Classification comparison of error-prone models for different networks
易错模型 真实标签 PointNet DGCNN RFNet 
植物 植物 植物 植物 
花盆 植物 植物 植物 
花瓶 花盆 花瓶 花瓶 
花瓶 瓶子 花瓶 花瓶 
杯子 花盆 花盆 杯子
下载: 导出CSV
表 4 在ShapeNetCore数据集上的实验结果
Table 4 Experimental results on ShapeNetCore
方法 输入 OA (%) PointNet 1 k 83.7 PointNet++ 1 k 85.1 DGCNN 1 k 84.7 Point2sequence 1 k 85.2 SpiderCNN 1 k + nor 85.3 KPConv[30] 1 k 86.2 RFNet 1 k 88.3
下载: 导出CSV
表 5 在ScanObjectNN数据集上的实验结果 (%)
Table 5 Experimental results on ScanObjectNN (%)
方法 mAcc OA Bag Bin Box Sofa Desk Shelf Table Door Bed Cabinet Chair Display Pillow Sink Toilet PointNet 63.4 68.2 36.1 69.8 10.5 76.7 50.0 72.6 67.8 93.8 61.8 62.6 89.0 73.0 67.6 64.2 55.3 PointNet++ 75.4 77.9 49.4 84.4 31.6 90.5 74.0 72.6 72.6 85.2 75.5 77.4 91.3 79.4 81.0 80.8 85.9 DGCNN 73.6 78.1 49.4 82.4 33.1 91.4 63.3 79.3 77.4 89.0 64.5 83.9 91.8 77.0 77.1 75.0 69.4 PointCNN 75.1 78.5 57.8 82.9 33.1 91.9 65.3 84.2 67.4 84.8 80.0 83.6 92.6 78.4 80.0 72.5 71.8 SpiderCNN 69.8 73.7 43.4 75.9 12.8 90.5 65.3 78.0 65.9 91.4 69.1 74.2 89.0 74.5 80.0 65.8 70.6 RFNet 76.3 79.6 54.0 81.9 34.1 92.2 74.1 79.9 72.1 91.5 81.3 83.5 91.3 80.2 82.6 78.9 67.0
下载: 导出CSV
表 6 不同模块的消融实验 (%)
Table 6 Ablation experiment of different modules (%)
方法 RFConv WAP JL mAcc OA 网络0 × × × 90.2 92.9 网络1 √ × × 91.0 93.3 网络2 √ √ × 91.1 93.5 网络3 √ × √ 91.1 93.4 网络4 √ √ √ 91.2 93.6
下载: 导出CSV
表 7 高斯噪声鲁棒性实验 (%)
Table 7 Robustness experiment of Gaussian noise (%)
方法 无高斯噪声 有高斯噪声 mAcc OA mAcc OA PointNet 86.0 89.2 83.4 87.6 PointNet++ — 90.7 — 89.6 DGCNN 90.2 92.9 89.7 92.6 RSCNN — 92.9 — 92.3 RFNet 91.2 93.6 91.0 93.5
下载: 导出CSV
表 8 不同特征关系的消融实验 (%)
Table 8 Ablation studies about different relationships between features (%)
方法 ${e_{ij}}$ $di{s_{ij}}$ ${l_{ij}}$ ${s_{ij}}$ OA 网络1 √ × × × 93.3 网络2 √ × √ × 93.5 网络3 √ × √ √ 93.6 网络4 √ √ × × 93.1 网络5 × √ √ √ 93.5 网络6 √ √ √ √ 93.2
下载: 导出CSV
表 9 网络的复杂度对比
Table 9 Comparison of network complexity
方法 参数量(M) 浮点运算数(G) OA (%) PointNet 3.47 0.45 89.2 PointNet++ 1.74 4.09 91.9 DGCNN 1.81 2.43 92.9 PCT 2.88 2.32 93.2 KPConv 14.30 — 92.9 RFNet 2.36 2.95 93.6
下载: 导出CSV
-
[1] Guo Y, Bennamoun M, Sohel F, Min L, Wan J. 3D object recognition in cluttered scenes with local surface features: a survey. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2014, 36(11): 2270-2287 [2] 田永林, 沈宇, 李强, 王飞跃. 平行点云: 虚实互动的点云生成与三维模型进化方法. 自动化学报, 2020, 46(12): 2572-2582Tian Yong-Lin, Shen Yu, Li Qiang, Wang Fei-Yue. Parallel point clouds: point clouds generation and 3d model evolution via virtual-real interaction. Acta Automatica Sinica, 2020, 46(12): 2572-2582 [3] Qi C R, Su H, Mo K, Guibas L J. PointNet: Deep learning on point sets for 3D classification and segmentation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE, 2017. 77−85 [4] Guo Y, Wang H, Hu Q, Liu H, Bennamoun M. Deep learning for 3d point clouds: a survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020. 43(12): 4438-4364 [5] Su H, Maji S, Kalogerakis E, Learned-Miller E. Multi-view convolutional neural networks for 3D shape recognition. In: Proceedings of the IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015. 945−953 [6] Yang Z, Wang L. Learning relationships for multi-view 3D object recognition. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul, South Korea: IEEE, 2019. 7504−7513 [7] 徐思雨, 祝继华, 田智强, 李垚辰, 庞善民. 逐步求精的多视角点云配准方法. 自动化学报, 2019, 45(8): 1486-1494Xu Si-Yu, Zhu Ji-Hua, Tian Zhi-Qiang, Li Yao-Chen, Pang Shan-Min. Stepwise refinement approach for registration of multi-view point sets. Acta Automatica Sinica, 2019, 45(8): 1486-1494 [8] Maturana D, Scherer S. VoxNet: A 3D convolutional neural network for real-time object recognition. In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Hamburg, Germany: IEEE, 2015. 922−928 [9] Riegler G, Osman U A, Geiger A. OctNet: Learning deep 3D representations at high resolutions. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE, 2017. 6620−6629 [10] Qi C R, Yi L, Su H, Guibas L J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In: Proceedings of the Advances in Neural Information Processing Systems. Long Beach, USA: 2017. 5099−5108 [11] Wang C, Samari B, Siddiqi K. Local spectral graph convolution for point set feature learning. In: Proceedings of the European Conference on Computer Vision. Munich, Germany: 2018. 56−71 [12] Wang Y, Sun Y, Liu Z, Sarma S E, Bronstein M M, Solomon J M. Dynamic graph cnn for learning on point clouds. ACM Transactions on Graphics, 2019, 38(5): 1-12 [13] Liu Y, Fan B, Xiang S, Pan C. Relation-shape convolutional neural network for point cloud analysis. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, USA: IEEE, 2019. 8895−8904 [14] Wang L, Huang Y, Hou Y, Zhang S, Shan J. Graph attention convolution for point cloud semantic segmentation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, USA: IEEE, 2019. 10288−10297 [15] Chen C, Fragonara L Z, Tsourdos A. Gapointnet: graph attention based point neural network for exploiting local feature of point cloud. Neurocomputing, 2021, 438: 122-132 doi: 10.1016/j.neucom.2021.01.095 [16] Guo M H, Cai J X, Liu Z N, Mu T J, Martin R R, Hu S M. Pct: point cloud transformer. Computational Visual Media, 2021, 7(2): 187-299 doi: 10.1007/s41095-021-0229-5 [17] Wen Y, Zhang K, Li Z, Qiao Y. A discriminative feature learning approach for deep face recognition. In: Proceedings of the European Conference on Computer Vision. Amsterdam, Netherland: 2016. 499−515 [18] Wu Z, Song S, Khosla A, Yu F, Zhang L, Tang X, et al. 3D ShapeNets: A deep representation for volumetric shapes. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Boston, USA: IEEE, 2015. 1912−1920 [19] Yi L, Kim V G, Ceylan D, Shen I C, Yan M, Su H, et al. A scalable active framework for region annotation in 3d shape collections. ACM Transactions on Graphics, 2016, 35(6): 1-12 [20] Uy M A, Pham Q H, Hua B S, Nguyen T, Yeung S K. Revisiting point cloud classification: A new benchmark data-set and classification model on real-world data. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul, South Korea: IEEE, 2019. 1588−1597 [21] Xu Y, Fan T, Xu M, Long Z, Yu Q. SpiderCNN: Deep learning on point sets with parameterized convolutional filters. In: Proceedings of the European Conference on Computer Vision. Munich, Germany: 2018. 90−105 [22] Simonovsky M, Komodakis N. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE, 2017. 3693−3702 [23] 田钰杰, 管有庆, 龚锐. 一种鲁棒的多特征点云分类分割深度神经网络. 计算机工程, 2021, 47(11): 234-240Tian Yu-Jie, Guan You-Qing, Gong Rui. A robust deep neural network for multi-feature point cloud classification and segmentation. Computer Engineering, 2021, 47(11): 234-240 [24] Li Y, Bu R, Sun M, Chen B. PointCNN: Convolution on x-transformed points. In: Proceedings of the Advances in Neural Information Processing System. Montreal, Canada: 2018. 828− 838 [25] Liu X, Han Z, Liu Y, Zwicker M. Point2sequence: Learning the shape representation of 3D point clouds with an attention-based sequence to sequence network. In: Proceedings of the AAAI Conference on Artificial Intelligence. Honolulu, USA: AAAI, 2019. 8778−8785 [26] Engel N, Belagiannis V, Dietmayer K. Point transformer. IEEE Access, 2021, 9: 134826-134840 doi: 10.1109/ACCESS.2021.3116304 [27] 许翔, 帅惠, 刘青山. 基于卦限卷积神经网络的3D点云分析. 自动化学报, 2021, 47(12): 2791−2800Xu Xiang, Shuai Hui, Liu Qing-Shan. Octant convolutional neural network for 3D point cloud analysis. Acta Automatica Sinica, 2021, 47(12): 2791−2800 [28] Qiu S, Anwar S, Barnes N. Dense-resolution network for point cloud classification and segmentation. In: Proceedings of the IEEE Winter Conference on Applications of Computer Vision. Virtual Event: IEEE, 2021. 3812−3821 [29] Zhou H, Feng Y, Fang M, Wei M, Qin J, Lu T. Adaptive graph convolution for point cloud analysis. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. Montreal, Canada: IEEE, 2021. 4965−4974 [30] Thomas H, Qi C R, Deschaud J E, Marcotegui B, Goulette F, Guibas L. KPConv: Flexible and deformable convolution for point clouds. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul, South Korea: IEEE, 2020. 6420−6429 -
下载:
计量
- 文章访问数: 1434
- HTML全文浏览量: 539
- PDF下载量: 298
- 被引次数: 0
