-
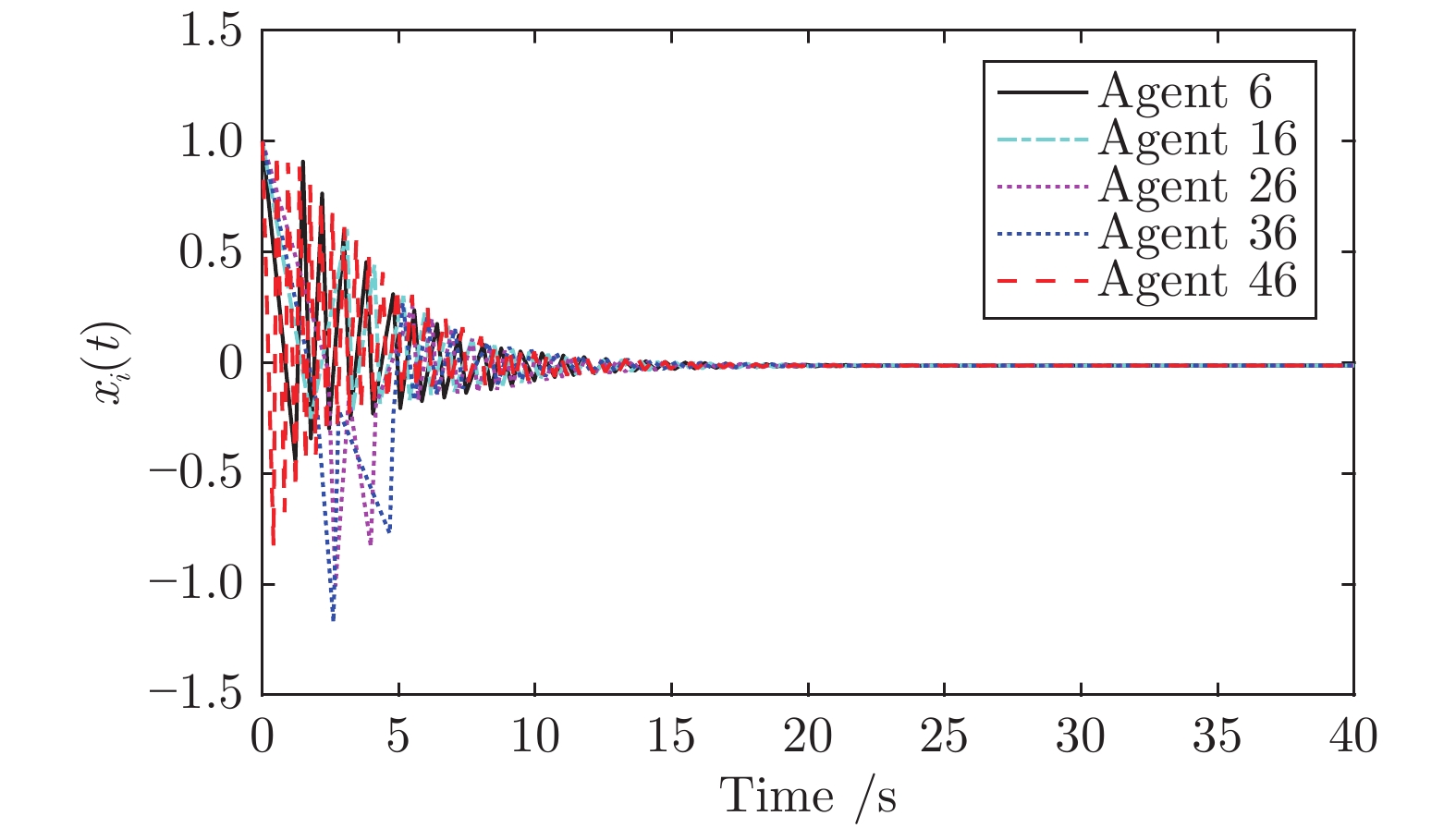
摘要: 本文研究了一类分布式优化问题, 其目标是通过局部信息交换使由局部成本函数之和构成的全局成本函数最小. 针对无向连通图, 我们提出了两种基于比例积分策略的分布式优化算法. 在局部成本函数可微且凸的条件下, 证明了所提算法渐近收敛到全局最小值点. 更进一步, 在局部成本函数具有局部Lipschitz梯度和全局成本函数关于全局最小值点是有限强凸的条件下, 证明了所提算法的指数收敛性. 此外, 为了避免智能体之间的连续通信和减少通信负担, 将所提的两种分布式优化算法与事件触发通信相结合, 提出了两种基于事件触发的分布式优化算法. 证明了提出的事件触发优化算法不存在Zeno行为, 并且在相应条件下保持了与连续通信下分布式优化算法一样的收敛性. 最后, 通过数值仿真验证了上述理论结果.Abstract: This paper studies a class of distributed optimization problems, whose objective is to minimize the global cost function formed by a sum of local cost functions through local information exchanges. For undirected connected graphs, we propose two distributed optimization algorithms based on the proportional-integral feedback mechanism. Under the condition that the local cost functions are differentiable and convex, it is proved that the proposed algorithms asymptotically converge to a global minimum. For the case that the local cost functions have local Lipschitz gradient and the global cost function is strongly convex with respect to the global minimum, the exponential convergences of the two distributed optimization algorithms are established. In addition, in order to avoid continuous communication between agents and reduce communication burden, by integrating the two proposed distributed optimization algorithms with event-triggered communications, two event-triggered based distributed optimization algorithms are developed. It is shown that the two proposed event-triggered optimization algorithms are free of Zeno behavior. Moreover, the two proposed event-triggered based distributed optimization algorithms maintain the same convergence properties as the distributed optimization algorithms with continuous communications under the corresponding conditions. Finally, the above theoretical results are verified by numerical simulations.
-
全源导航系统中传感器种类和数量繁多, 在进行导航时要使用多个传感器的数据来进行组合导航. 如果传感器发生故障, 那么将会引起导航解算错误. 因此, 在进行导航解算前, 必须先对传感器进行故障检测.
故障检测方向一直有许多学者研究, 主要分为两种方法. 一种方法是建立对应的数学模型, 根据系统状态量之间的关系来判断传感器是否发生故障. 如张绍杰等[1]、Avram等[2]、汤文涛等[3]、Sadeghzadeh-Nokhodberiz等[4]都是先建立系统的数学模型, 然后对系统的误差特性进行分析, 进而实现故障诊断. 该方法比较复杂, 需要了解系统的工作原理, 但实际中许多系统难以抽象出数学模型, 因此应用范围比较小.
另一种方法是基于人工智能方法, 其采用特征工程与机器学习方法或深度学习进行故障诊断. Yan等[5]、Swischuk等[6]和郑晓飞等[7]先采用特征工程进行信息提取, 然后采用机器学习方法进行识别; Jing等[8]和Guo等[9]采用深度学习的方法对原始数据进行故障检测. 一方面特征工程比较复杂; 另一方面这些方法都侧重于对单个传感器数据的故障诊断, 且难以准确识别出间歇性故障和渐变性故障.
针对以上研究中出现的问题, 本文基于导航数据预处理平台[10], 提出了一种基于多阶段注意力机制的编码器−解码器(Encoder-decoder)模型算法, 该算法可以利用多类传感器数据之间的关系进行传感器的状态互检测, 不仅可以准确检测出故障传感器, 并且可以检测出其故障类型.
1. 问题研究
1.1 问题分析
全源导航系统中有多类型、多数量的传感器, 如光纤陀螺、加速度计、GPS接收机、高度计、磁力罗盘、相机和激光雷达等, 每个传感器都会产生出大量的数据, 如加速度、相对速度、绝对速度、角速率、位移、经纬度和高度等.
在载体坐标系下, 载体的加速度、相对速度、绝对速度、位移、经度、纬度和高度存在着一定的关系. 根据组合导航基本原理[11], 多数导航系统都是以惯性导航传感器为主, 与其余类型传感器组合进行导航. 因此, 当一个传感器出现故障时, 可以利用其余的传感器数据来进行辅助判断. 本文的研究目的是根据多个传感器数据的输入进行故障互检测, 不仅要检测出故障传感器, 也要识别出其故障类型.
1.2 数据说明
假设有
$n$ 个传感器数据, 每个传感器数据经过时间同步后在单位时间内产生等数量的数据. 本文中设输入${\boldsymbol{x}} = {\left( {{x^1},{x^2}, \cdots ,{x^n}} \right)^ {{\rm{T}}} } = \left( {{x_1},{x_2}, \cdots ,{x_T}} \right) \in$ ${{\bf{R}}^{n \times T}},$ 其中$T$ 为时间窗口, 表示每一类传感器数据的个数. 本文采用${{\boldsymbol{x}}^k} = \left( {x_1^k,x_2^k, \cdots ,x_T^k} \right) \in {{\bf{R}}^T}$ 表示同一类传感器数据在$T$ 时间段内的数据, 采用${{\boldsymbol{x}}_t} = $ $ \left( {x_t^1,x_t^2, \cdots ,x_t^n} \right) \in {{\bf{R}}^n}$ 表示在同一时刻的$n$ 个传感器数据.对于目标传感器数据的状态, 本文利用其余传感器数据来判断其数据是否出错. 即对于输入
$x ,$ 要判断这组输入数据的状态$\hat y$ :$$\hat y = f({x_1},{x_2}, \cdots, {x_T})$$ (1) 其中,
$f(\cdot )$ 是要学习的非线性关系.传感器数据是时间序列数据, 在时间维度上存在相互依赖性, 而循环神经网络(Recurrent neural network, RNN)具有记忆性, 可以高效地捕捉序列数据在时间上的相互依赖性, 进而对序列数据的非线性特征进行学习, 因此采用循环神经网络来拟合其非线性关系.
2. 基于循环神经网络的故障诊断分析
循环神经网络是一类以序列数据为输入, 在序列的演进方向进行递归且所有循环单元按链式连接的递归神经网络. 循环神经网络具有记忆性, 且可以参数共享和图灵完备, 因此能以很高的效率对序列的非线性特征进行学习.
传统的循环神经网络具有长期依赖问题, 无法捕捉长时间跨度的非线性关系. 长短期记忆网络(Long-short-term memory, LSTM)[12]增加了3个控制单元来对输入数据进行非线性变换, 解决了传统循环神经网络单元会出现的长期依赖问题.
针对本文的多传感器故障诊断任务, 其故障类型有间歇型、渐变型和阶跃型三种故障类型. 其中间歇型故障没有明确的模式和频率, 随机地出现和消失; 渐变型故障对数据的影响随着时间推移而增大, 在故障早期难以发现. LSTM单元虽然可以准确地捕捉传感器数据在时间上的相互依赖性, 从而判断出数据状态; 但由于间歇型和渐变型故障的复杂性, 仅仅使用LSTM单元会造成一定程度的误判. 为了解决该问题, 本文采用基于注意力机制[13]的编码器−解码器(Encoder-decoder)[14]结构.
一方面, 采用注意力机制可以捕捉到输入数据在空间维度和时间维度上的内在关系, 从而对输入进行重构, 使模型可以更好地学习输入数据之间的相互关系; 另一方面, 编码器−解码器结构中编码器将输入数据编码成状态向量, 解码器将状态向量解码后传输给多层感知机[15]进行分类处理, 该结构在产生每一个输出的时候, 能够充分利用输入序列携带的信息, 可以降低过拟合现象, 提高模型的整体性能.
综上分析, 对于多传感器故障诊断任务, 本文采用基于注意力机制的编码器−解码器结构来实现, 该结构以LSTM为基本单元, 采用多阶段的注意力机制来构建数据之间的相互关系, 其输出经过多层感知机进行分类, 进而判断出传感器的数据状态.
3. 多阶段注意力机制研究
对于多传感器故障诊断任务, 本文从传感器的空间维度和时间维度来研究. 在传感器的空间维度上, 每种类型的传感器数据在同一时刻具有相互依赖性; 在时间维度上, 每一类的传感器数据在不同时间段的数据对其余时间段的数据的状态贡献程度不一样; 因此可以从这两个角度来判断传感器的数据状态. 本文设计的基于多阶段注意力的编码器−解码器结构如图1所示. 首先, 将多传感器的数据传送给局部注意力和全局注意力机制, 用于捕捉传感器数据在空间和时间维度上的相互依赖性; 然后将数据传输给带有时间注意力机制的编码器—解码器模型, 其中编码器−解码器用于对数据进行状态编码和状态解码, 时间注意力机制是为了防止编码器−解码器模型的性能会随着输入数据的长度而急剧衰减; 将解码后的状态信息传输给多层感知机进行分类, 根据分类结果就可以确定出故障传感器和故障类别.
3.1 局部注意力研究
对于所有的传感器数据, 每个传感器数据在
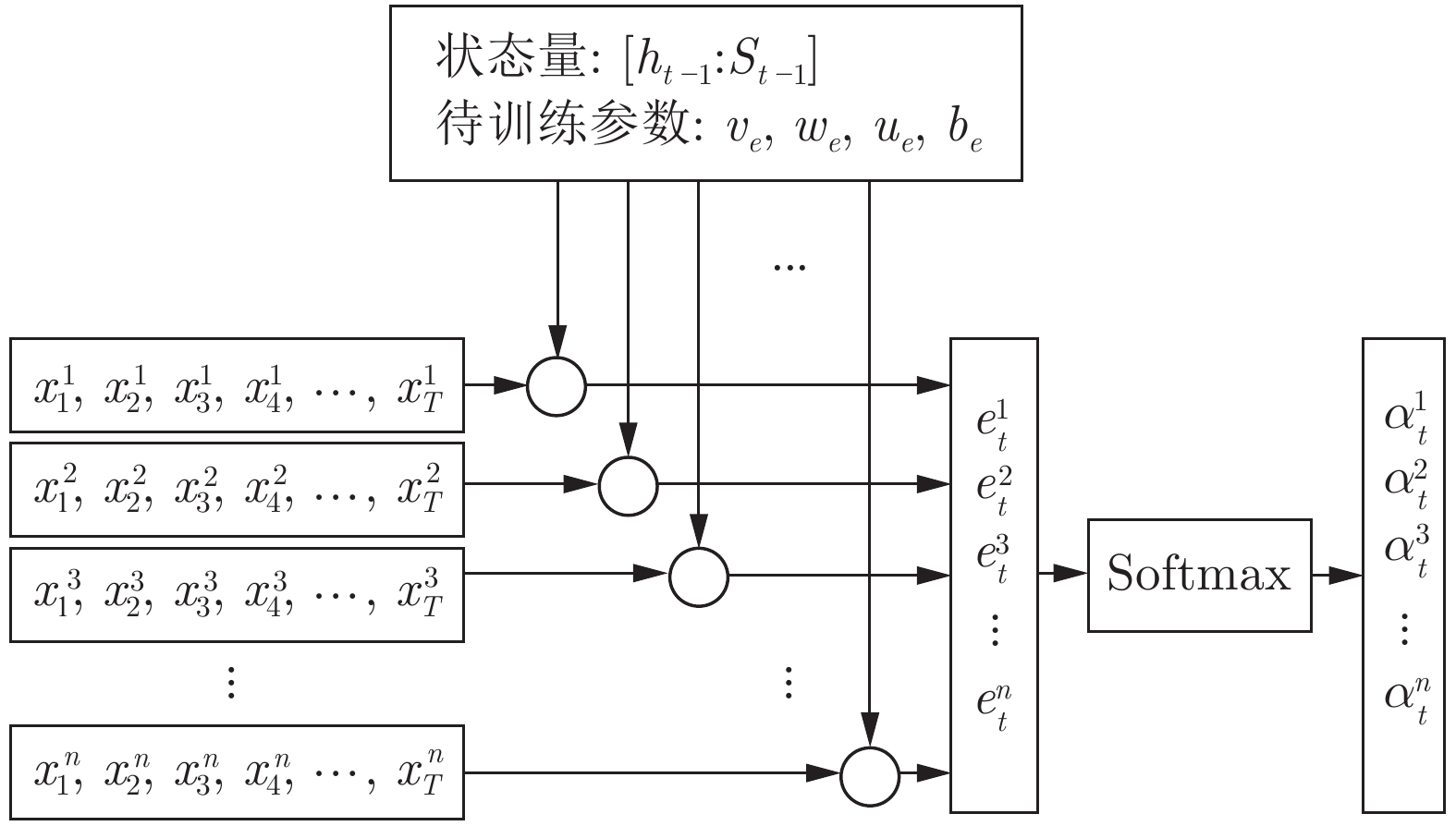
$t$ 时刻的数据不仅与其在$\left[ {t,t + T} \right]$ 时间段的数据具有相关性, 且与其余传感器数据在$t$ 时刻的数据存在空间相关性. 例如$t$ 时刻的位移数据与其在$\left[ {t,t + T} \right]$ 时间段内的数据具有相互依赖性, 且与$t$ 时刻的速度和加速度数据具有一定的关系. 根据该特性, 本节从空间维度上出发, 通过引入编码器模块中LSTM单元对应输入的前一个时刻的隐藏态${{\boldsymbol{h}}_{t - 1}}$ 和细胞态${{\boldsymbol{s}}_{t - 1}},$ 构建局部注意力机制来捕捉传感器数据序列之间的空间相关性. 局部注意力机制的结构如图2所示.如图2所示, 其中
$e_t^k$ 和$\alpha _t^k$ 的计算式为$$e_t^k = {\boldsymbol{v}}_e^ {{\rm{T}}} {\rm{tanh}}\left( {{{\boldsymbol{w}}_e}\left[ {{{\boldsymbol{h}}_{t - 1}}:{{\boldsymbol{s}}_{t - 1}}} \right] + {{\boldsymbol{u}}_e}{x^k} + {{\boldsymbol{b}}_e}} \right)$$ (2) $$\alpha _t^k = \frac{{{\rm{exp}}\left( {e_t^k} \right)}}{{\displaystyle\mathop \sum \limits_{i = 1}^n {\rm{exp}}\left( {e_t^i} \right)}}$$ (3) 其中,
${{\boldsymbol{v}}_e} \in {{\bf{R}}^T},{{\boldsymbol{w}}_e} \in {{\bf{R}}^{T \times 2H}},{{\boldsymbol{u}}_e} \in {{\bf{R}}^{T \times T}},{{\boldsymbol{b}}_e} \in {{\bf{R}}^T}$ 都是待训练的参数, 其中$H$ 表示LSTM中的隐藏单元数,${{\boldsymbol{v}}_e},{{\boldsymbol{w}}_e},{{\boldsymbol{u}}_e}$ 表示对状态量和输入做线性变换,${{\boldsymbol{b}}_e}$ 表示载体对传感器数据状态造成的影响.$e_t^k$ 表示第$k$ 个输入特征在$t$ 时刻的特征权重, 其经过softmax函数归一化后成为$\alpha _t^k,$ 即所有传感器数据在同一时刻内的权重之和为1. 因此, 局部注意力机制构建出的新的输入为$${\boldsymbol{x}}_t^{e1} = {(\alpha _t^1x_t^1,\alpha _t^2x_t^2, \cdots ,\alpha _t^nx_t^n)^{\rm{T}}},\;\;t \in [0,T]$$ (4) 3.2 全局注意力研究
当对传感器的数据状态进行判断时, 不同时间段内的传感器数据对整体的数据状态贡献是不一样的. 例如当判断
$\left[ {t + {{3T} / 4},t + T} \right]$ 时间段内的数据是否正常时,$\left[ {t + {{2T} / 4},t + {{3T} / 4}} \right]$ 时间段内的数据对其贡献程度比较大, 而$\left[ {t,t + {T / 4}} \right]$ 之内的数据状态对其贡献相对较小, 即每个时间段内的数据对其余时间段内数据状态的贡献程不一样. 根据该特性, 本节从时间维度出发, 通过引入上一个时刻编码器模块中LSTM单元对应输入的的隐藏态${{\boldsymbol{h}}_{t - 1}}$ 和细胞态${{\boldsymbol{s}}_{t - 1}}$ 来为每一时刻的输入分配权重. 全局注意力机制的结构如图3所示.如图3所示, 其中
${{\boldsymbol{g}}_t}$ 和${{\boldsymbol{\beta}} _t}$ 的计算式为$${{\boldsymbol{g}}_t} = {{\boldsymbol{v}}_g}{\rm{tanh}}\left( {{{\boldsymbol{w}}_g}\left[ {{{\boldsymbol{h}}_{t - 1}}:{{\boldsymbol{s}}_{t - 1}}} \right] + {{\boldsymbol{u}}_g}\left[ {{{\boldsymbol{x}}_t}:{{\boldsymbol{b}}_g}} \right]} \right)$$ (5) $${{\boldsymbol{\beta}} _t} = \frac{{{\rm{exp}}\left( {{{\boldsymbol{g}}_t}} \right)}}{{\mathop \sum \limits_{j = 1}^T {\rm{exp}}\left( {{{\boldsymbol{g}}_t}} \right)}}$$ (6) 其中,
${{\boldsymbol{v}}_g} \in {{\bf{R}}^n},{{\boldsymbol{w}}_g} \in {{\bf{R}}^{n \times 2H}},{{\boldsymbol{u}}_g} \in {{\bf{R}}^{1 + T}},{{\boldsymbol{b}}_g} \in {{\bf{R}}^{n \times T}}$ 都是待训练的参数, 其中${{\boldsymbol{v}}_g},{{\boldsymbol{w}}_g},{{\boldsymbol{u}}_g}$ 表示对状态量和输入做线性变换,${{\boldsymbol{b}}_g}$ 表示每类传感器数据的误差特性对数据状态的影响.${{\boldsymbol{g}}_t}$ 表示$t$ 时刻输入数据的特征权重, 即${{\boldsymbol{x}}_t}$ 的特征权重, 其经过softmax函数归一化后成为$\beta _t^k,$ 即所有传感器数据在$T$ 时刻内的权重之和为1. 因此, 全局注意力机制构建出的输入为$${{\boldsymbol{x}}^{e2}} = ({{\boldsymbol{\beta}} _1}{{\boldsymbol{x}}_1},{{\boldsymbol{\beta}} _2}{{\boldsymbol{x}}_2}, \cdots ,{{\boldsymbol{\beta}} _T}{{\boldsymbol{x}}_T})$$ (7) 对于编码器模块, 本文将局部注意力机制和全局注意力机制构建出的输入进行维度拼接后做为其新的输入, 即
$${\tilde {\boldsymbol{x}}_t} = [{{\boldsymbol{x}}^{e1}}:{{\boldsymbol{x}}^{e2}}],\;\;{\tilde {\boldsymbol{x}}_t} \in {{\bf{R}}^{n \times 2T}}$$ (8) 3.3 时间注意力机制
为了判断传感器数据在
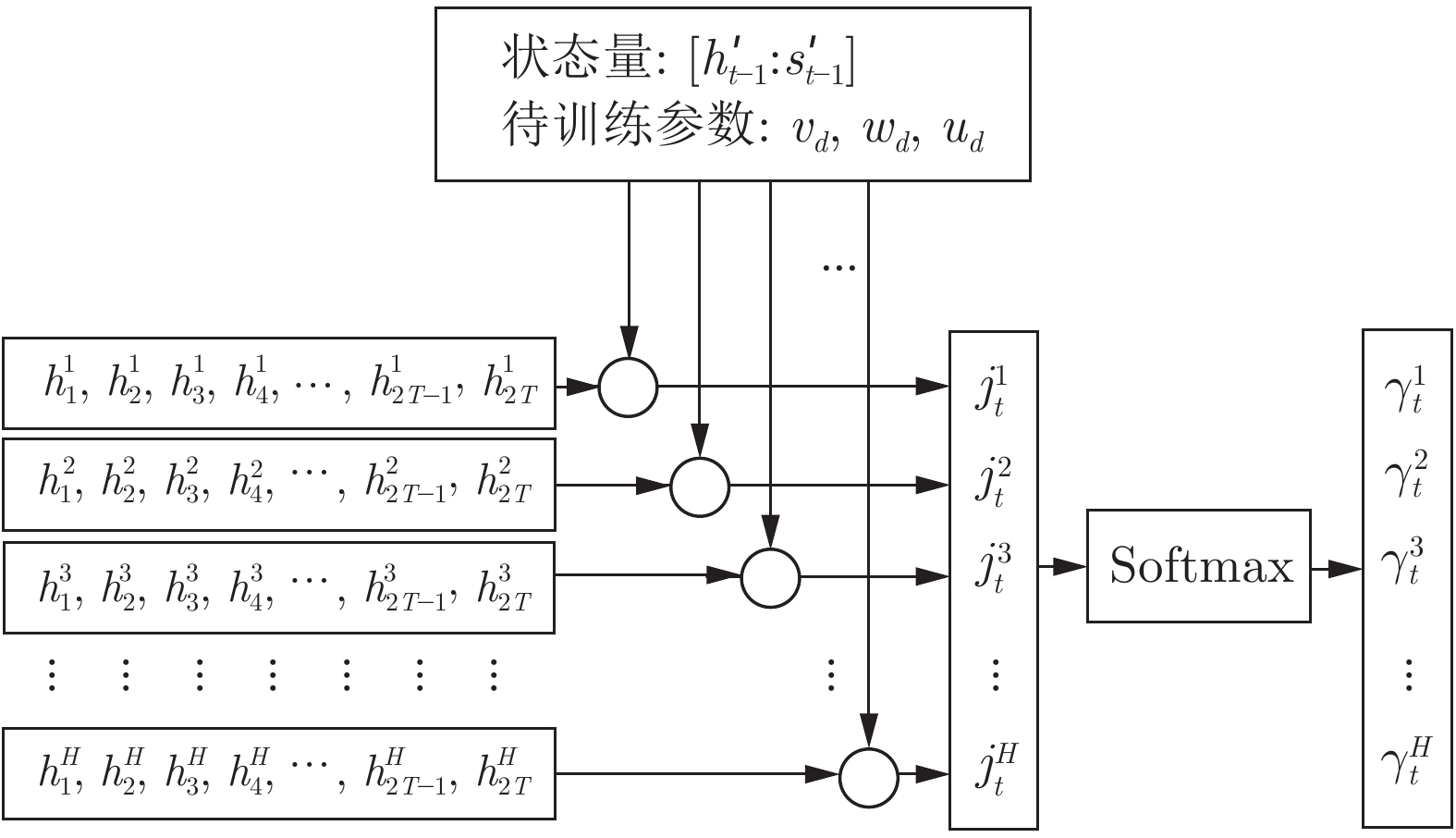
$T$ 时间段内的数据状态, 本文采用解码器模块解码来自编码器模块的编码信息. 由于编码器−解码器模型的性能会随着输入数据的长度而急剧衰减, 因此需要在解码器模型前引入时间注意力机制[16], 使其可以动态地选择编码器模块的相关输出序列并赋予不同的权重, 从而对其进行准确的解码. 本文的时间注意力机制如图4所示.如图4所示,
$j_t^i$ 和$\gamma _t^i$ 的计算式为$$j_t^i = {{\boldsymbol{v}}_d}{\rm{tanh}}\left( {{{\boldsymbol{w}}_d}\left[ {{\boldsymbol{h}}_{t - 1}':{\boldsymbol{s}}_{t - 1}'} \right] + {{\boldsymbol{u}}_d}{{\boldsymbol{h}}_t}} \right)\;\;\;\;$$ (9) $$\gamma _t^i = \frac{{{\rm{exp}}\left( {j_t^i} \right)}}{{\displaystyle\mathop \sum \limits_{j = 1}^H {\rm{exp}}\left( {j_t^j} \right)}}\qquad\qquad\qquad\qquad\;$$ (10) 其中,
${{\boldsymbol{v}}_d} \in {{\bf{R}}^H},{{\boldsymbol{w}}_d} \in {{\bf{R}}^{H \times 2H}},{{\boldsymbol{u}}_d} \in {{\bf{R}}^{H \times 2T}}$ 都是待训练的参数,${{\boldsymbol{h}}'_{t - 1}}$ 和${{\boldsymbol{s}}'_{t - 1}}$ 是解码器模块的$t - 1$ 时刻的隐藏态和细胞态,${{\boldsymbol{h}}_t} = (h_t^1,h_t^2, \cdots ,h_t^H)$ 是编码器模块在$t$ 时刻的输出,$\gamma _t^i$ 为$t$ 时刻第$i$ 个隐藏态$h_t^i$ 其对应的权重.解码器模型的输入为
$${\boldsymbol{x}}_t^d = (\gamma _t^1h_t^1,\gamma _t^2h_t^2, \cdots ,\gamma _t^{2H}h_t^{2H})$$ (11) 当采用解码器模型进行解码后, 将其输出传送给多层感知机, 对其进行非线性变化, 再采用softmax函数进行分类, 根据softmax输出则可以判断出传感器的数据状态.
4. 实验设计
4.1 实验数据
在导航系统中, 无论载体是飞机、汽车或者轮船, 其传感器数据都具有空间相关性和时间相关性, 只是载体运动规律不同, 其故障诊断的方法几乎都是一样的. 因此, 为了验证本文设计的基于多阶段注意力机制的故障诊断算法, 实验数据采用对MIT的开源车载数据[17]进行预处理之后的数据, 即对其开源车载数据注入故障. 该开源数据由一辆装配多种导航传感器的汽车在城市进行采集的, 并且已经进行了传感器的数据对准. 本文选取其中四个传感器的数据, 即陀螺仪、加速度计、GPS接收机和相机, 其对应的导航量为三轴角速率、三轴加速度、经度、纬度、高度、速度和双轴光流速度, 共12类传感器数据, 且每类传感器的数据个数为221280.
当传感器发生故障时, 一般是由于其温度、工作环境和元器件老化等多种原因造成的, 且该故障对传感器数据造成的影响很难用具体的数学模型来描述. 与工业系统相似, 许多研究学者将其故障模型抽象和理想化为阶跃响应、斜坡响应和加速度响应等数学模型. 因此, 对于本文研究的3种传感器故障, 即间歇型故障、渐变型故障和阶跃型故障, 采用理想化的数学模型, 如式(12)~(14)所示.
$$ y = \left\{ {\begin{aligned} &{k_1},&{t_1} < t < {t_2}\quad\;\,\\ &0,& t \le {t_1}{\text{或}}\;t \ge {t_2} \end{aligned}} \right. $$ (12) $$ y = \left\{ {\begin{aligned} &{k_2}t + b,& t > {t_3}\\ &0,&t \le {t_3} \end{aligned}} \right. $$ (13) $$ y = \left\{ {\begin{aligned} &{k_3},&t > {t_3}\\ &0,& t \le {t_3} \end{aligned}} \right. $$ (14) 考虑到各种故障类型的特性, 模型中参数的取值如下: 其中
$0 < {k_1} < {k_2} < T,\;0 < {k_3} < T,\;{k_1}$ 和${k_3}$ 取每类传感器数据在一个时间段$T$ 内的均值的0.1倍,${k_2}$ 取0.1,${t_1}$ 取$T/4,{t_2}$ 取$T/2,{t_3}$ 取$3T/4$ .为了模拟故障的传感器数据, 一方面需要对正常的传感器进行数据预处理; 另一方面需要列出所有可能的传感器故障组合. 首先, 从同一时间段内传感器故障数量的角度上将传感器的故障类型分为两大类, 即单故障和多故障. 单故障是指同一时间段内只有一个传感器数据发生故障, 多故障是指同一时间段内有多个传感器数据发生故障.
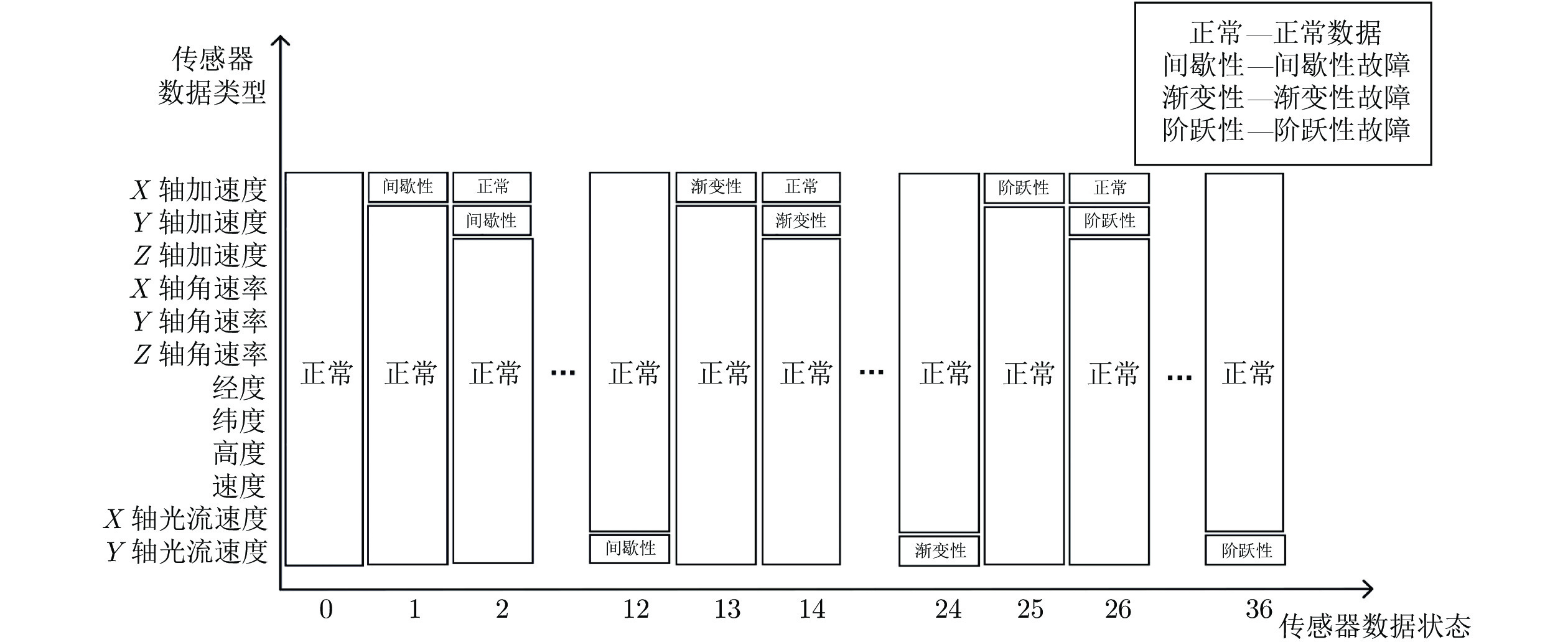
对于单故障类型的数据, 对每类传感器数据在不同时刻分别添加这3种故障, 即在一个时间段内, 只有一个传感器发生故障, 且为3种故障中的一种, 则预处理的传感器数据如图5所示.
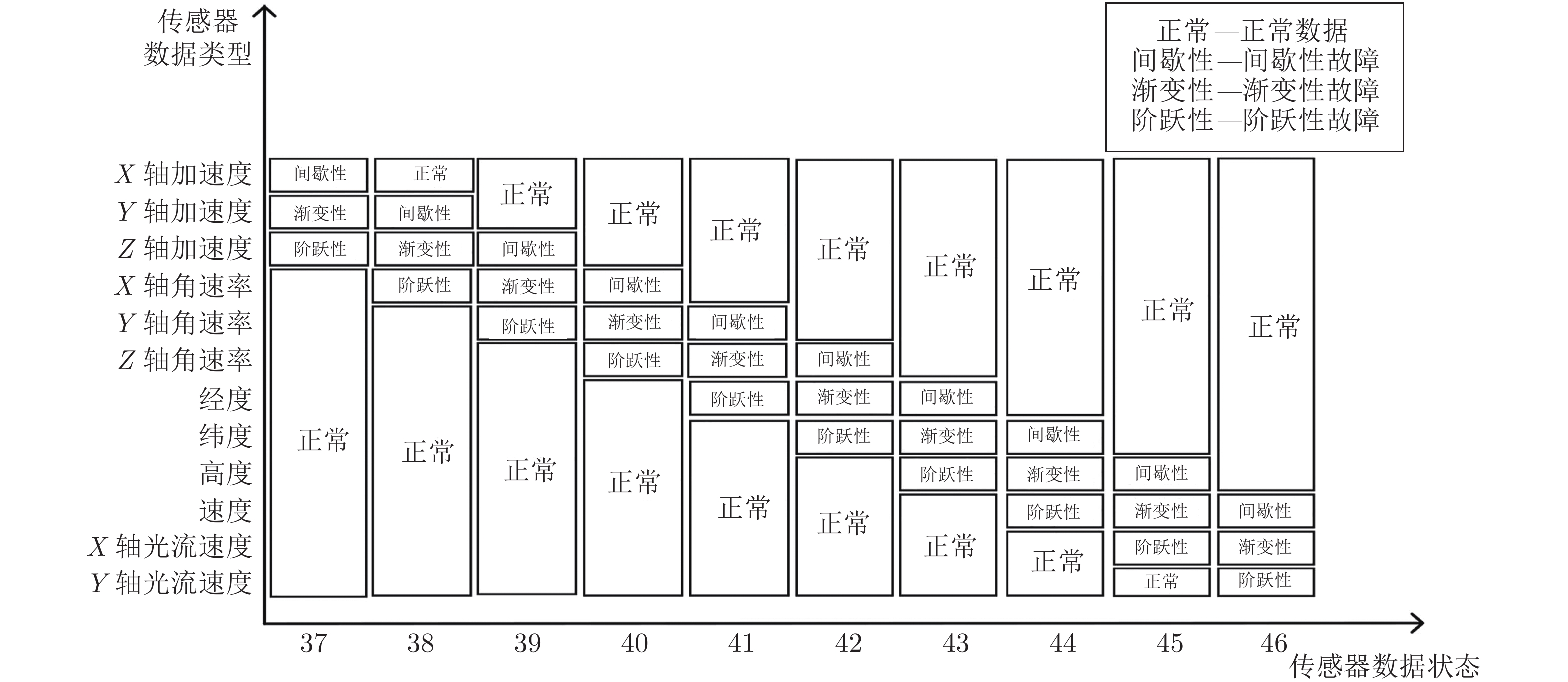
对于多故障数据, 由于传感器的故障类型有3种, 传感器数据有12种, 若使多个传感器发生不同类型的故障, 对其进行一一列举, 则整体传感器的数据状态会达到上百种, 会对训练网络带来一定的难度, 主要体现在实验平台的计算力上. 因此, 为了避免过多的传感器数据状态对训练网络带来的困难, 本文设多故障数据中传感器的故障数量为3, 其故障类型为间歇性、渐变性和阶跃性故障, 则多故障数据如图6所示.
如图5和图6所示, 输入
${\boldsymbol{x}} = {({{\boldsymbol{x}}^1},{{\boldsymbol{x}}^2}, \cdots ,{{\boldsymbol{x}}^n})^{\rm{T}}} =$ $({{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2}, \cdots ,{{\boldsymbol{x}}_T}) \in {{\bf{R}}^{n \times T}}$ 共有47种数据状态, 即46种故障状态和1种正常状态. 本文根据时间窗口$T$ 的大小, 将预处理的数据集按照8 : 1 : 1分为训练集、验证集和测试集, 每个数据集中每种状态的数据个数应基本相等, 其中训练集和验证集用来训练和验证模型, 测试集用来评估最终的模型性能.4.2 参数确定
本文中有多个参数需要确定. 对于数据集的时间窗口
$T$ , 设其区间设置为$T=$ {64, 96, 128, 144, 168, 196}; 对于编码器和解码器模块中的LSTM单元, 设其数目相同且将其范围设置为$H=$ {64, 96, 128, 192, 256}; 对于多层感知机, 设其每层隐藏单元数相等且设范围为$h=$ {3, 5, 7, 9}. 此外, 采用多层LSTM单元来增强模型的性能, 设其层数为$q.$ 最后, 经过网格搜索调参, 本文选取$T=144,\;H= $ $ 128,\; h=7,\; q=2$ .对模型进行训练时, 本文采用Adam优化器, 初始学习率为0.001, 每训练1 200步学习率减小为原来的0.8, Dropout取0.7, 批大小选择128, 训练20个Epochs, 采用交叉熵作为损失函数.
4.3 实验对比
此处将本文设计出来的多阶段注意力机制故障诊断算法称为FDRNN (Fault diagnosis recurrent neural network). 为了验证多阶段注意力机制对故障识别准确率的提升, 本文对FDRNN的子模型进行如下定义:
FDRNN-N1: 表示无局部注意力机制的网络;
FDRNN-N2: 表示无全局注意力机制的网络;
FDRNN-N3: 表示无时间注意力机制的网络.
对FDRNN及三个子模型、深度置信网络(Deep belief network, DBN)[7]和深度卷积神经网络(Deep convolutional neural network, DCNN)[8]进行对比实验, 结果如表1所示.
表 1 不同模型的实验对比Table 1 Comparison of experimental results of different models方法 准确率 (%) 召回率 (%) FDRNN 97.5 96.6 FDRNN-N1 83.4 81.5 FDRNN-N2 81.2 79.4 FDRNN-N3 74.3 72.1 DBN 80.5 78.9 DCNN 84.7 83.6 如表1所示, FDRNN的准确率可以达到97.5%, 召回率可以达到96.6%. 当没有局部注意力机制时, 其准确率和召回率会出现下降, 其主要原因是未将同一时刻不同传感器数据之间的空间相关性结合起来, 仅仅依靠单个传感器的数据对其数据状态做出判断, 因此准确率比较低. 当没有全局注意力机制时, 其准确率和召回率也会降低, 其原因在进行数据的状态判断时未考虑数据在时间维度上的前后相关性. 而当没有时间注意力时, 其准确率和召回率也会出现较大程度的下降, 关键原因是随着时间步的增长, 编码器的特征向量的语义信息会降低且解码器无法动态地从编码器模块中提取有用信息, 从而会降低模型的性能. 对于DBN而言, 其采用DBN网络对传感器数据进行在线估计, 根据估计值与真实值之间的残差来判断是否故障, 其结果很大程度上受残差阈值的影响, 且对多传感器故障的在线估计比较差, 因此仅有80.5%的准确率和78.9%的召回率. 对于DCNN而言, 其准确率可达84.7%, 召回率可以达到83.6%, 其原因是卷积网络中的卷积层和池化层一定程度上可以捕捉到多传感器数据之间的空间相关性和时间相关性, 但是其捕捉是基于随机搜索, 缺乏指导性, 所以其故障识别率相对于有多重注意力机制的编码器−解码器模型较低. 因此, 针对多传感器故障诊断任务, FDRNN可以准确地识别出故障传感器数据和故障类型.
本文构建出的FDRNN通过引入多阶段注意力机制将多个传感器数据在空间维度和时间维度之间的相互依赖性联系起来, 采用编码器−解码器结构对多传感器数据进行编码和解码, 再采用多层感知机进行分类. 该结构不仅可以准确识别出故障传感器, 并且可以识别出故障类型.
5. 结束语
本文提出的基于多阶段注意力机制的编码器−解码器模型在空间维度和时间维度上采用编码器来提取多传感器数据之间的空间相关性和时间相关性, 采用带有时间注意力机制的解码器来解码来自编码器的输出, 并采用多层感知机来判断时间窗口内数据的状态信息. 该方法通过多阶段注意力机制来捕捉多类传感器数据之间的关系, 采用多个传感器数据来辅助判断目标传感器, 形成多传感器之间的故障互检测, 不仅可以准确地检测出故障的传感器数据, 并且可以识别出其故障类型. 对比实验证明, 每阶段注意力机制都对判断数据的状态信息都具有非常重要的作用. 因此, 针对本文的多传感器故障诊断任务, FDRNN可以准确地进行故障检测.
-
-
[1] Tsitsiklis J N. Problems in decentralized decision making and computation [Ph. D. dissertation], MIT, Cambridge, MA, 1984 [2] Tsitsiklis J N, Bertsekas D P, Athans M. Distributed asynchronous deterministic and stochastic gradient optimization algorithms. IEEE Transactions on Automatic Control, 1986, 31(9): 803--812 doi: 10.1109/TAC.1986.1104412 [3] 洪奕光, 张艳琼. 分布式优化: 算法设计和收敛性分析. 控制理论与应用, 2014, 31: 850--857 doi: 10.7641/CTA.2014.40012Hong Yi-Guang, Zhang Yan-Qiong. Distributed optimization: algorithm design and convergence analysis. Control Theory & Applications, 2014, 31: 850--857(in Chinese) doi: 10.7641/CTA.2014.40012 [4] 衣鹏, 洪奕光. 分布式合作优化及其应用. 中国科学: 数学, 2016, 46(10): 1547--1564Yi Peng, and Hong Yi-Guang. Distributed cooperative optimization and its applications. SCIENTIA SINICA Mathematica, 2016, 46(10): 1547--1564(in Chinese) [5] 谢佩, 游科友, 洪奕光, 谢立华. 网络化分布式凸优化算法研究进展. 控制理论与应用, 2018, 35(7): 918--927 doi: 10.7641/CTA.2018.80205Xie Pei, You Ke-You, Hong Yi-Guang, Xie Li-Hua. A survey of distributed convex optimization algorithms over networks. Control Theory & Application, 2018, 35(7): 918--927(in Chinese) doi: 10.7641/CTA.2018.80205 [6] Nedić A, Olshevsky A, Rabbat M G. Network topology and communication-computation tradeoffs in decentralized optimization. Proceedings of the IEEE, 2018, 106(5): 953--976 doi: 10.1109/JPROC.2018.2817461 [7] 王龙, 卢开红, 关永强. 分布式优化的多智能体方法. 控制理论与应用, 2019, 36(11): 1820--1883 doi: 10.7641/CTA.2019.90502Wang Long, Lu Kai-Hong, and Guan Yong-Qiang. Distributed optimization via multi-agent systems. Control Theory & Applications, 2019, 36(11): 1820--1883(in Chinese) doi: 10.7641/CTA.2019.90502 [8] Yang T, Yi X L, Wu J F, Yuan Y, Wu D, Meng Z Y, et al A survey of distributed optimization. Annual Reviews in Control, 2019, 47: 278--305 doi: 10.1016/j.arcontrol.2019.05.006 [9] Khan U A, Bajwa W U, Nedić A, Rabbat M G, Sayed A H. Optimization for Data-Driven Learning and Control. Proceedings of the IEEE, 2020, 108(11): 1863--1868 doi: 10.1109/JPROC.2020.3031225 [10] 杨涛, 柴天佑. 分布式协同优化的研究现状与展望. 中国科学: 技术科学, 2020, 50(11): 1414--1425 doi: 10.1360/SST-2020-0040Yang Tao, Chai Tian-You. Research status and prospects of distributed collaborative optimization. SCIENTIA SINICA Technologica, 2020, 50(11): 1414--1425(in Chinese) doi: 10.1360/SST-2020-0040 [11] Johansson B, Keviczky T, Johansson M, Johansson K H. Subgradient methods and consensus algorithms for solving convex optimization problems. In: Proceedings of the IEEE Conference on Decision and Control, Cancun, Mexico: IEEE, 2008. 4185−4190 [12] Nedić A, Ozdaglar A. Distributed subgradient methods for multi-agent optimization. IEEE Transactions on Automatic Control, 2009, 54(1): 48--61 doi: 10.1109/TAC.2008.2009515 [13] Zhu M, Martínez S. On distributed convex optimization under inequality and equality constraints. IEEE Transactions on Automatic Control, 2012, 57(1): 151--164 doi: 10.1109/TAC.2011.2167817 [14] Nedić A, Olshevsky A. Distributed optimization over time-varying directed graphs. IEEE Transactions on Automatic Control, 2015, 60(3): 601--615 doi: 10.1109/TAC.2014.2364096 [15] Yang T, Lu J, Wu D, Wu J, Shi G, Meng Z, Johansson K H. A distributed algorithm for economic dispatch over time-varying directed networks with delays. IEEE Transactions on Industrial Electronics, 2017, 64(6): 5095--5106 doi: 10.1109/TIE.2016.2617832 [16] Matei I, Baras J S. Performance evaluation of the consensus-based distributed subgradient method under random communication topologies. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(4): 754--771 doi: 10.1109/JSTSP.2011.2120593 [17] Yuan K, Ling Q, Yin W. On the convergence of decentralized gradient descent. SIAM Journal on Optimization, 2015, 26(3): 1835--1854 [18] Shi W, Ling Q, Wu G, Yin W. EXTRA: An exact first-order algorithm for decentralized consensus optimization. SIAM Journal on Optimization, 2015, 25(2): 944--966 doi: 10.1137/14096668X [19] Yao L, Yuan Y, Sundaram S, Yang T. Distributed finite-time optimization. In: Proceedings of the 14th International Conference on Control and Automation. Anchorage, AK, USA: IEEE, 2018. 147−154 [20] Qu G, Li N. Harnessing smoothness to accelerate distributed optimization. IEEE Transactions on Control of Network Systems, 2018, 5(3): 1245--1260 doi: 10.1109/TCNS.2017.2698261 [21] Xu J, Zhu S, Soh Y C, Xie L. Augmented distributed gradient methods for multi-agent optimization under uncoordinated constant stepsizes. In: Proceedings of the 54th IEEE Conference on Decision and Control. Osaka, Japan: IEEE, 2015. 2055−2060 [22] Yang S, Tan S, Xu J X. Consensus based approach for economic dispatch problem in a smart grid. IEEE Transactions on Power Systems, 2013, 28(4): 4416--4426 doi: 10.1109/TPWRS.2013.2271640 [23] Du W, Yao L, Wu D, Li X, Liu G, Yang T. Accelerated distributed energy management for microgrids. In: Proceedings of the 2018 IEEE Power & Energy Society General Meeting. Portland, OR, USA: IEEE, 2018. 1−5 [24] Pu S, Shi W, Xu J, Nedić A. A push-pull gradient method for distributed optimization in networks. In: Proceedings of the 57th IEEE Conference on Decision and Control. Miami, FL, USA: IEEE, 2018. 3385−3390 [25] Xin R, Khan U A. A linear algorithm for optimization over directed graphs with geometric convergence. IEEE Control Systems Letters, 2018, 2(3): 325--330 [26] Zhu M, Martínez S. Discrete-time dynamic average consensus. Automatica, 2010, 46(2): 322--329 doi: 10.1016/j.automatica.2009.10.021 [27] Wang J, Elia N. Control approach to distributed optimization. In: Proceedings of the 48th Annual Allerton Conference on Communication, Control, and Computing. Allerton, Illinois, USA: IEEE, 2010. 557−561 [28] Gharesifard B, Cortés J. Distributed continuous-time convex optimization on weight-balanced digraphs. IEEE Transactions on Automatic Control, 2014, 59(3): 781--786 doi: 10.1109/TAC.2013.2278132 [29] Kia S S, Cortés J, Martínez S. Distributed convex optimization via continuous-time coordination algorithms with discrete-time communication. Automatica, 2015, 55: 254--264 doi: 10.1016/j.automatica.2015.03.001 [30] Lu J, Tang C Y. Zero-gradient-sum algorithms for distributed convex optimization: The continuous-time case. IEEE Transactions on Automatic Control, 2012, 57(9): 2348--2354 doi: 10.1109/TAC.2012.2184199 [31] Varagnolo D, Zanella F, Cenedese A, Pillonetto G, Schenato L. Newton-Raphson consensus for distributed convex optimization. IEEE Transactions on Automatic Control, 2016, 61(4): 994--1009 doi: 10.1109/TAC.2015.2449811 [32] Wei E, Ozdaglar A, Jadbabaie A. A distributed Newton method for network utility maximization-I: Algorithm. IEEE Transactions on Automatic Control, 2013, 58(9): 2162--2175 doi: 10.1109/TAC.2013.2253218 [33] Aström K J, Bernhardsson B M. Comparison of Riemann and Lebesgue sampling for first order stochastic systems. In: Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA: IEEE, 2002. 2011−2016 [34] Tabuada P. Event-triggered real-time scheduling of stabilizing control tasks. IEEE Transactions on Automatic Control, 2007, 52(9): 1680--1685 doi: 10.1109/TAC.2007.904277 [35] Girard A. Dynamic triggering mechanisms for event-triggered control. IEEE Transactions on Automatic Control, 2015, 60(7): 1992--1997 doi: 10.1109/TAC.2014.2366855 [36] Dimarogonas D V, Frazzoli E, Johansson K H. Distributed event-triggered control for multi-agent systems. IEEE Transactions on Automatic Control, 2012, 57(5): 1291--1297 doi: 10.1109/TAC.2011.2174666 [37] Seyboth G S, Dimarogonas D V, Johansson K H. Event-based broadcasting for multi-agent average consensus. Automatica, 2013, 49(1): 245--252 doi: 10.1016/j.automatica.2012.08.042 [38] Meng X, Xie L, Soh Y C, Nowzari C, Pappas G J. Periodic event-triggered average consensus over directed graphs. In: Proceedings of the 54th IEEE Transactions on Decision and Control. Osaka, Japan: IEEE, 2015. 4151−4156 [39] Meng X, Xie L, Soh Y C. Asynchronous periodic event-triggered consensus for multi-agent systems. Automatica, 2017, 84: 214--220 doi: 10.1016/j.automatica.2017.07.008 [40] Yi X. Resource-constrained multi-agent control systems: Dynamic event-triggering, input saturation, and connectivity preservation. [Master thesis], Royal Institute of Technology, Sweden, 2017 [41] Nowzari C, Cortés J, Pappas G. Event-triggered control for multi-agent average consensus. Cooperative Control of Multi-Agent Systems. John Wiley & Sons, Ltd, 2018, 177−208 [42] Yi X, Yang T, Wu J, Johansson K H. Distributed event-triggered control for global consensus of multi-agent systems with input saturation. Automatica, 2019, 100: 1--9 doi: 10.1016/j.automatica.2018.10.032 [43] Liu S, Xie L, Quevedo D E. Event-triggered quantized communication-based distributed convex optimization. IEEE Transactions on Control of Network Systems, 2018, 5(1): 167--178 doi: 10.1109/TCNS.2016.2585305 [44] Chen W, Ren W. Event-triggered zero-gradient-sum distributed consensus optimization over directed networks. Automatica, 2016, 65: 90--97 doi: 10.1016/j.automatica.2015.11.015 [45] Du W, Yi X, Jemin G, Johansson K H, Yang T. Distributed optimization with dynamic event-triggered mechanisms. In: Proceedings of the 57th IEEE Conference on Decision and Control, Miami, FL, USA: IEEE, 2018. 969−974 [46] Yi X, Yao L, Yang T, George J, Johansson K H. Distributed optimization for second-order multi-agent systems with dynamic event-triggered communication. In: Proceedings of the 57th IEEE Conference on Decision and Control, Miami, FL, USA: IEEE, 2018. 3397−3402 [47] Wang D, Gupta V, Wang W. An event-triggered protocol for distributed optimal coordination of double-integrator multi-agent systems. Neurocomputing, 2018, 319(30): 34--41 [48] Liu C, Li H, Shi Y, Xu D. Event-triggered broadcasting for distributed smooth optimization. In: Proceedings of the 58th IEEE Conference on Decision and Control, Nice, France: IEEE, 2019. 716−721 [49] Liu C, Li H, Shi Y, Xu D. Distributed event-triggered gradient method for constrained convex minimization. IEEE Transactions on Automatic Control, 2020, 65(2): 778--785 doi: 10.1109/TAC.2019.2916985 [50] Li M, Su L, Liu T. Distributed optimization with event-triggered communication via input feedforward passivity. IEEE Control Systems Letters, 2020, 5(1): 283--288 [51] Johansson K H, Egerstedt M, Lygeros J, Sastry S. On the regularization of Zeno hybrid automata. Systems & Control Letters, 1999, 38(3): 141--150 [52] Godsi C, Royle G F, Algebraic Graph Theory, ser. Graduate Texts in Mathematics. New York: Springer-Verlag, 2001, 207 [53] Khalil H K, Nonlinear Systems, 3rd ed. Prentice-Hall, New Jersey, 2002 期刊类型引用(17)
1. 赵中原,高旺,蒋璐瑶,葛泉波. 基于椭圆曲线ELGamal的隐私保护分布式优化算法. 自动化学报. 2025(01): 210-220 .  本站查看
本站查看2. 武文强,王庆领. 基于比例积分调节的严格反馈多智能体系统最优一致性. 自动化学报. 2025(03): 577-589 .  本站查看
本站查看3. 刘奕葶,马铭莙,付俊. 基于有向图的分布式连续时间非光滑耦合约束凸优化分析. 自动化学报. 2024(01): 66-75 .  本站查看
本站查看4. 张捷,姚瑶,王健安,李志强. 固定和切换拓扑下多智能体系统二分容错状态一致性研究. 控制工程. 2024(03): 439-449 .  百度学术
百度学术5. 杨志强,贾红云,韦梦立,季秋桐,赵中原. 最小事件间隔时间可设计的分布式事件触发优化算法. 南京信息工程大学学报. 2024(02): 179-185 .  百度学术
百度学术6. 时侠圣,孙长银,穆朝絮. 扰动线性多智能体系统的分布式资源分配算法. 中国科学:信息科学. 2024(04): 911-926 .  百度学术
百度学术7. 宁君,彭周华,李铁山,陈俊龙. 带有输入量化的分布式多无人船舶自适应模糊编队控制. 控制与决策. 2024(08): 2588-2596 .  百度学术
百度学术8. 时侠圣,孙佳月,徐磊,杨涛. 二阶智能体的分布式非光滑资源分配算法. 控制与决策. 2023(05): 1336-1344 .  百度学术
百度学术9. 杨菲阳,于志永,蒋海军,黄达. 事件触发间歇通讯下多智能体系统的固定时间分布式优化. 控制与决策. 2023(05): 1412-1419 .  百度学术
百度学术10. 衣鹏,潘越,王文远,刘政钦,洪奕光. 基于博弈论的多车智能驾驶交互决策综述. 控制与决策. 2023(05): 1159-1175 .  百度学术
百度学术11. 杨涛,常怡然,张坤朋,徐磊. 基于预设时间收敛的分布式优化算法. 控制与决策. 2023(08): 2364-2374 .  百度学术
百度学术12. 刘腾飞,秦正雁,姜钟平. 分布式反馈优化研究现状与发展. 控制与决策. 2023(08): 2301-2312 .  百度学术
百度学术13. 时侠圣,林志赟,王雪松,董世建. 非平衡有向网络的完全分布式凸优化. 控制理论与应用. 2022(06): 1071-1078 .  百度学术
百度学术14. 崔丹丹,刘开恩,纪志坚,田昌源,崔秋燕. 周期事件触发的多智能体分布式凸优化. 控制工程. 2022(11): 2027-2033 .  百度学术
百度学术15. 孟 敏, ,李修贤 . Aug-PDG:带不等式约束凸优化算法的线性收敛性(英文). 控制理论与应用. 2022(10): 1969-1977 .  百度学术
百度学术16. 时侠圣,徐磊,杨涛. 基于自适应精确罚函数的分布式资源分配算法. 控制理论与应用. 2022(10): 1937-1945 .  百度学术
百度学术17. 李修贤,李莉,谢立华. 含生成森林有向图的零特征值及在编队控制中的应用(英文). 控制理论与应用. 2022(10): 1799-1806 .  百度学术
百度学术其他类型引用(16)
-





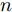
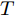
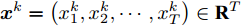
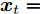
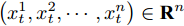
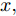
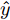
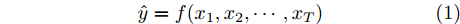
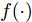

 下载:
下载:
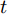
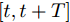
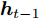
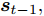
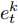
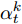
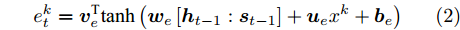
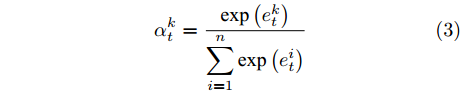
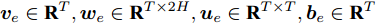
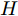
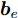
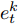
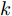
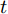
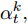
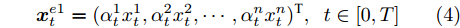
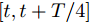
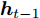
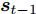

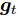
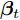
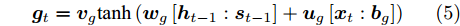
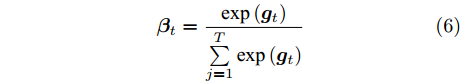
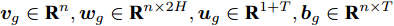
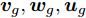
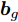
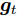
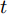
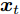
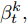
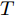
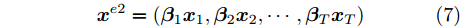
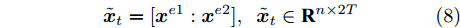
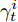
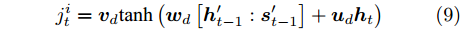
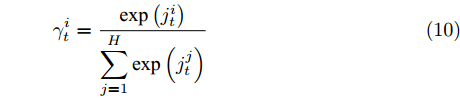
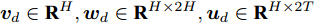
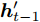
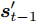

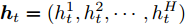
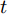
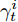

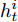
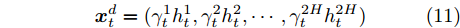
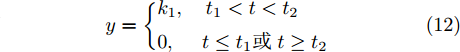
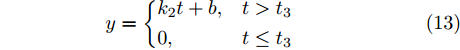
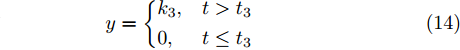
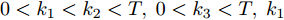
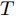
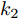
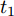
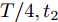
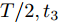
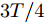
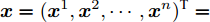
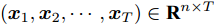
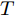
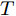
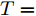
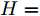
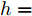
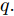
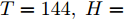
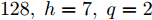


 下载:
下载: