Multiple Generalized Eigenvalue Decomposition Algorithm in Parallel Based on Weighted Matrix
-
摘要: 针对串行广义特征值分解算法实时性差的缺点, 提出基于加权矩阵的多维广义特征值分解算法. 与串行算法不同, 所提算法能够在一次迭代过程中并行地估计出多维广义特征向量. 平稳点分析表明: 当且仅当算法中状态矩阵等于所需的广义特征向量时, 算法达到收敛状态. 通过对比相邻时刻的状态矩阵模值证明了所提算法的自稳定特性. 所提算法参数选取简单, 实际实施较为容易. 数值仿真和实例应用进一步验证了算法的并行性、自稳定性和实用性.Abstract: In order to overcome the disadvantages of sequential algorithms, such as poor real time, a multiple generalized eigenvalue decomposition algorithm is proposed based on weighted matrix method. Unlike sequential algorithms, the proposed algorithm is able to estimate multiple generalized eigenvectors in parallel only through one iteration procedure. The stationary point analysis shows that the algorithm reaches convergence state if and only if the state matrix is equal to the desired generalized eigenvectors. The self-stabilization characteristics of the proposed algorithm is proved by comparing the state matrix module values of adjacent moments. The proposed algorithm parameters are simple to select and easy to implement in practice. Numerical simulation and example application further verify the parallelism, self-stability and practicality of the algorithm.
-
在深海勘探开发生产中, 海洋柔性立管作为连接海面作业平台与海床井口的关键构件[1].在风、浪、洋流等外部载荷作用下, 海洋立管会产生振动现象, 而长期的振动则是造成柔性立管疲劳破损的主因[2-4].因此, 开展先进的海洋柔性立管振动主动控制系统研究, 对延长立管使用寿命、提高生产效率和保证海洋油气生产安全具有重要的理论和实际意义.
从数学的观点看, 具有振动的海洋柔性立管系统可认为是典型的无限维分布参数系统[5-11].其动力学往往建模为耦合的偏微分–常微分方程, 这使得现有许多对传统刚性系统成熟的方法不能直接应用.对海洋柔性立管振动控制的研究主要包括模态控制和边界控制.模态控制是基于提取的有限维受控子系统进行控制设计, 而忽略掉的高频模态可能导致系统产生控制溢出效应.边界控制能克服上述方法的缺点, 且容易由系统机械能相关的Lyapunov函数得出, 因此边界控制与其他控制技术如PID控制、鲁棒控制、自适应控制、反步控制、输出反馈控制等相结合的方法广泛应用于柔性立管系统的振动控制领域[12-16].上述研究仅仅局限于柔性立管系统的振动控制, 而这些方法将不适用于具有输入非线性特性的柔性立管系统.
在实际的海洋油气生产环境中, 柔性立管系统除了受到风浪扰动和海洋洋流分布式扰动影响外, 其面临的情况可能会比之前研究的问题更加复杂.如系统固有的物理约束和执行器的约束将使得系统产生死区、饱和、磁滞、反向间隙等不光滑的非线性特性[17-20].而这些不光滑的非线性特性将会限制系统的瞬态性能, 更为甚者, 将会致使系统不稳定.因此, 需要将这些不光滑的非线性约束特性考虑在控制设计中.为了解决海洋柔性立管系统的输入非线性约束问题, 一些学者基于立管原始无限维模型探索了不同的边界控制方法[13, 21-24].文献[13]面向具有系统不确定性、输出约束和输入饱和的海洋立管系统, 基于反推技术研发了障碍边界控制策略以抑制振动、补偿系统不确定性以及处理系统的输入输出限制.文献[21]针对具有执行器输入饱和非线性约束和外部海洋扰动的海洋柔性立管系统, 在顶端构建边界控制器以稳定其在平衡位置的小邻域并利用辅助系统补偿执行器饱和的影响.文献[22]设计了鲁棒自适应控制器用以稳定具有参数不确定性和输入受限的海洋柔性立管系统.文献[23]采用光滑的双曲正切函数、Nussbaum函数和辅助系统设计边界控制器以抑制立管振动并限制控制输入在给定范围内, 该方法解决了文献[21−22]中应用符号函数限制控制输入所带来的震颤问题.文献[24]引入辅助函数和变量设计边界控制器来实现立管的振动减弱并消除混合的死区−饱和非线性约束影响.然而, 这些成果仅仅解决了柔性立管系统执行器输入饱和或输入饱和−死区非线性约束问题, 而对于具有输入反向间隙−饱和非线性约束的柔性立管系统, 上述方法将不能适用.
本文针对执行器非光滑反向间隙−饱和约束特性的深海柔性立管系统(如图 1所示), 首先将反向间隙−饱和约束转换成虚拟的输入饱和约束, 其后引入辅助系统并采用Lyapunov理论, 构建边界控制以抑制柔性立管的振动并消除饱和非线性约束的影响.随后, 证明了闭环系统在Lyapunov意义下的一致有界稳定性.最后, 通过数值仿真, 验证了本文所提出控制能处理非光滑反向间隙−饱和约束非线性影响, 也能有效抑制立管系统振动.
1. 问题描述和预备知识
注1.本文作如下简写: $ (\cdot)(x, t) = (\cdot) $, $ (\cdot)' = \dfrac{\partial(\cdot)}{\partial{x}} $, $ \dot{(\cdot)} $ = $ \dfrac{\partial(\cdot)}{\partial{t}} $.
1.1 立管动力学模型
深海柔性立管系统如图 1所示, 其中$ l $为立管的长度, $ y(z, t) $为立管在位置$ z $时刻$ t $的偏移量, $ f(z, t) $为海洋洋流分布式扰动, $ d(t) $为外部环境扰动, $ u(t) $为边界控制输入.
本研究所考虑立管系统动力学描述如下[1]:
$\begin{split} \rho\ddot{y}(z,&t)-\left\{T[z, y'(z,t)]+\right.\\ & \left.3\psi(z)y'^2(z,t)\right\}y''(z,t)-\\ & \ T'[z, y'(z,t), y''(z,t)]y'(z,t)+c\dot{y}(z,t)-\\ & \ \psi'(z)y'^3(z,t)+ EIy''''(z,t)-\\ & \ f(z,t) = 0,\ \ \ 0<z<l \end{split} \hspace{33pt} $
(1) $ \begin{align} y(0,t) = y'(0,t) = y''(l,t) = 0 \end{align} \hspace{78pt} $
(2) $ \begin{split} m\ddot{y}(l,t)+& T[l, y'(l,t)]y'(l,t)+\psi(l)y'^3(l,t)-u(t)+\\ & d_a\dot{y}(l,t) = EIy'''(l,t)+d(t) \end{split} \hspace{5pt}$
(3) 其中, $ \rho $, $ c $和$ EI $分别为立管的单位长度质量、阻尼系数和弯曲刚度, $ d_a $和$ m $为船的质量和阻尼系数, $ T[z, y'(z, t)] $为立管的时空变化张力, 表示为
$ \begin{align} T[z, y'(z,t)] = T_0(z)+\psi(z)y'^2(z,t) \end{align} $
(4) 其中, $ T_0(z) > 0 $为初始张力, $ \psi(z)\ge 0 $为非线性弹性模量.
执行器输入饱和非线性描述为[25]
$ \begin{align} \varphi(t) = sat(\varrho(t)) = \begin{cases} a , \qquad\quad\ \varrho(t)\ge a \\[2mm] \varrho(t) , \qquad -a < \varrho(t) < a \\[2mm] -a, \qquad\ \ \, \varrho(t)\ -a \end{cases} \end{align} $
(5) 其中, $ a > 0 $为饱和界限.
执行器输入反向间隙非线性描述为[24]
$\begin{array}{l} u(t) = D(\varphi (t)) = \\ \qquad\;\;\;\left\{ {\begin{aligned} &{\varphi (t) - b,\;\qquad \dot \varphi }{ > 0\;\text{且}\;u(t) = \varphi (t) - b}\\ &{\varphi (t) + b,\;\qquad \dot \varphi }{ < 0\;\text{且}\;u(t) = \varphi (t) + b}\\ &{u(t\_), \qquad\quad\;\; \text{其他}}&{} \end{aligned}} \right. \end{array}$
(6) 其中, $ b > 0 $为反向间隙参数.
由输入饱和与反向间隙的表达式(5)和式(6)可知, 系统的非线性特征是相当复杂的, 因此很难直接对其处理.根据文献[25], 可知输入饱和与反向间隙可转换并表示为一个虚拟的输入饱和.因此, 为解决虚拟的输入非线性问题, 我们引入$ D $的右逆$ D^+ $为
$ \begin{align} \varrho(t) = D^+(\tau(t)) = \left\{ \begin{aligned} & \tau(t)+b, \; \; \dot{\tau}(t)>0 \\ & \tau(t)-b, \; \; \dot{\tau}(t)<0 \\ & \varrho(t\_), \; \;\;\;\;\; \dot{\tau}(t) = 0 \end{aligned} \right. \end{align} $
(7) 根据上面的分析和文献[25], 我们可得混合的输入饱和−反向间隙非线性特性可描述为
$ \begin{split} u(t) = & D(sat(D^+(\tau(t)))) = \\ &\left\{ \begin{aligned} & \,a-b, \qquad\;\;\, \tau(t)\ge a-b \\ & \, \tau(t), \qquad\quad\; |\tau(t)|<a-b \\ & -a+b, \quad\;\;\tau(t)\le-a+b \end{aligned} \right. \end{split} $
(8) 由式(8)可知, 我们可将系统的输入饱和−反向间隙非线性视为一个输入饱和来处理.
1.2 预备知识
引理1[26].设$ \chi_1(z, t) $, $ \chi_2(z, t)\in {\bf{R}} $, $ \varphi > 0 $, 其中$ (z, t)\in$ $[0, l]\times[0, +\infty) $, 则
$ \begin{align} \chi_1(z,t)\chi_2(z,t)\le \frac{1}{\varphi}\chi^2_1(z,t)+\varphi\chi^2_2(z,t) \end{align} $
(9) 引理2[26].设$ \chi(z, t)\in {\bf{R}} $为定义在$ (z, t)\in[0, l]\times $ $[0, +\infty) $的函数, 且满足$ \chi(0, t) = 0, \forall t\in[0, +\infty) $, 则
$ \begin{align} \chi^2(z,t) \le l\int^l_0\chi^{{\prime}2}(z,t){\rm{d}}z \end{align} $
(10) 假设1.假定存在常数$ {F} $, $ {D}\in {\bf{R}}^+ $, 使得$\mid f(z, t)\mid \leq $ $ {F, } $ $ \forall{(z, t)}\in{[0, l]\times[0, +\infty), } $ $\mid d(t)\mid \leq {D, } $ $ \forall{t}\in[0, +\infty). $这个假设是合理的, 由于$ f(z, t) $和$ d(t) $是有限能量的, 因此是有界的[21-24].
假设2.假定存在正常数$ \underline{T}_0 $, $ \overline{T}_0 $, $ \underline{\psi}_0 $, $ \overline{\psi}_0 $, 使得$ \underline{T}_0\le T_0(z) \le \overline{T}_0 $, $ \underline{\psi}_0\le \psi(z)\leq \overline{\psi}_0 $.
假设3.对于新的输入饱和表达式(8), 假定存在一个正常数$ \varpi $使得$ |\triangle u|\le \varpi $, 其中, $ \triangle u = u(t)-$ $\tau(t) $.
2. 控制器设计
本节将引入辅助函数和辅助系统用于构建边界控制器以抑制立管振动并消除输入非线性影响.
2.1 边界控制器
首先, 设计辅助系统为
$ \begin{split}\! \dot{\nu}(t) =&\ \frac{1}{m}\left(-k_1\nu(t)-\triangle u+T[l, y'(l,t)]y'(l,t)+ \right. \\ & \left. \psi(l)y'^3(l,t)+d_a\dot{y}(l,t)-EIy'''(l, t)\right) \end{split} $
(11) 其中, $ \nu(t) $为辅助系统的状态变量, $ k_1 $为正常数.
为便于分析闭环立管系统的稳定性, 定义如下辅助变量
$\begin{split} \mu(t) =\;& \dot{y}(l,t)-k_2y'''(l, t)+y'(l,t)+\\ &k_3y'^3(l,t)+\nu(t) \end{split}$
(12) 其中, $ k_2, k_3 $为正常数.
对式(12)求导, 代入式(3)和式(11), 可得
$ \begin{aligned} \dot{\mu}(t) =\;& \frac{1}{m}(\tau(t)+d(t)-mk_2\dot{y}'''(l, t)+m\dot{y}'(l,t)+\\ & 3mk_3y'^2(l,t)\dot{y}'(l,t)-k_1\nu(t)) \end{aligned} $
(13) 根据上述分析, 提出控制律$ \tau(t) $为
$ \begin{aligned} \tau(t) = & -k_4\mu(t)+k_1\nu(t)+mk_2\dot{y}'''(l, t)-m\dot{y}'(l,t) -\\ & \ 3mk_3y'^2(l,t)\dot{y}'(l,t)-{\rm{sgn}}(\mu(t)){D} \end{aligned} $
(14) 其中, $ k_4 $为正常数.
注2.所设计的控制器(14)是由可获得的边界信号组成的, 其中$ y'''(l, t) $、$ y'(l, t) $和$ y(l, t) $分别可由剪切力传感器、倾角计和位移传感器获得.此外, 控制器中这些信号的一阶时间微分信号$ \dot{y}'''(l, t), $ $ \dot{y}'(l, t) $和$ \dot{y}(l, t) $分别可对已获得信号进行后向差分算法得到[21-24].
选取如下Lyapunov函数为
$ Y(t) = {{Y}_{e}}(t)+{{Y}_{f}}(t)+{{Y}_{g}}(t) $
(15) 其中,
$ \begin{align} {{Y}_{e}}(t) = \frac{\varsigma}{2}\rho\int_{0}^{l}{{{{\dot{y}}}^{2}}(z,t){\rm{d}}z} +\frac{\varsigma}{2}\int_{0}^{l}T_0(z){{{ {y}^{\prime2}\left( z,t\right) }}{\rm{d}}z}+\\ \frac{\varsigma}{2}\int_{0}^{l}\psi(z){{{ {y}^{\prime4}\left( z,t\right) }}{\rm{d}}z}+\frac{\varsigma}{2}EI\int_{0}^{l}y^{\prime\prime 2}(z,t){\rm{d}}z \end{align} $
(16) $ \begin{align} {{Y}_{g}}(t) = \frac{\varsigma m}{2}\nu^2(t)+\frac{\varsigma m}{2}\mu^2(t) \end{align} \hspace{78pt}$
(17) $ \begin{align} {{Y}_{f}}(t) = \lambda\rho\int_{0}^{l} z \phi(z){\dot{y} (z,t){y}'(z,t){\rm{d}}z} \end{align} $
(18) 其中, $ \varsigma, \lambda > 0 $.
引理3.选取的Lyapunov函数(16)是一个正定的函数:
$ \begin{split} 0\le\; & \delta_1[Y_e(t)+Y_f(t)]\le Y(t)\le \\ &\delta_2[Y_e(t)+Y_f(t)] \end{split} $
(19) 其中, $ \delta_1 > 0, \; \delta_2 > 1 $.
证明.根据引理1, 式(18)可放缩为
$ \begin{split} \mid Y_g(t)\mid\ \le\ & \frac{\lambda\rho \overline{\phi}l}{2}\int^l_0[\dot{y}^2(z,t)+\\ &\ y^{{\prime}2}(z,t)]{\rm{d}}z \le \delta_0{Y_e(t)} \end{split} $
(20) 其中
$ \begin{align} \delta_0 = \frac{\lambda \rho \overline{\phi}l}{\min\left({\varsigma}\rho, {\varsigma}\underline{T_0}\right)} \end{align} $
(21) 通过恰当地选取$ \varsigma $和$ \beta $得出
$ \begin{align} \delta_1 = 1-\delta_0>0, \;\delta_2 = 1+\beta_0>1 \end{align} $
(22) 式(22)表明$ 0 < \delta < 1 $, 应用式(21)可得
$ \begin{align} {\varsigma}>\frac{\lambda \rho \overline{\phi}l}{\min\left(\rho, \underline{T_0}\right)} \end{align} $
(23) 重排式(20), 有
$ \begin{align} -{\delta}Y_e(t)\le Y_g(t)\le {\delta}Y_e(t) \end{align} $
(24) 将式(22)代入式(24)得出
$ \begin{align} 0\le \delta_1 Y_e(t)\le Y_e(t)+Y_g(t)\leq \delta_2 Y_e(t) \end{align} $
(25) 结合式(15), 有
$ \begin{aligned} 0\le\;& \delta_1[Y_e(t)+Y_f(t)]\le Y(t)\leq\\ &\delta_2[Y_e(t)+Y_f(t)] \end{aligned} $
(26) 其中, $ \delta_1 > 0, \; \delta_2 > 1 $.
引理4.选取Lyapunov函数(16)的导数是有上界的:
$ \begin{align} \dot{Y}(t)\le -\delta Y(t)+\alpha \end{align} $
(27) 其中, $ \delta, \alpha > 0 $.
证明.对式(16)求导, 可得:
$ \begin{align} \dot{Y}(t) = \dot{Y}_e(t)+\dot{Y}_f(t)+\dot{Y}_g(t) \end{align} $
(28) 将式(16)求导, 代入式(1)并应用引理1, 可得
$ \begin{aligned} \dot{Y}_e(t)\leq \; &\frac{\varsigma T_0(l)}{2}\mu^2(t)-\frac{\varsigma T_0(l)}{2}\nu^2(t)-\frac{\varsigma T_0(l)}{2}\dot{y}^2(l,t)-\\& \frac{\varsigma T_0(l)k^2_2}{2}y'''^2(l,t)-\frac{\varsigma T_0(l)}{2}y'^2(l,t)-\\ & \frac{\varsigma T_0(l)k^2_3}{2}y'^6(l,t)+{\varsigma T_0(l)}{k_2}\nu(t){y}'''(l,t)-\\ & ({\varsigma EI}-{\varsigma T_0(l)}{k_2})y'''(l,t)\dot{y}(l,t)-\\ & \varsigma k_3T_0(l)y'^4(l,t)-{\varsigma}(c-{\sigma_1})\int^l_0\dot{y}^2(z, t){\rm{d}}z+\\ & (2\varsigma\psi(l)-{\varsigma k_3T_0(l)})y'^3(l,t)\dot{y}(l,t)+\\ &{\varsigma k_2k_3T_0(l)}{y}'''(l,t)y'^3(l,t)-{\varsigma T_0(l)}\nu(t)\dot{y}(l,t)+\\ &{\varsigma k_2T_0(l)}y'''(l,t){y}'(l,t)-{\varsigma k_3T_0(l)}y'^3(l,t)\nu(t)-\\ &{\varsigma T_0(l)}\nu(t){y}'(l,t)+\frac{\varsigma}{\sigma_1} \int^l_0f^2(z,t){\rm{d}}z \end{aligned} $
(29) 其中, $ \delta_1 > 0 $.
对$ Y_f(t) $求导, 代入式(11)和式(14), 应用引理1, 可得
$ \begin{split} \dot{Y}_g(t)\le& -\varsigma k_4\mu^2(t)-\varsigma \nu(t)\triangle u-\varsigma k_1\nu^2(t)+\\& \varsigma T_0(l)\nu(t)y'(l,t)-\varsigma EI \nu(t)y'''(l, t)+\\& 2\varsigma \psi(l)\nu(t)y'^3(l,t)+\varsigma d_a \nu(t)\dot{y}(l,t) \end{split} $
(30) 对$ Y_g(t) $求微分, 代入式(4)并利用引理1, 有
$ \begin{aligned} \dot{Y}_f(t)\le & -l\lambda EI\phi(l) y'''(l,t){y}'(l,t)+\frac{\lambda \rho l\phi(l)}{2}\dot{y}^2(l,t)-\\ &\frac{3\lambda EI}{2}\int^l_0(\phi(z)+z\phi'(z)){y}^{{\prime\prime}2}(z, t){\rm{d}}z-\\ &\left[\frac{\lambda \rho}{2}(\phi(z)+z\phi'(z))-\frac{l\lambda c}{\sigma_2}\right]\int^l_0\dot{y}^2(z, t){\rm{d}}z-\\ &\bigg[\frac{\lambda }{2}(\phi(z)T_0(z)+z\phi'(z)T_0(z)-z\phi(z)T_0'(z))-\\ & {\lambda\sigma_2cl\phi^2(z)}-{\lambda\sigma_3l\phi^2(z)}\bigg]\int^l_0{y}^{{\prime}2}(z, t){\rm{d}}z-\\ & \frac{\lambda }{2}\int^l_0[3\phi(z)\psi'(z)+3z\phi'(z)\psi(z)-\\ &z\phi(z)\psi'(z)]{y}^{{\prime}4}(z, t){\rm{d}}z+\frac{3\lambda \phi(l)\psi(l)l}{2}y'^4(l,t)+\\ & \frac{l\lambda}{\sigma_3} \int^l_0f^2(x,t){\rm{d}}x+\frac{\lambda \phi(l)T_0(l) l}{2}y'^2(l,t) \end{aligned} $
(31) 其中, $ \sigma_2, \sigma_3 > 0 $.
将式(29)和式(30)代入式(28), 应用引理1, 可得
$ \begin{aligned} \dot{Y}(t)\le\;& -\varsigma\left( k_1+\frac{ T_0(l)}{2}-\frac{1}{\sigma_4}-\frac{|T_0(l)k_2-EI|}{2\sigma_5}-\right.\\ &\left.\frac{|T_0(l)-d_a|}{2\sigma_6}-\frac{| k_3T_0(l)-2 \psi(l)|\sigma_9}{2}\right)\nu^2(t)-\\ & \frac{3\lambda EI}{2}\int^l_0(\phi(z)+z\phi'(z)){y}^{{\prime\prime}2}(z, t){\rm{d}}z +\\ &{\varsigma}{\sigma_4}\triangle u^2-\varsigma\left( k_4-\frac{ T_0(l)}{2}\right)\mu^2(t)-\left(\frac{\varsigma T_0(l)}{2}-\right.\\ &\left.\frac{{|\varsigma T_0(l)k_2-l\lambda{EI}\phi(l)|}{\sigma_8}}{2}-\frac{\lambda \phi(l)T_0(l) l}{2}\right)\times\\ &y'^2(l,t)-\left(\varsigma k_3T_0(l)-\frac{3\lambda \phi(l)\psi(l)l}{2}\right)y'^4(l,t)-\\ &\left(\frac{\varsigma T_0(l)}{2}-\right.\frac{{\varsigma|T_0(l)-d_a|}{\sigma_6}}{2}-\\ &\left.\frac{{\varsigma|T_0(l)k_2-EI|}{\sigma_7}}{2}-\frac{{\varsigma|k_3T_0(l)-2\psi(l)|}{\sigma_{10}}}{2}-\right.\\ &\left.\frac{\lambda \rho l\phi(l)}{2}\right)\dot{y}^2(l,t)-\varsigma\left(\frac{ T_0(l)k^2_3}{2}-\right.\\ &\left.\frac{| k_3T_0(l)-2 \psi(l)|}{2\sigma_9}-\frac{ k_2k_3T_0(l)}{2\sigma_{11}}-\right.\\ &\left.\frac{|k_3T_0(l)-2\psi(l)|}{2\sigma_{10}}\right)y'^6(l,t)-\left(\frac{\varsigma T_0(l)}{2}-\right.\\ &\left.\frac{{\varsigma|T_0(l)k_2-EI|}{\sigma_5}}{2}-\frac{{\varsigma|T_0(l)k_2-EI|}}{2{\sigma_7}}-\right.\\ &\left.\frac{{|\varsigma T_0(l)k_2-l\lambda{EI}\phi(l)|}}{2{\sigma_8}}-\frac{\varsigma k_2k_3T_0(l)\sigma_{11}}{2}\right)\times\\ &\left.y'''^2(l,t)-\left[\frac{\lambda }{2}(\phi(z)T_0(z)+z\phi'(z)T_0(z)-\right.\right.\\ &\left.z\phi(z)T_0'(z))-\right.{\lambda\sigma_2cl\phi^2(z)}-{\lambda\sigma_3l\phi^2(z)}\bigg]\\ &\left.\int^l_0{y}^{{\prime}2}(z, t){\rm{d}}z+\left(\frac{\varsigma}{\sigma_1}+\frac{l\lambda}{\sigma_3}\right)\int^l_0f^2(z,t){\rm{d}}z-\right.\\ &\left.\bigg({\varsigma}c-{\varsigma}{\sigma_1}+\frac{\lambda \rho}{2}(\phi(z)+z\phi'(z))-\frac{l\lambda c}{\sigma_2}\right)\times\\ &\int^l_0\dot{y}^2(z, t){\rm{d}}z-\frac{\lambda }{2}\int^l_0[3\phi(z)\psi'(z)+\\ &3z\phi'(z)\psi(z)-z\phi(z)\psi'(z)]{y}^{{\prime}4}(z, t){\rm{d}}z \end{aligned} $
(32) 其中, $ \sigma_4\sim\sigma_{11} > 0, $选择恰当的参数值$ \varsigma, $ $ \lambda, $ $ k_i, $ $ i = 1, $ $\cdots, 4, \delta_j, j = 1, \cdots, 11, $满足下列条件:
$ \begin{split} \frac{\varsigma T_0(l)}{2}-\;&\frac{{|\varsigma T_0(l)k_2-l\lambda{EI}\phi(l)|}{\sigma_8}}{2}-\\ &\frac{\lambda \phi(l)T_0(l) l}{2}\ge 0 \end{split} \hspace{51pt}$
(33) $ \begin{split} \frac{\varsigma T_0(l)}{2}-\;&\frac{{\varsigma|T_0(l)-d_a|}{\sigma_6}}{2}-\frac{{\varsigma|T_0(l)k_2-EI|}{\sigma_7}}{2}-\\ &\frac{{\varsigma|k_3T_0(l)-2\psi(l)|}{\sigma_{10}}}{2}-\frac{\lambda \rho l\phi(l)}{2}\ge 0 \end{split} \hspace{20pt}$
(34) $ \begin{split} \frac{\varsigma T_0(l)}{2}-\;&\frac{{\varsigma|T_0(l)k_2-EI|}{\sigma_5}}{2}-\frac{{\varsigma|T_0(l)k_2-EI|}}{2{\sigma_7}}-\\ &\frac{{|\varsigma T_0(l)k_2-l\lambda{EI}\phi(l)|}}{2{\sigma_8}}-\frac{\varsigma k_2k_3T_0(l)\sigma_{11}}{2}\ge 0 \end{split} $
(35) $ \begin{split} \frac{ T_0(l)k^2_3}{2}-\;&\frac{| k_3T_0(l)-2 \psi(l)|}{2\sigma_9}-\\ &\frac{|k_3T_0(l)-2\psi(l)|}{2\sigma_{10}}-\frac{ k_2k_3T_0(l)}{2\sigma_{11}}\ge 0 \end{split} \hspace{11pt}$
(36) $ \begin{align} \varsigma k_3T_0(l)-\frac{3\lambda \phi(l)\psi(l)l}{2}\ge 0 \end{align} \hspace{86pt}$
(37) $ \begin{split} \omega_1 =& \min\{ {\varsigma}c-{\varsigma}{\sigma_1}-\frac{l\lambda c}{\sigma_2}+ \\& \frac{\lambda \rho}{2}(\phi(z)+z\phi'(z))\}>0 \end{split} \hspace{78pt}$
(38) $ \begin{aligned} \omega_2 = &\min\bigg\{\frac{\lambda}{2}(\phi(z)T_0(z)+z\phi'(z)T_0(z)-\\& z\phi(z)T_0'(z))-\lambda\sigma_2cl\phi^2(z)-\lambda\sigma_3l\phi^2(z) \bigg\}>0 \end{aligned} $
(39) $ \begin{split} \omega_3 = &\min\{3\phi(z)\psi'(z)+3z\phi'(z)\psi(z)-\\ &z\phi(z)\psi'(z)\} >0 \end{split} \hspace{32pt}$
(40) $ \begin{align} \omega_4 = \min\{\phi(z)+z\phi'(z)\} >0 \end{align}\hspace{67pt} $
(41) $ \begin{split} \omega_5 =\;& k_1+\frac{ T_0(l)}{2}-\frac{1}{\sigma_4}-\frac{| k_3T_0(l)-2 \psi(l)|\sigma_9}{2}-\\ &\frac{|T_0(l)k_2-EI|}{2\sigma_5}-\frac{|T_0(l)-d_a|}{2\sigma_6}>0 \end{split} $
(42) $ \begin{align} \omega_6 = k_4-\frac{ T_0(l)}{2} >0 \end{align} \hspace{105pt}$
(43) $ \begin{align} \alpha = \left(\frac{\varsigma}{\sigma_1}+\frac{l\lambda}{\sigma_3}\right)lF^2+{\varsigma}{\sigma_4}\varpi^2<+\infty \end{align} \hspace{33pt}$
(44) 结合式(33) ~(44), 可得
$ \begin{aligned} \dot{Y}(t) \le & \ \alpha-\omega_1\int^l_0\dot{y}^2(z, t){\rm{d}}z-\omega_2\int^l_0{y}^{{\prime}2}(z, t){\rm{d}}z-\\ & \frac{\lambda }{2}\omega_3\int^l_0{y}^{{\prime}4}(z, t){\rm{d}}z-\frac{3\lambda EI}{2}\omega_4\int^l_0{y}^{{\prime\prime}2}(z, t){\rm{d}}z-\\& \ \varsigma\omega_5\nu^2(t)-\varsigma\omega_6\mu^2(t)\le\\ & \ \delta_3[Y_e(t)+Y_f(t)]+\alpha \end{aligned} $
(45) 其中, $ \delta_3 = {\min}\left(\dfrac{2\omega_1}{{\varsigma}\rho}, \dfrac{2\omega_2}{{\varsigma}\overline{T}_0}, \dfrac{\lambda\omega_3}{\varsigma\overline{\psi}}, \dfrac{3\lambda\pi_4}{\varsigma}, \dfrac{2\pi_5}{m}, \dfrac{2\pi_6}{m}\right) $.
根据式(26)和式(45), 有
$ \begin{align} \dot{Y}(t)\le -\delta{Y}(t)+\alpha \end{align} $
(46) 其中, $ \delta = \delta_3/\delta_2 $.
定理1.针对执行器非光滑反向间隙−饱和约束特性的深海柔性立管系统, 如果系统初始条件是有界的且所选取参数满足约束条件式(33) ~(44), 在设计控制器(14)、假设1和假设2作用下, 闭环系统是一致有界稳定的.
证明.将式(27)乘以$ {\rm{e}}^{{\vartheta}t} $, 得出:
$ \begin{align} \frac{\partial}{\partial t}\left({Y}(t){\rm{e}}^{\delta t}\right)\le \alpha {\rm{e}}^{\delta t} \end{align} $
(47) 积分上式并变换, 有:
$ \begin{align} {Y}(t)\le Y(0){\rm{e}}^{-\delta t}+\frac{\alpha}{\delta}\left(1-{\rm{e}}^{-\delta t}\right)\le Y(0){\rm{e}}^{-\delta t}+\frac{\alpha}{\delta} \end{align} $
(48) 求助于$ Y_{e}(t) $, 式(19)和引理2, 可得
$ \begin{split} \frac{{\varsigma}\underline{T}_0}{2l}y^2(z,t)\le &\frac{{\varsigma}}{2}\int^l_0T_0(z){y}^{{\prime}2}(z,t){\rm{d}}z\le\\ &{Y_e(t)}\le\frac{1}{\delta_1}Y(t) \end{split} $
(49) 将式(48)代入式(49), 产生
$ \begin{split} \mid y(z,t)\mid \le \sqrt{\frac{2l}{{\varsigma}\delta_1\underline{T}_0}\left[Y(0){\rm{e}}^{-\delta t} +\frac{\alpha}{\delta}\right]}, \\ \forall (z,t) \in[0,l]\times[0,+\infty) \end{split} $
(50) 进一步得出
$ \begin{split} \underset{t\to\infty}{\mathop{\lim }} \,\left| y(z,t) \right| \le\sqrt{\frac{2l\alpha}{\varsigma{\underline{T}_0}{\delta}_{1}\delta}}, \ \ \ \forall z\in[0,l] \end{split} $
(51) 3. 数值仿真
为验证所设计控制器的性能, 本节在MATLAB软件中采用有限差分法[27-30]来近似闭环系统的数值解.柔性立管系统的参数为$ l = 1\; 000\, \rm{m}, $ $ \rho = 500\, \rm{kg/m}, $ $ c = 1.0\, \rm{Ns/m^2}, $ $ T_0(z) = 4.5\times10^5\times(1\; 000+z)\, \rm{N}, $ $\psi(z)=$ $ 1\times10^3 (1\; 000+z), $ $ EI $ = $ 1.5\times10^7\, {\rm N m^2}, ~{m}$ $=9.6\times10^6\, \rm{kg}, $ $ d_a = 1\; 000\, \rm{Ns/m}. $系统的初始条件描述为: $ y(z, 0) =$ $ \dfrac{12z}{l}, ~ \dot{y}(z, 0) = 0 $.
外部环境扰动$ d(t) $为
$ \begin{split} d(t) =\;& [3+0.8\sin(0.7t)+0.8\sin(0.5t)+\\& 0.8\sin(0.9t)]\times10^5 \end{split} $
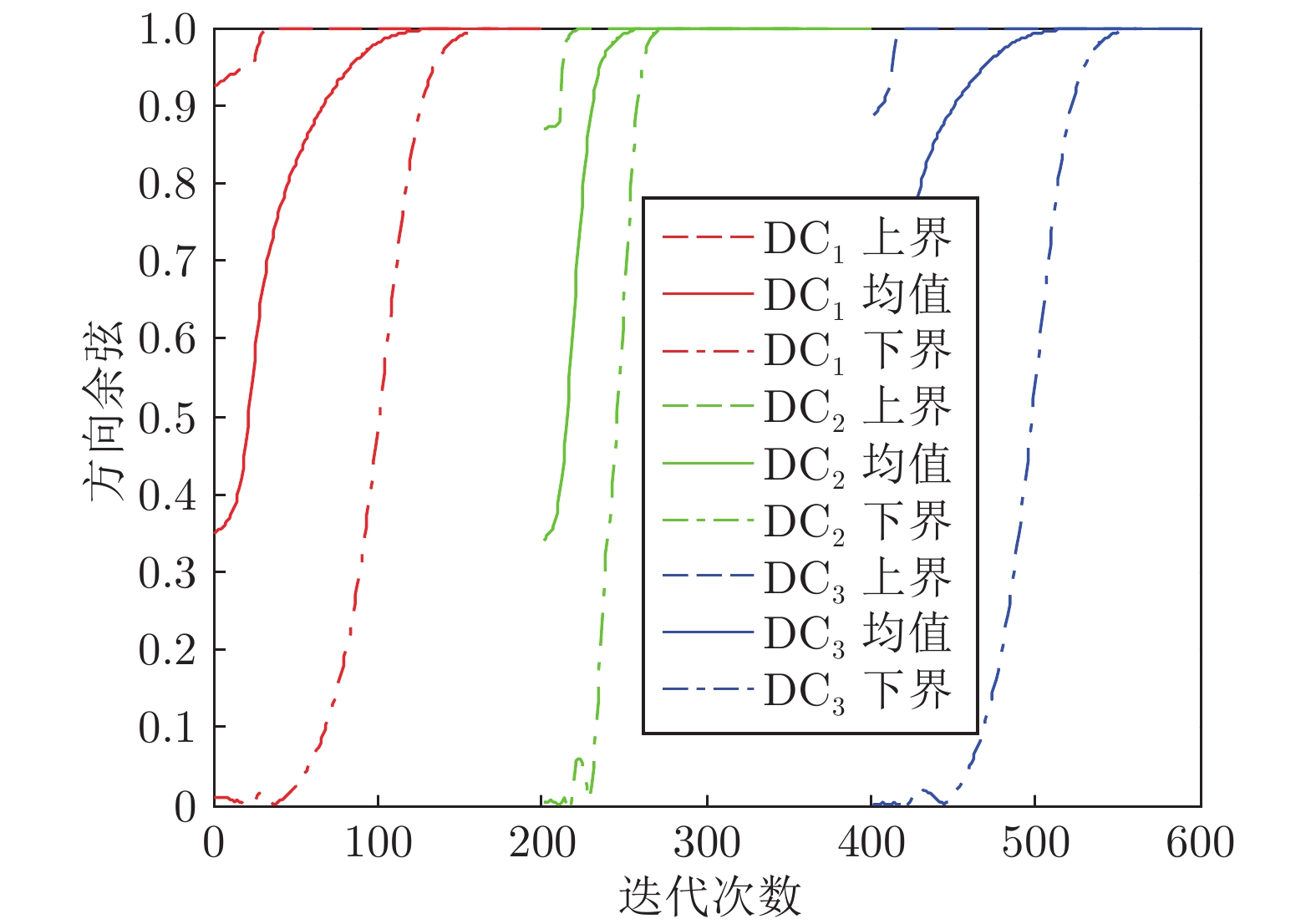
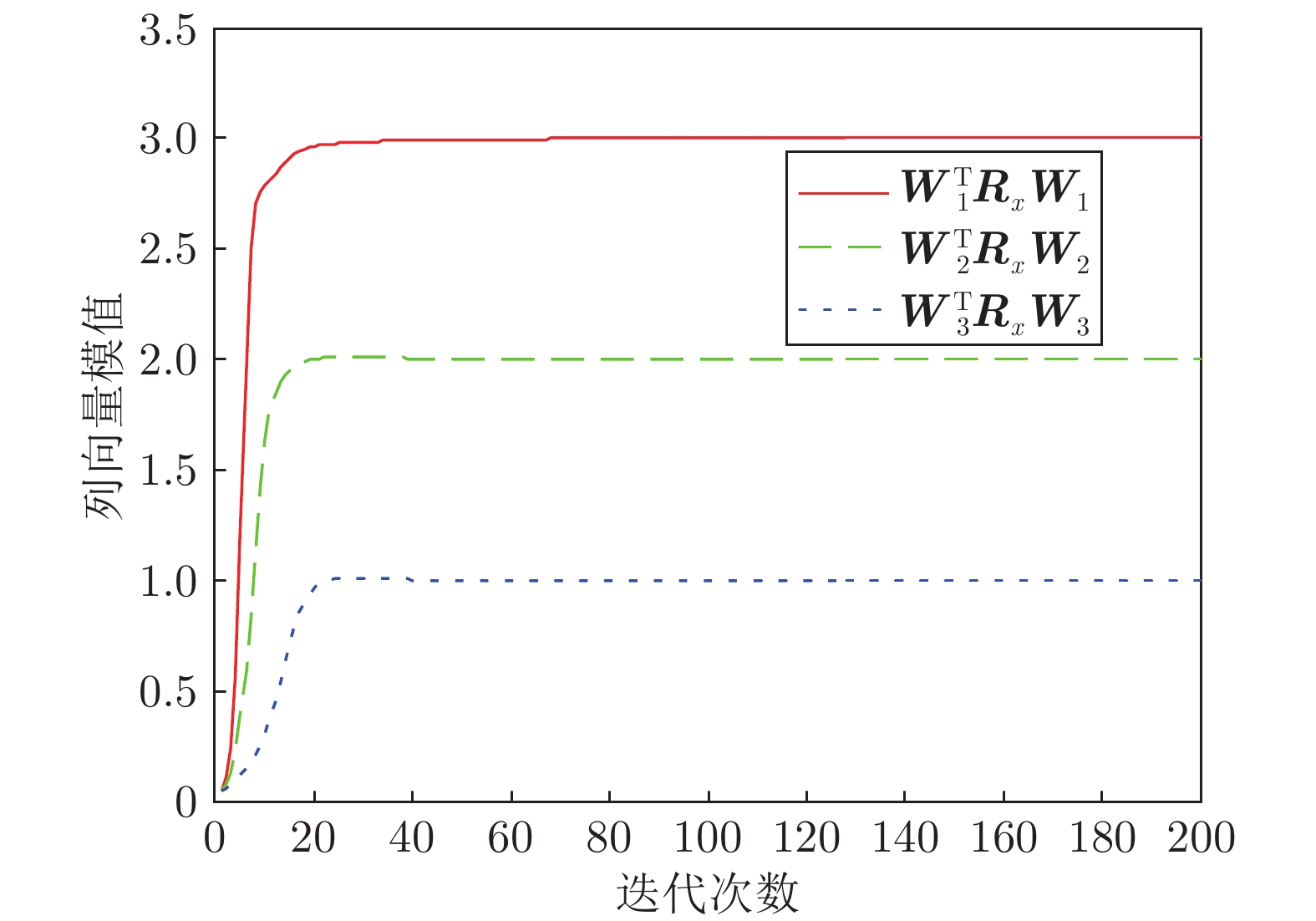
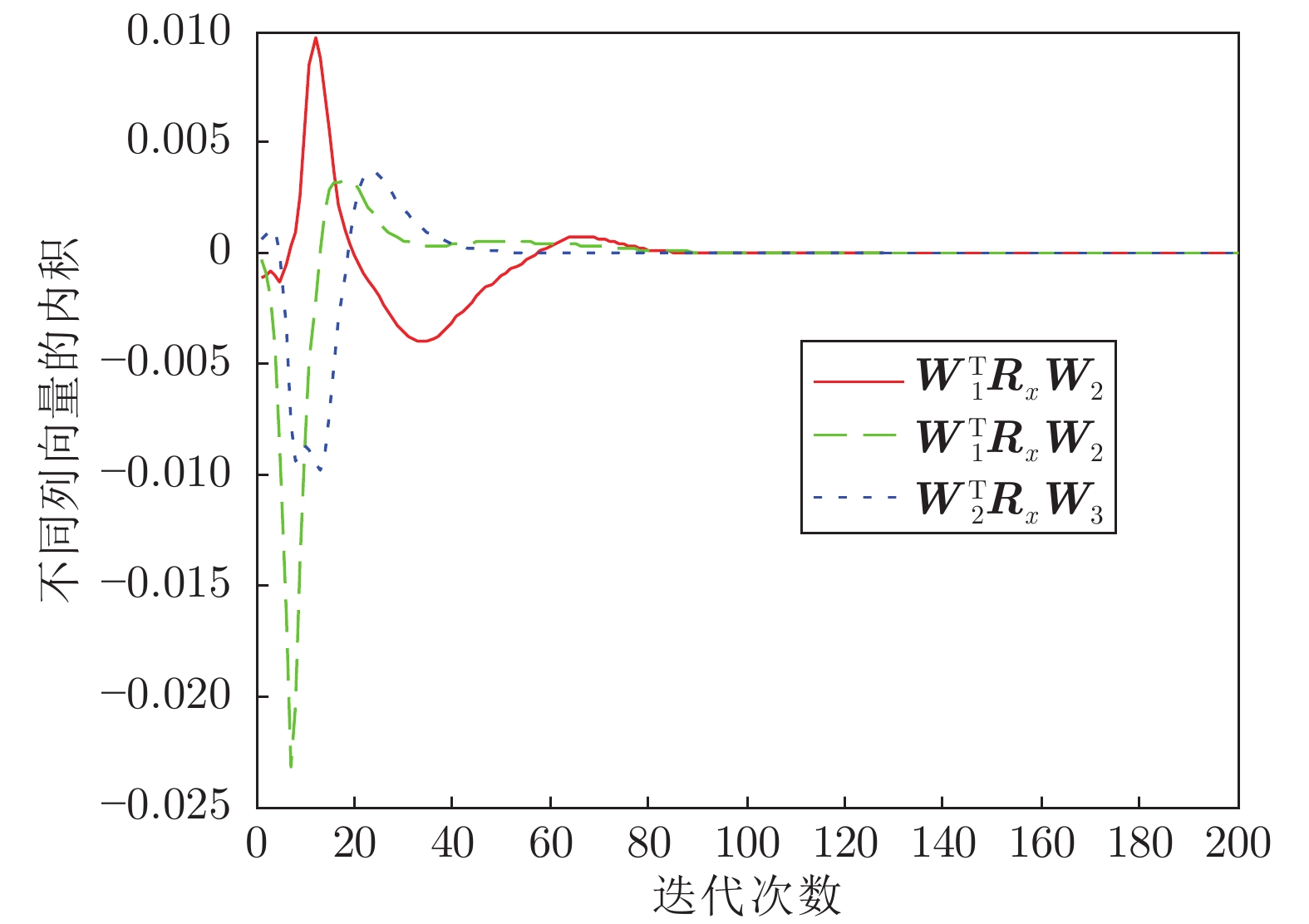
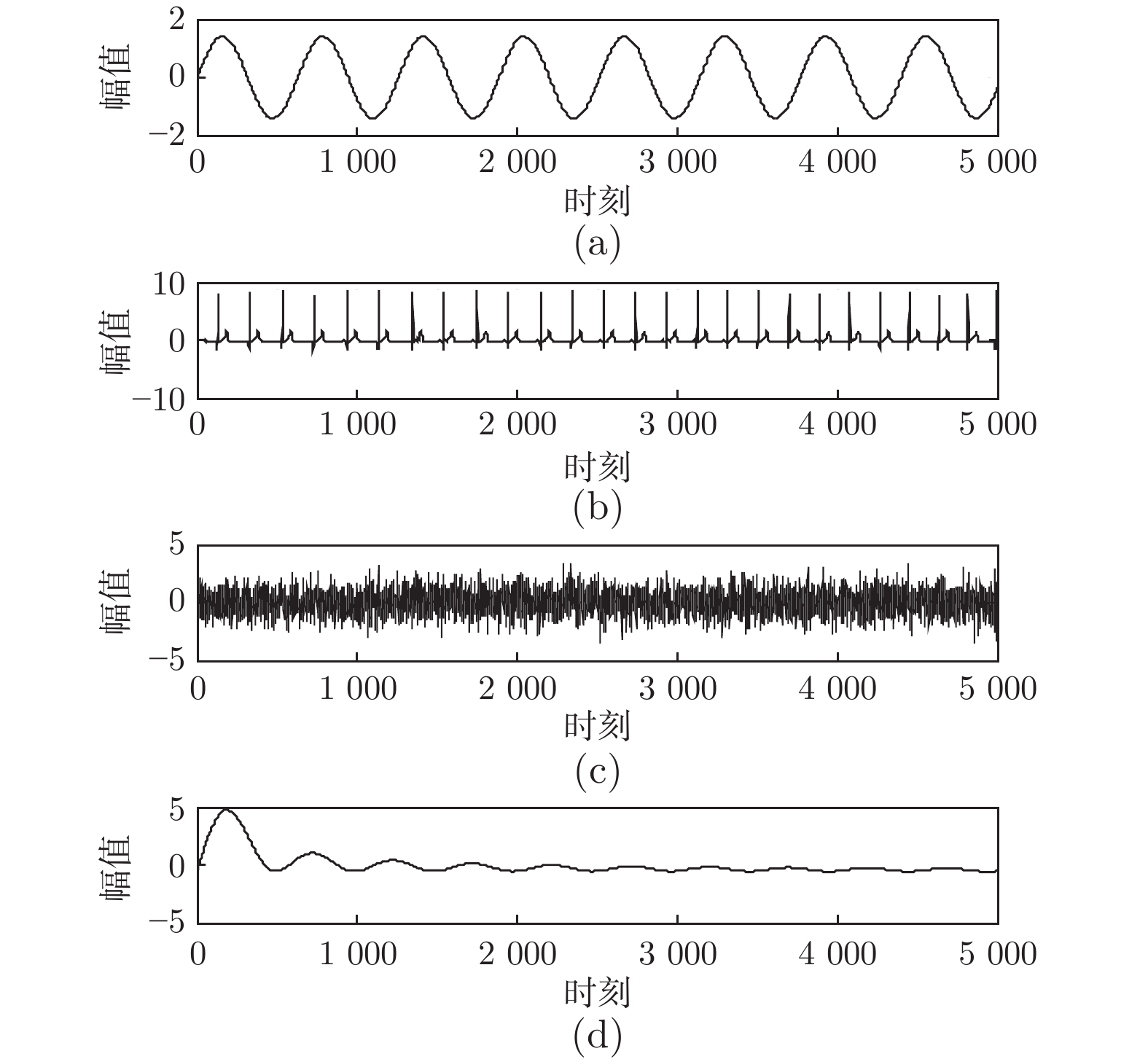
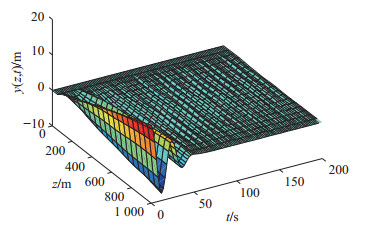
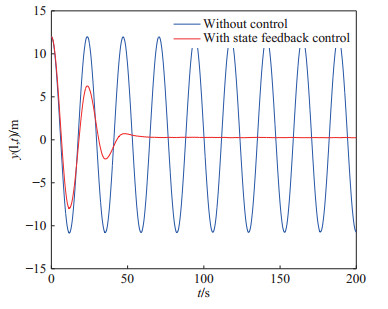
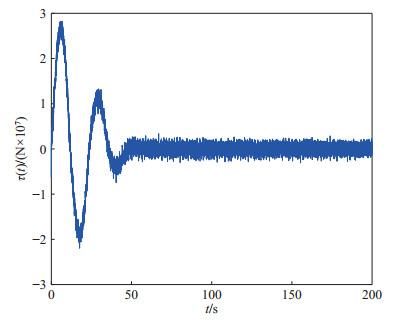
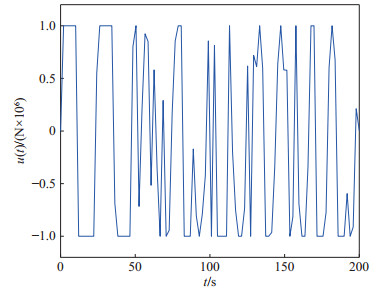
(52) 柔性立管系统在自由振动时, 即$ u(t) = 0 $, 图 2给出了其时空的表示.在所示设计控制器(14)作用下, 选取控制设计参数$ k_1 $ = $ 1\times10^7 $, $ k_2 = {1}/{60}, $ $ k_3= {1}/{225}, $ $ k_4 $ = $ 5\times10^8, $ $ a $ = $ 1\times10^6 $, $ b = 5~\times $ $10^6 $, 立管三维响应显示在图 3中. 图 4则给出了立管中部顶端$ (x = 1\; 000\; {\rm{m}}) $的二维偏移图, 图 5和图 6分别描绘了所设计的控制命令和反向间隙−饱和控制输入.
仿真图 2和图 3表明, 在外部扰动和执行器非光滑反向间隙−饱和约束条件下, 所设计控制器(14)能有效抑制立管振动; 由仿真图 4可得, 立管端点的偏移量稳定在平衡位置附近的小邻域; 仿真图 5和图 6得出, 控制器的输入是非线性的, 执行器非光滑反向间隙−饱和约束特性也相当地明显.根据上述分析, 可得如下结论:由于混合的输入非线性影响, 立管的振动偏移量需要相对长的收敛时间; 本文所构建的控制策略能较好地处理执行器非光滑反向间隙−饱和约束并能有效地抑制立管振动.
4. 结论
本文解决了具有执行器非光滑反向间隙−饱和约束特性的深海柔性立管边界控制问题.首先, 基于Lyapunov理论和边界控制技术, 采用辅助系统和函数在立管顶端构建了边界控制器以实现立管系统的振动抑制和输入非线性的补偿.其后, 应用严格的分析且没有离散化或简化系统的偏微分方程动力学, 证明了受控系统的一致有界性.最后所呈现的仿真结果验证了提出控制能较好地稳定立管系统并有效消除执行器非光滑反向间隙−饱和约束影响.下一步值得探索的研究方向可以为海洋柔性立管系统的有限时间稳定[31]以及基于不确定性和干扰估计[32]的控制设计.
-
表 1 两种算法的计算时间
Table 1 The time cost of the two algorithms
算法 时间 (ms) 所提算法 2.16 GDM算法 14.61 -
[1] Kong X Y, Du B Y, Feng X W, Luo J Y. Unified and self-stabilized parallel algorithm for multiple generalized eigenpairs extraction. IEEE Transactions on Signal Processing, 2020, 68: 3644-3659. doi: 10.1109/TSP.2020.2997803 [2] Rippl M, Lang B, Huckle T. Parallel eigenvalue computation for banded generalized eigenvalue problems. Parallel Computing, 2019, 88: 102542. doi: 10.1016/j.parco.2019.07.002 [3] Sun S L, Xie X J, Dong C. Multiview learning with generalized eigenvalue proximal support vector machines. IEEE Transactions on Cybernetics, 2019, 49(2): 688-697. doi: 10.1109/TCYB.2017.2786719 [4] Miyata T. A Riccati-type algorithm for solving generalized Hermitian eigenvalue problems. The Journal of Supercomputing, 2021, 77(2): 2091-2102. doi: 10.1007/s11227-020-03331-w [5] 郭亚宁, 林伟, 潘泉, 赵春晖, 胡劲文, 马娟娟. 基于推广流形学习的高分辨遥感影像目标分类. 自动化学报, 2019, 45(4): 720-729 doi: 10.16383/j.aas.2017.c170318Guo Ya-Ning, Lin Wei, Pan Quan, Zhao Chun-Hui, Hu Jin-Wen, Ma Juan-Juan. Generalized manifold learning for high resolution remote sensing image object classification. Acta Automatica Sinica, 2019, 45(4): 720-729 doi: 10.16383/j.aas.2017.c170318 [6] 陈晓云, 廖梦真. 基于稀疏和近邻保持的极限学习机降维. 自动化学报, 2019, 45(2): 325-333 doi: 10.16383/j.aas.2018.c170216Chen Xiao-Yun, Liao Meng-Zhen. Dimensionality reduction with extreme learning machine based on sparsity and neighborhood preserving. Acta Automatica Sinica, 2019, 45(2): 325-333 doi: 10.16383/j.aas.2018.c170216 [7] 孔祥玉, 冯晓伟, 胡昌华. 广义主成分分析算法及应用. 北京: 国防工业出版社, 2018.Kong Xiang-Yu, Feng Xiao-Wei, Hu Chang-Hua. General Principal Component Analysis and Application. Beijing: National Defense Industry Press, 2018. [8] Gao Y B, Kong X Y, Zhang Z X, Hou L A. An adaptive self-stabilizing algorithm for minor generalized eigenvector extraction and its convergence analysis. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10): 4869-4881 doi: 10.1109/TNNLS.2017.2783360 [9] Nguyen T D, Takahashi N, Yamada I. An adaptive extraction of generalized eigensubspace by using exact nested orthogonal complement structure. Multidimensional Systems and Signal Processing, 2013, 24(3): 457-483 doi: 10.1007/s11045-012-0172-9 [10] Li H Z, Du B Y, Kong X Y, Gao Y B, Hu C H, Bian X H. A generalized minor component extraction algorithm and its analysis. IEEE Access, 2018, 6: 36771-36779 doi: 10.1109/ACCESS.2018.2852060 [11] Kong X Y, Hu C H, Duan Z S. Principal Component Analysis Networks and Algorithms. Singapore: Springer, 2017. [12] Liu L J, Shao H M, Nan D. Recurrent neural network model for computing largest and smallest generalized eigenvalue. Neurocomputing, 2008, 71(16-18): 3589-3594 doi: 10.1016/j.neucom.2008.05.005 [13] Attallah S, Abed-Meraim K. A fast adaptive algorithm for the generalized symmetric eigenvalue problem. IEEE Signal Processing Letters, 2008, 15: 797-800 doi: 10.1109/LSP.2008.2006346 [14] Nguyen T D, Yamada I. Adaptive normalized quasi-newton algorithms for extraction of generalized Eigen-pairs and their convergence analysis. IEEE Transactions on Signal Processing, 2013, 61(6): 1404-1418 doi: 10.1109/TSP.2012.2234744 [15] Qiu J L, Wang H, Lu J B, Zhang B B, Du K L. Neural network implementations for PCA and its extensions. International Scholarly Research Notices, 2012, 2012: 847305. [16] Lewis D W. Matrix Theory. Singapore: World Scientific, 1991. [17] 杜柏阳, 孔祥玉, 冯晓伟. 次成分提取信息准则的加权规则方向收敛分析. 通信学报, 2020, 41(3): 25-32 doi: 10.11959/j.issn.1000-436x.2020014Du Bo-Yang, Kong Xiang-Yu, Feng Xiao-Wei. Direction convergence analysis of weighted rule for minor component extraction information criteria. Journal on Communications, 2020, 41(3): 25-32 doi: 10.11959/j.issn.1000-436x.2020014 [18] Möller R. Derivation of Coupled PCA and SVD Learning Rules From a Newton Zero-finding Framework, Computer Engineering, Faculty of Technology, Bielefeld University, Berlin, 2017. [19] Gao Y B, Kong X Y, Hu C H, Li H Z, Hou L A. A generalized information criterion for generalized minor component extraction. IEEE Transactions on Signal Processing, 2017, 65(4): 947-959 doi: 10.1109/TSP.2016.2631444 [20] Zhang W T, Lou S T, Feng D Z. Adaptive quasi-newton algorithm for source extraction via CCA approach. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(4): 677-689 doi: 10.1109/TNNLS.2013.2280285 期刊类型引用(18)
1. 翟漪璇,宋丽梅,贺瑾胜,朱新军. 低重叠率人体点云拼接方法研究. 应用激光. 2024(03): 204-213 .  百度学术
百度学术2. 毕淳锴,张远辉,付铎. 基于多视角热像图序列的物体表面温度场重建. 计量学报. 2024(07): 997-1006 .  百度学术
百度学术3. 王耀南,谢核,邓晶丹,毛建旭,李文龙,张辉. 智能制造测量机器人关键技术研究综述. 机械工程学报. 2024(16): 1-18 .  百度学术
百度学术4. 梁循,李志莹,蒋洪迅. 基于图的点云研究综述. 计算机研究与发展. 2024(11): 2870-2896 .  百度学术
百度学术5. 冯站银. 三维点云语义分割方法综述. 电视技术. 2023(03): 140-143+148 .  百度学术
百度学术6. 李颀,郭梦媛. 基于深度学习的休眠期苹果树点云语义分割. 江苏农业学报. 2023(05): 1189-1198 .  百度学术
百度学术7. 黄淞宣,李新春,刘玉珍. 邻域多维度特征点结合相关熵的点云配准. 激光与红外. 2023(08): 1163-1170 .  百度学术
百度学术8. 单铉洋,孙战里,曾志刚. RFNet:用于三维点云分类的卷积神经网络. 自动化学报. 2023(11): 2350-2359 .  本站查看
本站查看9. 马洁莹,田暄,翟庆,王丞. 基于点到面度量的多视角点云配准方法. 西安交通大学学报. 2022(06): 120-132 .  百度学术
百度学术10. 杨宜林,李积英,王燕,俞永乾. 基于NDT和特征点检测的点云配准算法研究. 激光与光电子学进展. 2022(08): 198-204 .  百度学术
百度学术11. 鲁斌,范晓明. 基于改进自适应k均值聚类的三维点云骨架提取的研究. 自动化学报. 2022(08): 1994-2006 .  本站查看
本站查看12. 陈亚超,樊彦国,樊博文,禹定峰. 基于相对几何不变性的点云粗配准算法研究. 计算机工程与应用. 2022(24): 233-238 .  百度学术
百度学术13. 庄仁诚,陈鹏,傅瑶,黄运华. 列车车轮三维结构光检测中的点云处理研究. 中国测试. 2021(02): 19-25 .  百度学术
百度学术14. 沈小军,于忻乐,王远东,程林,王东升,陈佳. 变电站电力设备红外热像测温数据三维可视化方案. 高电压技术. 2021(02): 387-395 .  百度学术
百度学术15. 杨贵强,李瑞,刘玉君,汪骥,周玉松. 最大相关熵的船体分段扫描数据配准算法. 中国造船. 2021(01): 183-191 .  百度学术
百度学术16. 元沐南,李晓风,李皙茹,许金林. 基于压缩感知的三维足型重建平台. 电子测量技术. 2020(09): 94-98 .  百度学术
百度学术17. 林伟,孙殿柱,李延瑞,沈江华. 复杂型面约束的点云配准序列确定方法. 小型微型计算机系统. 2020(09): 2012-2016 .  百度学术
百度学术18. 黄思捷,梁正友,孙宇,李轩昂. 单Kinect+圆盒的多视角三维点云配准方法研究. 现代计算机. 2020(31): 38-45 .  百度学术
百度学术其他类型引用(17)
-






 下载:
下载:

 下载:
下载: