Bifurcation Dynamics of Large-scale Neural Networks Composed of Super Multi-ring Networks
-
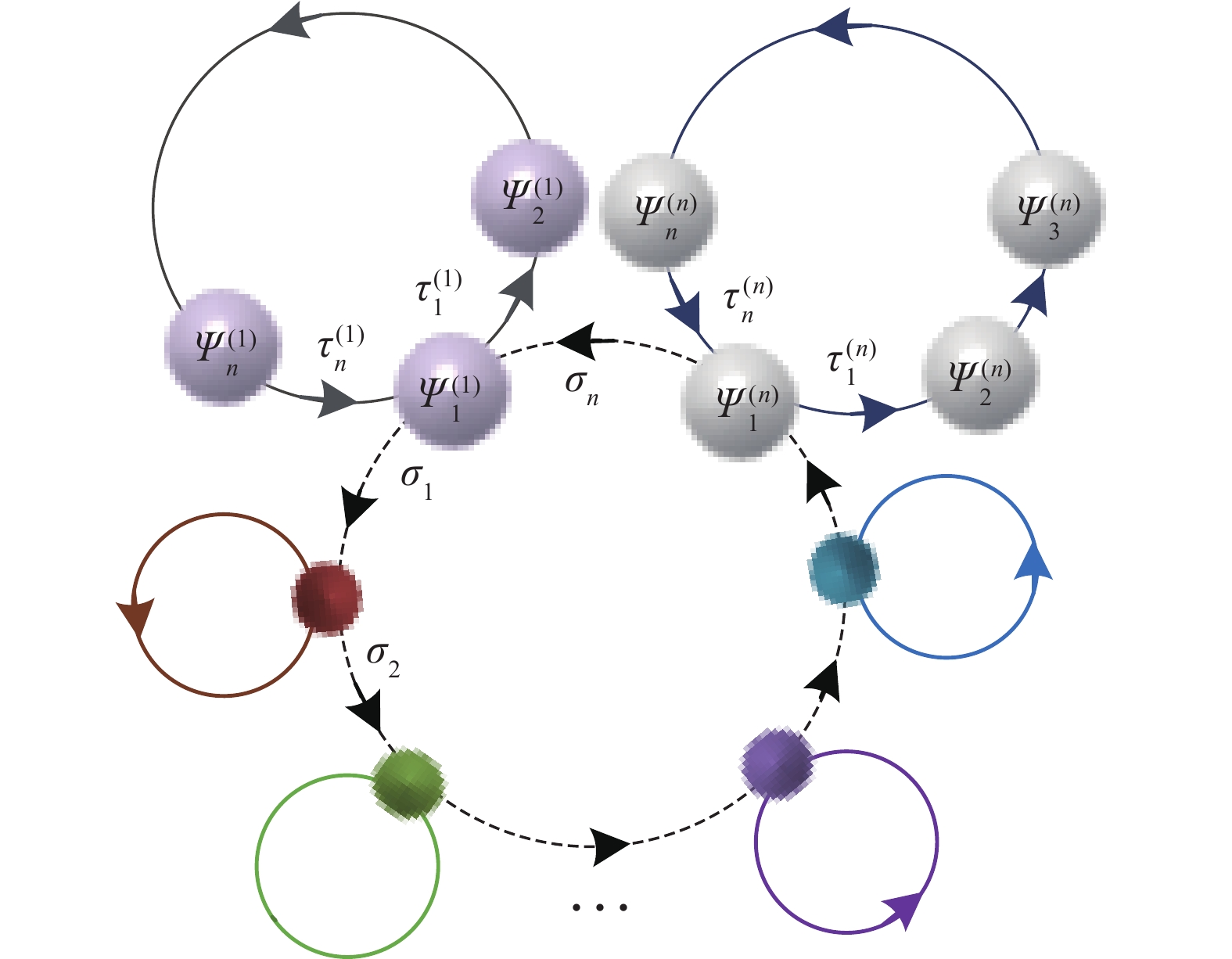
摘要: 目前绝大多数神经网络分岔动力学局限于结构简单、低维少节点模型, 这与真实的大规模神经网络系统相去甚远. 因此, 研究大量神经元耦合的高维神经网络模型更具实际应用价值. 环状及辐射状结构在神经网络中普遍存在, 提出了一类大规模超环时滞神经网络模型, 结构包含一个大环和任意多个小环, 并且每个环上拥有任意多个神经元. 运用特征值法和分岔理论, 选取时滞为分岔参数, 给出了该超环神经网络模型的稳定性条件和Hopf分岔判据. 数值仿真结果, 验证该理论结果的正确性.Abstract: At present, most bifurcation dynamics of neural networks are limited to simple structure, low dimension and few nodes, which are far from the real large-scale neural network system. Therefore, it is more practical to study the high-dimensional neural network model with a large number of neurons coupling. Ring and radial structures are ubiquitous in neural networks. This paper presents a class of large-scale neural networks with super-ring structure and delays, which consists of a large ring and any number of small rings, and each ring has any number of neurons. By using the eigenvalue method and bifurcation theory, the stability condition and Hopf bifurcation criterion of the super-ring neural network model are obtained by taking the time delay as bifurcation parameter. The correctness of the theoretical results is verified by numerical simulation.
-
Key words:
- Neural network /
- super-ring structure /
- time delay /
- stability /
- Hopf bifurcation
-
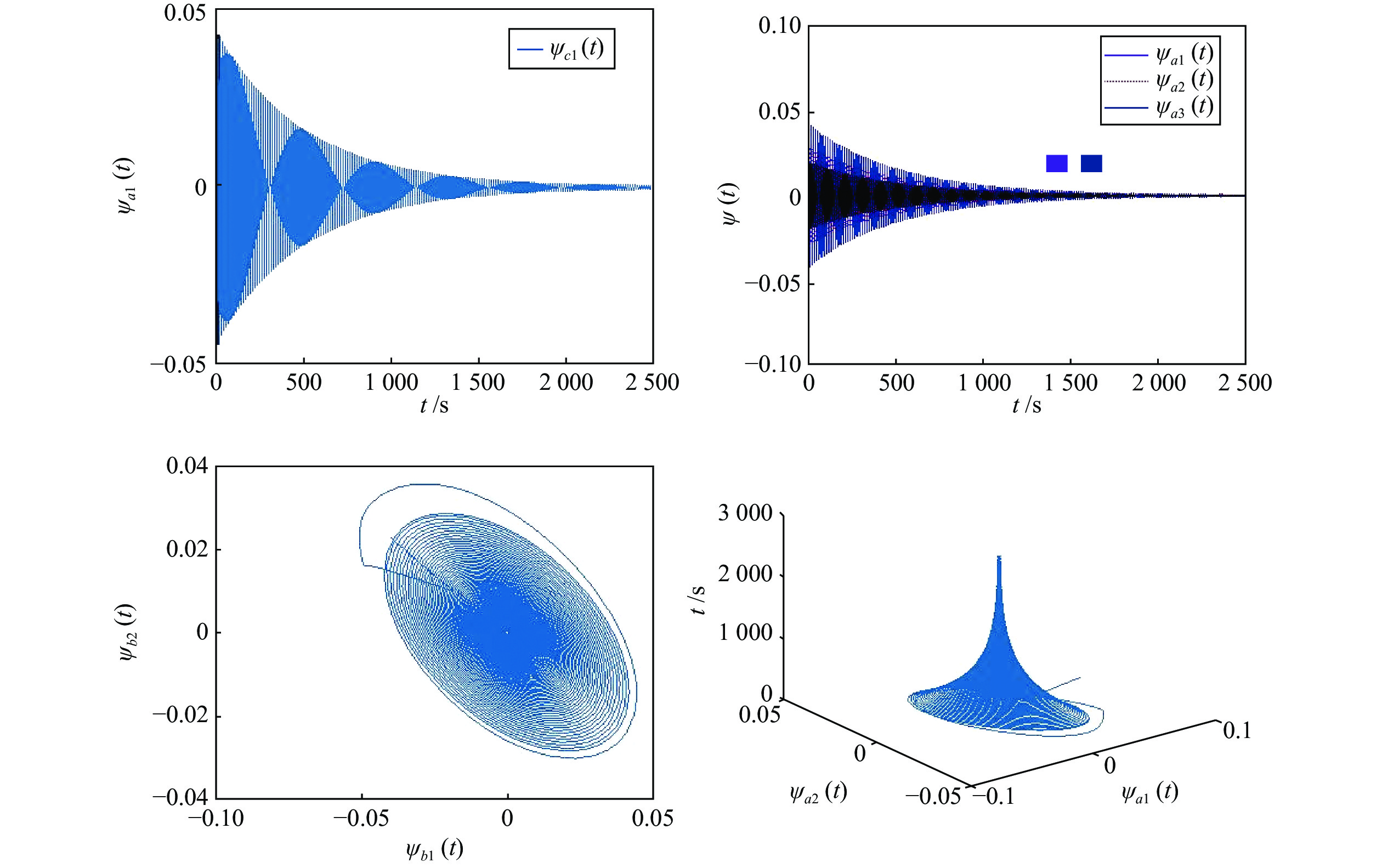
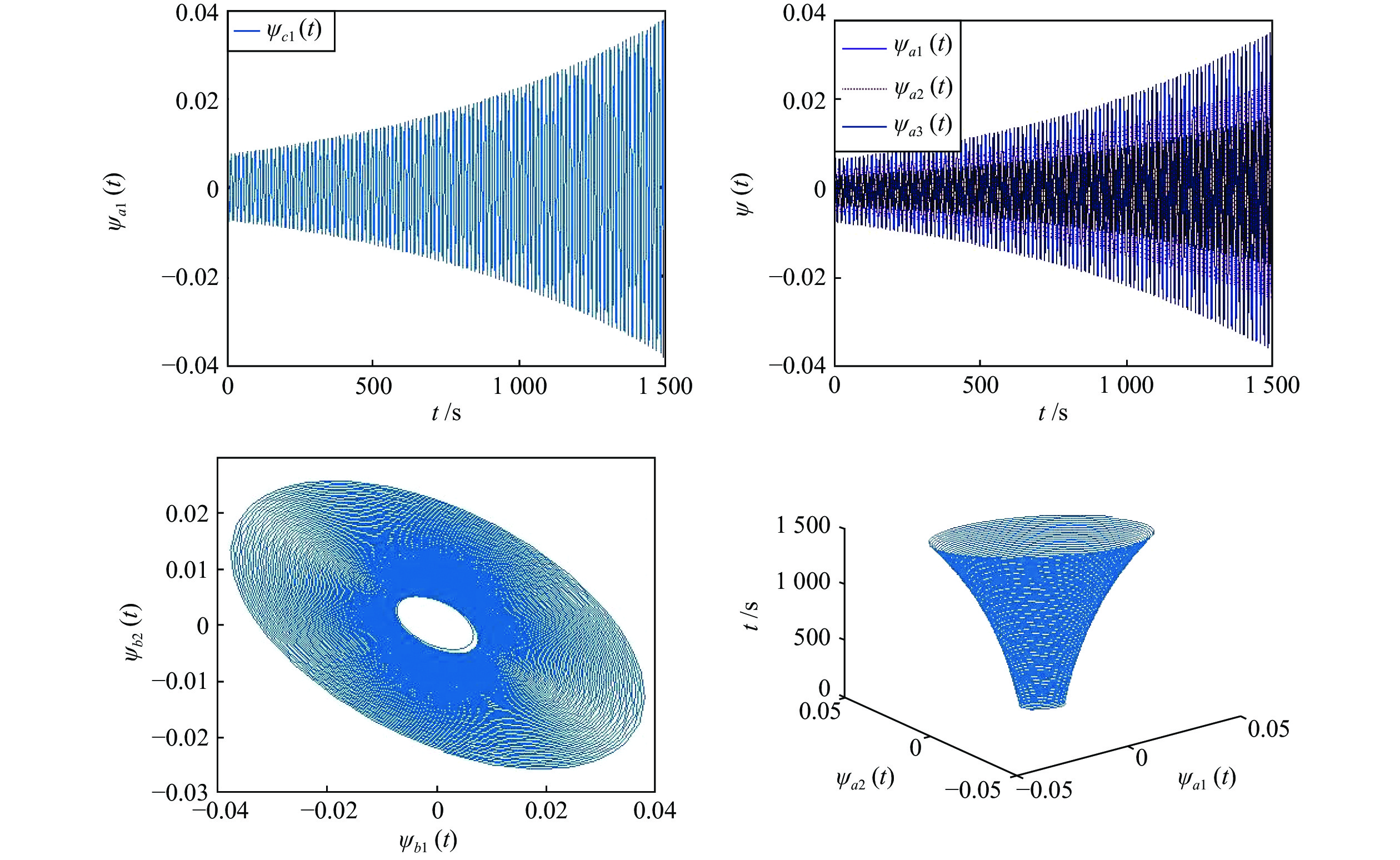
表 1 网络(15)的初始参数设定表
Table 1 Initial parameter setting table for network (15)
参数 $\rho $ $v_j^{(k)},\forall j,k = {1,2,3}$ 初始值 0.75 -0.6 表 2 结构变化影响分岔点位置情况表
Table 2 Table of the influence of structural change on the location of bifurcation points
环的个数 结构简图 神经元个数 分岔点 3 
6 16.2 4 
9 3.22 5 
12 2.08 -
[1] 张耀中, 胡小方, 周跃, 段书凯. 基于多层忆阻脉冲神经网络的强化学习及应用. 自动化学报, 2019, 45(8): 1536-1547.Zhang Yao-Zhong, Hu Xiao-Fang, Zhou Yue, Duan Shu-Kai. A novel reinforcement learning algorithm based on multilayer memristive spiking neural network with applications. Acta Automatica Sinica, 2019, 45(8): 1536-1547. [2] 杨刚, 王乐, 戴丽珍, 杨辉. 基于连接自组织发育的稀疏跨越-侧抑制神经网络设计. 自动化学报, 2019, 45(4): 808-818.Yang Gang, Wang Le, Dai Li-Zhen, Yang Hui. Design of sparse span-lateral inhibition neural network based on connection self-organization development. Acta Automatica Sinica, 2019, 45(4): 808-818. [3] Zhen W, Li L, Li Y, Cheng Z. Stability and Hopf bifurcation of a three-neuron network with multiple discrete and distributed delays. Neural Processing Letters, 2018, 48(5): 1481-1502. [4] Cheng Z, Xie K, Wang T, Cao J. Stability and Hopf bifurcation of three-triangle neural networks with delays. Neurocomputing, 2018, 322: 206-215. doi: 10.1016/j.neucom.2018.09.063 [5] Xu C, Liao M, Li P, Guo Y. Bifurcation analysis for simplified five-neuron bidirectional associative memory neural networks with four delays. Neural Processing Letters, 2019, 50: 2219–2245. doi: 10.1007/s11063-019-10006-y [6] Wang T, Cheng Z, Bu R, Ma R. Stability and Hopf bifurcation analysis of a simplified six-neuron tridiagonal two-layer neural network model with delays. Neurocomputing, 2019, 332: 203-214. doi: 10.1016/j.neucom.2018.12.005 [7] Bootan R, Yuliya N, Konstantin B. Dynamics of unidirectionally-coupled ring neural network with discrete and distributed delays. Journal of Mathematical Biology, 2020, 80: 1617-1653. doi: 10.1007/s00285-020-01475-0 [8] Xu C J, Liao M X, Li P L, Guo Y, Xiao Q M, Yuan S. Influence of multiple time delays on bifurcation of fractional-order neural networks. Applied Mathematics and Computation, 2019, 361: 565-582. doi: 10.1016/j.amc.2019.05.057 [9] Ali M S, Narayanan G, Shekher V, Alsulami H, Saeed T. Dynamic stability analysis of stochastic fractional-order memristor fuzzy BAM neural networks with delay and leakage terms. Applied Mathematics and Computation, 2020, 369: 124896 [10] Li Z, Huang C, Zhang Y. Comparative analysis on bifurcation of four-neuron fractional ring networks without or with leakage delays. Advances in Difference Equations, 2019, 179: 1-22. [11] Yao Y, Xiao M, Cao J. Stability switches and Hopf bifurcation of a neuron system with both leakage and distributed delays. Neural Processing Letters, 2019, 50(2): 341-355. [12] Zhang Z Z, Yuan H Z. Hopf bifurcation in a delayed predator-prey system with modified Leslie-Gower and Holling-type III schemes. Acta Automatica Sinica, 2013, 5: 610-616. [13] Wang H P, Li J, Zhang K. Stability and Hopf bifurcation of the maglev system with delayed speed feedback control. Acta Automatica Sinica, 2007, 8: 829-834. [14] Dong T, Bai J Q, Yang L. Bifurcation analysis of delayed complex-valued neural Network with diffusions. Neural Processing Letters, 2019, 50(2): 1019-1033. doi: 10.1007/s11063-018-9899-0 [15] Elowitz M B, Leibler S. A synthetic oscillatory network of transcriptional regulators, Nature, 2000, 403(6767): 335−338 [16] Hassard B D, Kazarinoff N D, Wan Y H. Theory and applications of Hopf Bifurcation. Cambridge: Cambridge University Press, 1981. [17] Xiao M, Zheng W X, Cao J. Hopf bifurcation of an (n+1)-neuron bidirectional associative memory neural network model with delays. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(1): 118-132. doi: 10.1109/TNNLS.2012.2224123 [18] Huang C, Cao J, Xiao M, Alsaedi A, Hayat T. Effects of time delays on stability and Hopf bifurcation in a fractional ring-structured network with arbitrary neurons. Communications in Nonlinear Science and Numerical Simulation, 2018, 57: 1-13. doi: 10.1016/j.cnsns.2017.09.005 [19] Milo R, Shen O S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U. Network motifs: Simple building blocks of complex networks, Science, 2002, 298 [20] 杨华. 矩阵与线性方程组的图解法. 天津: 南开大学, 2007.Yang Hua. A Graphical Method for Matrices and Systems of Linear Equations. Tianjin: Nankai University, 2007. [21] 胡寿松. 自动控制原理. 北京: 科学出版社, 2013. 95−97Hu Shou-Song. Automatic Control Theory. Beijing: Science Press, 2013. 95−97 -




 下载:
下载: