Backstepping-based Output Feedback Boundary Control for Coupled Fractional Reaction-diffusion Systems
-
摘要: 针对具有空间依赖耦合系数的分数阶反应扩散系统, 利用反步法设计了基于观测器的边界输出反馈控制器, 证明了观测增益和控制增益核函数矩阵方程的适定性. 针对误差系统和输出反馈的闭环系统, 利用分数阶Lyapunov方法分析了系统的Mittag-Leffler稳定性, 且利用Wirtinger不等式改进了耦合系统稳定的条件. 当系统具有空间依赖的耦合系数时, 难以求得控制增益和观测增益核函数的解析解, 为此, 给出了核函数偏微分方程的数值解方法. 数值仿真验证了理论结果.Abstract: An observer-based boundary output feedback controller is designed by backstepping method for fractional reaction-diffusion systems with space-dependent coupling coefficients. The well-posednesses are proved for the kernel function matrix equations of the observer gains and control gains. For the error system and close-loop system of output feedback, the Mittag-Leffler stabilities of the systems are analyzed by the fractional Lyapunov method, and the stability conditions of the coupled systems are improved by using the Wirtinger＇s inequality. For the system with spatially-varying coupling coefficients, it is difficult to obtain analytical solutions of the kernel functions for the controller and the observer. Therefore, numerical methods of partial differential equations of the kernel functions are given. Numerical simulations verify the theoretical results.
-
耦合分数阶反应扩散系统中包含多个反常扩散的系统分量, 各系统分量在扩散的同时发生反应并相互转化, 这种耦合性在反应扩散系统中是普遍存在的[1]. 与经典的高斯扩散不同, 反常扩散过程表现出幂率(Power law)和重尾(Heavy-tailed)分布的特征, 其见于多种物理场景中, 如连续时间随机游走[2]、通过多孔介质的扩散等[3], 并广泛应用于物理、生物、工程等许多领域[4-6]. 耦合分数阶反应扩散系统作为一种典型的分布参数系统, 在整个空间区域上进行测量和控制通常是很困难的. 实际上, 在很多复杂的应用场景中, 如高温、高腐蚀, 或涉及液体流动的应用, 受到经济或技术条件的限制, 通常在系统边界上进行测量和控制, 其成本更低且容易实现. 因此, 使用边界测量值设计输出反馈的边界控制器具有重要的理论意义和应用价值. 本文主要针对一类带有空间依赖耦合系数的分数阶反应扩散系统, 利用反步法研究其边界输出反馈控制问题(如图1所示).
反步法(Backstepping)是一种稳定动态系统的特殊方法, 其主要思想是: 寻找合适的核函数构造可逆的反步变换, 将原系统映射到一个稳定的目标系统, 再导出使原系统稳定的控制器和相应的控制增益. 将反步法应用于偏微分方程(Partial differential equations, PDEs)边界控制问题, 已经取得许多重要成果[7-10]. 早在2003年, Liu[7]利用反步法研究了一类不稳定热方程的边界反馈镇定问题, 其中控制增益核函数是一个连续函数, 突破了此前基于离散化的方法. 随后, Smyshlyaev等[8]深入研究了一类抛物型偏积分微分方程的边界控制问题, 证明了核函数方程的适定性并给出了数值解和特定条件下的解析解. 在文献[9]中, 利用边界测量设计了指数收敛的观测器, 实现了输出反馈控制, 同时考虑了传感器与执行器并列和非并列的情况. 关于PDEs反步法的更多内容可参见文献[11-12].
近年来, 耦合PDEs反步边界控制成为新的研究热点[13-18]. Baccoli等[13]利用反步法解决了常系数耦合的反应扩散系统镇定问题, 针对扩散系数相同和相异两种情况分别设计了基于状态反馈的边界控制器, 并得到了核函数矩阵的级数解. Orlov等[16]系统地研究了常系数耦合反应扩散系统的状态反馈控制、观测器设计和输出反馈控制等一系列问题. Liu等[15]研究了基于观测器的常系数耦合反应扩散系统边界输出反馈控制, 并利用Poincaré不等式改进了文献[13]的结果. 针对耦合反应扩散方程的研究进一步推广到具有空间依赖参数的情形[17]以及输出调节问题[18].
最近几年, 分数阶反应扩散系统的边界控制问题引起了研究者的关注[19-28]. Ge等[19]应用PDEs反步法[8, 11]研究了具有Dirichlet和Neumann边界的分数阶反应扩散系统的边界控制问题, 证明了闭环系统的Mittag-Leffler稳定性[29-30]. 随后, 针对一类半线性时间分数阶扩散系统研究了Luenberger型观测器的设计[20], 然后又推广到系统参数随空间变化的情形[22]和事件触发控制[23]. Chen等[24]研究了带有混合或Robin边界条件的分数阶反应扩散系统的边界控制问题, 并推广到扩散系数随空间变化(各向异性)的情形[26], 然后又研究了观测器设计[25]和输出反馈控制[27]等问题. Zhou等[28]深入研究了一类不稳定的时间分数阶反应扩散方程的边界反馈镇定问题, 同时考虑了Dirichlet边界和Neumann边界控制, 采用Riesz基方法和分数阶Lyapunov方法[29]证明了闭环系统解的存在唯一性和Mittag-Leffler稳定性. 目前, 针对耦合分数阶扩散系统边界控制的研究还很少. Ge等[21]针对带有空间依赖参数的耦合半线性反常亚扩散(Subdiffusion)系统, 利用反步法设计了基于观测器的输出反馈控制器, 并证明了闭环系统的Mittag-Leffler稳定性. 在假设设计参数与核函数矩阵同为对角矩阵的条件下, 得到了核函数矩阵方程的解析解, 并推广了文献[13, 15-16]的结果. 然而, 一方面, 上述研究结果中设计参数的选择范围仍存在改进的空间; 另一方面, 为得到核函数的解析解, 需要假设核函数矩阵为对角阵或数量阵, 或者满足特定的不等式, 这在一定程度上增加了选择设计参数的难度. 同时, 当系统的耦合系数随空间变化时, 很难求得核函数矩阵方程的解析解[8]. 这些问题在一定程度上限制了该方法的应用.
鉴于以上考虑, 本文利用PDEs反步边界控制方法, 针对具有空间依赖耦合系数的分数阶反应扩散系统, 设计基于边界测量的观测器和输出反馈控制器, 实现边界测量、边界控制的输出反馈控制系统. 利用Wirtinger不等式[31]改进控制参数满足的条件, 扩大其取值范围. 针对包含空间依赖耦合系数的控制增益和观测增益核函数矩阵方程, 在分析解的适定性的基础上给出数值解法, 在无需假设核函数矩阵结构的条件下直接求解, 从而简化设计参数的选取方法. 最后, 利用数值仿真验证理论结果.
1. 系统模型与问题描述
考虑
$ n $ 个分数阶反应扩散系统组成的耦合系统$$ \begin{split} {_0^C D_t^\alpha}{\boldsymbol{Z}}(x,t) =\; &A{\boldsymbol{Z}}_{xx}(x,t) + \Phi(x){\boldsymbol{Z}}(x,t), \\ & \qquad\qquad\quad\qquad(x,t) \in \Omega \end{split} $$ (1) 具有Dirichlet-Robin 型混合边界条件
$$ {{{\boldsymbol{Z}}_x}}(0,t) = B{\boldsymbol{Z}}(0,t), \quad t>0 $$ (2) $$ \; {\boldsymbol{Z}}(1,t) = {\boldsymbol{U}}(t),\qquad\; \quad t>0\; $$ (3) 其中,
$\Omega = (0,1)\times(0,\infty)$ ,${\boldsymbol{Z}}(x,t) = [z_1(x,t), \cdots, z_n(x,$ $t)]^{{\rm T}}\in [L^2(0,1)]^n $ 为系统状态,$ x $ 和$ t $ 分别为空间和时间变量. 这里,$ L^2(0,1) $ 表示所有$ [0,1] $ 上平方可积函数组成的Hilbert空间, 其范数定义为$\lVert z(x,t) \rVert =$ $ \big( \int_0^1 z^2(x,t) {{\,{\rm d}}x}\big)^{1/2} $ .$ [L^2(0,1)]^n $ 为n个L2(0, 1)空间的直积, 其范数定义为$\lVert {\boldsymbol{Z}}(x,t) \rVert_{2,n} = \big( \sum_{i = 1}^n \lVert z_i(x,t) \rVert^2 \big)^{1/2}$ . Caputo时间分数阶导数$ {_0^C D_t^\alpha}(\cdot) $ 定义为[32]$$ {_0^C D_t^\alpha}z(x,t) = \frac{1}{\Gamma(1-\alpha)} \int_0^t \frac{1}{(t-\tau)^\alpha} \frac{\partial z(x,\tau)}{\partial \tau} {{\,{\rm d}}\tau} $$ 其中, 阶次
$ \alpha \in (0,1) $ 为常数,$ \Gamma(\cdot) $ 为Gamma函数,$ x \in (0,1) $ ,$ t\in (0,\infty) $ . 若令$ \alpha = 1 $ , 系统(1) ~ (3)退化为经典的(整数阶)耦合反应扩散系统[13-18]. 扩散系数矩阵$ A = aI \in {{\bf{R}}^{n \times n}} $ ,$ a>0 $ 为常数,$ I $ 为适当维数的单位矩阵.$ \Phi(x) = [\phi_{ij}(x)]_{n \times n}\in [C^1(0,1)]^{n \times n} $ 为空间依赖的耦合反应项系数(矩阵), 其中$ \phi_{ij}(x) $ 表示系统状态分量$ z_j(x,\cdot) $ 对$ z_i(x,\cdot) $ 的耦合作用,$ i,j = 1,\cdots,n $ . 矩阵$ B = bI \in { {\bf{R}}^{n \times n}} $ ,$ b>0 $ 为常数. 本文假设测量和控制均位于系统的边界上, 其中$ {\boldsymbol{Z}}(0,t) $ 作为测量输出,$ {\boldsymbol{Z}}(1,t) $ 作为控制输入$ {\boldsymbol{U}}(t) = $ $[u_1(t),\cdots,u_n(t)]^{{\rm T}}\in { {{\bf{R}}^n}} $ .当
$\Phi(x) = {\rm diag}{\lbrace \varphi_{11}(x),\cdots,\varphi_{nn}(x)\rbrace}$ 为对角阵时, 系统(1) ~ (3)中各分量为相互独立的时间分数阶反应扩散系统, 各分量之间没有耦合. 根据文献[33], 每个开环($ u_i(t)\; = \;0 $ )分量稳定的充要条件是$\big\lvert \arg\big( {\rm spec} \big( {{\cal{A}}} + \varphi_{ii}(x) \big) \big) \big\rvert > {\pi\alpha}/{2}$ , 其中, 算子$ {\cal{A}} $ 定义为$ ({\cal{A}} z)(x,t) = a \dfrac{\partial^2 z(x,t)}{\partial x^2} $ ,$ {\rm Dom}({\cal{A}}) = \{ z \in L^2(0,1) \mid z, z_x$ 绝对连续,$z_{xx} \in L^2(0,1),$ 且满足$z_x(0) = bz(0), z(1) =$ $0 \} $ . 显然, 若$ \varphi_{ii}(x) $ 足够大, 则系统分量$ z_i(x,t) $ 是不稳定的. 一般地, 与整数阶耦合反应扩散系统[13-18]类似, 在系统(1) ~ (3)中, 若各个系统分量之间存在耦合, 且矩阵$ S[\Phi(x)] $ 具有足够大的正特征值, 则对应的开环系统($ {\boldsymbol{U}}(t) = 0 $ )具有任意多个不稳定的特征值[1, 28], 这里$ S[X] = (X+X^{{\rm T}})/2 $ 表示任意方阵$ X $ 的对称部分. 本文的目的是针对耦合分数阶反应扩散系统(1) ~ (3)设计观测器, 并在此基础上设计基于观测器的输出反馈控制器, 从而使闭环系统(1) ~ (3) Mittag-Leffler稳定[29].为了便于讨论, 下面给出分数阶动态系统平衡点和Mittag-Leffler稳定性的定义.
定义1 (平衡点[30]). 常数
$ z_0 $ 是Caputo分数阶动态系统$ {_0^C D_t^\alpha}z(t) = f(t,z) $ 的平衡点, 当且仅当$ f(t,z_0) = 0 $ .由定义1可知,
$ {\boldsymbol{Z}}(x,\cdot) = 0 $ 是系统(1) ~ (3)的平衡点.定义2 (Mittag-Leffler稳定性[29-30]). 系统
$ {_0^C D_t^\alpha} {\boldsymbol{z}}(t) = f(t,{\boldsymbol{z}}) $ 的解是Mittag-Leffler稳定的, 如果$$ \lVert {\boldsymbol{z}}(t) \rVert \leq \big( m[{\boldsymbol{z}}(t_0)] E_\alpha(-\rho(t-t_0)^\alpha) \big)^b, \quad t>t_0 $$ 其中,
$ t_0 $ 为初始时刻,$\alpha \in (0, 1)$ ,$ \rho > 0 $ ,$ b>0 $ ,$m({\bf{0}}) = 0$ ,$ m({\boldsymbol{z}}) \geq 0 $ , 并且$ m({\boldsymbol{z}}) $ 在$ {\boldsymbol{z}} \in {{\bf{R}}^n} $ 上关于$ {\boldsymbol{z}} $ 满足局部Lipschitz条件, Lipschitz常数为$ m_0 $ ,$ E_\alpha $ 为Mittag-Leffler函数$$ E_\alpha(t) = \sum\limits_{k = 0}^\infty \frac{t^k}{\Gamma(k\alpha+1)}, \quad \forall \alpha>0, \; t \in {\bf{R}} $$ 注 1. Mittag-Leffler函数是指数函数的推广, 实际上,
$ E_1(t) = \exp(t) $ . 根据定义2, 当$ t\to\infty $ 时,$ E_\alpha(-\rho(t-t_0)^\alpha) \to 0 $ , 故一个Mittag-Leffler稳定的系统也是渐近稳定的, 从而也是Lyapunov稳定的. 因此, Mittag-Leffler稳定性也称为分数阶Lyapunov稳定性. Mittag-Leffler稳定性本质上是一种多项式稳定性[28].2. 基于状态反馈的反步控制器
为得到反馈控制的增益核函数, 首先简要回顾利用反步法针对系统(1) ~ (3)设计状态反馈的边界控制器的方法和主要结果.
考虑以下可逆反步积分变换
$$ {\boldsymbol{W}}(x,t) = {\boldsymbol{Z}}(x,t) + \int_0^x K(x,y) {\boldsymbol{Z}}(y,t) {{\,{\rm d}}y} $$ (4) 其中,
$ K(x,y) \in [L^2(0,1)]^{n \times n} $ 为控制增益核函数(矩阵),$ 0 \leq y \leq x \leq 1 $ . 利用积分变换(4)将系统(1) ~ (3)转换为以下目标系统$$ \begin{split} {_0^C D_t^\alpha}{\boldsymbol{W}}(x,t) =& A {\boldsymbol{W}}_{xx}(x,t) - C {\boldsymbol{W}}(x,t), \\ &\qquad\qquad\qquad\; (x,t) \in \Omega \end{split} $$ (5) $$ {\boldsymbol{W_x}}(0,t) = 0, \quad t>0\qquad\qquad\qquad\qquad $$ (6) $$ {\boldsymbol{W}}(1,t) = 0, \;\quad t>0\qquad\qquad\qquad\qquad$$ (7) 其中,
$ C \in {{\bf{R}}^{n \times n}} $ 为设计参数. 状态反馈控制器为$$ {\boldsymbol{U}}(t) = - \int_0^1 K(1,y) {\boldsymbol{Z}}(y,t) {{\,{\rm d}}y} $$ (8) 其中, 控制增益
$ K(1,y) = \left.K(x,y)\right|_{x = 1} $ . 利用文献[19, 26]类似的方法, 可以导出控制增益核函数矩阵$ K(x,y) $ 在$ 0 \leq y \leq x \leq 1 $ 上满足以下方程$$ \begin{split} K_{xx}(x,y) - K_{yy}(x,y) =\;& \dfrac{1}{a} \big( K(x,y) \Phi(y) +\\ & C K(x,y) \big) \end{split} $$ (9) $$ K(x,x) = -B + \frac{1}{2a} \int_0^x \big( \Phi(y) + C \big){\,\rm d}y\hspace{10pt} $$ (10) $$ K_y(x,0) = K(x,0) B\hspace{80pt} $$ (11) 推导过程与第3.1节类似, 此处略. 利用逐次逼近和数学归纳法[13, 17]可以证明方程(9) ~ (11)是适定的.
注 2. 若系统(1) ~ (3)耦合反应项系数
$ \Phi(x) = \Phi $ 为常数, 且$ B = 0 $ , 控制增益核函数$ K(x,y) = k(x,$ $y) I $ , 则令$ C = a c I - \Phi $ , 其中$ c>0 $ 为常数, 可将控制增益核函数方程(9) ~ (11)化为$ n $ 个相同的方程$$ \begin{split}& k_{xx}(x,y) - k_{yy}(x,y) = c k(x,y) \\ &k(x,x) = \dfrac{c}{2}x \\ & k_y(x,0) = 0 \end{split} $$ 根据文献[8]中定理10, 可知其解为
$$ \begin{split} k(x,y) = &\frac{-bc}{\sqrt{c+b^2}} \int_0^{x-y} {\rm e}^{-\frac{b\tau}{2}} \sinh\bigg( \frac{\sqrt{c+b^2}}{2}\tau \bigg) \times \\ & I_0\Big( \sqrt{c (x+y)(x-y-\tau)} \Big) {{\,{\rm d}}\tau}+ \\& c x \frac{I_1\Big( \sqrt{c(x^2-y^2)} \Big)}{\sqrt{c (x^2-y^2)}}\\[-20pt] \end{split} $$ (12) 其中,
$ I_n(\cdot) $ 为修正的$ n $ 阶Bessel函数.另外, 需要指出的是, 若
$ \Phi(x) $ 非常数矩阵或$ B\neq 0 $ , 要求得方程(9) ~ (11)的解析解是困难的. 对此, 本文将给出相应的数值解法.以下为叙述方便, 对任意
$ n $ 阶方阵$ X $ , 记$S[X] =$ $ (X+X^{{\rm T}})/2 $ 为$ X $ 的对称部分,$ \lambda(X) $ 为$ X $ 的所有特征值, 即$ X $ 的谱, 记$ \lambda_i(X) $ 为第$ i $ 个特征值,$i = 1, \cdots, n$ . 对$ n $ 阶实对称矩阵$ X $ ,$\lambda_{\min}(X) = \min_{1 \leq i \leq n} \lambda_i(X)$ 和$\lambda_{\max}(X) = \max_{1 \leq i \leq n} \lambda_i(X)$ 分别表示矩阵$ X $ 的最小和最大特征值.对于式(1) ~ (3)和式(8)组成的状态反馈控制闭环系统, 有以下结果:
定理1. 对任意初值
$ {\boldsymbol{Z}}(x,0) \in [L^2(0,1)]^n $ , 若矩阵$ C $ 满足$$ \lambda_{\min}(S[C]) > -\frac{\pi^2a}{4}$$ (13) 则系统(1) ~ (3)在
$ [L^2(0,1)]^n $ 空间上Mittag-Leffler稳定, 即存在不依赖于$ {\boldsymbol{Z}}(x,0) $ 的常数$ M>0 $ , 使得$$ \begin{split} &\lVert {\boldsymbol{Z}}(x,t) \rVert_{2,n} \leq \Big\{ M \Vert {\boldsymbol{Z}}(x,0) \rVert_{2,n}^2 \times \\ &\qquad E_\alpha\Big(-2\Big[\frac{\pi^2a}{4} + \lambda_{\min}(S[C])\Big] t^\alpha\Big) \Big\}^{\frac {1}{2}} \end{split} $$ (14) 其中, 控制器为式(8), 控制增益核函数矩阵
$ K(x,y) $ 由方程(9) ~ (11)确定.定理1的证明与定理4类似, 此处省略.
3. 观测器的设计
为了针对系统(1) ~ (3)设计观测器, 考虑以下估计系统
$$ \begin{split} & {_0^C D_t^\alpha}\widehat{{\boldsymbol{Z}}}(x,t) = A\widehat{{\boldsymbol{Z}}}_{xx}(x,t) + \Phi(x) \widehat{{\boldsymbol{Z}}}(x,t) + \\ & \qquad R_1(x) [ {\boldsymbol{Z}}(0,t)-\widehat{{\boldsymbol{Z}}}(0,t)], \quad (x,t) \in \Omega \end{split} $$ (15) $$ \begin{split} \widehat{{\boldsymbol{Z}}}_x(0,t) =\;& B {\boldsymbol{Z}}(0,t) + R_{10}[{\boldsymbol{Z}}(0,t) \; -\qquad\quad \\ & \widehat{{\boldsymbol{Z}}}(0,t)], \quad t>0 \end{split} $$ (16) $$ \widehat{{\boldsymbol{Z}}}(1,t) = {\boldsymbol{U}}(t), \quad t>0 \qquad\qquad\qquad\;\;\;\qquad$$ (17) 其中,
$ {n \times n} $ 矩阵$ R_1(x) $ 和$ R_{10} $ 为待设计的观测增益. 我们的目的是选择适当的观测增益$ R_1(x) $ 和$ R_{10} $ , 使得当$ t \to \infty $ 时, 观测器(15) ~ (17)中的系统状态估计$ \widehat{{\boldsymbol{Z}}}(x,t) $ 渐近收敛到系统(1) ~ (3)的状态$ {\boldsymbol{Z}}(x,t) $ .为此, 引入观测误差
$ \widetilde{{\boldsymbol{Z}}}(x,t) = {\boldsymbol{Z}}(x,t) - \widehat{{\boldsymbol{Z}}}(x,t) $ 表示系统真实状态$ {\boldsymbol{Z}}(x,t) $ 与估计状态$ \widehat{{\boldsymbol{Z}}}(x,t) $ 之差. 将系统(1) ~ (3)分别减观测器(15) ~ (17), 得误差系统$$ \begin{split} {_0^C D_t^\alpha}\widetilde{{\boldsymbol{Z}}}(x,t) =& A \widetilde{{\boldsymbol{Z}}}_{xx}(x,t) + \Phi(x) \widetilde{{\boldsymbol{Z}}}(x,t) - \\ & R_1(x) \widetilde{{\boldsymbol{Z}}}(0,t), \quad (x,t) \in \Omega \end{split} $$ (18) $$ \widetilde{{\boldsymbol{Z}}}_x(0,t) = -R_{10} \widetilde{{\boldsymbol{Z}}}(0,t), \quad t>0\; \qquad\qquad $$ (19) $$ \widetilde{{\boldsymbol{Z}}}(1,t) = 0, \quad t>0\qquad\qquad\qquad\qquad \;\quad\;$$ (20) 于是, 需要确定观测增益
$ R_1(x) $ 和$ R_{10} $ 使得当$ t\to\infty $ 时误差系统(18) ~ (20)收敛到平衡点$ \widetilde{{\boldsymbol{Z}}}(x,\cdot) = 0 $ . 为此, 利用以下反步积分变换$$ \widetilde{{\boldsymbol{Z}}}(x,t) = \widetilde{{\boldsymbol{W}}}(x,t) + \int_0^x R(x,y) \widetilde{{\boldsymbol{W}}}(y,t) {{\,{\rm d}}y} $$ (21) 将误差系统(18) ~ (20)转换为以下目标系统
$$ \begin{split} {_0^C D_t^\alpha}\widetilde{{\boldsymbol{W}}}(x,t) =& A\widetilde{{\boldsymbol{W}}}_{xx}(x,t) - \widetilde{C}\widetilde{{\boldsymbol{W}}}(x,t), \\& \qquad\qquad\qquad\; (x,t)\in\Omega \end{split} $$ (22) $$ \widetilde{{\boldsymbol{W}}}_x(0,t) = 0, \quad t>0 \qquad\qquad\qquad\qquad$$ (23) $$ \widetilde{{\boldsymbol{W}}}(1,t) = 0,\; \quad t>0 \qquad\qquad\qquad\qquad$$ (24) 其中, 矩阵
$ \widetilde{C}\in {{\bf{R}}^{n \times n}} $ 为待定参数. 适当选择参数$ \widetilde{C} $ 可使系统(22) ~ (24)稳定, 并且可以保证以一定的速率收敛到其平衡点$ \widetilde{{\boldsymbol{W}}}(x,\cdot) = 0 $ . 这也意味着观测器状态$ \widehat{{\boldsymbol{Z}}}(x,t) $ 收敛到系统的真实状态$ {\boldsymbol{Z}}(x,t) $ .3.1 确定核函数和观测增益
下面确定反步变换式(21)中的核函数矩阵
$ R(x,y) $ , 进而确定观测增益$ R_1(x) $ 和$ R_{10}. $ 命题 1. 若核函数
$ R(x,y) $ 满足方程$$ \begin{split} R_{xx}(x,y) - R_{yy}(x,y) =& -\frac{1}{a} \big( \Phi(x) R(x,y)\; + \\& R(x,y) \widetilde{C}\big) \end{split} $$ (25) $$ \frac{{\rm d}}{{{\rm d}}x}R(x,x) = -\frac{1}{2a}\Big(\Phi(x) + \widetilde{C}\Big) \qquad\qquad\quad\;\; $$ (26) $$ R(1,y) = 0\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\;$$ (27) 其中,
$ {n \times n} $ 矩阵$ \widetilde{C} $ 为设计参数,$ 0 \leq y \leq x \leq 1 $ , 则反步变换式(21)将观测器误差系统(18) ~ (20)变换为目标系统(22) ~ (24), 且观测增益分别为$$ R_1(x) = - a R_y(x,0) $$ (28) $$ R_{10} = - R(0,0)\qquad $$ (29) 证明. 利用Leibniz微分法则
$ \dfrac{{\rm d}}{{{\rm d}}x}\int_0^x f(x,y) {{\,{\rm d}}y} =$ $ f(x,x) + \int_0^x f_x(x,y) {{\,{\rm d}}y}, $ 并引入记号$\dfrac{{\rm d}}{{{\rm d}}x}R(x,x) = $ $R_x(x,y)|_{y = x} + R_y(x,y)|_{y = x} = R_x(x,x)\;+\;R_y(x,x)$ , 由变换式(21)对$ x $ 求导, 可得$$ \begin{split} \widetilde{{\boldsymbol{Z}}}_x(x,t) =\; &\widetilde{{\boldsymbol{W}}}_x(x,t) + R(x,x)\widetilde{{\boldsymbol{W}}}(x,t) \; + \qquad\;\\ & \int_0^x R_x(x,y) \widetilde{{\boldsymbol{W}}}(y,t) {{\,{\rm d}}y} \end{split} $$ (30) $$ \begin{split} \widetilde{{\boldsymbol{Z}}}_{xx}(x,t) =\;& \widetilde{{\boldsymbol{W}}}_{xx}(x,t) + \Big( \frac{{\rm d}}{{{\rm d}}x}R(x,x) \Big) \widetilde{{\boldsymbol{W}}}(x,t) \; + \\ & R(x,x)\widetilde{{\boldsymbol{W}}}_x(x,t) + R_x(x,x)\widetilde{{\boldsymbol{W}}}(x,t) \;+ \\ & \int_0^x R_{xx}(x,y) \widetilde{{\boldsymbol{W}}}(y,t) {{\,{\rm d}}y}\\[-17pt] \end{split} $$ (31) 沿系统(18)对变换式(21)求Caputo时间分数阶导数, 并应用分部积分和边界条件(23), 可得
$$ \begin{split} &{_0^C D_t^\alpha}\widetilde{{\boldsymbol{Z}}}(x,t) = A\widetilde{{\boldsymbol{W}}}_{xx}(x,t) - \widetilde{C}\widetilde{{\boldsymbol{W}}}(x,t) \; + \\ &\quad R(x,x)A\widetilde{{\boldsymbol{W}}}_x(x,t) - R_y(x,x)A\widetilde{{\boldsymbol{W}}}(x,t) \; + \\ &\quad R_y(x,0)A\widetilde{{\boldsymbol{W}}}(0,t) + \int_0^x R_{yy}(x,y)A\widetilde{{\boldsymbol{W}}}(y,t) {{\,{\rm d}}y} \; - \\ &\quad \int_0^x R(x,y)\widetilde{C}\widetilde{{\boldsymbol{W}}}(y,t) {{\,{\rm d}}y}\\[-17pt] \end{split} $$ (32) 将误差系统状态方程(18)两边减去式(32)并代入式(31), 同时考虑到
$ \widetilde{{\boldsymbol{Z}}}(0,t) = \widetilde{{\boldsymbol{W}}}(0,t) $ (对变换式(21)令$ x = 0 $ ), 可得$$ \begin{split} 0 =\;& \Big[ A \frac{{\rm d}}{{{\rm d}}x} R(x,x) + A R_x(x,x) + R_y(x,x)A \; + \\ & \Phi(x) + \widetilde{C}\Big] \widetilde{{\boldsymbol{W}}}(x,t) \; + \\ & \int_0^1 \Big[ A R_{xx}(x,y) - R_{yy}(x,y)A \; + \\ & \Phi(x) R(x,y) + R(x,y)\widetilde{C}\Big] \widetilde{{\boldsymbol{W}}}(y,t) {{\,{\rm d}}y} \; + \\ & \Big[ A R(x,x) - R(x,x)A \Big] \widetilde{{\boldsymbol{W}}}_x(x,t) \; -\\ & \Big[ R_1(x) + R_y(x,0)A \Big] \widetilde{{\boldsymbol{W}}}(0,t) \end{split} $$ (33) 显然, 要使方程(33)对所有
$ \widetilde{{\boldsymbol{W}}}(x,t) $ 成立, 核函数矩阵$ R(x,y) $ 应满足以下方程$$ \begin{split} & A R_{xx}(x,y) - R_{yy}(x,y) A + \Phi(x) R(x,y) \; +\, \\&\qquad R(x,y) \widetilde{C} = 0 \end{split} $$ (34) $$ \begin{split} & A \frac{\rm d}{{\rm d}x}R(x,x) + AR_x(x,x) + R_y(x,x) A \; +\quad \\ &\qquad \Phi(x) + \widetilde{C} = 0 \end{split} $$ (35) $$ R_1(x) + R_y(x,0)A = 0 \qquad\qquad\qquad\qquad $$ (36) $$ A R(x,x) - R(x,x) A = 0\qquad\qquad\qquad\quad$$ (37) 其中,
$ 0 \leq x \leq 1 $ ,$ 0 \leq y \leq x $ .再由变换式(21), 令
$ x = 1 $ , 可得$$ \widetilde{{\boldsymbol{Z}}}(1,t) = \widetilde{{\boldsymbol{W}}}(1,t) + \int_0^1 R(1,y) \widetilde{{\boldsymbol{W}}}(y,t) {{\,{\rm d}}y} $$ (38) 应用边界条件(20)和(24), 可知
$ R(1,y) = 0 $ . 最后, 代入$ A = aI $ , 可知核函数矩阵$ R(x,y) $ 满足方程(25) ~ (27).同时, 根据式(36)可知观测增益
$R_1(x) = -R_y(x,$ $ 0)A $ . 结合变换式(21)和式(30), 令$x = 0,$ 可得$$ \widetilde{{\boldsymbol{Z}}}(0,t) = \widetilde{{\boldsymbol{W}}}(0,t) \qquad\qquad\qquad\qquad\;\;$$ (39) $$ \widetilde{{\boldsymbol{Z}}}_x(0,t) = \widetilde{{\boldsymbol{W}}}_x(0,t) + R(0,0)\widetilde{{\boldsymbol{W}}}(0,t) $$ (40) 再利用边界条件式(19)和式(23)可知观测增益
$ R_{10} = $ $ - R(0,0) $ . □注 3. 若系统(1) ~ (3)耦合反应项系数
$ \Phi(x) = \Phi $ 为常数矩阵, 且观测器(15) ~ (17)的增益核函数$ R(x,y) = r(x,y)I $ , 则令$ \widetilde{C} = a \tilde{c}I - \Phi $ , 其中$ \tilde{c}>0 $ 为常数, 可将方程(25) ~ (27)化为$ n $ 个相同的方程$$ \begin{align} & r_{xx}(x,y) - r_{yy}(x,y) = - \tilde{c}r(x,y) \\& r(x,x) = \frac{\tilde{c}}{2}(1-x) \\& r(1,y) = 0 \end{align} $$ 其中,
$ 0 \leq y \leq x \leq 1 $ . 由文献[11]可知, 其解为$$ r(x,y) = \tilde{c}(1-x) \frac{I_1\Big( \sqrt{\tilde{c}(2-x-y)(x-y)} \Big)}{\sqrt{\tilde{c}(2-x-y)(x-y)}} $$ (41) $ 0 \leq y \leq x \leq 1 $ . 结合式(28)和式(29), 易得观测增益为$$ R_1(x) = \frac{a\tilde{c}(1-x)}{x(2-x)}I_2\Big( \sqrt{\tilde{c}x(2-x)} \Big) I $$ (42) $$ R_{10} = -\frac{\tilde{c}}{2} I \qquad\qquad\qquad\qquad\qquad\quad$$ (43) 其中,
$ I_n(\cdot) $ 为修正的$ n $ 阶Bessel函数.然而, 若
$ \Phi(x) $ 非常数矩阵, 则难以求得方程(25) ~ (27)的解析解. 对此本文将给出其数值解.关于核函数矩阵方程(25) ~ (27)的适定性, 有以下结论.
定理2. 核函数矩阵方程(25) ~ (27)在
$0 \leq y \leq $ $ x \leq 1 $ 上有唯一解, 且二阶连续可微.证明. 首先, 利用变量替换
$ \bar x = 1-y $ ,$ \bar y = 1-x $ , 令$ \bar R(\bar x, \bar y) = R(x,y) $ , 将方程(25) ~ (27)转化为$$ \begin{split} {\bar R}_{{\bar x}{\bar x}}({\bar x},{\bar y}) - {\bar R}_{{\bar y}{\bar y}}({\bar x},{\bar y}) =& \frac{1}{a} \big( \Phi(1-{\bar y}) {\bar R}({\bar x},{\bar y}) + \\ & {\bar R}({\bar x},{\bar y})\widetilde{C}\big) \end{split} $$ (44) $$ {\bar R}_{\bar y}({\bar x},{\bar x}) = \frac{1}{2a} \big( \Phi(1-{\bar x}) + \widetilde{C}\big)\qquad\qquad\qquad$$ (45) $$ {\bar R}({\bar x},0) = 0 \qquad\qquad\qquad\qquad\qquad \qquad\qquad$$ (46) 其中,
$ 0 \leq {\bar y}\leq {\bar x}\leq 1 $ . 再次引入变量替换$ \xi = {\bar x}+{\bar y} $ ,$ \eta = {\bar x}-{\bar y} $ , 令$ G(\xi,\eta) = {\bar R}({\bar x},{\bar y}) $ , 将方程(44) ~ (46)转化为方程$$ G_{\xi\eta}(\xi,\eta) = \frac{1}{4a} \Big[ \Phi\Big(1-\frac{\xi-\eta}{2}\Big) G(\xi,\eta) + G(\xi,\eta)\widetilde{C}\Big] $$ (47) $$ G_\xi(\xi,0) = \frac{1}{2a} \Big[ \Phi\Big(1-\frac{\xi}{2}\Big) + \widetilde{C}\Big] \qquad\qquad\qquad\quad $$ (48) $$ G(\xi,\xi) = 0 \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad$$ (49) 其中,
$ \quad 0 \leq \eta \leq \xi \leq 2 $ . 利用文献[14]中定理3, 可知方程(47) ~ (49)的解是有界的. 与文献[8]类似,采用逐次逼近法容易证明方程(47) ~ (49)的解存在且唯一, 并且该解是二次连续可微的.再根据上述变换中方程的等价性, 可知结论成立. □3.2 误差系统的稳定性
下面先考虑目标系统(22) ~ (24)的稳定性, 再讨论误差系统(18) ~ (20)的稳定性. 为证明目标系统的稳定性, 先给出一个重要引理.
引理1[34]. 若
$ z(t) \in {\bf{R}} $ 是连续且可微函数, 对任意时刻$ t \geq t_0 \geq 0 $ , 有$$ \frac{1}{2} {_0^C D_t^\alpha}z^2(t) \leq z(t) {_0^C D_t^\alpha}z(t), \quad 0 < \alpha < 1. $$ 对目标系统(22) ~ (24), 有以下结论:
定理3. 对任意初值
$ \widetilde{{\boldsymbol{W}}}(x,0) \in [L^2(0,1)]^n $ , 若矩阵$ \widetilde{C} $ 满足$$ \lambda_{\min}(S[\widetilde{C}]) > -\frac{\pi^2a}{4} $$ (50) 则系统(22) ~ (24)在
$ [L^2(0,1)]^n $ 空间上Mittag-Leffler稳定$$ \begin{split} &\lVert \widetilde{{\boldsymbol{W}}}(x,t) \rVert_{2,n} \leq \Big\{ \Vert \widetilde{{\boldsymbol{W}}}(x,0) \rVert_{2,n}^2 \times \\ &\qquad E_\alpha\Big(-2\Big[\frac{\pi^2a}{4} + \lambda_{\min}(S[\widetilde{C}])\Big] t^\alpha\Big) \Big\}^{\frac{1}{2}} \end{split} $$ (51) 证明. 由定义1可知,
$ \widetilde{{\boldsymbol{W}}}(x,\cdot) = 0 $ 是目标系统(22) ~ (24)的平衡点. 取Lyapunov函数$$ V_1(t) = \frac{1}{2} \int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) \widetilde{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} $$ (52) 沿系统(22)对
$ V_1(t) $ 求Caputo时间分数阶导数, 并应用引理1, 得$$ \begin{split} {_0^C D_t^\alpha}V_1(t) \leq\;& \int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) {_0^C D_t^\alpha}\widetilde{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} = \\ & \int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) A \widetilde{{\boldsymbol{W}}}_{xx}(x,t) {{\,{\rm d}}x} \;- \\ & \int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) \widetilde{C}\widetilde{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} \end{split} $$ (53) 应用分部积分及边界条件(23)和(24), 将式(53)第1项改写为
$$ \begin{split} &\int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) A \widetilde{{\boldsymbol{W}}}_{xx}(x,t) {{\,{\rm d}}x} = \\ & \qquad- \int_0^1 \widetilde{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) A \widetilde{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x} \end{split} $$ (54) 将式(54)代入式(53), 并应用Wirtinger不等式[12, 31], 即
$ \displaystyle\int_0^1 \big( w_i(x,t) - w_i(1,t) \big)^2 {{\,{\rm d}}x} \leq \dfrac{4}{\pi^2} \displaystyle\int_0^1 w_{ix}^2(x,t) {{\,{\rm d}}x}, $ 其中,$ w_i(1,t) = 0, $ $ i = 1,\cdots,n, $ 可得$$ {_0^C D_t^\alpha}V_1(t) \leq - 2 \Big[ \frac{\pi^2a}{4} + \lambda_{\min}(S[\widetilde{C}]) \Big] V_1(t) $$ (55) 因为
$\lambda_{\min}(S[\widetilde{C}]) > -{\pi^2a}/{4}$ , 应用分数阶Lyapunov方法[29], 可得$$ V_1(t) \leq V_1(0) E_\alpha\Big(-2\Big[\frac{\pi^2a}{4} + \lambda_{\min}(S[\widetilde{C}])\Big] t^\alpha\Big)$$ (56) 根据定义2以及
$ V_1(t) = \dfrac{1}{2} \lVert \widetilde{{\boldsymbol{W}}}(x,t) \rVert_{2,n}^2 $ , 式(51)成立. □注 4. 定理3可以看作对文献[15]中定理3的推广, 由于证明过程中应用了Wirtinger不等式[12, 31]而非Poincaré不等式, 所以得到的条件式(50)更加宽松, 不等式右端从
$ -a/4 $ 降至$ -\pi^2 a/4 $ , 进一步扩大了设计参数$ \widetilde{C} $ 的选择范围.另外, 根据文献[28]中引理2.1, 定理3的结果式(51)可具有更紧的形式:
$$ \begin{split} &\lVert \widetilde{{\boldsymbol{W}}}(x,t) \rVert_{2,n}^2\leq \lVert \widetilde{{\boldsymbol{W}}}(x,0) \rVert_{2,n}^2 \times \\ &\qquad E_\alpha^2\Big(-\Big[ \frac{\pi^2a}{4} + \lambda_{\min}(S[ \widetilde{C}]) \Big]t^\alpha\Big) \end{split} $$ 但这并不影响定理条件式(50).
下面说明变换式(21)是可逆的. 假设其逆变换为
$$ \widetilde{{\boldsymbol{W}}}(x,t) = \widetilde{{\boldsymbol{Z}}}(x,t) - \int_0^x L(x,y) \widetilde{{\boldsymbol{Z}}}(y,t) {{\,{\rm d}}y} $$ (57) 则核函数
$ L(x,y) $ 满足方程$$ \begin{split} L_{xx}(x,y) - L_{yy}(x,y) =& \frac{1}{a}\Big[L(x,y)\big( \Phi(y)+R_1(y) \big) + \\ & \widetilde{C}L(x,y) \Big] \\[-15pt]\end{split} $$ (58) $$ \frac{{\rm d}}{{{\rm d}}x}L(x,x) = -\frac{1}{2a}\big( \Phi(x) + \widetilde{C}\big) \qquad\qquad\qquad\quad$$ (59) $$ L_y(x,0) = - L(x,0)AR_{10} - R_1(x)\qquad\qquad\quad$$ (60) 运用定理2证明类似的方法, 可以证明
$ L(x,y) $ 在$ 0 \leq y \leq x \leq 1 $ 上的解存在唯一, 且二阶连续可微.于是, 结合定理2和变换式(21)的可逆性, 由文献[7]可知核函数方程(25) ~ (27)的解
$ R(x,y) $ 定义了一个有界线性算子[35]$ \mathcal{K} \colon [L^2(0,1)]^n \to [L^2(0,1)]^n $ , 即$ (\mathcal{K}\widetilde{{\boldsymbol{W}}})(x,t) = \widetilde{{\boldsymbol{Z}}}(x,t) $ . 同时, 算子$ \mathcal{K} $ 的代数逆$ \mathcal{K}^{-1} \colon [L^2(0,1)]^n \to [L^2(0,1)]^n $ 也是一个有界线性算子, 且由核函数$ L(x,y) $ 以及变换式(57)确定. 因此, 必存在不依赖于$ \widetilde{{\boldsymbol{{Z}}}}(x,0) $ 和$ \widetilde{{\boldsymbol{{W}}}}(x,0) $ 的常数$ \beta>0 $ 和$ \gamma>0 $ , 使得$$ \lVert \widetilde{{\boldsymbol{Z}}}(x,t) \rVert_{2,n} \leq \beta \lVert \widetilde{{\boldsymbol{W}}}(x,t) \rVert_{2,n}, \quad t \geq 0 $$ (61) $$ \lVert \widetilde{{\boldsymbol{W}}}(x,t) \rVert_{2,n} \leq \gamma \lVert \widetilde{{\boldsymbol{Z}}}(x,t) \rVert_{2,n}, \quad t \geq 0 $$ (62) 下面, 给出误差系统(18) ~ (20)的稳定性结果.
定理 4. 对任意初值
$ \widetilde{{\boldsymbol{Z}}}(x,0) \in [L^2(0,1)]^n $ 以及观测增益(28)和(29), 若矩阵$ \widetilde{C} $ 满足$$ \lambda_{\min}(S[\widetilde{C}]) > -\frac{\pi^2a}{4} $$ (63) 则系统(18) ~ (20)在
$ [L^2(0,1)]^n $ 空间上Mittag-Leffler稳定, 即存在不依赖于$ \widetilde{{\boldsymbol{Z}}}(x,0) $ 的常数$ M>0 $ , 使得$$ \begin{split} &\lVert \widetilde{{\boldsymbol{Z}}}(x,t) \rVert_{2,n} \leq \Big\{ M \Vert \widetilde{{\boldsymbol{Z}}}(x,0) \rVert_{2,n}^2 \times \\ &\qquad E_\alpha\Big(-2\Big[\frac{\pi^2a}{4} + \lambda_{\min}(S[\widetilde{C}])\Big] t^\alpha\Big) \Big\}^{\frac{1}{2}} \end{split} $$ (64) 证明. 结合命题1和定理3, 应用不等式(61)和(62), 定理结论式(64)不难证明, 此处略. □
注 5. 定理4表明, 适当选择设计参数
$ \widetilde{C} $ , 当$ t\to\infty $ 时, 观测器误差$ \widetilde{{\boldsymbol{Z}}}(x,t) \to 0 $ , 即观测器的估计状态$ \widehat{{\boldsymbol{Z}}}(x,t) $ 收敛到系统状态$ {\boldsymbol{Z}}(x,t) $ . 进一步地, 从式(64)还可以看出, 只要改变$ \widetilde{C} $ 的最小特征值$ \lambda_{\min}(S[\widetilde{C}]) $ , 就可以调节误差系统$ \widetilde{{\boldsymbol{Z}}}(x,t) $ 的收敛速度. 实际上, 若令$ \widetilde{C} = \tilde{c}I $ , 只要$\tilde{c} > -{\pi^2a}/{4}$ , 即可保证观测器$ \widehat{{\boldsymbol{Z}}}(x,t) $ 收敛到系统状态$ {\boldsymbol{Z}}(x,t) $ (当$ t \to \infty $ 时).4. 基于观测器的输出反馈控制器
为设计基于观测器的输出反馈控制器, 考虑可逆的反步积分变换
$$ \widehat{{\boldsymbol{W}}}(x,t) = \widehat{{\boldsymbol{Z}}}(x,t) + \int_0^x K(x,y) \widehat{{\boldsymbol{Z}}}(y,t) {{\,{\rm d}}y} $$ (65) 其中,
$ n $ 阶方阵$ K(x,y) $ 为方程(9) ~ (11)确定的控制增益核函数(矩阵). 利用反步变换式(65)将观测器(15) ~ (17)变换为以下目标系统$$ \begin{split} & {_0^C D_t^\alpha}\widehat{{\boldsymbol{W}}}(x,t) = A \widehat{{\boldsymbol{W}}}_{xx}(x,t) - C \widehat{{\boldsymbol{W}}}(x,t) + \bigg[ R_1(x) + \\ &\qquad \int_0^x K(x,y) R_1(y) {{\,{\rm d}}y}\bigg] \widetilde{{\boldsymbol{W}}}(0,t),\;\;(x,t) \in \Omega \\[-18pt]\end{split} $$ (66) $$ \widehat{{\boldsymbol{W}}}_x(0,t) = B \widehat{{\boldsymbol{W}}}(0,t) + (B+R_{10})\widetilde{{\boldsymbol{W}}}(0,t),\;\; t>0 $$ (67) $$ \widehat{{\boldsymbol{W}}}(1,t) = 0, \quad t>0\qquad\qquad\qquad\qquad\qquad\quad$$ (68) 其中,
$ R_1(x) $ 和$ R_{10} $ 分别为式(28)和式(29)确定的观测增益,$ n $ 阶方阵$ C $ 为设计参数. 根据边界条件式(17)和式(68), 令$ x = 1 $ , 由变换式(65), 可得控制器为$$ {\boldsymbol{U}}(t) = - \int_0^1 K(1,y) \widehat{{\boldsymbol{Z}}}(y,t) {{\,{\rm d}}y} $$ (69) 其中,
$ K(1,y) = \left.K(x,y)\right|_{x = 1} $ 为控制增益.下面给出本文的主要结果. 为叙述简便, 以下用
$ \big({\boldsymbol{Z}}(x,t), \widehat{{\boldsymbol{Z}}}(x,t) \big) $ 简记联合系统状态$ \big[{\boldsymbol{Z}}(x,t)^{{\rm T}},$ $ \widehat{{\boldsymbol{Z}}}(x,t)^{{\rm T}}\big]^{{\rm T}} \in [L^2(0,1)]^{2n} $ .定理5. 对任意初值
$ \big( {\boldsymbol{Z}}( x,0 ), \widehat{{\boldsymbol{Z}}}( x,0 ) \big) \in [L^2( 0,1 )]^{2n} $ , 若矩阵$ C $ 和$ \widetilde{C} $ 满足$$ \min \big\{ \lambda_{\min}(S[\widetilde{C}]), \lambda_{\min}(S[C]) \big\} > -\frac{\pi^2a}{8} $$ (70) 那么系统(1) ~ (3)与观测器(15) ~ (17)以及控制器(69)组成的联合闭环系统在
$ [L^2(0,1)]^{2n} $ 空间上Mittag-Leffler稳定, 即存在不依赖于$ \big({\boldsymbol{Z}}(x,0), \widehat{{\boldsymbol{Z}}}(x,0) \big) $ 的常数$M > 0 ,$ 使得$$ \begin{split} &\big\lVert \big( {\boldsymbol{Z}}(x,t), \widehat{{\boldsymbol{Z}}}(x,t) \big) \big\rVert_{2,2n} \leq \\ &\qquad\Big\{ M \big\lVert \big( {\boldsymbol{Z}}(x,0), \widehat{{\boldsymbol{Z}}}(x,0) \big) \big\rVert_{2,2n}^2 E_\alpha\Big( -2 \Big[ \frac{\pi^2a}{8} \;\; + \\ &\qquad \min \big\{ \lambda_{\min}(S[\widetilde{C}]), \lambda_{\min}(S[C]) \big\} \Big] t^\alpha \Big) \Big\}^{\frac{1}{2}} \\[-15pt]\end{split} $$ (71) 其中, 控制增益
$ K(1,y) = \left.K(x,y)\right|_{x = 1} $ 由方程(9) ~ (11)确定, 观测增益分别由式(28)和式(29)给出.证明. 因为由系统(1) ~ (3)、观测器(15) ~ (17)及控制器(69)组成的闭环联合系统
$ \big({\boldsymbol{Z}}(x,t), \widehat{{\boldsymbol{Z}}}(x,t) \big) $ 等价于由观测器(15) ~ (17)和误差系统(18) ~ (20)以及控制器(69)组成的联合系统$ \big(\widehat{{\boldsymbol{Z}}}(x,t), \widetilde{{\boldsymbol{Z}}}(x,t)\big) $ , 进一步应用可逆反步变换式(65)和式(21)可变换为联合目标系统$ \big(\widehat{{\boldsymbol{W}}}(x,t), \widetilde{{\boldsymbol{W}}}(x,t)\big) $ , 即系统(66) ~ (68)和(22) ~ (24).首先证明联合目标系统
$ \big(\widehat{{\boldsymbol{W}}}(x,t), \widetilde{{\boldsymbol{W}}}(x,t)\big) $ 的稳定性. 考虑以下Lyapunov函数$$ \begin{split} V_2(t) =\;& \frac{F}{2}\int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) \widetilde{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} \;+ \\ & \frac{1}{2} \int_0^1 \widehat{{\boldsymbol{W}}}^{{\rm T}}(x,t) \widehat{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} \end{split} $$ (72) 其中,
$ F $ 为待定系数. 应用引理1, 沿系统(66)和(22)对式(72)求Caputo时间分数阶导数, 得$$ \begin{split} {_0^C D_t^\alpha}V_2(t) \leq \;&F \int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) {_0^C D_t^\alpha}\widetilde{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} \; +\\ & F \int_0^1 \widehat{{\boldsymbol{W}}}^{{\rm T}}(x,t){_0^C D_t^\alpha}\widehat{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} = \\ & F \int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) A \widetilde{{\boldsymbol{W}}}_{xx}(x,t) {{\,{\rm d}}x} \; - \\ & F \int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) \widetilde{C}\widetilde{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} \; + \\ & \int_0^1 \widehat{{\boldsymbol{W}}}^{{\rm T}}(x,t) A \widehat{{\boldsymbol{W}}}_{xx}(x,t) {{\,{\rm d}}x} \; - \\ & \int_0^1 \widehat{{\boldsymbol{W}}}^{{\rm T}}(x,t) C \widehat{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} \; + \\ & \int_0^1 \widehat{{\boldsymbol{W}}}^{{\rm T}}(x,t) H(x) \widetilde{{\boldsymbol{W}}}(0,t) {{\,{\rm d}}x} \end{split} $$ (73) 其中,
$ H(x) = R_1(x) + \int_0^x K(x,y) R_1(y) {{\,{\rm d}}y} $ .应用分部积分和边界条件式(23)及式(24), 可得
$$ \begin{split}& \int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) A \widetilde{{\boldsymbol{W}}}_{xx}(x,t) {{\,{\rm d}}x} = \\ & \qquad - \int_0^1 \widetilde{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) A \widetilde{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x} \end{split} $$ (74) 类似地, 应用分部积分和边界条件式(67), 式(68), 可得
$$ \begin{split} &\int_0^1 \widehat{{\boldsymbol{W}}}^{{\rm T}}(x,t) A \widehat{{\boldsymbol{W}}}_{xx}(x,t) {{\,{\rm d}}x} = \\[-3pt] & \qquad - \widehat{{\boldsymbol{W}}}^{{\rm T}}(0,t) A B \widehat{{\boldsymbol{W}}}(0,t) - \widehat{{\boldsymbol{W}}}^{{\rm T}}(0,t) A (B + R_{10}) \times \\[-3pt] &\qquad\quad \widetilde{{\boldsymbol{W}}}(0,t) - \int_0^1 \widehat{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) A \widehat{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x} \\[-18pt]\end{split} $$ (75) 将式(74)和(75)代入式(73), 得到
$$ \begin{split} & {_0^C D_t^\alpha}V_2(t) \leq - F \int_0^1 \widetilde{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) A \widetilde{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x} \; - \\ & \qquad F \int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) \widetilde{C}\widetilde{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} - \widehat{{\boldsymbol{W}}}^{{\rm T}}(0,t) A B \; \times \\ & \qquad \widehat{{\boldsymbol{W}}}(0,t) - \widehat{{\boldsymbol{W}}}^{{\rm T}}(0,t) A (B+R_{10})\widetilde{{\boldsymbol{W}}}(0,t) \; - \\ & \qquad\int_0^1 \widehat{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) A \widehat{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x}- \int_0^1 \widehat{{\boldsymbol{W}}}^{{\rm T}}(x,t) C \; \times \\ &\qquad \widehat{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} + \int_0^1 \widehat{{\boldsymbol{W}}}^{{\rm T}}(x,t) H(x) \widetilde{{\boldsymbol{W}}}(0,t) {{\,{\rm d}}x} \\[-18pt] \end{split} $$ (76) 利用Young不等式, 并结合边界条件式(24)和式(68), 应用Cauchy-Schwarz不等式, 可得
$$ \begin{split} - \widehat{{\boldsymbol{W}}}^{{\rm T}}&(0,t) A (B+R_{10})\widetilde{{\boldsymbol{W}}}(0,t) \leq \\ &\frac{a}{4} \widehat{{\boldsymbol{W}}}^{{\rm T}}(0,t) \widehat{{\boldsymbol{W}}}(0,t) + \frac{\lambda_{M1}^2}{a} \widetilde{{\boldsymbol{W}}}^{{\rm T}}(0,t)\widetilde{{\boldsymbol{W}}}(0,t) = \\ & \frac{a}{4}\int_0^1 \widehat{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) {{\,{\rm d}}x}\int_0^1 \widehat{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x} \; + \\ & \frac{\lambda_{M1}^2}{a} \int_0^1 \widetilde{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) {{\,{\rm d}}x}\int_0^1 \widetilde{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x} \leq \\ &\frac{a}{4}\int_0^1 \widehat{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) \widehat{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x}\; + \\ & \frac{\lambda_{M1}^2}{a} \int_0^1 \widetilde{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) \widetilde{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x}\\[-18pt] \end{split} $$ (77) 其中,
$\lambda_{M1}^2 = \lVert A(B+R_{10}) \rVert_2^2 = \lambda_{\max}([A(B+R_{10})]^ {{\rm T}}\times$ $ [A(B+ R_{10})])$ . 应用Young不等式和Poincaré不等式, 可得$$ \begin{split} &\int_0^1 \widehat{{\boldsymbol{W}}}^{{\rm T}}(x,t) H(x) \widetilde{{\boldsymbol{W}}}(0,t) {{\,{\rm d}}x} \leq \\& \qquad\frac{a}{4} \int_0^1 \widehat{{\boldsymbol{W}}}_x^{{\rm T}}(x,t)\widehat{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x}+ \\& \qquad\frac{\lambda_{M2}^2}{a} \int_0^1 \widetilde{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) \widetilde{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x} \end{split} $$ (78) 其中,
$$ \begin{split} &\lambda_{M2}^2 = \sup_{0 \leq x \leq 1} \lVert H(x) \rVert_2^2 = \sup_{0 \leq x \leq 1} \lambda_{\max}(H(x)^ {{\rm T}}H(x))\end{split} $$ 将式(77)和式(78)代入式(76)右端, 可得
$$ \begin{split} & {_0^C D_t^\alpha}V_2(t) \leq - \bigg( Fa - \frac{\lambda_{M1}^2}{a} - \frac{\lambda_{M2}^2}{a} \bigg) \int_0^1 \widetilde{{\boldsymbol{W}}}_x^{{\rm T}}(x,t) \times\\&\qquad \widetilde{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x} - \frac{a}{2} \int_0^1 \widehat{{\boldsymbol{W}}}_x^{{\rm T}}(x,t)\widehat{{\boldsymbol{W}}}_x(x,t) {{\,{\rm d}}x} - \\&\qquad F \lambda_{\min}(S[\widetilde{C}]) \int_0^1 \widetilde{{\boldsymbol{W}}}^{{\rm T}}(x,t) \widetilde{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x}- \\&\qquad \lambda_{\min}(S[C]) \int_0^1 \widehat{{\boldsymbol{W}}}^{{\rm T}}(x,t) \widehat{{\boldsymbol{W}}}(x,t) {{\,{\rm d}}x} \\[-18pt] \end{split} $$ (79) 令
$ F = 2(\lambda_{M1}^2 + \lambda_{M2}^2)/a^2, $ 可使$Fa - \lambda_{M1}^2/a - $ $\lambda_{M2}^2/a = Fa/2 > 0 $ . 利用边界条件式(24)和式(68), 并应用Wirtinger不等式, 可得$$ {_0^C D_t^\alpha}V_2(t) \leq - 2 \Big[\frac{\pi^2a}{8} + \lambda_0 \Big] V_2(t) $$ 其中,
$\lambda_0 = \min\big\{ \lambda_{\min}(S[\widetilde{C}]), \lambda_{\min}(S[C]) \big\}$ . 结合定理条件(70), 利用分数阶Lyapunov方法, 可知$$ V_2(t) \leq V_2(0) E_\alpha\Big(- 2 \Big[\frac{\pi^2a}{8} + \lambda_0 \Big] t^\alpha\Big) $$ (80) 根据式(72)和范数
$ \lVert\,\cdot\,\rVert_{2,2n} $ 的定义, 必有$$ \begin{split} &\beta_1 \big\lVert \big(\widehat{{\boldsymbol{W}}}(x,t), \widetilde{{\boldsymbol{W}}}(x,t)\big) \big\rVert_{2,2n}^2 \leq V_2(t) \leq \\ & \qquad\gamma_1 \big\lVert \big(\widehat{{\boldsymbol{W}}}(x,t), \widetilde{{\boldsymbol{W}}}(x,t)\big) \big\rVert_{2,2n}^2 \end{split} $$ (81) 其中,
$ \beta_1>0 $ 和$ \gamma_1>0 $ 为不依赖于$ \big(\widehat{{\boldsymbol{W}}}(x,0), \widetilde{{\boldsymbol{W}}}(x,0)\big) $ 的常数. 结合式(80)和式(81)以及定理条件式(70), 可得$$ \begin{split}& \big\lVert \big(\widehat{{\boldsymbol{W}}}(t), \widetilde{{\boldsymbol{W}}}(t)\big) \big\rVert_{2,2n}^2 \leq \frac{\gamma_1}{\beta_1} \big\lVert \big(\widehat{{\boldsymbol{W}}}(0), \widetilde{{\boldsymbol{W}}}(0)\big) \big\rVert_{2,2n}^2 \nonumber\times \\&\qquad E_\alpha\Big(- 2 \Big[\frac{\pi^2a}{8} + \lambda_0 \Big] t^\alpha\Big) \end{split} $$ 其中,
$ \widehat{{\boldsymbol{W}}}(t) = \widehat{{\boldsymbol{W}}}(x,t) $ ,$ \widetilde{{\boldsymbol{W}}}(t) = \widetilde{{\boldsymbol{W}}}(x,t) $ . 因此, 联合目标系统状态$ \big(\widehat{{\boldsymbol{W}}}(x,t), \widetilde{{\boldsymbol{W}}}(x,t)\big) $ 是Mittag-Leffler稳定的.又因为变换式(21)和式(65)都是可逆的, 故联合系统
$ \big(\widehat{{\boldsymbol{Z}}}(x,t), \widetilde{{\boldsymbol{Z}}}(x,t)\big) $ 状态也是Mittag-Leffler稳定的, 即存在不依赖于$ \big(\widehat{{\boldsymbol{Z}}}(x,0), \widetilde{{\boldsymbol{Z}}}(x,0)\big) $ 的常数$ M_1>0 $ , 使得$$ \begin{split} & \big\lVert \big(\widehat{{\boldsymbol{Z}}}(t), \widetilde{{\boldsymbol{Z}}}(t)\big) \big\rVert_{2,2n} \leq \Big\{ M_1 \big\lVert \big(\widehat{{\boldsymbol{Z}}}(0), \widetilde{{\boldsymbol{Z}}}(0)\big) \big\rVert_{2,2n}^2 \times\\& \qquad E_\alpha\Big(- 2 \Big[\frac{\pi^2a}{8} + \lambda_0 \Big] t^\alpha\Big) \Big\}^{\frac{1}{2}} \end{split} $$ 其中,
$ \widehat{{\boldsymbol{Z}}}(t) = \widehat{{\boldsymbol{Z}}}(x,t) $ ,$ \widetilde{{\boldsymbol{Z}}}(t) = \widetilde{{\boldsymbol{Z}}}(x,t) $ .最后, 因为
$ {\boldsymbol{Z}}(x,t) = \widehat{{\boldsymbol{Z}}}(x,t) + \widetilde{{\boldsymbol{Z}}}(x,t) $ , 所以联合系统$ \big({\boldsymbol{Z}}(x,t), \widehat{{\boldsymbol{Z}}}(x,t) \big) $ 也是Mittag-Leffler稳定的, 式(71)成立. □注 6. 定理5中的条件比文献[15]中定理4的条件保守性更小. 一方面, 证明过程应用了Wirtinger不等式, 所得定理条件的下界更小. 另一方面, 证明过程中对
$ \lambda_{\min}(S[\widetilde{C}]) $ 和$ \lambda_{\min}(S[C]) $ 的大小关系未做任何假设.从定理4和定理5的结论可以看出, 设计参数
$ \widetilde{C} $ 和$ C $ 直接决定了观测增益核函数$ R(x,y) $ 和控制增益核函数$ K(x,y) $ , 从而决定了观测器和输出反馈控制器的设计. 另外, 若要得到核函数的解析解, 则需对参数施加其他约束[21]. 反之, 若利用核函数的数值解, 则可以更加灵活地选取设计参数. 在实际应用中, 可根据需要采取适当的策略. 下面针对两种典型情况, 给出两个算法实现基于观测器的输出反馈控制设计. 该算法将用于第5节的数值仿真.算法 1 (
${\boldsymbol{\Phi(x) }}$ 为常数矩阵). 对耦合分数阶反应扩散系统(1) ~ (3), 若耦合反应项系数矩阵$ \Phi(x)= $ $\Phi $ 为常数矩阵, 且边界条件式(2)满足$ B=0 $ , 则令$ \widetilde{C}= \tilde{c}a I - \Phi $ ,$ C = c a I - \Phi $ , 选取参数$ \tilde{c} $ 和$ c $ 满足条件$$ \min \{ \tilde{c}, c \} > \max \Big\{ \frac{1}{a} \lambda_{\max}(S[\Phi]) - \frac{\pi^2}{8}, 0 \Big\} $$ (82) 利用式(42)和式(43)求得观测器(15) ~ (17)的增益矩阵
$ R_1(x) $ 和$ R_{10} $ . 由式(12)得到控制增益核函数(矩阵)$ K(1,y) = k(1,y)I $ .对满足条件式(82)的矩阵
$ \widetilde{C} $ 和$ C $ , 其特征值满足$ \lambda_{\min}(S[\widetilde{C}]) = \tilde{c}a - \lambda_{\max}(S[\Phi]) $ ,$ \lambda_{\min}(S[C]) = c a -$ $ \lambda_{\max}(S[\Phi]) $ . 根据定理5条件式(70), 可知$\min \{\tilde{c}, c \} > $ $\dfrac{1}{a}\lambda_{\max}(S[\Phi]) - {\pi^2}/{8}$ . 另外, 解式(42)要求$ \tilde{c}>0 $ , 解式(12)要求$ c>0 $ . 综上可知, 满足条件式(82)的$ \tilde{c} $ 和$ c $ 可使参数矩阵$ \widetilde{C} $ 和$ C $ 同时满足定理条件式(63), (13)和式(70).算法 2 (
${\boldsymbol{\Phi(x)}}$ 为非常数矩阵). 对于耦合反应项系数$ \Phi(x) $ 为非常数的耦合分数阶反应扩散系统(1) ~ (3), 选取矩阵$ \widetilde{C}= \tilde{c}a I $ 和$ C = c a I $ , 令参数$ \tilde{c} $ 和$ c $ 满足$$ \min \{\tilde{c}, c \} > -\frac{\pi^2}{8} $$ (83) 数值求解核函数矩阵方程(25) ~ (27)和(9) ~ (11), 分别得到观测增益(28)和(29)以及控制增益
$ K(1,y) $ . 具体的数值解法将在第5节给出.显然, 上述算法中矩阵
$ \widetilde{C} $ 和$ C $ 的特征值分别为$ \tilde{c}a $ 和$ c a $ , 满足条件式(83)的矩阵$ \widetilde{C} $ 和$ C $ 同时满足定理4、 定理1和定理5的条件.5. 数值仿真
为了验证本文的理论结果, 下面给出两个数值仿真例子. 利用文献[36]提出的Caputo分数阶扩散方程数值解法, 针对耦合分数阶反应扩散系统(1) ~ (3)和观测器(15) ~ (17)及控制器(69)组成的闭环系统, 采用有限差分方法在空间域和时间域上离散化. 这里将空间域
$ [0,L] $ 和时间域$ [0,T] $ 分别均匀划分为$ N $ 和$ Q $ 个区间, 其中$ L = 1 $ ,$ N = 100 $ ,$ T = 5 $ ,$ Q = 500 $ .当
$ \Phi(x) $ 为非常数矩阵时, 难以求得核函数$ K(x,y) $ 和$ R(x,y) $ 的解析解, 可采用数值方法求解对应的核函数方程(9) ~ (11)和(25) ~ (27). 下面将文献[8]中提出的核函数方程数值解法推广到耦合系统, 分别给出相应核函数方程的数值解法. 首先对空间$ 0 \leq y \leq x \leq 1 $ 离散化, 令$ h = 1/N $ ,$ x_i = (i-1)h $ ,$ i = 1,\cdots, N+1 $ ,$ y_j = (j-1)h $ ,$ j = 1,\cdots,i $ . 对控制增益核函数$ K(x,y) $ , 记$ K^{ij} = K(x_i,y_j) \in {{\bf{R}}^{n \times n}} $ ,$ \Phi^i = \Phi(x_i) $ , 则有以下数值解:$$ \begin{align} & K^{i+1,j} = 2\widehat K^{ij} + \frac{h^2}{a} \big(\widehat K^{ij} \Phi^j + C \widehat K^{ij} \big) - K^{i-1,j} \\& K^{i+1,i+1} = K^{ii} + \frac{h}{4a}\big( \Phi^{i+1} + \Phi^{i} + 2C \big) \\& {{{\boldsymbol{V}}_K^{i+1,1}}} = \bigg[(1+bh)I + \frac{bh^3}{2a}Q\bigg]^{-1} \Bigg[ \bigg(I+\frac{h^2}{2a}Q\bigg)\times \\&\qquad\qquad \bigg(2 {{{\boldsymbol{V}}_K^{i,2}}} - bh{{{\boldsymbol{V}}_K^{i-1,1}}}\bigg) - {{{\boldsymbol{V}}_K^{i-1,1}}} \Bigg] \end{align} $$ 其中,
$ \widehat K^{ij} = ( K^{i,j+1} + K^{i,j-1} ) / 2 $ ,$ {{{\boldsymbol{V}}_K^{ij}}} \in {\bf{R}}^{n^2} $ 表示矩阵$ K^{ij} $ 的列拉直(列展开),$ n^2\times n^2 $ 矩阵$Q = {\Phi^1}^{\rm T} \oplus C$ , 其中$ \oplus $ 表示矩阵的Kronecker和(Kronecker sum), 或者等价地,$Q = {\Phi^1}^{\rm T}\otimes I_{n\times n} +$ $ I_{n\times n} \otimes C $ , 这里$ \otimes $ 表示矩阵的Kronecker积(Kronecker product). 分别求解$ K^{i+1,j} $ ,$ K^{i+1,i+1} $ 和$ K^{i+1,1} $ ,$i = 1,\cdots,N+ 1$ ,$ j = 1,\cdots,i $ , 即可得到控制增益核函数$ K(x,y) $ 的数值解. 对观测增益核函数$ R(x,y) $ , 记$R^{ij} = R(x_i,y_j) \in {{\bf{R}}^{n \times n}}$ ,$ \Phi^i = \Phi(x_i) $ , 可采用以下数值解格式求解$$ \begin{align} & R^{i,j-1} = 2 \widehat R^{ij} + \frac{h^2}{a}\big( \Phi^i \widehat R^{ij} + \widehat R^{ij} \widetilde{C} \big) - R^{i,j+1} \\ & R^{ii} = R^{i+1,i+1} + \frac{h}{4a}\big( \Phi^{i+1} + \Phi^i + 2 \widetilde{C} \big) \\ & R^{N+1,j} = 0 \end{align} $$ 其中,
$ \widehat R^{ij} = (R^{i+1,j}+R^{i-1,j})/2 $ ,$ i = N+1,\cdots, 1 $ ,$ j = i,\cdots,1 $ .仿真 1. 考虑
$ n = 2 $ 的耦合分数阶反应扩散系统(1) ~ (3), 其中$ \alpha = 0.7 $ ,$ a = 1 $ ,$ b = 0 $ , 耦合反应项系数$\Phi(x) = \Phi = \left[ {\begin{aligned}1\;\;2\\3\;\;4\end{aligned}} \right]$ 为常数矩阵. 系统初值为$z_{1}(x,0) \;=\; 3\;+\;3x(1-x)\sin(4\pi x)$ ,$z_2(x,0) \;= \;\pi+$ $\cos(6\pi x) $ . 该系统在开环条件下($ {\boldsymbol{U}}(t) = 0 $ )是不稳定的. 从图2(a)可以看出, 开环系统状态$ L^2 $ 范数发散.
图 2 开环和闭环系统的状态$ L^2 $ 范数Fig. 2 The state$ L^2 $ norm of open-loop and close-loop systems利用算法1, 选取控制参数
$ \tilde{c} = 5 $ ,$ c = 4.5 $ , 满足$\min\{\tilde{c}, c\} > \lambda_{\max}(S[\Phi]) - {\pi^2}/{8} = 4.1818$ , 其中$\lambda_{\max}(S[\Phi]) $ $ = 5.4155 $ , 可以得到观测增益$ R_1(x) = R_1^{11}(x)I $ (图3(a))和控制增益核函数$ K(1,y) $ (图3(b)). 采用基于观测器的输出反馈控制(69), 得到控制输入如图3(c)所示. 图2(b)给出了系统$ {\boldsymbol{Z}}(x,t) $ 及观测器系统$ \widehat{{\boldsymbol{Z}}}(x,t) $ 和误差系统$ \widetilde{{\boldsymbol{Z}}}(x,t) $ 的$ L^2 $ 范数. 可以看到, 随着误差$ \widetilde{{\boldsymbol{Z}}}(x,t) $ 逐渐收敛到$ 0 $ , 观测器$ \widehat{{\boldsymbol{Z}}}(x,t) $ 收敛到系统状态$ {\boldsymbol{Z}}(x,t) $ . 图4展示了两个系统状态分量的演化过程. 可以看出系统状态Mittag-Leffler稳定到平衡点$ {\boldsymbol{Z}}(x,t) = 0 $ .
图 3 观测增益, 控制增益核函数和控制输入Fig. 3 The observer gain and control gain kernel functions, and control input为验证受控系统对测量噪声的鲁棒性, 对边界测量输出
$ {\boldsymbol{Y}}(t) = {\boldsymbol{Z}}(0,t) $ 添加信噪比为$ 25 $ dB的白噪声信号, 图5给出了系统的控制输入以及系统状态$ L^2 $ 范数和状态演化. 从图5(b) ~ 5(d)可以看出, 在有测量噪声的情况下, 受控系统和观测器误差系统状态均鲁棒地收敛到$ 0 $ , 说明本文提出的基于观测器的输出反馈控制方法对测量噪声具有较好的鲁棒性.仿真 2. 考虑由3个
$(n = 3)$ 分数阶反应扩散过程组成的耦合系统(1) ~ (3), 其中$ \alpha = 0.7 $ ,$ a = 1 $ ,$ b = 1 $ , 空间依赖的耦合反应项系数$ \Phi(x) $ 为$$ \begin{align} \begin{bmatrix} 2+\sin(2\pi x) & 2+\cos(2\pi x) & 1+x(1-x) \\ 3+(x-{\dfrac{1}{2}})^2 & 2+\cos(2\pi x) & 1+x(1-x) \\ 2+\sin(2\pi x) & 3+(x-\dfrac{1}{2})^2 & 2+\cos(2\pi x) \end{bmatrix} \end{align} $$ 系统初值为
$ z_1(x,0) = 3 + 3x(1 - x)\sin(4\pi x) $ ,$z_2(x,0) = $ $ \pi + \cos(6\pi x) $ ,$ z_3(x,0) =\pi + \exp(x) \sin(8\pi x) $ . 该系统在开环条件下($ u_1(t) = u_2(t) = u_3(t) = 0 $ )是不稳定的. 如图6(a)所示, 开环系统状态范数$ \lVert {\boldsymbol{Z}}(\cdot,t) \rVert_{2,n} $ 是发散的.
图 6 开环和闭环系统的状态$ L^2 $ 范数Fig. 6 The state$ L^2 $ norm of open-loop and close-loop systems应用算法2, 选取参数
$ \tilde{c} = c = 1 $ , 即参数矩阵$\widetilde C = C = \left[ {\begin{aligned}1\;\;0\\0\;\;1\end{aligned}} \right]$ (满足定理5条件). 利用数值方法求解观测增益核函数(25) ~ (27), 得到观测增益$ R_1(x) $ (图7(a))和
图 7 观测增益, 控制增益核函数和控制输入Fig. 7 The observer gain and control gain kernel functions, and control input$$\begin{align} R_{10} = \begin{bmatrix} -1.5 & -1.0 & -0.5833 \\ -1.5417 & -1.5 & -0.5833 \\ -1.0 & -1.5417 & -1.5 \end{bmatrix} \end{align}$$ 同时, 数值求解控制增益核函数矩阵PDE (9) ~ (11)得
$ K(1,y) = K(x,y)|_{x = 1} $ (图7(b)). 利用式(69)得到基于观测器的边界控制输入${\boldsymbol{U}}(t)$ (图7(c)).图6(b)给出了闭环系统、观测器和误差系统的状态范数. 可以看出误差系统的
$ L^2 $ 范数收敛到$ 0 $ , 说明了观测器(15) ~ (17)的有效性. 图8(a) ~ 8(c)给出了闭环系统各状态分量的时空演化过程. 可见闭环系统的状态$ L^2 $ 范数收敛到$ 0 $ , 这说明基于观测器的边界控制式(69)使耦合系统(1) ~ (3) Mittag-Leffler 稳定.最后, 图9对比了不同控制参数下系统的状态范数, 可以看出随着控制参数
$ \tilde c $ 和$ c $ 增大, 受控系统的收敛速度变得更快.
图 9 不同控制参数下闭环系统的状态$ L^2 $ 范数Fig. 9 State$ \tilde{c} $ -norm of close-loop systems under different control parameters6. 结束语
本文针对具有空间依赖耦合系数的时间分数阶反应扩散系统, 利用PDEs反步法提出了一种边界测量、边界控制的输出反馈控制器, 选择适当的设计参数, 可使闭环系统以一定的收敛速率Mittag-Leffler稳定. 首先, 基于边界测量输出设计了系统观测器, 选择适当的观测器参数, 可根据观测增益核函数矩阵PDE求得观测增益, 并且可保证观测器的状态估计以一定的速率收敛到系统真实状态. 然后, 进一步利用PDEs反步法提出了基于观测器的边界输出反馈控制器, 选择合适的控制器参数, 可根据控制增益核函数矩阵PDE求得控制增益, 且保证闭环系统以一定的速率Mittag-Leffler稳定到平衡点. 同时, 进一步扩大了观测器和控制器设计参数的选择范围.
本文分析了观测增益和控制增益核函数矩阵方程解的存在唯一性, 并且针对耦合系数为常数矩阵的情况, 在假设核函数矩阵为数量阵的条件下, 可以求得两个核函数的解析解. 但当耦合系数矩阵随空间变化时, 通常无法求得解析解. 为此, 本文给出了控制增益和观测增益核函数矩阵的数值解, 无需预先假设核函数矩阵的结构, 即可直接求得矩阵中n2个核函数, 使得设计参数矩阵的选择更加简便和灵活. 数值仿真验证了本文提出方法的有效性.
-
图 2 开环和闭环系统的状态
$ L^2 $ 范数Fig. 2 The state
$ L^2 $ norm of open-loop and close-loop systems
图 3 观测增益, 控制增益核函数和控制输入
Fig. 3 The observer gain and control gain kernel functions, and control input
图 6 开环和闭环系统的状态
$ L^2 $ 范数Fig. 6 The state
$ L^2 $ norm of open-loop and close-loop systems
图 7 观测增益, 控制增益核函数和控制输入
Fig. 7 The observer gain and control gain kernel functions, and control input
-
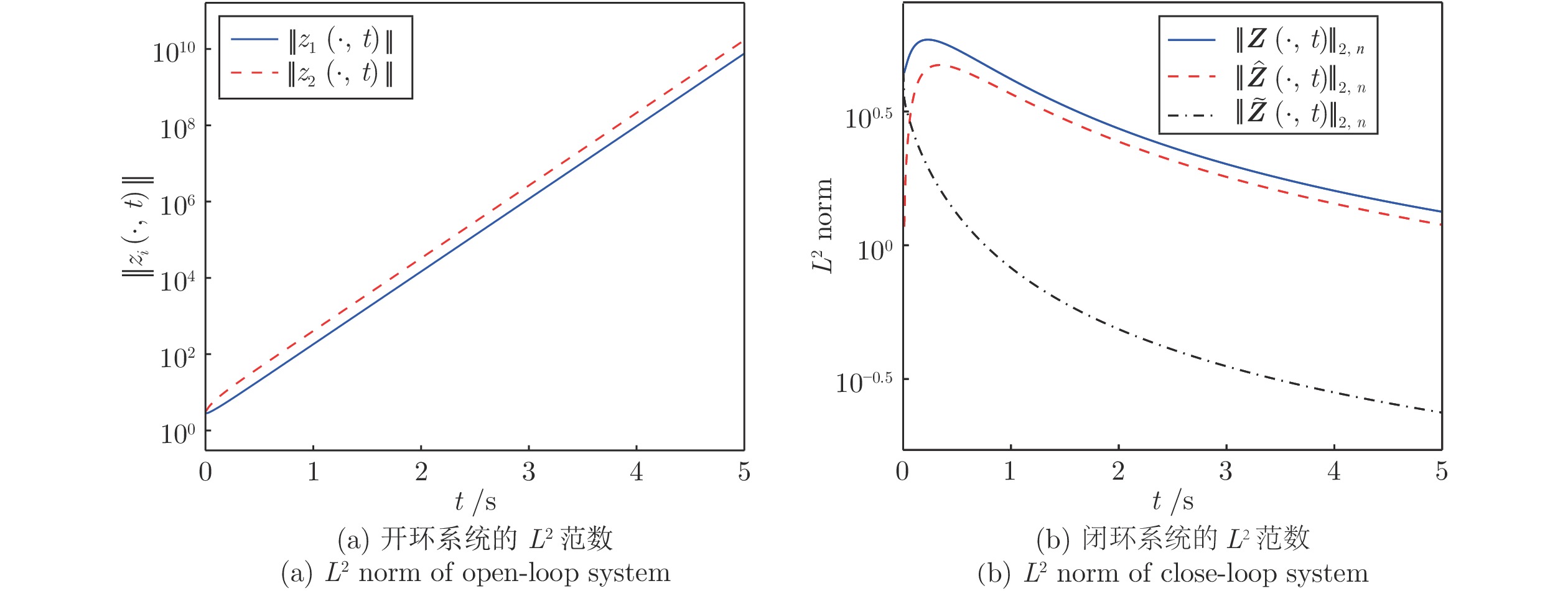
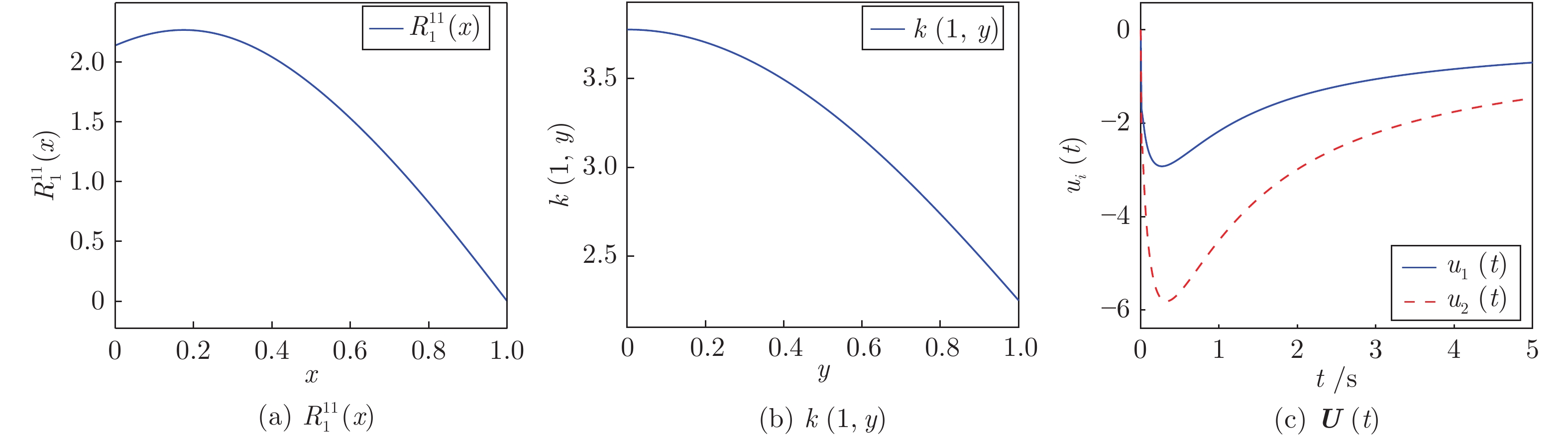
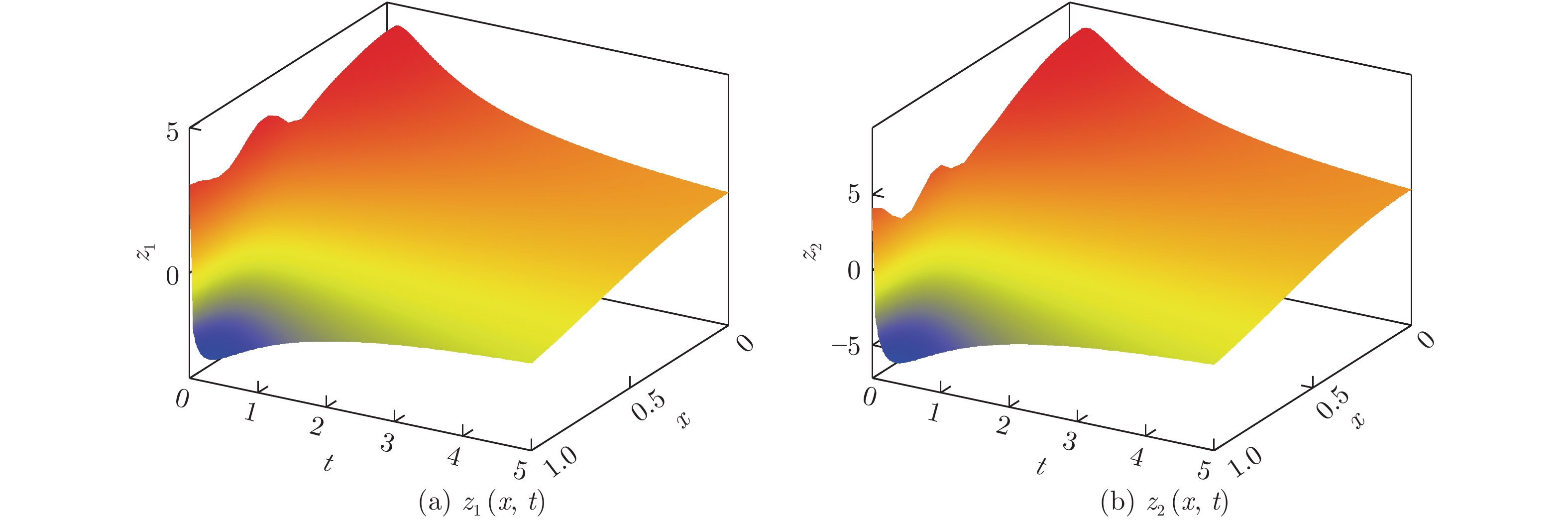
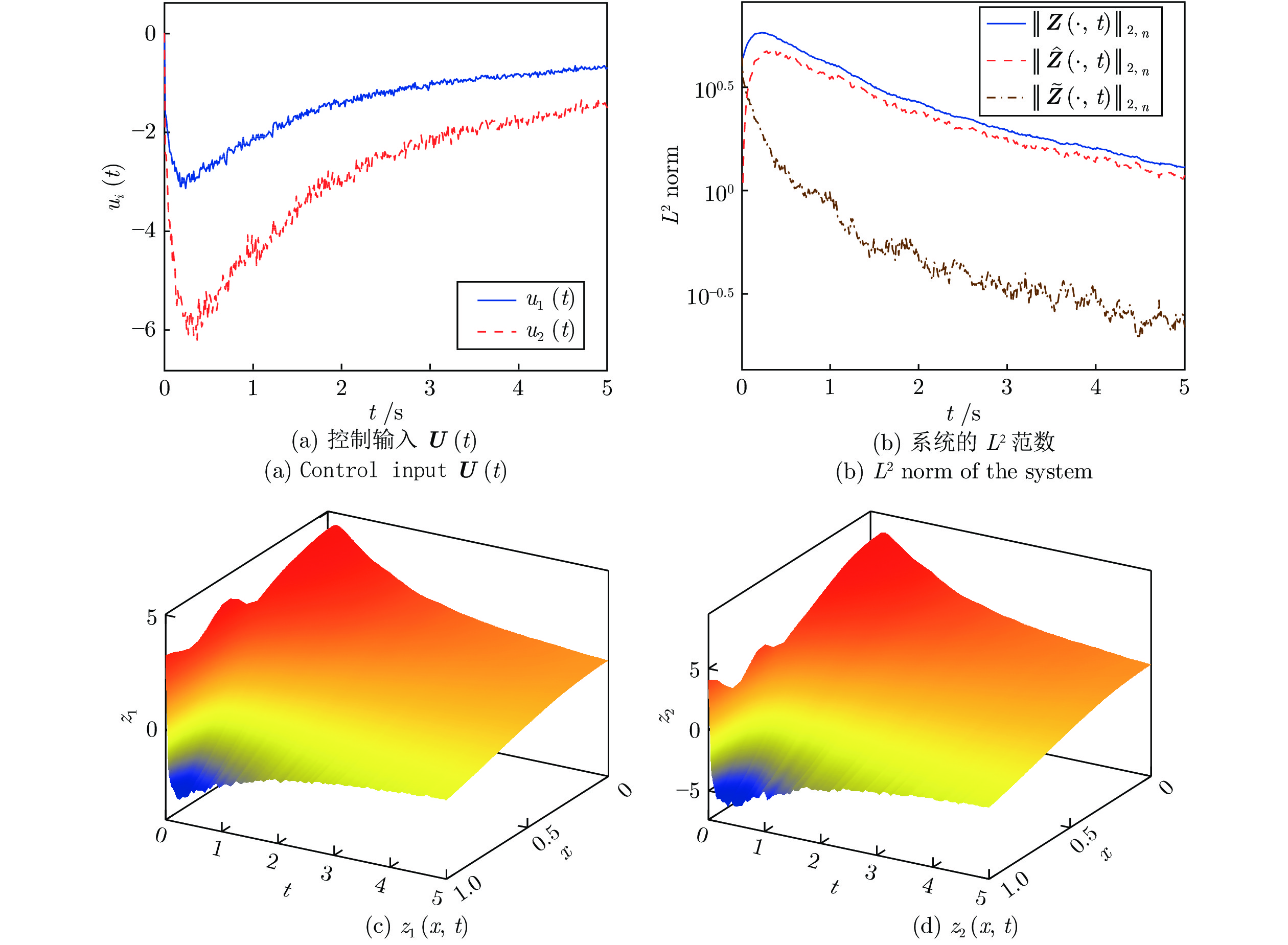
[1] Saxena R K, Mathai A M, Haubold H J. Fractional reactiondiffusion equations. Astrophysics and Space Science, 2006, 305(3):289-296 doi: 10.1007/s10509-006-9189-6 [2] Henry B I, Langlands T A M, Wearne S L. Anomalous diffusion with linear reaction dynamics: From continuous time random walks to fractional reaction-diffusion equations. Physical Review E, 2006, 74(3):031116 doi: 10.1103/PhysRevE.74.031116 [3] Podlubny I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and some of Their Applications. New York: Academic Press, 1999. [4] del Castillo-Negrete D, Carreras B A, Lynch V E. Front dynamics in reaction-diffusion systems with Levy flights: a fractional diffusion approach. Physical Review Letters, 2003, 91:018302 doi: 10.1103/PhysRevLett.91.018302 [5] 张桂梅, 孙晓旭, 刘建新, 储珺. 基于分数阶微分的TV-L1光流模型的图像配准方法研究. 自动化学报, 2017, 43(12):2213-2224Zhang Gui-Mei, Sun Xxiao-Xu, Liu Jian-Xin, Chu Jun. Research on TV-L1 optical flow model for image registration based on fractional-order differentiation. Acta Automatica Sinica, 2017, 43(12):2213-2224 [6] Yin H W, Wen X Q. Pattern formation through temporal fractional derivatives. Scientific Reports, 2018, 8(1):5070 doi: 10.1038/s41598-018-23470-8 [7] Liu W J. Boundary feedback stabilization of an unstable heat equation. SIAM Journal on Control & Optimization, 2003, 42(3):1033-1043 [8] Smyshlyaev A, Krstic M. Closed-form boundary state feedbacks for a class of 1-D partial integro-differential equations. IEEE Transactions on Automatic Control, 2004, 49(12): 2185-2202 doi: 10.1109/TAC.2004.838495 [9] Smyshlyaev A, Krstic M. Backstepping observers for a class of parabolic PDEs. Systems & Control Letters, 2005, 54(7): 613-625 [10] Smyshlyaev A, Krstic M. On control design for PDEs with space-dependent diffusivity or time-dependent reactivity. Automatica, 2005, 41(9):1601-1608 doi: 10.1016/j.automatica.2005.04.006 [11] Krstic B M, Smyshlyaev A. Boundary Control of PDEs: A Course on Backstepping Design. Philadelphia: Society for Industrial and Applied Mathematics, 2008. [12] Smyshlyaev A. Adaptive Control of Parabolic PDEs. Princeton: Princeton University Press, 2010. [13] Baccoli A, Pisano A, Orlov Y. Boundary control of coupled reaction-diffusion processes with constant parameters. Automatica, 2015, 54:80-90 doi: 10.1016/j.automatica.2015.01.032 [14] Baccoli A, Pisano A. Anticollocated backstepping observer design for a class of coupled reaction-diffusion PDEs. Journal of Control Science and Engineering, 2015, 2015:1-10 [15] Liu B N, Boutat D, Liu D Y. Backstepping observer-based output feedback control for a class of coupled parabolic PDEs with different diffusions. Systems & Control Letters, 2016, 97:61-69 [16] Orlov Y, Pisano A, Pilloni A, Usia E. Output feedback stabilization of coupled reaction-diffusion processes with constant parameters. SIAM Journal on Control and Optimization, 2017, 55(6):4112-4155 doi: 10.1137/15M1034325 [17] Vazquez R, Krstic M. Boundary control of coupled reactionadvection-diffusion systems with spatially-varying coefficients. IEEE Transactions on Automatic Control, 2017, 62(4):2026-2033 doi: 10.1109/TAC.2016.2590506 [18] Deutscher J, Kerschbaum S. Output regulation for coupled linear parabolic PIDEs. Automatica, 2019, 100:360-370 doi: 10.1016/j.automatica.2018.11.033 [19] Ge F D, Chen Y Q, Kou C H. Boundary feedback stabilisation for the time fractional-order anomalous diffusion system. IET Control Theory & Applications, 2016, 10(11):1250-1257 [20] Ge F D, Chen Y Q. Extended Luenberger-type observer for a class of semilinear time fractional diffusion systems. Chaos, Solitons & Fractals, 2017, 102:229-235 [21] Ge F D, Meurer T, Chen Y. Mittag-Leffler convergent backstepping observers for coupled semilinear subdiffusion systems with spatially varying parameters. Systems & Control Letters, 2018, 122:86-92 [22] Ge F D, Chen Y Q. Observer design for semilinear time fractional diffusion systems with spatially varying parameters. In: Proceedings of the 2018 International Conference on Fractional Differentiation and Its Applications. Amman, Jordan: SSRN, 2018. [Online], available: http://dx.doi.org/10.2139/ssrn.3281639 [23] Ge F D, Chen Y Q. Event-triggered boundary feedback control for networked reaction-subdiffusion processes with input uncertainties. Information Sciences, 2019, 476:239-255. doi: 10.1016/j.ins.2018.10.023 [24] Chen J, Zhuang B, Chen Y Q, Cui B T. Backstepping-based boundary feedback control for a fractional reaction diffusion system with mixed or Robin boundary conditions. IET Control Theory & Applications, 2017, 11(17):2964-2976. [25] Chen J, Cui B T, Chen Y Q, Mao L. Backstepping-based observer for output feedback stabilization of a boundary controlled fractional reaction diffusion system. In: Proceedings of the 11th Asian Control Conference. Gold Coast, Australia: IEEE, 2017. 2435−2440 [26] Chen J, Cui B T, Chen Y Q. Backstepping-based boundary control design for a fractional reaction diffusion system with a space-dependent diffusion coefficient. ISA Transactions, 2018, 80:203-211 doi: 10.1016/j.isatra.2018.04.013 [27] Chen J, Cui B T, Chen Y Q. Observer-based output feedback control for a boundary controlled fractional reaction diffusion system with spatially-varying diffusivity. IET Control Theory & Applications, 2018, 12(11):1561-1572 [28] Zhou H C, Guo B Z. Boundary feedback stabilization for an unstable time fractional reaction diffusion equation. SIAM Journal on Control and Optimization, 2018, 56(1):75-101 doi: 10.1137/15M1048999 [29] Li Y, Chen Y Q, Podlubny I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica, 2009, 45(8):1965-1969 doi: 10.1016/j.automatica.2009.04.003 [30] Li Y, Chen Y Q, Podlubny I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Computers & Mathematics with Applications, 2010, 59(5):1810-1821 [31] Hardy G H, Littlewood J E, Pólya G. Inequalities. 2nd ed. Cambridge, UK: Cambridge University Press, 1988. [32] Podlubny I. Fractional-order systems and PIλDµ-controllers. IEEE Transactions on Automatic Control, 1999, 44(1):208-214 doi: 10.1109/9.739144 [33] Matignon D. Stability results for fractional differential equations with applications to control processing. Computational Engineering in Systems Applications, 1996, 2:963-968 [34] Aguila-Camacho N, Duarte-Mermoud M A, Gallegos J A. Lyapunov functions for fractional order systems. Communications in Nonlinear Science & Numerical Simulation, 2014, 19(9):2951-2957 [35] Curtain R F, Zwart H. An Introduction to Infinitedimensional Linear Systems Theory. New York: Springer Science and Business Media, 1995. [36] Li H F, Cao J X, Li C P. High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (III). Journal of Computational and Applied Mathematics, 2016, 299:159-175 doi: 10.1016/j.cam.2015.11.037 期刊类型引用(1)
1. 董顺科，肖敏，虞文武. Schnakenberg系统的时空斑图演化机理研究. 自动化学报. 2024(08): 1620-1630 . 
本站查看其他类型引用(4)
-
下载:
下载:
计量
- 文章访问数: 572
- HTML全文浏览量: 142
- PDF下载量: 222
- 被引次数: 5
