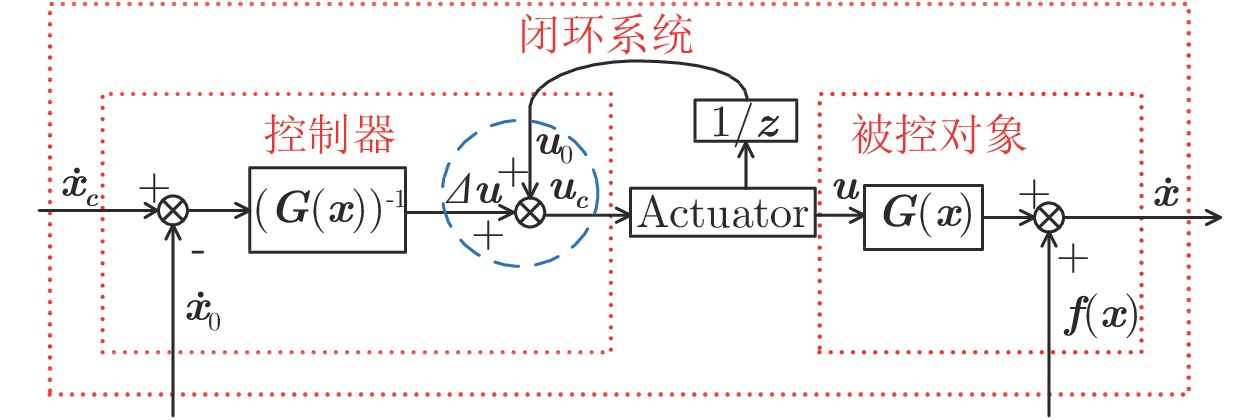
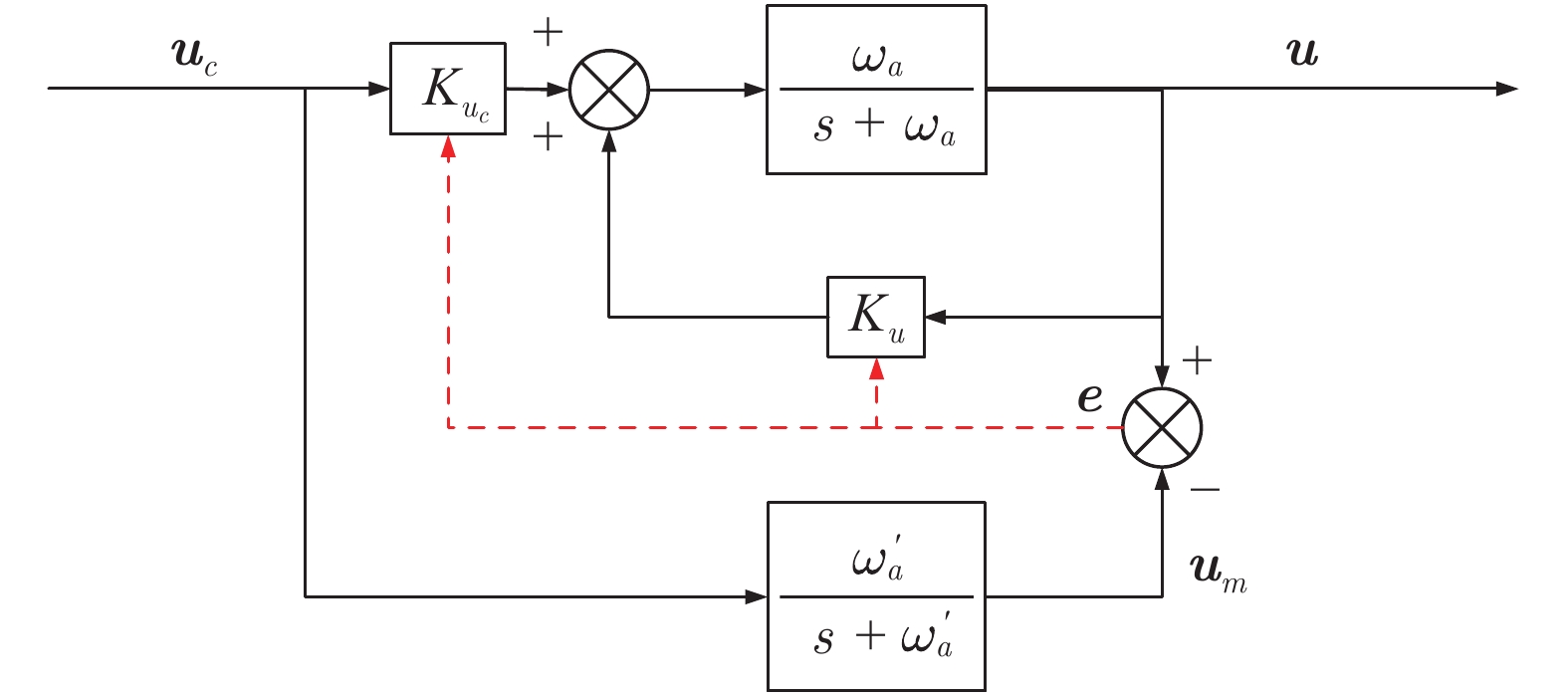
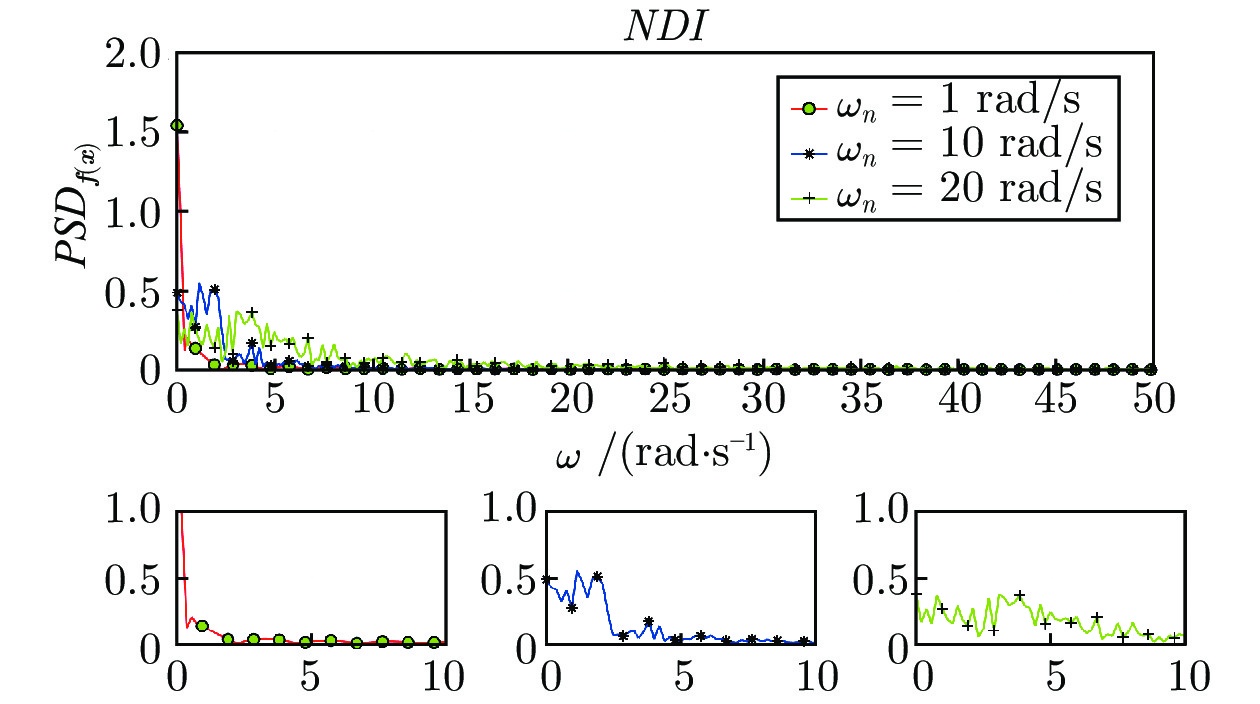
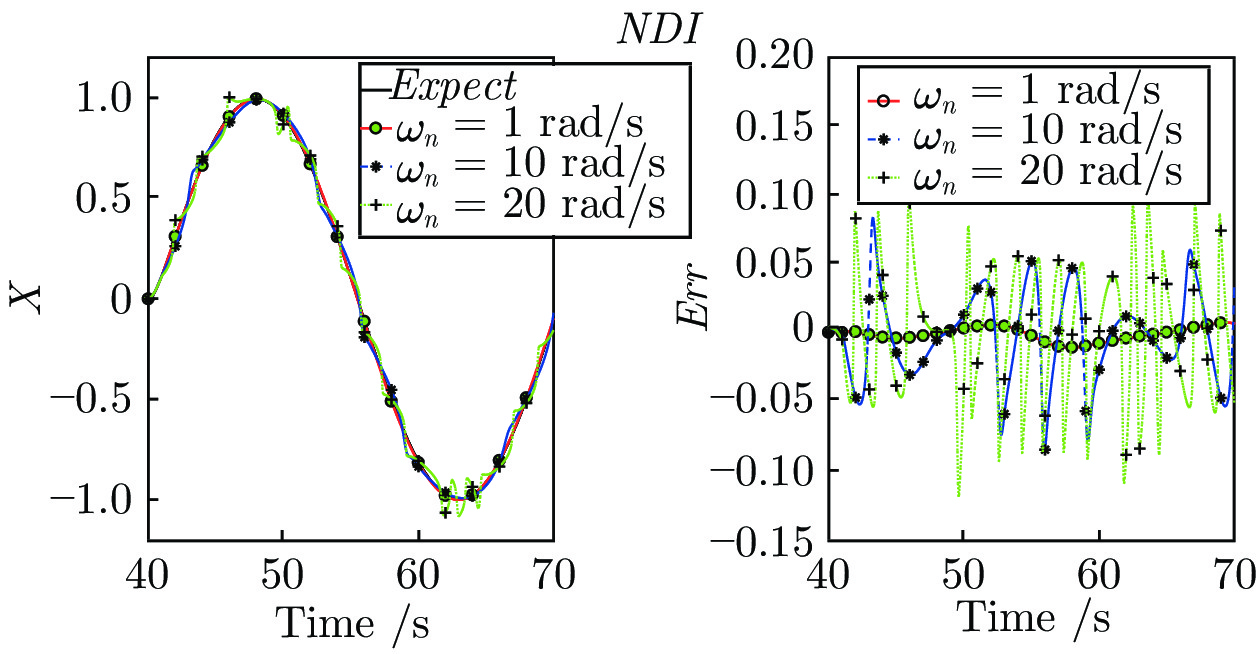
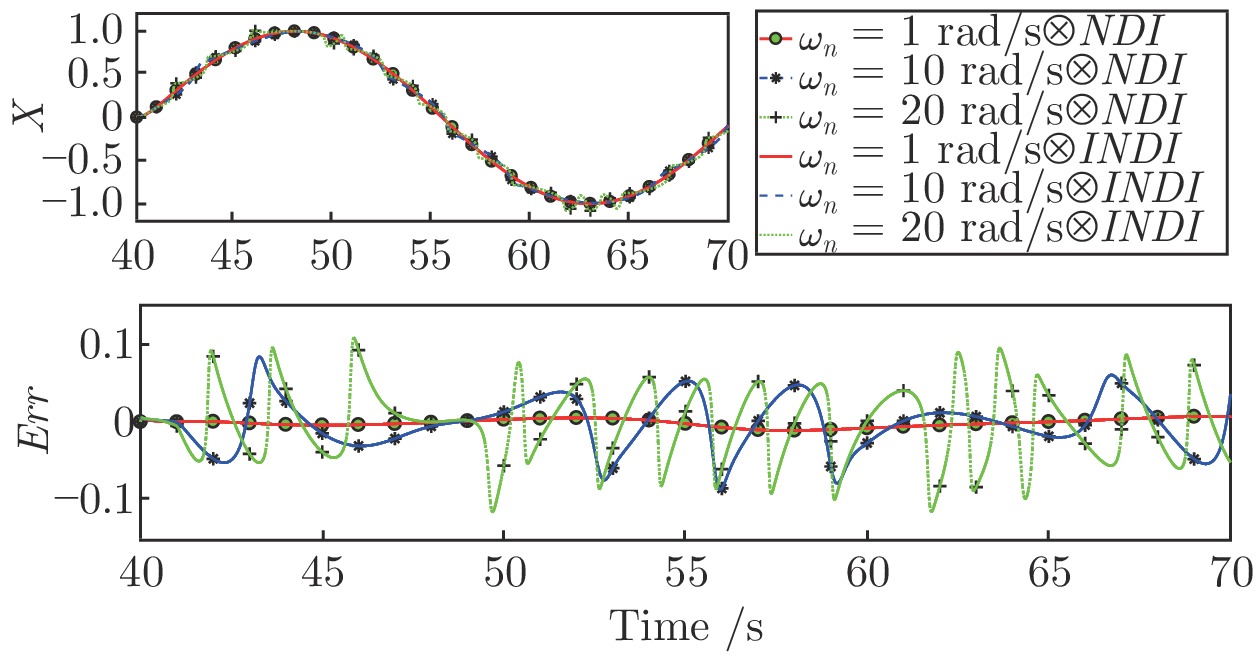
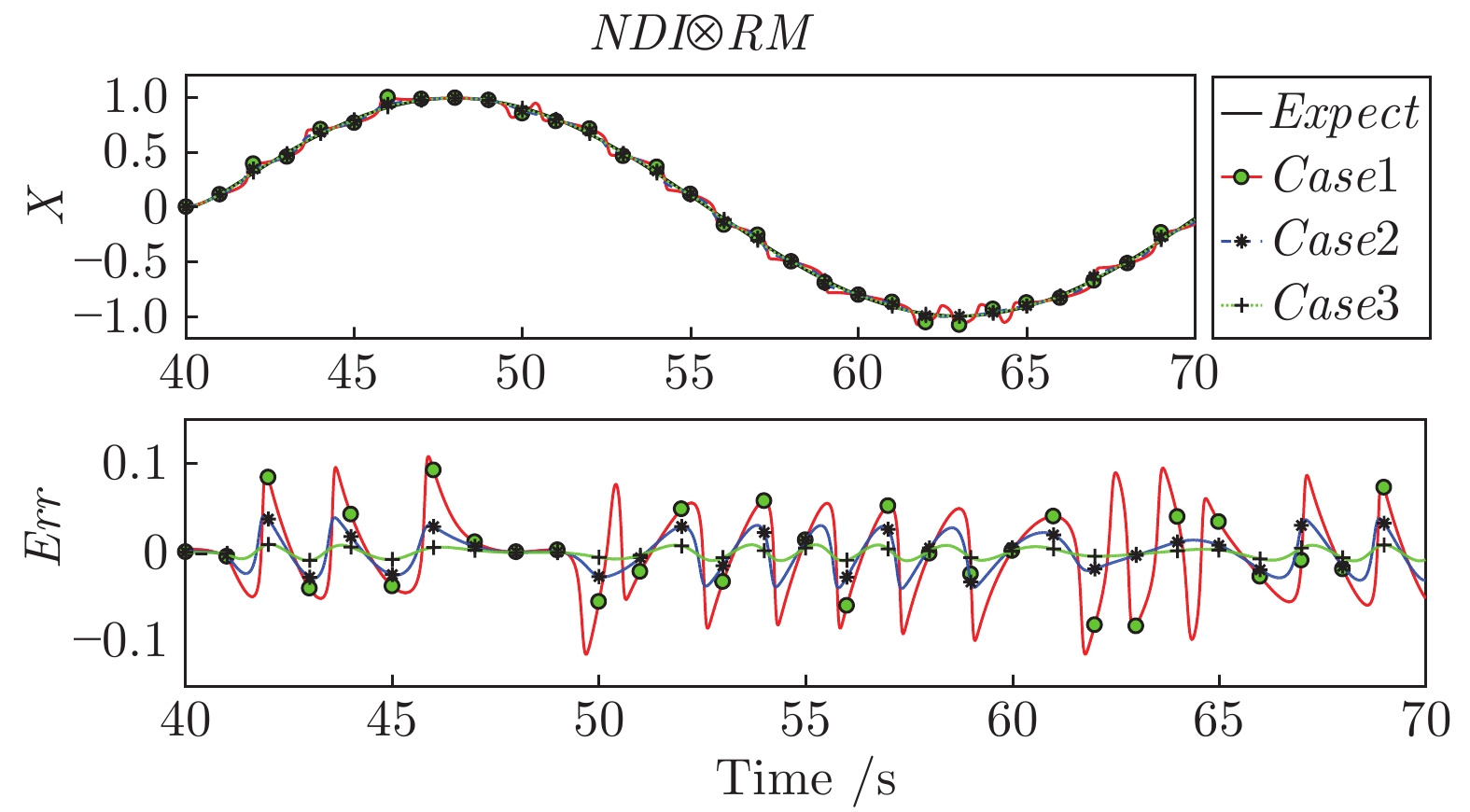
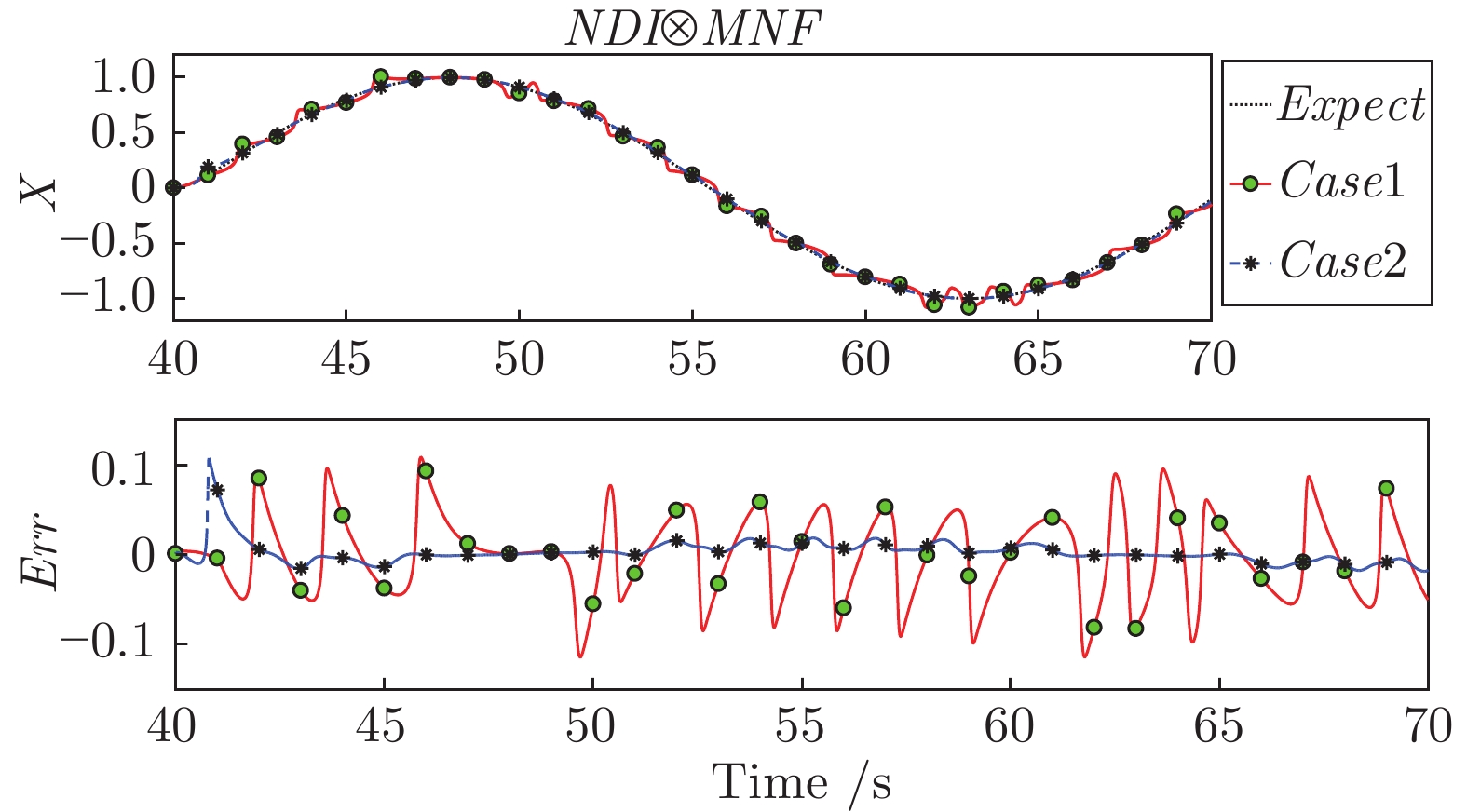
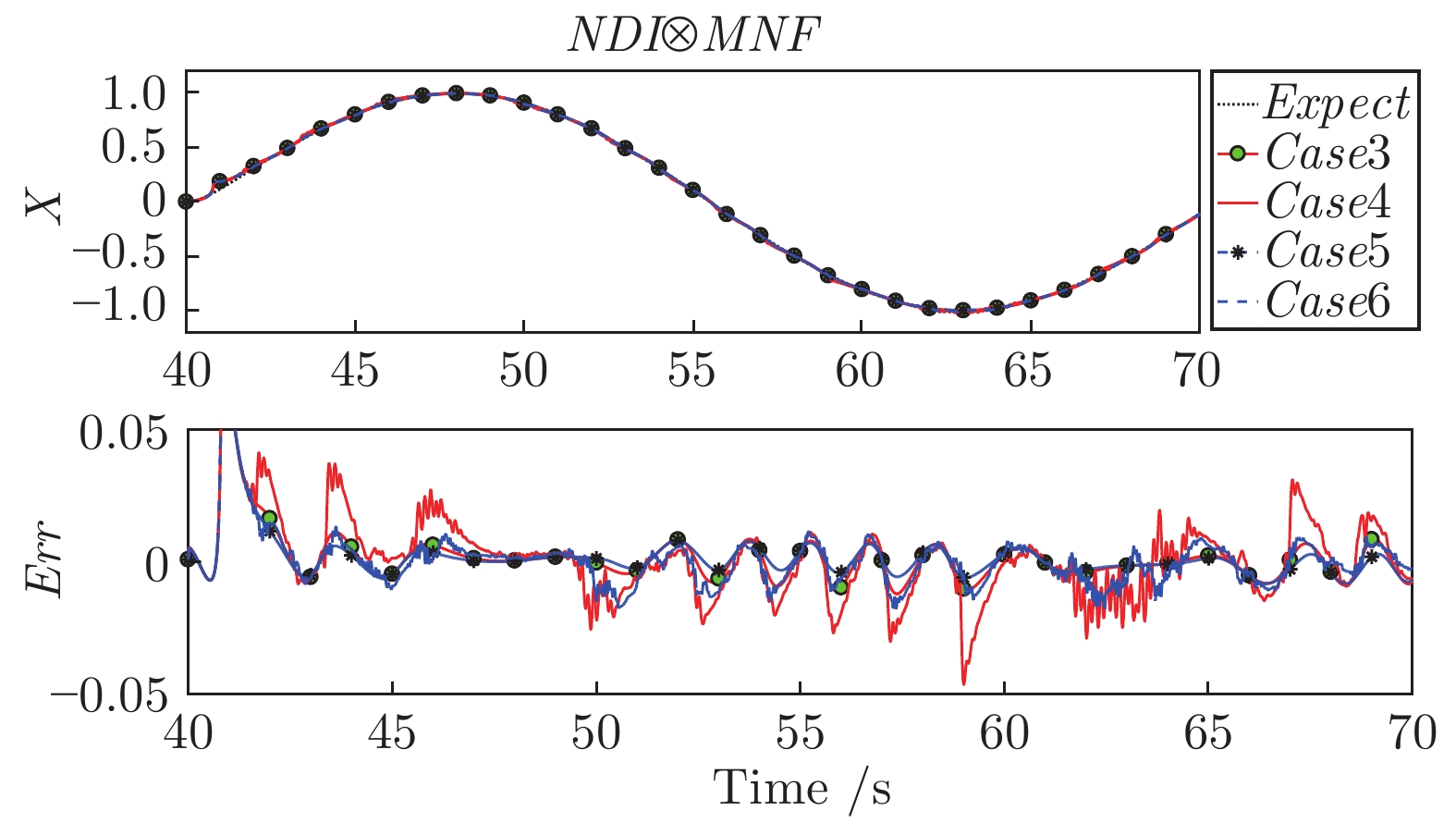
-
摘要: 本文从理论上分析了执行机构带宽对动态逆闭环控制系统动态特性影响, 发现较低的执行机构带宽会在伪线性系统中引入一个非线性干扰项, 为此提出了两种方法来消除这个非线性干扰项, 一个是采用参考模型的思想设计补偿器提高执行机构子系统的等效带宽, 另一个思路则是直接在非线性反馈项中引入补偿直接对消非线性干扰项. 仿真结果表明, 两类方法都能较好地消除非线性干扰项, 直接补偿方法能精确消除干扰项, 但需要准确动力学模型, 提高等效带宽的方法虽然是近似的, 但能方便地引入自适应算法, 可以抑制执行机构模型参数不确定的影响.Abstract: Through analyzing the influence of actuator bandwidth on dynamic characteristics of dynamic inverse close-loop control system, it is found that lower actuator bandwidth will introduce a nonlinear disturbance into pseudo-linear system, therefore, two methods are proposed to eliminate this nonlinear disturbance term, one is to use the idea of the reference model to design the compensator to improve the equivalent bandwidth of the actuator subsystem, the other idea is to introduce compensation directly into nonlinear feedback term to eliminate nonlinear disturbance. The simulation results show that both types of methods can eliminate nonlinear disturbance, the direct compensation method can accurately eliminate disturbance, but accurate dynamic model is needed, although the method by improving the equivalent bandwidth is approximate, it can easily introduce adaptive algorithm, which can restrain the influence of uncertain parameters of the actuator model.
-
在雾天采集到的图像会出现对比度降低、颜色退化、细节丢失等问题, 严重影响目标检测、自动驾驶、视频监控和遥感等户外计算机视觉系统的性能. 因此, 雾天图像复原具有重要的研究意义.
随着图像去雾方法不断发展, 可将现有方法分为基于图像增强的方法、基于图像复原的方法和基于深度学习的方法. 基于图像增强的去雾方法不考虑雾天图像退化机理, 仅仅是从空域或频域对图像进行处理, 来增强图像的对比度或对图像进行颜色校正. 常见方法有直方图均衡化[1]、Retinex算法[2]、同态滤波[3]算法等. 以上方法均未考虑图像退化原因, 直接对有雾图进行处理, 会出现颜色失真、去雾不彻底等问题.
基于图像复原的方法以大气散射模型为基础, 把图像去雾转化为估计模型参数. He等[4]提出暗通道先验理论, 能实现简单、快速去雾; Tarel等[5]借助中值滤波估计透射率, 并通过大气散射模型得到去雾图像. Zhu等[6]提出颜色衰减先验理论, 学习线性函数来预测有雾图像的深度. Berman等[7]提出一种非局部先验去雾方法. 张小刚等[8]结合双区域滤波和图像融合提出一种去雾算法, 可有效减少晕轮效应. 汪云飞等[9]借助超像素分割提高了透射率估计精度. 该类方法虽然取得了一定的效果, 但在先验假设不成立的情况下, 难以准确恢复无雾图像.
基于深度学习的方法通过在大规模数据集上训练卷积神经网络(Convolutional neural networks, CNN)来估计无雾图像. Cai等[10]和Ren等[11]构建CNN估计透射率, 并代入成像模型得到复原图像. 但其将大气光设置为全局常量, 去雾后的图像易出现伪影和颜色失真等问题. Zhang等[12]构建一种密集连接金字塔网络, 可同时估计透射率和大气光值. Li等[13]将透射率和大气光组合为一个变量K, 构建一种轻量级网络AODNet估计K. 上述方法均基于物理模型构建CNN估计变量, 这在一定程度上会限制网络的学习能力. Chen等[14]在引入平滑扩张卷积的基础上, 提出了一种端到端的门控上/下文聚合网络, 可融合不同层次的特征. Liu等[15]构建了一种基于注意力机制的多尺度网格网络, 该网络采用并行多尺度机制, 解决了串行多尺度网络中普遍存在的误差传递问题, 但该网络忽略了非相邻尺度之间的联系. Dong等[16]基于大气散射模型设计了一种特征去雾单元, 但物理模型的限制仍会在一定程度上削弱网络的学习能力. Yang等[17]通过聚合多尺度特征图来重建无雾图像, 但该网络结构较简单且需对原图进行多次下采样, 易造成图像细节丢失. 此类端到端方法可以不受物理模型的限制, 直接学习有雾−无雾图像之间的映射关系, 但仍存在感受野有限、结构信息丢失等问题, 网络聚合不同尺度特征信息的能力有待加强.
为了增大网络感受野以充分提取图像空间上/下文信息, 进而实现对目标图像更精准的预测, 多尺度端到端网络得到了广泛应用. 但现有多尺度去雾网络往往忽略了子网络感受野大小不同导致的特征信息差异, 直接将低分辨率特征与高分辨率特征进行融合. Liu等[15]采用一种注意力机制, 将各级子网络特征图由低分辨率子网络向高分辨率子网络进行逐级相加. Deng等[18]将相邻子网络生成的特征图直接相加, 再输入到基础模块进行融合. 可以发现, 该类方法直接合并各级特征图后, 小尺度网络提取到的信息在融合特征中的占比减小, 削弱了小尺度网络感受野较大的优势, 造成图像结构信息丢失, 无法准确识别较大特征目标, 出现去雾不彻底和颜色失真现象.
基于此, 本文提出一种基于误差回传机制的多尺度去雾网络. 首先, 为了提高网络识别大尺度特征目标的准确性, 设计误差回传模块(Error-backward block, EB)生成包含丰富结构信息和上/下文信息的误差图, 并用其指导大尺度子网络训练, 增大结构信息在合并特征中的占比. 现有直接融合策略和本文基于误差回传策略的多尺度网络结构如图1所示. 可以看出, 误差回传模块通过生成误差图, 实现各子网络之间的交互. 同时, 考虑到真实有雾图像雾气分布不均匀等特点, 本文设计一种雾霾感知单元(Haze aware unit, HAU), 将密集残差块与雾浓度自适应检测块(Haze density adaptive detection block, HDADB)相结合, 可识别浓雾区域和薄雾区域并据此调整去雾强度, 实现自适应去雾. 另外, 为了灵活高效复用各子网络特征, 使用门控融合模块(Gated fusion module, GFM)抑制噪声干扰, 这也是首次尝试将门控网络用于多尺度去雾特征图融合.
图 1 直接融合策略和误差回传策略示意图Fig. 1 Illustration of direct-integration strategy and error-backward strategy for multi-scale network1. 本文方法
本文提出的基于误差回传机制的多尺度去雾网络结构如图2所示. 网络包括误差回传多尺度去雾组(Error-backward multi-scale dehazing group, EMDG)、 GFM和优化模块. EMDG共有3个不同尺度的子网络, 各子网络以HAU为核心, 并设计EB实现各子网络之间的交互; 门控融合模块用于融合所有子网络的输出; 优化模块采用Unet[19]结构, 将初步去雾结果进一步优化.
图 2 基于误差回传机制的多尺度去雾网络Fig. 2 Architecture of multi-scale dehazing network based on error-backward mechanism1.1 误差回传模块
为了补充大尺度网络缺失的结构信息和上/下文信息, 本文设计了误差回传模块, 将小尺度网络提取的信息回传至大尺度网络. 如图2所示, 各尺度子网络均包含三个串联的雾霾感知单元, 除最小尺度子网络外, 所有雾霾感知单元的输出都由EB进行修正.
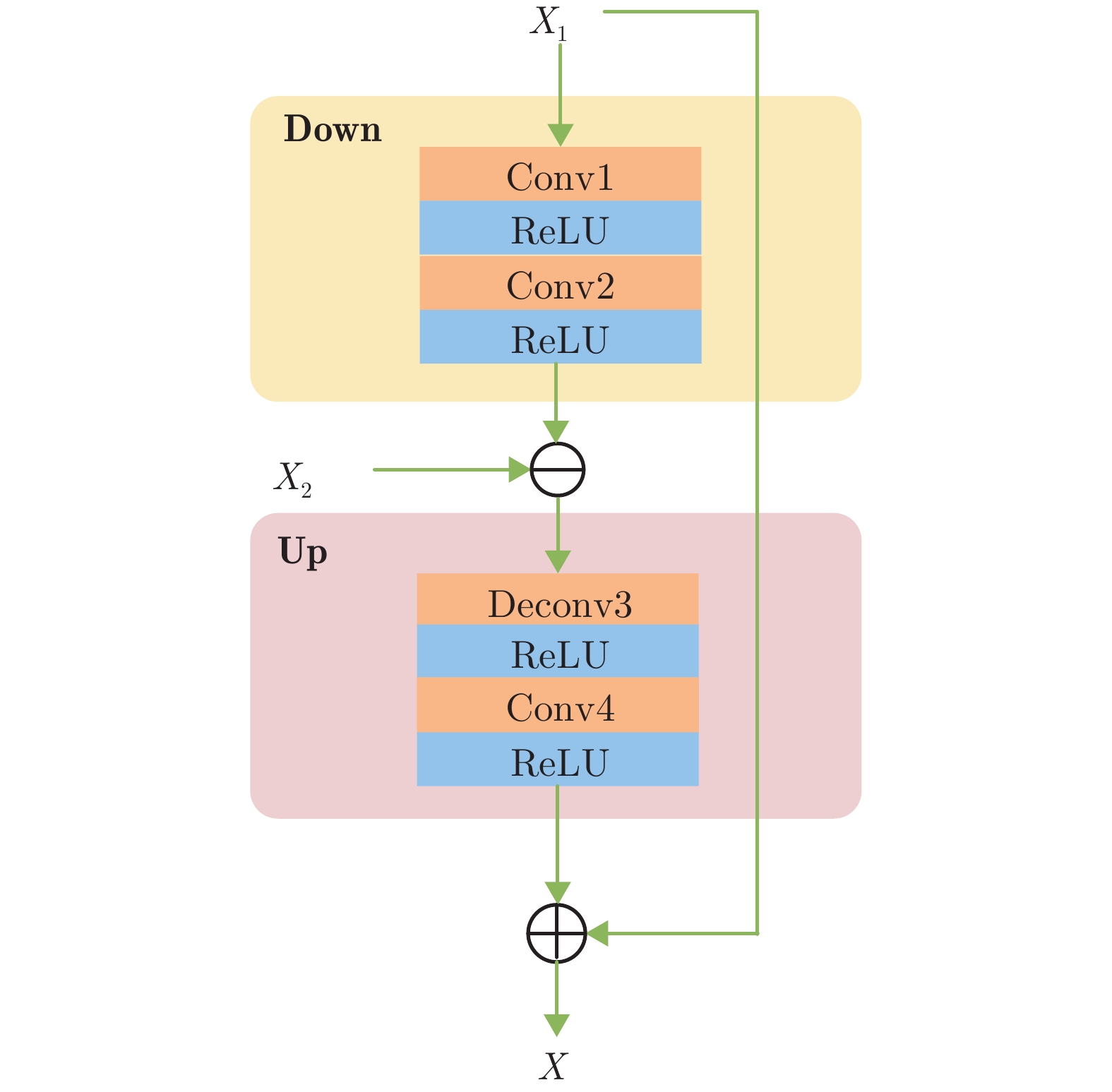
EB模块具体结构如图3所示. 首先计算高/低分辨率特征图之间的差值生成误差图, 并将误差图向上回传, 将之与高分辨率特征图进行合并, 实现对结构信息和空间上/下文信息的复用. 另外, 图2网络中每列雾霾感知单元工作的前提是其前一列单元均已完成特征提取任务, 这在增加网络深度的同时, 也可避免小尺度网络中间特征信息丢失. EB模块具体算法可表示为:
$$ X = {X_1} + {\text{Up}}[{\text{Down}}({X_1}) - {X_2}] $$ (1) 式中, $ {X_1} $代表大尺度子网络特征图, $ {X_2} $代表小尺度子网络特征图, $ {X_2} $的大小是$ {X_1} $的1/2. 如图3所示, ${\text{Down}}$表示下采样操作, 由图3中的Conv1和Conv2完成对特征图$ {X_1} $进行1/2下采样. 计算${\text{Down}}({X_1})$与$ {X_2} $的差值并将其记作误差图, 误差图中包含了大尺度子网络中缺失的特征信息. 随后, 使用${\text{Up}}$对误差图上采样, ${\text{Up}}$由Deconv3和Conv4组成, 将${\text{Up}}$输出结果反馈给大尺度子网络, 指导大尺度子网络训练. $ X $为修正后的输出, 此过程可实现对大尺度子网络所缺失的结构信息进行及时补充.
1.2 雾霾感知单元
真实场景中雾气分布通常是不均匀的, 若能区分出浓雾和薄雾区域, 便可实现高效灵活去雾. 为此, 本文设计一种雾霾感知单元, 具体结构如图4所示. HAU由残差密集块(Residual dense block, RDB)和HDADB组成. RDB采用密集连接和残差学习机制, 能够多次连接浅层和深层特征, 充分提取图像的细节特征和局部特征. HDADB通过识别某区域的雾浓度大小并据此决定对该区域的去雾强度, 可彻底地去除浓雾区域的雾气, 同时能够有效避免对薄雾区域进行过度去雾.
1.2.1 残差密集块
残差密集块由5个卷积层密集连接组成, 具体结构如图5所示. 密集连接机制可实现对浅层特征的多次复用, 同时也利于加快网络收敛. 前4个卷积层用来提取图像中包含的大量信息, 均采用3 × 3的卷积核; 最后一个卷积层用于改变特征图的通道数, 采用1 × 1的卷积核, 输出通道数为16. 所有卷积层步长均设置为1.
1.2.2 雾浓度自适应检测块
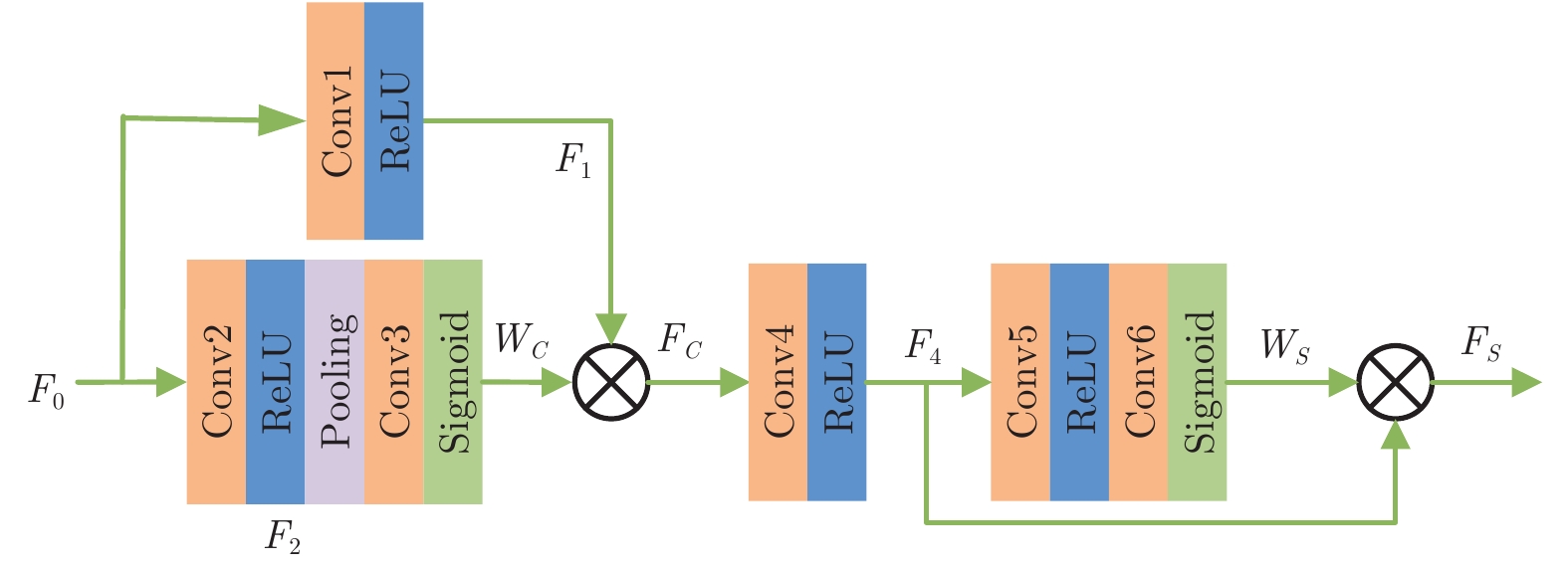
雾浓度自适应检测块包括雾浓度逐通道检测和逐像素检测, 如图6所示. 在模块前端, 逐通道检测雾浓度分布. 针对浓雾通道, 增大其特征图复用程度, 对薄雾通道则减少其复用. 具体运算过程如下:
首先, 输入特征图$ {F_0} $, 使用Conv1和Conv2分别对其进行预处理, 得到特征图$ {F_1} $和$ {F_2} $:
$$ {F_1} = {\rm{Conv}}1(\delta ({F_0})) $$ (2) $$ {F_2} = {\rm{Conv}}2(\delta ({F_0})) $$ (3) 式中, $ \delta $表示ReLU激活函数层. 随后将特征图$ {F_2} $大小由$C \times H \times W $压缩至$C \times 1 \times 1 $, 并经过非线性处理, 得到各通道权重图$ {W_C} $:
$$ {W_C} = \sigma ({\rm{Conv}}3({\text{GAP}}({F_2}))) $$ (4) 式中, $ \sigma $表示Sigmoid激活函数层, GAP (Global average pooling)表示全局平均池化.
网络训练完成后, 将各通道的权值与预处理后的$ {F_1} $逐元素相乘, 得通道加权后的特征图:
$$ {F_C} = {F_1} \times {W_C} $$ (5) 然后, 在模块后端进行逐像素雾浓度检测, 实现空域自适应去雾. 首先, 对特征图$ {F_C} $进一步提取特征, 得到:
$$ {F_4} = \delta ({\rm{Conv}}4({F_C})) $$ (6) 最后, 将尺寸为$C \times H \times W $的特征图$ {F_4} $在空间域上压缩, 其压缩后可生成尺寸为$1 \times H \times W $的权重图$ {W_S} $:
$$ {W_S} = \sigma ({\rm{Conv}}6(\delta ({\rm{Conv}}5({F_4})))) $$ (7) 网络训练的目标是使浓雾区域处的权重$ {W_S} $的值较大, 薄雾区域处权重$ {W_S} $的值较小. 使用$ {W_S} $对特征图$ {F_4} $进行加权, 可实现网络对浓雾区域重点去雾, $ {F_S} $为雾浓度自适应检测块的最终输出:
$$ {F_S} = {F_4} \times {W_S} $$ (8) 1.3 门控融合模块
不同于现有的多尺度融合方法对有效信息和干扰信息无差别对待, 本文设计的门控融合模块融合了3个不同尺度的子网络得到输出特征图, 可实现对有效信息的复用, 减少冗余信息.
如图2所示, 门控融合模块通过学习各子网络特征图的最优权重, 再对其进行加权融合, 实现对干扰信息的过滤. 将3个子网络特征图从上到下分别记为$ {J_0} $、$ {J_1} $和$ {J_2} $. 由于各尺度特征图的尺寸不同, 先利用上采样模块对$ {J_1} $和$ {J_2} $进行上采样得$ {J_1} \uparrow $和$ {J_2} \uparrow $. 上采样模块由一个步长为2的转置卷积层和一个步长为1的卷积层组成, 可将各尺度特征图恢复至相同尺寸, 并进一步提炼信息. 然后, 堆叠预处理后的特征图, 通过卷积操作逐像素判断各特征图中的干扰信息, 学习对应于$ {J_0} $、$ {J_1} \uparrow $和$ {J_2} \uparrow $的权重图$ {W_0} $、$ {W_1} $和$ {W_2} $. 特征图包含的有效信息越多, 其权重图的权值越大. 多尺度特征门控融合运算可表示为:
$$ J = {J_0} \times {W_0} + {J_1} \uparrow \times {W_1} + {J_2} \uparrow \times {W_2} $$ (9) 1.4 损失函数
本文采用了平滑L1损失和感知损失[20]. 平滑L1损失可以计算网络恢复的无雾图像与清晰图像之间的像素差值, 其在零点附近使用了平方函数, 解决了零点处导数不唯一的问题. 平滑L1损失函数可表示为:
$$ {L_S} = \frac{1}{N}\sum\limits_{x = 1}^N {\sum\limits_{i = 1}^3 {{F_S}((G{{(I))}_i}(x) - {J_i}(x))} } $$ (10) $$ {F_S}(e) = \left\{ \begin{aligned} &0.5{e^2},&{\rm{}}\;\left| e \right| < 1\; \\ &\left| e \right| - 0.5,&{\rm{否则}}\quad \end{aligned} \right. $$ (11) 式中, $ G(I) $表示网络恢复的无雾图像, $ J $表示清晰图像, $ x $表示像素点位置, $ N $表示像素个数, $i=1, 2,3$分别表示R、G、B三通道.
特征图中包含大量的语义特征和全局结构等高层信息. 本文加载ImageNet[21]预训练的VGG-16[22]网络模型, 从去雾图像和清晰图像中分别提取特征图, 将特征图间的差值作为感知损失, 借此量化去雾图像与清晰图像间的视觉误差. 感知损失函数$ {L_P} $可表示为:
$$ {L_P} = \sum\limits_{j = 1}^3 {\frac{1}{{{C_j}{H_j}{W_j}}}\left\| {{\varphi _j}(G(I)) - {\varphi _j}(J)} \right\|_2^2} $$ (12) 式中, $ J $为真实清晰图像, $ G(I) $为恢复的无雾图像, $ \varphi $为VGG-16特征提取操作, $j$为VGG网络特征图的索引标号, $ C $、$ H $和$ W $分别为图像的通道数、高度和宽度.
因此, 总损失函数为:
$$ L = {L_S} + \lambda {L_P} $$ (13) 式中, $ \lambda $为权重系数, 可以调节两个损失函数所占的比例.
2. 实验与结果分析
2.1 数据集
本文分别在RESIDE公共数据集[23]和NTIRE (New trends in image restoration and enhancement) 2018去雾挑战赛提出的O-Haze数据集[24]上训练和测试网络.
RESIDE数据集包含大量的室内有雾图像和室外有雾图像, 本文选用室内训练集(Indoor training set, ITS)和室外训练集(Outdoor training set, OTS). 其中ITS包含由1399张室内清晰图像合成的13990张室内有雾图像, OTS包含由8477张室外清晰图像合成的296695张室外有雾图像. 测试集选用SOTS (Synthetic objective testing set)测试集和HSTS (Hybird subjective testing set)合成测试集. 其中SOTS测试集包含500张室内有雾图像和500张室外有雾图像, HSTS合成测试集包含10张室外有雾图像.
O-Haze数据集共包含45张室外有雾图像及其对应的无雾图像. 根据NTIRE 2018去雾挑战赛的挑战协议, 本文选用35张有雾图像做训练集, 10张有雾图像做测试集.
为了更加客观地评价本文所提网络的去雾性能, 本文在合成数据集上计算了恢复图像与清晰图像之间的峰值信噪比(Peak signal to noise ratio, PSNR)和结构相似性(Structural similarity, SSIM).
2.2 实验设置
本文提出的去雾方法基于Pytorch框架实现, 在Win10环境下使用NVIDIA 1080Ti GPU加速网络的训练. 从每张训练图像中随机截取$220 \times 220 $像素的图像块, 作为网络的输入. 网络采用动量衰减指数$ {\beta _1}{\text{ = }}0.9 $、$ {\beta _2}{\text{ = }}0.999 $的适应性矩估计(Adaptive moment estimation, ADAM)优化器进行优化, 初始学习率设置为0.001, 在ITS上训练160个训练周期, 每20个训练周期学习率减半; 在OTS上训练10个训练周期, 每2个训练周期学习率减半; 在O-Haze上训练100个训练周期, 每10个训练周期学习率减半. 训练时的批量大小设置为8, 损失函数$ {L_P} $的权重因子$ \lambda $设置为0.04.
2.3 在合成数据集上实验
为了验证本文方法的去雾性能, 与现有的优势去雾算法进行实验对比. 将ITS中包含的全体无雾−有雾图像对用作室内训练集, 从OTS中随机选取2500张清晰图像及其对应的有雾图像作室外训练集. 随后, 采用SOTS测试集包含的500张室内有雾图像和500张室外有雾图像对模型进行测试.
在SOTS室内测试集上进行去雾评价, 并与其他方法进行对比, 结果如表1所示. 可以看出, 相比于深度学习方法, 传统暗通道先验(Dark channel prior, DCP)[4]方法去雾效果较差, PSNR和SSIM值最小; DehazeNet[10]、AODNet[13]和基于多尺度卷积神经网络(Multi-scale convolutional neural networks, MSCNN)[14]的去雾方法利用网络估计去雾模型参数, 其PSNR和SSIM较DCP有小幅提升; 增强型Pix2pix去雾网络(Enhanced Pix2pix dehazing network, EPDN)[25]、门控上/下文聚合网络(Gated context aggregation network, GCANet)[14]、GridDehazeNet[15]、基于物理模型的特征去雾网络(Physics-based feature dehazing networks, PFDN)[26]和多尺度增强去雾网络(Multi-scale boosted dehazing network, MSBDN)[26]以及本文方法均为端到端去雾网络, 评价指标有了显著提升; YNet[17]因为网络过浅, 不能充分提取图像特征, 所以表现并不突出. 在SOTS室外测试集上进行去雾评价, 结果如表2所示. 在O-Haze数据集上进行去雾评价, 结果如表3所示. 由表1、表2和表3可以看出, 相比于其他端到端网络, 本文提出的网络在几个测试集均取得了最高的PSNR值和较高的SSIM值. 其中MSBDN和GridDehazeNet因网络较深, 对SOTS测试集的拟合能力较强, 其SSIM指标略高于本文网络. 但二者对空间上/下文信息的复用程度较低, 导致其在实际去雾过程中无法准确估计大尺度特征, 在真实场景下的去雾效果并不理想.
表 1 SOTS室内测试集去雾结果的定量比较Table 1 Qualitative comparisons of dehazing results on SOTS indoor test-set方法 DCP DehazeNet AODNet EPDN GCANet PSNR (dB) 16.62 21.14 19.06 25.06 30.23 SSIM 0.8179 0.8472 0.8504 0.9232 0.9800 方法 GridDehazeNet PFDN YNet MSBDN 本文方法 PSNR (dB) 32.16 32.68 19.04 33.79 33.83 SSIM 0.9836 0.9760 0.8465 0.9840 0.9834 表 2 SOTS室外测试集去雾结果的定量比较Table 2 Qualitative comparisons of dehazing results on SOTS outdoor test-set方法 DCP DehazeNet MSCNN AODNet PSNR (dB) 19.13 22.46 22.06 20.29 SSIM 0.8148 0.8514 0.9078 0.8765 方法 EPDN GridDehazeNet YNet 本文方法 PSNR (dB) 22.57 30.86 25.02 31.10 SSIM 0.8630 0.9819 0.9012 0.9765 表 3 O-Haze数据集去雾结果定量比较Table 3 Qualitative comparisons of dehazing results on O-Haze data-set方法 DCP MSCNN AODNet EPDN GCANet GridDehazeNet 本文方法 PSNR (dB) 16.78 17.26 15.03 16.00 16.28 18.92 19.28 SSIM 0.6530 0.6501 0.5394 0.6413 0.6450 0.6721 0.6756 此外, 本文从SOTS室内测试集和室外测试集中, 分别选取4张有雾图进行主观质量评价, 各方法去雾效果如图7所示. 其中, 上面4行是室内图像去雾结果, 下面4行是室外图像去雾结果. 由于DCP方法利用暗通道先验估计透射率, 其去雾图像整体颜色偏暗, 尤其当图像中存在大面积的天空区域或白色物体时, 会出现伪影和颜色失真现象(如图7(b)中的白色桌面和天空区域). 经DehazeNet和AODNet去雾后的图像中, 仍有大量雾气残留(如图7(c)中的红色墙壁和蓝色天空), 原因是所用网络太浅, 不能充分学习图像特征. 另外, GCANet由于下采样会丢失部分高频信息(如图7(e)的桌子纹理和物体边缘), 在蓝色天空区域也会出现局部过暗的情况. 与之相似, 图7(g)中物体边缘和纹理出现模糊现象. GridDehazeNet和本文网络均可取得较好的去雾效果, 但对比图7(f)和图7(h)可以发现, 本文方法可以更好地保持图像结构信息和细节信息.
图 7 与现有方法在SOTS测试集上去雾结果对比Fig. 7 Comparisons of dehazing results with state-of-the-art methods on SOTS表4给出了本文算法与对比方法在HSTS测试集上的比较结果. 可以看出, DCP去雾效果最差, 依赖颜色投射的图像去雾(Color cast dependent image dehazing, CCDID)[27]评价指标有一定提升, 但并不显著, 本文算法取得最优PSNR和SSIM值. 图8给出了HSTS测试集中3个有雾场景下各方法的去雾结果, 其中, DCP、AODNet和EPDN产生较严重的颜色失真, DehazeNet和YNet去雾不够彻底. 相比之下, 本文算法去雾结果更接近清晰图像, 具有更好的颜色保持能力, 这是更加关注小尺度网络提取的特征信息带来的优势.
表 4 HSTS测试集去雾结果的定量比较Table 4 Qualitative comparisons of dehazing results on HSTS test-set方法 DCP DehazeNet MSCNN AODNet EPDN YNet CCDID 本文方法 PSNR (dB) 14.84 24.48 18.64 20.55 23.38 18.37 17.22 30.07 SSIM 0.7609 0.9153 0.8168 0.8973 0.9059 0.4725 0.8218 0.9658 
图 8 HSTS测试集上与现有方法去雾结果对比Fig. 8 Comparisons of dehazing results with state-of-the-art methods on HSTS2.4 在真实数据集上实验
为了验证本文提出的网络在真实场景下的适用性, 在真实有雾图像上, 对网络模型进行了测试. 由于真实数据集没有标签图像, 本文挑选了4幅真实有雾图像进行主观视觉评估, 图9给出了本文方法与目前的几种优势算法的去雾结果. 如图9(b)所示, DCP在处理包含大面积天空区域的图像时, 暗通道先验失效, 导致图像颜色失真. 如图9(d)所示, AODNet受物理模型的限制, 易导致处理后的图像饱和度过高, 恢复图像的颜色相比于原图像过于鲜艳. 同时, GCANet在恢复一些真实有雾图像的过程中, 也会产生失真现象, 例如图9(e)中第2、3幅图像的蓝色天空区域出现颜色失真以及第4幅图像远景区域过亮等. 相比于前几种方法, DehazeNet能较好地保持原图中物体的颜色, 但其对远景部分的去雾能力不足, 如图9(c)中的远山区域仍有白色雾气残留. 另外, 放大图9(f)的远景区域(如图9(f)第2幅图像的远山部分和第4幅图像远处的草地), 可以看出, GridDehazeNet处理后的图像在远景处出现一定的颜色失真. 由图9(g)可以看出, YNet因连续下采样操作, 恢复出的无雾图像部分高频信息丢失(如图9(g)第1幅图中的人脸五官不够清晰).
图 9 与现有方法在真实有雾图像上去雾结果对比Fig. 9 Comparisons of dehazing results with state-of-the-art methods on real hazy images由于采用了雾霾感知单元和误差回传机制, 本文算法可有效保持原图中丰富的结构信息和颜色信息, 尤其是对远景雾气去除效果更佳. 对比图9第4幅图像的去雾结果, 可以明显看出, 图9(b) ~ 图9(g)所示算法均不能有效去除远景雾气, 红色方框内草地上方仍有大量雾霾残留. 本文算法(见图9(h))可有效解决现有方法存在的远景区域雾气较难去除的问题, 恢复图像更为清晰自然.
2.5 消融实验和分析
为了进一步验证本文提出网络结构的合理性和各模块的必要性, 针对网络中的不同模块, 分别进行消融实验. 消融实验主要考虑的因素有: 1)每个子网络包含的RDB模块的总个数; 2)是否使用GFM模块对3个子网络的特征图进行加权融合; 3)是否使用误差回传机制, 利用低分辨率子网络改善高分辨率子网络提取特征; 4)是否使用雾浓度自适应检测块对RDB提取的特征进行逐通道雾浓度测量和逐像素雾浓度测量.
为了分析上述各因素对网络性能的影响, 以向网络中递增添加各模块的方式进行消融实验. 在ITS数据集上训练不同配置的网络(实验设置与第2.2节设置相同), 随后在SOTS室内测试集上测试模型. 测试结果的PSNR值如表5所示, 其中“√”表示包含对应该行的第1列网络模块. 表5最后一行给出了采取不同配置时, 网络在SOTS室内测试集上取得的PSNR值. 其中, 右边5列分别对应5种不同的网络配置. A列表示每个尺度子网络仅包含5个RDB模块, 各个子网络特征图直接相加; B列表示每个子网络包含5个RDB, 但采用了门控融合方法融合各子网络特征图; C列表示将每个子网络包含的RDB数量由5个变为9个; D列表示在C列配置的基础上加入了误差回传模块EB; E列较前一列加入了本文雾浓度自适应检测块HDADB, 此时网络取得的PSNR值最高, 去雾性能最佳.
表 5 基于不同模块的网络性能比较Table 5 Comparisons of network performance based on different modules模块名称 A B C D E 5个RDB √ √ — — — 9个RDB — — √ √ √ GFM — √ √ √ √ EB — — — √ √ HDADB — — — — √ PSNR (dB) 28.79 29.52 31.53 32.45 33.83 2.6 运行时间分析
为了评估本文方法的复杂性和计算效率, 在包含500张$620 \times 460$像素图像的SOTS室内测试集上进行了实验, 比较了本文算法与其他主流算法的平均运行时间, 统计结果如表6所示. 其中DCP、DehazeNet、MSCNN[14]方法在CPU上实现, 其他基于深度学习的方法在GPU上实现. 本文方法处理尺寸为$ 620 \times 460$像素图像大约需要0.73 s. 结合表6和前述实验结果可以看出, 本文方法较特征融合注意网络(Feature fusion attention network, FFANet)[28]效率显著提升, 与GridDehazeNet方法效率相当, 但去雾性能有较大提升.
表 6 各方法平均运行时间对比Table 6 Average computing time comparison of various methods方法 CPU/GPU 时间 (s) DCP CPU 25.08 DehazeNet CPU 2.56 MSCNN CPU 2.45 AODNet GPU 0.24 GridDehazeNet GPU 0.59 FFANet[28] GPU 1.23 本文方法 GPU 0.73 2.7 算法局限性分析
通过实验可以看出, 本文算法取得了较好的去雾效果. 但本文网络在处理亮度较低的图像时, 有一定概率会出现图像部分区域色度偏暗的现象, 具体情况如图10所示. 今后, 将针对这一问题, 对网络进行进一步改进.
3. 结束语
本文提出一种基于误差回传机制的多尺度去雾网络, 该网络通过构造误差回传模块, 补充高分辨率特征图缺失的结构信息和上/下文信息, 同时设计雾霾感知单元, 实现针对雾浓度的自适应去雾, 并使用门控融合模块, 以避免干扰信息对图像结构和细节的破坏, 再经优化模块, 得到最终复原图像. 在合成有雾图像和真实有雾图像上的大量实验结果表明, 本文方法恢复的图像更接近清晰图像, 解决了现有去雾方法易产生颜色失真和远景去雾不彻底的问题.
-
图 4 非线性干扰项
${{{{f}}}}\left({{x}}\right)$ 功率谱密度Fig. 4 Power spectral density of nonlinear interference term
${{{{f}}}}\left({{x}}\right)$ 
图 6 常规和增量动态逆仿真结果
Fig. 6 Conventional and incremental dynamic inverse simulation results
图 7 等效带宽方法仿真结果(
$ {\omega }_{a} $ 已知)Fig. 7 Simulation results of equivalent bandwidth method (
$ {\omega }_{a} $ Known)
图 8 等效带宽方法仿真结果(
$ {\omega }_{a} $ 未知)Fig. 8 Simulation results of equivalent bandwidth method (
$ {\omega }_{a} $ unknown)
图 9 直接补偿方法仿真结果(不考虑噪声)
Fig. 9 Simulation results of direct compensation method (Without consideration of noise)
-
[1] Meyer G, Su R, Hunt L R. Application of nonlinear transformations to automatic flight control. Automatica, 1984, 1(20): 103−107 [2] Lane S H, Stengel R F. Flight control design using nonlinear inverse dynamics. Automatica, 1988, 24(4): 471−483 doi: 10.1016/0005-1098(88)90092-1 [3] Daniel J B, Dale F E. Nonlinear control law with application to high angle-of-attack flight. Journal of Guidance, Control and Dynamics, 1992, 15(3): 761−767 doi: 10.2514/3.20902 [4] Snell S A, Nns D F, Arrard W L. Nonlinear inversion flight control for a supermaneuverable aircraft. Journal of Guidance, Control, and Dynamics, 1992, 15(4): 976−984 doi: 10.2514/3.20932 [5] Da Costa R R, Chu Q P, Mulder J A. Reentry flight controller design using nonlinear dynamic iversion. Journal of Spacecraft and Rockets, 2003, 40(1): 64−71 doi: 10.2514/2.3916 [6] Roenneke A, Well K. Nonlinear flight control for a high-lift reentry vehicle. In: Proceedings of Guidance, Navigation, and Control Conference. Munich, Germany, 1995: 1798−1805 [7] Luca A D, Lucibello P, Ulivi A G. Inversion techniques for trajectory control of flexible robotarms. Journal of Robotic Systems, 1989, 6(4): 325−344 doi: 10.1002/rob.4620060403 [8] Furuta K, Okutani T, Sone H. Computer cont-rol of a double inverted pendulum. Computer & Electrical Engineering, 1978, 5(1): 67−84 [9] Hatakeyama N, Shimada A. Movement control using zero dynamics of two-wheeled inverted pendulum robot. IEEE International Workshop on Advanced Motion Control, 2013, 44(3): 38−43 [10] Enns D, Bugajski D, Hendrick R. Dynamic inversion: an evolving methodology for flight control design. International Journal of control, 1994, 59(1): 71−91 doi: 10.1080/00207179408923070 [11] Joshua H, John V. Direct L1 adaptive nonlinear dynamic inversion control for command augmentation systems. In: Proceedings of Guidance, Navigation, and Control Conference and Exhibit. Kissimmee, Florida, USA: AIAA, 2018. [12] Geiser M, Xargay E, Hovakimyan N, Bierling T, Holzapfel F. L1 adaptive augmented dynamic inversion controller for a high agility UAV. In: Proceedings of Guidance, Navigation, and Control Conference, Portland, Oregon, USA: AIAA, 2011. [13] Yang I, Kim D, Lee D. A flight control strategy using robust dynamic inversion based on sliding mode control. In: Proceedings of Guidance, Navigation, and Control Conference and Exhibit. Mi-nneapolis, Minnesota, USA: AIAA, 2012. [14] Smith P. A simplified approach to nonlinear dynamic inversion based flight control. In: Proceedings of the 23rd Atmospheric Flight Mechanics Conference. Boston, USA: AIAA, 1998. 762−770 [15] 陈海兵, 张曙光, 方振平. 加速度反馈的隐式动态逆鲁棒非线性控制律设计. 航空学报, 2009, 30(4): 597−603 doi: 10.3321/j.issn:1000-6893.2009.04.003Chen Hai-Bing, Zhang Shu-Guang, Fang Zhen-Ping. Implitcit NDI robust nonlinear controldesign with acceleration feedback. ACTA Aeronautica et Astronautica Sinica, 2009, 30(4): 597−603 doi: 10.3321/j.issn:1000-6893.2009.04.003 [16] Grondman F, Looye G H N, Kuchar R O, Chu Q P. Design and flight testing of incremental nonlinear dynamic inversion based control laws for a passenger aircraft. In: Proceedings of Guidance, Navigation, and Control Conference and Exhibit. Kissimmee, Florida, USA: AIAA, 2018. [17] Sieberking S, Chu Q P, Mulder J A. Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction. Journal of Guidance Control and Dynamics, 2010, 33(6): 1732−1742 doi: 10.2514/1.49978 [18] 周池军, 朱纪洪. 考虑作动器动态补偿的飞机增量滤波非线性控制. 控制理论与应用, 2017, 34(5): 594−600 doi: 10.7641/CTA.2017.60402Zhou Chi-Jun, Zhu Ji-Hong. Incremental filte-red nonlinear control for aircraft with actuator dynamics compensation. Control Theory and Applications, 2017, 34(5): 594−600 doi: 10.7641/CTA.2017.60402 [19] Slotine J J, Li W, Hall P. Applied Nonlinear Control. Englewood Cliffs, NewJersey: Prentice-Hall, Inc, 1991. 120−130 [20] 韩京清. 从PID技术到自抗扰控制技术. 控制工程, 2002, 9(3): 13−18 doi: 10.3969/j.issn.1671-7848.2002.03.003Han Jing-Qing. From PID technique to active disturbances rejection control technique. Control Engineering of China, 2002, 9(3): 13−18 doi: 10.3969/j.issn.1671-7848.2002.03.003 期刊类型引用(4)
1. 任好，马亚杰，姜斌，刘成瑞. 基于零和微分博弈的航天器编队通信链路故障容错控制. 自动化学报. 2025(01): 174-185 . 
本站查看2. 罗世坚，常琪，项玥，郭胜辉. 含变化时延和集总扰动的智能网联车编队控制. 控制与决策. 2025(04): 1293-1302 . 百度学术3. 徐会彬，方龙，张莎. 车联网中基于stacking集成学习的攻击检测模型. 电信科学. 2024(12): 38-50 . 百度学术4. 张锐. 面向车联网的基于卷积神经网络的入侵检测模型. 电信科学. 2024(12): 51-62 . 百度学术其他类型引用(4)
-
下载:
下载:
计量
- 文章访问数: 935
- HTML全文浏览量: 251
- PDF下载量: 136
- 被引次数: 8
