-
摘要: 讨论现有基于模型的故障诊断与容错控制方法的局限性, 并由此提出一个基于$\nu$- 间隙度量来处理故障诊断与容错控制的新框架. 并且, 讨论了如何在此框架下对故障进行分类和分级以及提出如何进行容错控制的一般性控制结构.
-
关键词:
- 故障诊断 /
- 容错控制 /
- $\nu$- 间隙度量 /
- 鲁棒控制 /
- 系统辨识
Abstract: This paper discusses the limitations of existing model-based fault diagnosis and fault-tolerant control methods, and proposes a new framework for fault diagnosis and fault-tolerant control based on $\nu$-gap metric. The paper discusses further how to classify faults under this framework and proposes a general control structure for fault-tolerant control.-
Key words:
- Fault diagnosis /
- fault-tolerant control /
- $\nu$-gap metric /
- robust control /
- system identification
-
故障诊断与容错控制是复杂系统研究与应用的一个重要领域. 过去几十年中已经提出了很多种故障诊断与容错控制的方法, 主要包括基于数据的方法和基于模型的方法[1-3]. 本文将讨论基于模型的方法.
一般来说, 故障出现的形式被假设满足下面的标准模型:
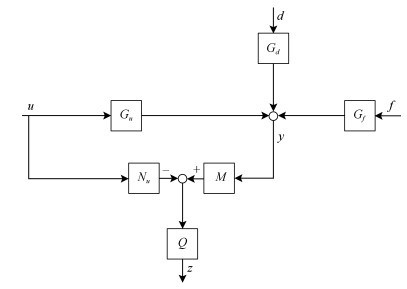
$$ \dot{{\pmb x}}=A{\pmb x}+B{\pmb u}+B_d{\pmb d}+B_f{\pmb f} $$ (1) $$ {\pmb y}=C{\pmb x}+D{\pmb u}+D_d{\pmb d}+D_f{\pmb f} $$ (2) 其中, ${\pmb x}$是系统状态, ${\pmb u}$是系统的输入, ${\pmb d}$是作用在系统上的扰动, 而${\pmb f}$是可能发生的故障信号, 故障诊断标准模型的示意图如图 1所示.
若用传递函数来表示, 即为
$$ \begin{align} {\pmb y}=G_u(s){\pmb u}+G_d(s){\pmb d}+G_f(s){\pmb f} \end{align} $$ (3) 故障诊断的目标是设计一个滤波器$F(s)$
$$ \begin{align} {\pmb z}=F(s)\begin{bmatrix}{\pmb y}\\{\pmb u}\end{bmatrix} \end{align} $$ (4) 使得残差信号${\pmb z}$满足如下条件:
1) 与输入${\pmb u}$和扰动${\pmb d}$解耦, 或者使得${\pmb u}$和${\pmb d}$对${\pmb z}$的影响越小越好;
2) 同时使得${\pmb f}$到${\pmb z}$的传输非零或者在某种意义上越大越好.
文献中通常使用的滤波器$F(s)$标准设计是一个状态观测器. 文献[2] 中给出了一个通用滤波器的设计表达式. 这个设计可以描述如下: 设式(5) 为一个稳定的左互质分解
$$ \begin{align} \nonumber&\begin{bmatrix} G_u(s)&G_d(s)&G_f(s) \end{bmatrix}=\\ & \qquad M^{-1}(s)\begin{bmatrix} N_u(s)&N_d(s)&N_f(s) \end{bmatrix} \end{align} $$ (5) 其中, $M(s)$, $N_u(s)$, $N_d(s)$和$N_f(s)$都是稳定的传递函数矩阵[4]. 则所有的故障诊断滤波器可以表示为
$$ \begin{align} F(s)=Q(s)\begin{bmatrix}M(s)&-N_u(s)\end{bmatrix} \end{align} $$ (6) 其中, $Q(s)$可以是任意稳定的正则传递函数矩阵, 如图 2所示.
那么, 故障诊断的残差信号为
$$ \begin{align} \nonumber {\pmb z}=&\ F(s)\begin{bmatrix}{\pmb y}\\{\pmb u}\end{bmatrix}=Q(s)\begin{bmatrix}M(s)&-N_u(s)\end{bmatrix}\begin{bmatrix}{\pmb y}\\{\pmb u}\end{bmatrix}= \\[1mm] &\ Q(s)N_d(s){\pmb d}+Q(s)N_f(s){\pmb f} \end{align} $$ (7) 从以上表达式可以看出, $Q(s)$的设计应该满足:
1) $Q(s)$的幅值频率响应在${\pmb d}$ (更准确地说$N_d(s){\pmb d}$) 能量显著的频段应该尽量小;
2) $Q(s)$的幅值频率响应在${\pmb f}$ (更准确地说$N_f(s){\pmb f}$) 能量显著的频段应该尽量大.
注1. 在上述故障诊断框架下, 可以得出以下结论:
1) $Q(s)$的自由度包含了所有可能的故障诊断滤波器;
2) 故障诊断滤波器$F(s)$的设计与输入信号${\pmb u}$是如何产生的无关.
由于在这个框架下, 滤波器$Q(s)$的设计与输入信号${\pmb u}$无关, 很自然提出的问题是:
1) 这个模型框架假设是否合理?
2) 系统故障是否一般可以假设为"加" 性的外部信号?
关于上述问题, 本文认为, 首先, 如果故障是个外部信号, 那么故障信号可以归结到扰动中, 容错就是抗扰问题, 故障诊断就等价于扰动估计; 其次, 无论故障是如何引起的(外部因素或者是内部因素), 故障的表现是系统内部的变化, 因此故障不可能表现为外部输入信号.
注2. 本文认为, 假设系统的故障以加法形式呈现在系统中在一般情况下并不合理. 很显然, 这是很多本领域研究者在过往研究中存在的问题[1-2, 5-6]. 因此需要将基于模型的故障诊断与容错控制研究引入正确的轨道.
本文结构如下: 第1节用几个例子说明为什么现行的故障诊断模型并非完全合理. 由此引出第2节讨论故障诊断的模型必须和系统之间的距离相关联. 第3节提出一个系统性能评价标准和系统距离的度量, 即$\nu$- 间隙度量, 以及用这些评价标准和距离度量进行故障诊断的理论基础. 第4节提出在这样的基础上进行故障分级和分类的方法. 第5节提出一个新故障诊断模型并探索可能的故障诊断的方法与容错控制一般架构. 第6节给出一些结论并提出将来探索的方向.
本文中的一些标注如下:
$$ \begin{align} \nonumber& {G}{\hspace{-1mm}\tilde{\quad}} \hspace{-1mm}(s)=G^{\rm T}(-s)\\[1mm] \nonumber&\|G(s)\|_\infty=\sup\limits_{\omega} \bar{\sigma}(G({\rm j}\omega))\end{align} $$ 1. 现行故障诊断模型的局限性
首先考虑一个闭环系统的故障诊断问题. 假设一个系统的开环故障可以用模型方程(1) 和(2) 或者方程(3) 来表示, 并假设这个系统由一个控制器$K(s)$控制. 很显然, 在这个模型下, 故障诊断滤波器(6) 可以同样应用于这个系统, 如图 3所示.
在这个模型假设下, 因为故障诊断滤波器$F(s)$的设计与${\pmb u}$是如何产生的无关, 所以故障诊断滤波器$F(s)$的设计与控制器$K(s)$也无关. 也就是说, 闭环故障诊断和开环故障诊断是一样的, 这显然是不合理的.
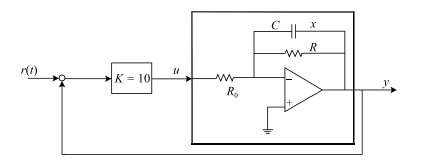
我们进一步用一个简单的例子来说明. 下面考虑一个简单的集成电路如图 4所示.
这个电路可以描述为
$$ \begin{align} \nonumber &\dot{{\pmb x}}_s=-\frac{1}{RC}{\pmb x}_s+\frac{1}{R_0C}{\pmb u}, &&\ {\pmb x}_s(0)=0\\[0mm] \nonumber &{\pmb y}=-{\pmb x}_s, ~R=\frac{R_0}{1+\delta(t)}, &&-1\leq\delta(t)\leq0 \end{align} $$ 假设$R_0C=0.2$. 并假设电路的可能故障是电阻$R$的连接. 即当$\delta(t)=0$表示电路完全正常, 而当$\delta(t)=-1$则表示电路完全断开. 传统的做法是采用模型(1), 假设故障诊断模型为
$$ \begin{align} \nonumber\dot{{\pmb x}}_m=&-\frac{1}{R_0C}{\pmb x}_m+\frac{1}{R_0C} (-\delta(t){\pmb x}_m)+\frac{1}{R_0C}{\pmb u}=\\[0mm] \nonumber &-5{\pmb x}_m+5{\pmb f}+5{\pmb u}, \quad {\pmb f} =-\delta(t){\pmb x}_m\\[0mm] \nonumber {\pmb y}_m=&-{\pmb x}_m \end{align} $$ 其中, 假设故障信号${\pmb f}=-\delta(t){\pmb x}_m$是个外加信号. 据此, 一个故障检测观测器可以设计为
$$ \begin{align} \nonumber\dot{\hat{{\pmb x}}}=&-5\hat{{\pmb x}}+5{\pmb u}+L(\hat{{\pmb y}}-{\pmb y}_m)\\[0mm] \nonumber\hat{{\pmb y}}=&-\hat{{\pmb x}} \end{align} $$ 其中, $L$是观测器增益. 则残差信号${\pmb e}_m={\pmb x}_m-\hat{{\pmb x}}$满足
$$ \begin{align} \dot{{\pmb e}}_m=-(5+L){\pmb e}_m+5{\pmb f}\nonumber \end{align} $$ 这似乎表明只要$L>0$足够大, 残差信号${\pmb e}_m$就能很快正确地检测到故障的发生(即${\pmb e}_m$跟踪${\pmb f}$). 但是事实并非如此, 因为真实测得的信号是${\pmb y}$, 不是${\pmb y}_m$. 因此真实的故障检测观测器方程为
$$ \begin{align} \nonumber\dot{\hat{{\pmb x}}}=\, &-5\hat{{\pmb x}}+5{\pmb u}+L(\hat{{\pmb y}}-{\pmb y})\\ \nonumber\hat{{\pmb y}}=\, &-\hat{{\pmb x}} \end{align} $$ 真实的残差信号${\pmb e}_r={\pmb x}_s-\hat{{\pmb x}}$满足
$$ \begin{align} \dot{{\pmb e}}_r=-(5+L){\pmb e}_r+5(-\delta(t){\pmb x}_s) \end{align} $$ (8) 为了说明真实残差信号${\pmb e}_r$与基于错误模型的残差信号${\pmb e}_m$的差异. 假设
$$ \begin{align} \nonumber \delta(t)=\begin{cases} 0, &0\leq t\leq2 \\ -1, &t>2\end{cases} \end{align} $$ 则
$$ \begin{align} \nonumber {\pmb x}_s(t)=\begin{cases} \displaystyle\int^t_0{\rm e}^{-5(t-\tau)}5{\pmb u}(\tau){\rm d}\tau, &0\leq t\leq2 \\[4mm] {\pmb x}_s(2)+\displaystyle\int^t_25{\pmb u}(\tau){\rm d}\tau, &t>2\end{cases} \end{align} $$ 由此可以看出, ${\pmb x}_s(t)$取决于输入信号${\pmb u}(t)$. 如果输入信号${\pmb u}(t)$很小或者其时间平均值很小, ${\pmb x}_s(t)$就会很小. 因此真实的残差信号${\pmb e}_r$也就会很小. 从而无法判断是否发生了故障; 另一方面, 如果输入信号${\pmb u}(t)$很大或者其时间平均值很大, 则无论是否发生故障, ${\pmb x}_s(t)$都会很大. 因此真实的残差信号${\pmb e}_r$也就会很大. 进而我们仍然无法判断是否发生了故障.
由上述例子可以得出: 把系统内部参数变化(故障) 看成是外部输入信号是不合理的.
下面我们考察上例系统在闭环情况下的故障演变过程. 假设这个简单集成电路由一个增益为$K$ $=$ $10$的闭环控制器控制, 如图 5所示.
那么这个系统的闭环系统状态方程为
$$ \begin{align} \dot{{\pmb x}}_s=-5(K+1+\delta(t)){\pmb x}_s+5Kr, \quad {\pmb x}_s(0)=0 \end{align} $$ (9) 它的时域响应如下
$$ \begin{align} {\pmb x}_s(t)= \begin{cases} \displaystyle\int^t_05K{\rm e}^{-5(K+1)(t-\tau)}{\pmb r}(\tau){\rm d}\tau, &0\leq t\leq2 \\[5mm] {\rm e}^{-5K(t-2)}{\pmb x}_s(2)+ \displaystyle\int^t_25Ke^{-5K(t-\tau)}{\pmb r} (\tau){\rm d}\tau, &t>2\end{cases}\quad \approx {\pmb r}(t) \end{align} $$ 可以看到, 这个故障对闭环系统性能的影响几乎可以忽略. 同时因为无论是否发生故障, ${\pmb x}_s(t)$都无多大变化, 从而真实的残差信号${\pmb e}_r$也无多大变化, 我们无法从残差判断是否发生了故障. 这个例子同时也印证了我们的实际经验: 故障在闭环系统中的影响与在开环系统中的影响是根本不同的.
注3. 综上, 得出以下结论:
1) 现行的故障诊断模型不够合理;
2) 基于现行的故障诊断模型进行故障检测与诊断不可行, 不能真正解决诊断问题;
3) 需要新架构和新方法;
4) 有些故障并不需要检测或诊断;
5) 需要依据故障是否需要检测建立故障的新分类方法.
2. 如何度量系统距离
综上所述, 故障是系统内部发生了变化. 它可能是系统内部一些参数的变化, 也可能是局部结构的变化. 因此从鲁棒的角度来看, 故障是系统变化, 表现出来即为系统的不确定性. 系统的容错就是使得系统具有鲁棒性. 如果系统的一个故障对系统所要实现的目标(即系统性能) 危害很小, 那么这个故障就可以认为是微小故障, 反之则可认为是小故障、中故障、大故障, 等等. 对故障危害程度的分级将对系统安全运营维护的决策提供重要的依据. 按照这样的原则, 可以对故障按其危害程度进行分级, 这种分级可以借助于不确定性与系统鲁棒性能的关系. 更进一步, 可以对故障的结构进行分类, 从而分辨出哪些故障对系统性能的影响是相近的, 哪些是有本质区别的.
很自然, 按照连续性原理, 如果一个故障对系统模型造成的差异很小(即不确定性很小), 那么它对系统性能的影响也会很小; 反之则不一定. 这一点在前述闭环集成电路的例子中可以很清楚地说明. 故障前电路系统传递函数可以描述为
$$ \begin{align} \nonumber G_0(s)=-\frac{5}{s+5} \end{align} $$ 完全故障后电路系统传递函数可以描述为
$$ \begin{align} \nonumber G_1(s)=-\frac{5}{s} \end{align} $$ 按照通常的度量, 一个系统由稳定变成不稳定是一个巨大的故障. 然而, 我们已经知道它对闭环系统性能的影响实际上是微乎其微的.
我们通过下面的例子来进一步说明传统的开环系统差异(距离) 和闭环系统差异的关系. 考虑下面三个开环系统
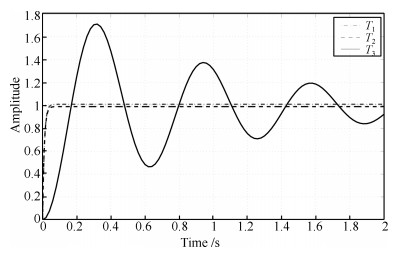
$$ \begin{align} \nonumber P_1(s)=\frac{10}{s-1}, ~~P_2(s)=\frac{10}{s+1}, ~~ P_3(s)=\frac{10}{{(s+1)}^2} \end{align} $$ 和一个控制器$K=10$, 如图 6所示. 如果从传统系统差异来看, 不稳定的$P_1$和稳定的$P_2$以及不稳定的$P_1$和稳定的$P_3$有根本区别, 而稳定的$P_2$和稳定的$P_3$似乎比较相近. 但是它们相应的闭环传递函数为
$$ \begin{align} \nonumber &T_1(s)=\frac{100}{s+99}, \quad T_2(s)=\frac{100}{s+101}\\[1mm] &T_3(s)=\frac{100}{s^2+2s+101}\nonumber \end{align} $$ 因此, 从闭环反馈控制角度来说, $P_1$和$P_2$这两个系统很近. 而$P_2$ (或者$P_1$) 和$P_3$这两个系统很远. 并且有
$$ \begin{align} \nonumber& \|T_1-T_2\|_\infty\approx0.02, \\[1mm]& \|T_1-T_3\|_\infty\approx\|T_2-T_3\|_\infty\approx5 \end{align} $$ 它们的阶跃响应分别在图 7中显示.
从以上例子可以看出, 传统系统差异的度量无法准确地预测其闭环系统性能的变化.
3. $\nu$- 间隙度量
我们需要一个新的度量从系统开环模型的差异(距离) 来判断闭环之间的差异, 因此, 首先需要确定一个度量闭环系统性能的指标.
假设$K$是一个使闭环系统镇定的控制器, 定义系统性能指标与稳定裕度为
$$ \begin{align} b_{P, K}=\left(\left\|\begin{bmatrix}I\\K\end{bmatrix}(I+PK)^{-1}\begin{bmatrix}I&P\end{bmatrix}\right\|_\infty\right)^{-1} \end{align} $$ (10) 则$b_{P, K}=b_{K, P}$, 并且$0 < b_{P, K}\leq1$.
这个指标是一个合适的闭环系统性能指标与稳定裕度. 有关这个指标的详细论述可参见文献[4].
在此, 我们列出几个比较明显的结果: $b_{P, K}>0$意味着$K$也鲁棒镇定下列不确定系统:
1) 加性不确定性. $P_a=P+\Delta_a$, 其中$P_a$与$P$具有相同的不稳定极点并且$\|\Delta_a\|_\infty < b_{P, K}$.
2) 乘性不确定性. $P_m=(I+\Delta_m)P$, 其中$P_m$与$P$具有相同的不稳定极点并且$\|\Delta_m\|_\infty < b_{P, K}$.
3) 反馈不确定性. $P_f=(I+\Delta_f)^{-1}P$, 其中$P_f$与$P$具有相同的不稳定极点并且$\|\Delta_f\|_\infty < b_{P, K}$.
4) 互质分解不确定性. $P_{fac}=(M+\Delta_m)^{-1}(N$ $+$ $\Delta_n)$, $P=M^{-1}N$并且$\|[\Delta_m~~~\Delta_n]\|_\infty < b_{P, K}$.
另外, 对于标量系统有: 增益裕度$\geq\frac{1+b_{P, K}}{1-b_{P, K}}$, 相位裕度$\geq 2{\arcsin}(b_{P, K})$.
因此, 很显然, $b_{P, K}$越大, 系统的鲁棒性能越高. 从现在起, 我们默认一个控制系统的目标就是要保持$b_{P, K}$越大越好.
给定一个被控系统$P$, 可以找到一个使$b_{P, K}$最大的最优控制器$K_{\rm opt}$. 从文献[4] 可以得到
$$ \begin{align} b_{\rm opt}(P)=\sup\limits_kb_{P, K}=\sqrt{1-\lambda_{\max}(YQ)} \end{align} $$ (11) 其中, $Y\geq0$和$Q\geq0$满足
$$ \begin{align} \nonumber &AY+YA^*-YC^*CY+BB^*=0\\[1mm] \nonumber &Q(A-YC^*C)+(A-YC^*C)^*Q+C^*C=0 \end{align} $$ 为了定义一个系统距离, 我们需要在此明确几个概念. 首先给出奈奎斯特轮廓$\Gamma$如图 8所示.
定义1. 一个标量传递函数$g(s)$的匝数$wno(g(s))$, 即为当$g(s)$在奈奎斯特轮廓$\Gamma$上取值时所画出的封闭曲线逆时针绕原点的个数(顺时针绕原点的个数记为负数).
令$\eta(g(s))$为$g(s)$在开右半平面极点个数, $\eta_0(g(s))$为$g(s)$在虚轴上的极点个数. 如果$g(s)$是双正则的, 即$g(s)$和$g^{-1}(s)$都是正则传递函数. 那么
$$ \begin{align} \nonumber wno(g)=\eta(g^{-1})-\eta(g) \end{align} $$ 即$wno(g(s))=$开右半平面零点个数- 开右半平面极点个数.
同样地, 如果$P(s)$是一个矩阵传递函数, 则$\eta(P(s))$是$P(s)$在开右半平面极点个数, $\eta_0(P(s))$是$P(s)$在虚轴上的极点个数.
定义2. 假设$P_1$和$P_2$是两个正则矩阵传递函数. 则它们的$\nu$- 间隙度量为
$$ \begin{align} & \delta_\nu(P_1, P_2)=\begin{cases} \|\Psi(P_1, P_2)\|_\infty, &\mbox{假设~1 成立}\\[1mm] 1, &\mbox{其他}\end{cases} \end{align} $$ (12) 其中
$$ \begin{align} \nonumber\Psi(P_1, P_2)=(I+P_2P_{{2}}{\hspace{-2mm}\tilde{\quad }}\hspace{-1.5mm})^{-\frac{1}{2}} (P_1-P_2)(I+{P}_{1}{\hspace{-2mm}\tilde{\quad }}\hspace{-1.5mm}P_1)^{-\frac{1}{2}} \end{align} $$ 假设1. 如果$\det(I+{P}_{{2}}{\hspace{-2mm}\tilde{\quad}}\hspace{-1.5mm}({\rm j}\omega)P_1({\rm j}\omega))\neq0, ~ \forall \omega$, 并且$wno$ $\det(I+{P}_{ {2}}{\hspace{-2mm}\tilde{\quad}}\hspace{-1.5mm}(s)P_1(s))+\eta(P_1)-\eta(P_2)-\eta_0(P_2)=0$.
如果$P_1$和$P_2$是两个标量传递函数. 则有
$$ \begin{align} \delta_v(P_1, P_2)=\sup\limits_\omega\frac{|P_1({\rm j}\omega)-P_2({\rm j}\omega)|}{\sqrt{1+|P_1({\rm j}\omega)|^2}\sqrt{1+|P_2({\rm j}\omega)|^2}}\nonumber \end{align} $$ 下面的结果是后面故障分级和分类的基础. 详细的证明参见文献[7] 以及文献[4].
引理1. 假设$(K, P)$是一个闭环镇定的系统对, $\tilde{P}$和$\tilde{K}$是扰动后的系统与控制器. 如果$\tilde{P}$和$\tilde{K}$满足$\delta_\nu(\tilde{P}, P)\leq r_P$和$\delta_\nu(\tilde{K}, K)\leq r_K$, $0\leq r_P$, $r_K$ $ < $ $1$. 则$(\tilde{P}, \tilde{K})$也是一个闭环镇定的系统对, 当且仅当
$$ \begin{align} \nonumber{\arcsin }(b_{P, K})>{\arcsin} (r_P)+{\arcsin} (r_K) \end{align} $$ 并且有
$$\begin{align} \nonumber {\rm arcsin} (b_{\tilde{P}, \tilde{K}})\geq &\ {\rm arcsin} (b_{P, K})\, -\\&\ {\rm arcsin} (r_P)-{\rm arcsin} (r_K) \end{align} $$ 以上不等式表明, 从常规度量看, 无论系统的模型有多大的变化, 只要$\nu$- 间隙度量$\delta_\nu(\tilde{P}, P)\leq r_P$足够小, 闭环系统性能变化就会很小.
在第1节和第2节的例子中:
$$ \begin{align} \nonumber&\delta_\nu(G_0, G_1)=\frac{1}{\sqrt{2}}, \quad \, \delta_\nu(10G_0, 10G_1)=0.0995\\ \nonumber& b_{\rm opt}(G_0)=0.9239, \quad b_{\rm opt}(10G_0)=0.7415 \end{align} $$ 由此可以看出, 在集成电路的故障中, 闭环系统在足够大控制器增益下, 闭环性能变化很小.
同样地, 由于
$$ \begin{align} \nonumber&\delta_\nu(P_1, P_2)=0.198\\ \nonumber&\delta_\nu(P_1, P_3)=0.7695\\ & \delta_\nu(P_2, P_3)=0.8181\notag\\[1mm] \nonumber&b_{\rm opt}(P_1)=0.6710\\ \nonumber&b_{\rm opt}(P_2)=0.7415\\ & b_{\rm opt}(P_3)=0.5464 \end{align} $$ 系统由$P_1$变化到$P_2$时, 闭环系统的性能变化不太大. 但是当系统由$P_1$ (或者$P_2$) 变化到$P_3$时, 闭环系统的性能变化有可能较大(至少无法保证变化较小).
注4. 两个系统$P_1$和$P_2$之间的$\nu$- 间隙度量可以定义为
$$ \begin{align} \nonumber \delta_\nu(P_1, P_2)=&\, \sin \sup\limits_{K\text{镇定}}|{\arcsin} (b_{P_1, K})\, -\\ &\ {\arcsin} (b_{P_2, K})| \end{align} $$ 即, 两个系统$P_1$和$P_2$之间的$\nu$- 间隙度量是对任意镇定控制所产生的性能指标的最大变化.
4. 故障分级与分类
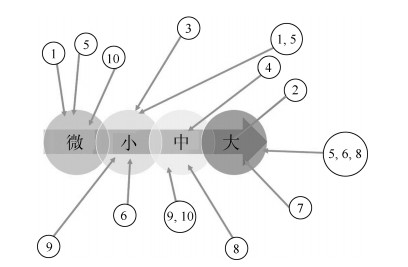
利用上面定义的$\nu$- 间隙度量可以对一个系统可能发生的故障集合进行分级与分类. 假设系统的标称模型为$P$, 故障发生后可能的模型为
$$ \begin{align} \nonumber\tilde{P}\in\{P_1, P_2, \cdots, P_{10}, P_{1, 5}, P_{9, 10}, P_{5, 6, 8}\} \end{align} $$ 其中, $\{P_1, P_2, \cdots, P_{10}\}$表示故障$1, 2, \cdots, 10$单独发生时的模型, $P_{1, 5}$表示故障1和故障5同时或者相继发生后的系统模型, 以此类推.
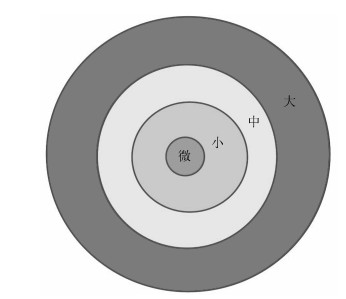
如果故障后的模型与标称模型之间的$\nu$- 间隙度量很小, 我们就认为是微小故障. 否则认为是小故障、中故障、大故障, 等等. 故障集合可以按照各个故障对系统性能影响的危害程度分成若干个等级, 如图 9所示.
图 10显示了按照故障系统相对原系统的$\nu$- 间隙度量距离分成故障各等级:
$$ \begin{align} &1)~ \mbox{微小故障}: &&\delta_\nu(P, \tilde{P})\leq\xi_1\\ & 2)~\mbox{小故障:}&& \xi_1\leq\delta_\nu(P, \tilde{P})\leq\xi_2\\ &3)~\mbox{中等故障:}&& \xi_2\leq\delta_\nu(P, \tilde{P})\leq\xi_3\\ &4)~\mbox{大故障:} &&\xi_3\leq\delta_\nu(P, \tilde{P})\leq\xi_4\\ &\qquad\quad\vdots \end{align} $$ 一个故障集合究竟要分成多少个等级以及如何确定每个等级的阈值$\xi_i$, 取决于具体的问题.
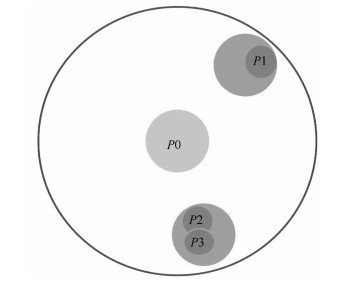
同一个级别的故障, 其闭环特性也会有所不同. 因此我们将对同级别故障进行分类. 微小故障显然具有相同的闭环特性, 因此属于同类. 而小故障、中故障、大故障即使是同级, 也可能具有本质上不同的闭环特性, 因此属于不同类别. 图 11中显示了4个不同的故障: 微小故障$P_0$, 严重故障$P_1$, $P_2$, $P_3$. 虽然$P_1$, $P_2$, $P_3$都是严重故障, 但$P_2$和$P_3$之间的$\nu$- 间隙距离, 即$\delta_\nu$ $(P_2, P_3)$很小. 因此故障$P_2$下的闭环系统与故障$P_3$下的闭环系统具有相近的闭环特性. 另一方面, $P_1$和$P_2$之间的$\nu$- 间隙距离以及$P_1$和$P_3$之间的$\nu$- 间隙距离都很大, 因此故障$P_2$下(或者故障$P_3$下) 的闭环系统特性和故障$P_1$下的闭环系统特性可能会有非常大的差异. 因此$P_2$与$P_3$属于同类同级故障, 而$P_1$与$P_2$ (或者$P_3$) 是同级但不同类故障. 故障分级和分类对容错控制策略的设计至关重要. 很显然, 同类的故障只需要一个容错控制器.
5. 一个故障诊断模型
上述分析表明, 故障诊断领域过去一直沿用的模型(1)~(3) 并不真正实用. 用这样的模型无法给实际系统中出现的故障建模. 我们认为一个系统中的任何故障都是由于系统内部发生了变化, 而不是外部输入信号所能为的. 这种变化一般都可以用系统的参数变化来表达. 本模型中, 我们假设: 故障总是可以用参数$\delta_i\in[-1, 0]$, $i=1, \cdots, m$表征, 其中, 1) $\delta_i=0$表示无故障; 2) $\delta_i=-1$表示全故障; 3) $-1$ $ < $ $\delta_i < 0$表示中间故障(或者部分故障).
一般故障诊断模型可以用图 12表示. 它的输入输出形式为
$$ \begin{align} &\begin{bmatrix}{\pmb z}\\{\pmb y}\end{bmatrix}=G(s)\begin{bmatrix}{\pmb\omega}\\{\pmb d}\\{\pmb u}\end{bmatrix}\nonumber\end{align} $$ $$ \begin{align} \nonumber &{\pmb \omega}={\Delta} {\pmb z} \end{align} $$ 或
$$ \begin{align} {\pmb y}=G_d(s, {\Delta}){\pmb d}+G_u(s, {\Delta}){\pmb u} \end{align} $$ (13) 其中, ${\Delta}={\rm diag}\{\delta_1I_{r_1}, \delta_2I_{r_2}, \cdots, \delta_mI_{r_m}\}$, ${\pmb d}$表示所有外部扰动, ${\pmb u}$表示所有系统输入, ${\pmb y}$表示所有可测输出信号(包括常规输出和任何对故障诊断有用的信号).
在这个模型的假设下, 故障诊断可以认为是参数估计问题. 设
$$ \begin{align} \nonumber{\pmb \delta}(t)=[\delta_1(t), \delta_2(t), \cdots, \delta_m(t)]^{\rm T} \end{align} $$ 特别是在单输入单输出时, 如果参数方程可以关联为线性方程
$$ \begin{align} \nonumber { \phi}(t)={\pmb\delta}^{\rm T}(t){\pmb\psi}(t)+{ n}(t) \end{align} $$ 其中, ${ \phi}(t)$和${\pmb\psi}(t)$可以从输入输出数据计算出, ${ n}(t)$是噪声或扰动. 一个估计${\pmb \delta}(t)$的离散方法可以用最小二乘算法, 即
$$ \begin{align} {\pmb \delta}(t)={\rm arg min} \sum^t_{j=t-N}({ \phi}(j)-{\pmb \delta}^{\rm T}(t){\pmb\psi}(j))^2 \end{align} $$ (14) 其中, $N$是实时计算的时间窗口. 但具体算法尚待进一步探讨.
在获得故障诊断、故障分级和故障分类等信息的基础上, 我们可以利用文献[8-10] 中提出的高性能控制结构给出图 13中容错控制的一般构架.
其他控制器设计参见文献[8-10]. 这些具体设计也是有待进一步研究的课题.
6. 结论
本文通过简单的系统论述了过去沿用的故障诊断模型并不真正实用的原因, 其并不能正确地为故障系统建立诊断模型. 并由此提出了一个新的故障诊断建模方法, 以及故障分级和分类的算法. 最后, 在此基础上提出了一个容错控制的一般控制架构.
另外, 如果把本文中的$\nu$- 间隙度量($\nu$-gap) 换成间隙度量(gap)[11-15], 则所有的论述仍然成立. 但间隙度量(gap) 相对更保守, 计算起来更复杂. 更重要的是, $\nu$- 间隙度量与频率响应有着密切联系, 具有推出更不保守结果的潜能, 因此, 使用$\nu$- 间隙度量会有更进一步的探索空间.
-
-
[1] Chen J, Patton R. Robust Model-Based Fault Diagnosis for Dynamic Systems. Springer, 1999. [2] Ding S X. Model-Based Fault Diagnosis Techniques -Design Schemes, Algorithms and Tools. 2nd Edition, Springer-Verlag, London, 2013. [3] Ding S X. Data-Driven Design of Fault Diagnosis and Fault-Tolerant Control Systems. Springer-Verlag, London, 2014. [4] Zhou K. Essentials of Robust Contro. Prentice-Hall, Englewood Cliffs, NJ, 1998. [5] Liu N, Zhou K. Optimal robust fault detection for linear discrete time systems. Journal of Control Science and Engineering, 2008, 2008(7): 1-16 http://ieeexplore.ieee.org/document/4434125/citations [6] Li X, Zhou K. A time domain approach to robust fault detection of linear time-varying systems. Automatica, 2009, 45(1): 94-102 doi: 10.1016/j.automatica.2008.07.017 [7] Vinnicombe G. Uncertainty and Feedback: Hinf Loop-Shaping and the V-Gap Metric. World Scientific, 2000. [8] Zhou K, Ren Z. A new controller architecture for high performance, robust, adaptive, and fault tolerant control. IEEE Transactions on Automatic Control, 2001, 46(10): 1613-1618 doi: 10.1109/9.956059 [9] Zhou K. A new approach to robust and fault tolerant control. Acta Automatica Sinca, 2005, 31(1): 43-55 [10] 周克敏. 鲁棒控制: 回顾与展望(黄琳院士主编《中国学科发展战略: 控制科学》第十二章). 科学出版社, 2015.Zhou K M. Robust control: Retrospect and prospect, (Huang Lin as Editor-in-Chief of the Chinese Discipline Development Strategy: Control Science, Chapter 12), Science Press, 2015. [11] Ding S X, Yang, Y, Zhang Y, Li L. Data-driven realization of kernel and image representations and their application to fault detection and control system design. Automatica, 2014, 50: 2615-2623 doi: 10.1016/j.automatica.2014.08.022 [12] Ding S X. Application of factorization and gap metric techniques to fault detection and isolation, Part Ⅰ and Part 2. IFAC Conference Paper Archive, 2015, 48(21): 113-124 http://www.sciencedirect.com/science/article/pii/S2405896315016420 [13] Georgiou T T. On the computation of the gap metric. Systems and Control Letters, 1988, 11: 253-257 doi: 10.1016/0167-6911(88)90067-9 [14] Georgiou T T, Smith M C. Optimal robustness in the gap metric. IEEE Transactions on Automatic Control, 1990, 35: 673-686 doi: 10.1109/9.53546 [15] Koenings T, Krueger M, Luo H, Ding S X. A data-driven computation method for the gap metric and the optimal stability margin. IEEE Transactions on Automatic Control, 2018, 63(3): 805-810 doi: 10.1109/TAC.2017.2735023 期刊类型引用(8)
1. 张莹,郭楚佳,马力文. 基于间隙度的变换器早期故障诊断方法. 科学技术与工程. 2023(04): 1542-1548 .  百度学术
百度学术2. 钟麦英,王钦,彭涛,席霄鹏,杨超,薛婷. 高速列车牵引传动系统运行状态监测技术综述. 山东科技大学学报(自然科学版). 2023(02): 88-97 .  百度学术
百度学术3. 郑帅,杨雪纯,海丹凤. 基于改进密度峰值聚类算法的低占用率云调度容错控制模型研究. 桂林航天工业学院学报. 2023(03): 400-405 .  百度学术
百度学术4. 郭云鹤,魏文程,覃珍妮,李浩然,李桐. 存在丢包的非线性网络控制系统闭环故障检测. 火力与指挥控制. 2023(08): 32-39+47 .  百度学术
百度学术5. 高明,周东华,张森,盛立. 三容水箱液位控制系统的间歇故障检测实验教学设计. 实验技术与管理. 2022(09): 186-190 .  百度学术
百度学术6. 王海风,郑柏超,卢世堃,赖琛. 基于观测器的无人机编队自适应容错控制. 电子测量技术. 2022(17): 56-64 .  百度学术
百度学术7. 余伟,江艳,张凡. 间隙度量模式下的闭环系统故障诊断实现. 控制理论与应用. 2022(12): 2293-2301 .  百度学术
百度学术8. 李雅,侯彦东,刘畅. 基于故障程度的自适应优化容错控制. 计算机工程与应用. 2021(23): 295-302 .  百度学术
百度学术其他类型引用(16)
-






 下载:
下载:






 下载:
下载:
