基于RISE反馈的串联弹性驱动器最优控制方法

孙雷; 孙伟超; 王萌; 刘景泰

doi:10.16383/j.aas.2018.c170146

基于RISE反馈的串联弹性驱动器最优控制方法

doi: 10.16383/j.aas.2018.c170146

孙雷^1,2, ,,
孙伟超^1,2,,
王萌^1,2,,
刘景泰^1,2,

1.
南开大学机器人与信息自动化研究所天津 300350
2.
天津市智能机器人技术重点实验室天津 300350

基金项目:

国家自然科学基金 61573198

详细信息

作者简介:
孙伟超  南开大学机器人与信息自动化研究所硕士生.主要研究方向为机器人控制系统.E-mail:sun@mail.nankai.edu.cn

王萌  南开大学机器人与信息自动化研究所博士研究生.主要研究方向为SEA力矩控制, 人机交互, 单足跳跃机器人.E-mail:wmkevin@mail.nankai.edu.cn

刘景泰  博士, 南开大学机器人与信息自动化研究所教授.主要研究方向为机器人学, 机器人控制.E-mail:liujt@nankai.edu.cn

通讯作者:
孙雷博士, 南开大学机器人与信息自动化研究所副教授.主要研究方向为机器人控制系统.本文通信作者.E-mail:sunl@nankai.edu.cn

计量
- 文章访问数: 2744
- HTML全文浏览量: 270
- PDF下载量: 618
- 被引次数: 73
出版历程
- 收稿日期: 2017-03-17
- 录用日期: 2017-09-15
- 刊出日期: 2018-12-20

Optimal Control for Series Elastic Actuator Using RISE Feedback

SUN Lei^{1,2
, ,},
SUN Wei-Chao^{1,2
,},
WANG Meng^{1,2
,},
LIU Jing-Tai^{1,2
,}

1.
Institute of Robotics and Automatic Information System, Nankai University, Tianjin 300350
2.
Tianjin Key Laboratory of Intelligent Robotics, Tianjin 300350

Funds:

National Natural Science Foundation of China 61573198

More Information

Author Bio:
Master student at the Institute of Robotics and Automatic Systems, Nankai University. His research interest covers robot control systems

Ph. D. candidate at the Institute of Robotics and Automatic systems, Nankai University. His research interest covers SEA torque control, human-robot interaction, and monopod hopping robot

Ph. D., professor at the Institute of Robotics and Automatic Systems, Nankai University. His research interest covers robotics and robot control

Corresponding author: SUN Lei Ph. D., associate professor at the Institute of Robotics and Automatic Systems, Nankai University. His research interest covers robot control systems. Corresponding author of this paper

摘要

摘要: 串联弹性驱动器（Series elastic actuator，SEA）是机器人交互系统中的一种理想力源.本文针对非线性SEA的力矩控制问题提出一种基于RISE（Robust integral of the sign of the error）反馈的最优控制方法，能够克服模型参数不确定和有界扰动，实现SEA输出力矩在交互过程中快速平稳地收敛到期望值.具体来说，首先对SEA的模型进行分析和变换；然后假设模型参数和扰动均已知，并在此基础上基于二次型指标设计最优控制律；之后基于RISE反馈重新设计控制律抵消模型参数不确定性和有界扰动，基于Lyapunov理论分析控制器的收敛性和信号的有界性，实验结果表明这种基于RISE反馈的最优控制方法具有良好的控制性能和对有界扰动的鲁棒性.
- 串联弹性驱动器 /
- 最优控制 /
- RISE /
- 力矩控制
Abstract: Series elastic actuator (SEA) is an ideal power source in robots interaction systems. Aiming at SEA torque control, an optimization scheme with an RISE (robust integral of the sign of the error) feedback structure is proposed to ensure the output of SEA asymptotically tracks a desired time-varying torque despite uncertainties in the dynamics like bounded disturbance or parametric uncertainty. Specifically, the generic dynamics of SEA system is described and some analysis and transformation operations are performed. The system in which all terms are assumed to be known is feedback linearized and a control law is developed using the optimization method for a given quadratic performance index. Then the control law is modified to contain the RISE feedback term for identifying the uncertainty. At last, a Lyapunov stability analysis is included to show that the tracking error converges to zero with all signals bounded. Experiment results show that the suggested controller achieves satisfactory control performance and strong robustness to disturbance.
- Series elastic actuator (SEA) /
- optimal control /
- robust integral of the sign of the error (RISE) /
- torque control
注释:

1) 本文责任编委郭戈

HTML全文

本文责任编委郭戈

图 1 SEA示意图

Fig. 1 Structure of SEA

下载: 全尺寸图片幻灯片

图 2 阶跃信号仿真结果

Fig. 2 Simulink result of step signal

下载: 全尺寸图片幻灯片

图 3 RISE反馈项与实际未知项对比结果

Fig. 3 Comparison result of RISE feedback term with disturbance term

下载: 全尺寸图片幻灯片

图 4 SEA实验平台

Fig. 4 SEA testbed

下载: 全尺寸图片幻灯片

图 5 SEA弹性结构

Fig. 5 Elastic structure of SEA

下载: 全尺寸图片幻灯片

图 6 环境交互实验结果

Fig. 6 Experiment result of robot-environment-interaction

下载: 全尺寸图片幻灯片

图 7 电机与负载运动情况

Fig. 7 Motion result of motor and load

下载: 全尺寸图片幻灯片

图 8 人机交互实验结果

Fig. 8 Experiment result of human-robot-interaction

下载: 全尺寸图片幻灯片

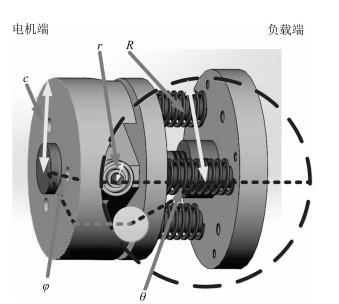
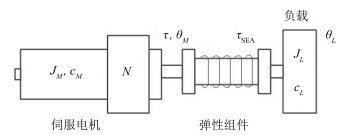
表 1 SEA机械参数

Table 1 Mechanical parameter of SEA

Parameter	Value	Uanit
$J_M$	$0.082$	kgm$^2$
$c_M$	$0.75$	kgm$^2$/s
$Ks$	$13\, 600$	N/m
$c$	$0.018$	m
$R$	$0.020$	m
$r$	$0.005$	m

下载: 导出CSV

参考文献(32)

[1]	Veneman J F, Ekkelenkamp R, Kruidhof R, Van Der Helm F C, Van Der Kooij H. A series elastic-and Bowden-cable-based actuation system for use as torque actuator in exoskeleton-type robots. International Journal of Robotics Research, 2006, 25(3):261-281 doi: 10.1177/0278364906063829
[2]	Vallery H, Veneman J F, Van Asseldonk E, Buss R M, Van Der Kooij H. Compliant actuation of rehabilitation robots. IEEE Robotics and Automation Magazine, 2008, 15(3):60-69 doi: 10.1109/MRA.2008.927689
[3]	Sulzer J S, Roiz R A, Peshkin M A, Patton J L. A highly backdrivable, lightweight knee actuator for investigating gait in stroke. IEEE Transactions on Robotics, 2009, 25(3):539-548 doi: 10.1109/TRO.2009.2019788
[4]	Mathijssen G, Lefeber D, Vanderborght B. Variable recruitment of parallel elastic elements:series-parallel elastic actuators (SPEA) with dephased mutilated gears. IEEE/ASME Transactions on Mechatronics, 2015, 20(2):594-602 doi: 10.1109/TMECH.2014.2307122
[5]	Pfeifer S, Pagel A, Riener R, Vallery H. Actuator with angle-dependent elasticity for biomimetic transfemoral prostheses. IEEE/ASME Transactions on Mechatronics, 2015, 20(3):1384-1394 doi: 10.1109/TMECH.2014.2337514
[6]	Pratt G A, Williamson M M. Series elastic actuators. In: Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems 95. Pittsburgh, PA, USA: IEEE, 1995. 399-406 http://www.mendeley.com/catalog/series-elastic-actuators/
[7]	Pratt G A, Willisson P, Bolton C, Hofman A. Late motor processing in low-impedance robots: impedance control of series-elastic actuators. In: Proceedings of the 2004 American Control Conference. Boston, MA, USA: IEEE, 2004. 3245-3251 http://www.mendeley.com/catalog/late-motor-processing-lowimpedance-robots-impedance-control-serieselastic-actuators/
[8]	Wyeth G. Control issues for velocity sourced series elastic actuators. In: Proceedings of the 2006 Australasian Conference on Robotics and Automation. Auckland, New Zealand: Australian Robotics and Automation Association Inc., 2006. 1-6
[9]	Wyeth G. Demonstrating the safety and performance of a velocity sourced series elastic actuator. In: Proceedings of the 2008 IEEE International Conference on Robotics and Automation (ICRA). Pasadena, CA, USA: IEEE, 2008. 3642-3647 http://www.mendeley.com/catalog/demonstrating-safety-performance-velocity-sourced-series-elastic-actuator/
[10]	Vallery H, Ekkelenkamp R, Van der Kooij H, Buss M. Passive and accurate torque control of series elastic actuators. In: Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). San Diego, CA, USA: IEEE, 2007. 3534-3538 http://www.mendeley.com/catalog/passive-accurate-torque-control-series-elastic-actuators/
[11]	Tagliamonte N L, Accoto D. Passivity constraints for the impedance control of series elastic actuator. Proceedings of Institution of Mechanical Engineers, Part Ⅰ:Journal of Systems and Control Engineering, 2013, 228(3):138-153
[12]	Kong K, Bae J, Tomizuka M. Control of rotary series elastic actuator for ideal force-mode actuation in human-robot interaction applications. IEEE/ASME Transactions on Mechatronics, 2009, 14(1):105-118 doi: 10.1109/TMECH.2008.2004561
[13]	Kong K, Bae J, Tomizuka M. A compact rotary series elastic actuator for human assistive systems. IEEE/ASME Transactions on Mechatronics, 2012, 17(2):288-297 doi: 10.1109/TMECH.2010.2100046
[14]	Yoo S, Chung W K. SEA force/torque servo control with model-based robust motion control and link-side motion feedback. In: Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA). Seattle, WA, USA: IEEE, 2015. 1042-1048 http://www.mendeley.com/catalog/sea-forcetorque-servo-control-modelbased-robust-motion-control-linkside-motion-feedback/
[15]	Calanca A, Fiorini P. Human-adaptive control of series elastic actuators. Robotica, 2014, 32(8):1301-1316 doi: 10.1017/S0263574714001519
[16]	Bae J, Kong K, Tomizuka M. Gait phase-based smoothed sliding mode control for a rotary series elastic actuator installed on the knee joint. In: Proceedings of the 2010 American Control Conference (ACC). Baltimore, MD, USA: IEEE, 2010. 6030-6035 http://www.mendeley.com/catalog/gait-phasebased-smoothed-sliding-mode-control-rotary-series-elastic-actuator-installed-knee-joint/
[17]	Misgeld B J E, Pomprapa A, Leonhardt S. Robust control of compliant actuators using positive real H2-controller synthesis. In: Proceedings of the 2014 American Control Conference (ACC). Portland, OR, USA: IEEE, 2014. 5477-5483 https://ieeexplore.ieee.org/document/6858609
[18]	朱秋国, 熊蓉, 吕铖杰, 毛翊超.新型串联弹性驱动器设计与速度控制.电机与控制学报, 2015, 19(6):83-88 http://d.old.wanfangdata.com.cn/Periodical/djykzxb201506013 Zhu Qiu-Guo, Xiong Rong, Lv Cheng-Jie, Mao Yi-Chao. Novel series elastic actuator design and velocity control. Electric Machines and Control, 2015, 19(6):83-88 http://d.old.wanfangdata.com.cn/Periodical/djykzxb201506013
[19]	Wolf S, Hirzinger G. A new variable stiffness design: matching requirements of the next robot generation. In: Proceedings of the 2008 IEEE International Conference on Robotics and Automation (ICRA). Pasadena, CA, USA: IEEE, 2008. 1741-1746 http://www.mendeley.com/catalog/new-variable-stiffness-design-matching-requirements-next-robot-generation/
[20]	Jafari A, Tsagarakis N G, Caldwell D G. A novel intrinsically energy efficient actuator with adjustable stiffness (AwAS). IEEE/ASME Transactions on Mechatronics, 2013, 18(1):355-365 doi: 10.1109/TMECH.2011.2177098
[21]	Mooney L, Herr H. Continuously-variable series-elastic actuator. In: Proceedings of the 2013 IEEE International Conference on Rehabilitation Robotics (ICORR). Seattle, WA, USA: IEEE, 2013. 1-6 https://www.ncbi.nlm.nih.gov/pubmed/24187221
[22]	Paine N, Sentis L. A new prismatic series elastic actuator with compact size and high performance. In: Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO). Guangzhou, China: IEEE, 2012. 1759-1766 http://www.mendeley.com/catalog/new-prismatic-series-elastic-actuator-compact-size-high-performance/
[23]	Laffranchi M, Chen L S, Kashiri N, Lee J, Tsagarakis N G, Caldwell D G. Development and control of a series elastic actuator equipped with a semi active friction damper for human friendly robots. Robotics and Autonomous Systems, 2014, 62(12):1827-1836 doi: 10.1016/j.robot.2014.06.007
[24]	Austin J, Schepelmann A, Geyer H. Control and evaluation of series elastic actuators with nonlinear rubber springs. In: Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Hamburg, Germany: IEEE, 2015. 6563-6568 http://www.mendeley.com/catalog/control-evaluation-series-elastic-actuators-nonlinear-rubber-springs/
[25]	Yu H Y, Huang S N, Chen G, Pan Y P, Guo Z. Human-robot interaction control of rehabilitation robots with series elastic actuators. IEEE Transactions on Robotics, 2015, 31(5):1089-1100 doi: 10.1109/TRO.2015.2457314
[26]	Garabini M, Passaglia A, Belo F, Salaris P, Bicchi A. Optimality principles in stiffness control: the VSA kick. In: Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA). Saint Paul, MN, USA: IEEE, 2012. 3341-3346 http://www.mendeley.com/catalog/optimality-principles-stiffness-control-vsa-kick/
[27]	Braun D J, Howard M, Vijayakumar S. Optimal variable stiffness control:formulation and application to explosive movement tasks. Autonomous Robots, 2012, 33(3):237-253 doi: 10.1007/s10514-012-9302-3
[28]	Lee J, Laffranchi M, Kashiri N, Tsagarakis N G, Caldwell D G. Model-free force tracking control of piezoelectric actuators: application to variable damping actuator. In: Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA). Hong Kong, China: IEEE, 2014. 2283-2289 http://www.mendeley.com/research/modelfree-force-tracking-control-piezoelectric-actuators-application-variable-damping-actuator/
[29]	Lee J, Jin M L, Tsagarakis N G, Caldwell D G. Terminal sliding-mode based force tracking control of piezoelectric actuators for variable physical damping system. In: Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Chicago, IL, USA: 2014. 2407-2413 http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6942889
[30]	Wang M, Sun L, Yin W, Dong S, Liu J T. A novel sliding mode control for series elastic actuator torque tracking with an extended disturbance observer. In: Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO). Zhuhai, China: IEEE, 2015. 2407-2412 http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7419699
[31]	Dupree K, Patre P M, Wilcox Z D, Dixon W E. Optimal control of uncertain nonlinear systems using RISE feedback. In: Proceedings of the 47th IEEE Conference on Decision and Control (CDC). Cancun, Mexico: IEEE, 2008. 2154-2159 http://www.mendeley.com/catalog/optimal-control-uncertain-nonlinear-systems-using-rise-feedback/
[32]	王萌, 孙雷, 尹伟, 董帅, 刘景泰.面向交互应用的串联弹性驱动器力矩控制方法.自动化学报, 2017, 43(8):1319-1328 http://www.aas.net.cn/CN/abstract/abstract19106.shtml Wang Meng, Sun Lei, Yin Wei, Dong Shuai, Liu Jing-Tai. Series elastic actuator torque control approach for interaction application. Actia Automatica Sinca, 2017, 43(8):1319-1328 http://www.aas.net.cn/CN/abstract/abstract19106.shtml

施引文献

期刊类型引用(22)

1.	张欣，张雁，张鑫. 基于亮度与彩色纹理统计的无参考图像评价. 信息技术与信息化. 2023(01): 122-129 . 百度学术
2.	何锦成，韩永成，张闻文，何伟基，陈钱. 基于通道校正卷积的真彩色微光图像增强. 兵工学报. 2023(06): 1643-1654 . 百度学术
3.	罗小燕，刘顺，汤文聪，王兴卫. 基于Mask RCNN的矿仓入料口堵塞矿石识别定位研究. 有色金属科学与工程. 2022(01): 101-107 . 百度学术
4.	陈健，李诗云，林丽，王猛，李佐勇. 模糊失真图像无参考质量评价综述. 自动化学报. 2022(03): 689-711 . 本站查看
5.	段添耀，柯圆圆. 基于多种颜色模型的马赛克瓷砖选色研究. 江汉大学学报(自然科学版). 2022(04): 45-52 . 百度学术
6.	来晓. 基于微调优化的深度学习在果蔬识别中的应用. 智能计算机与应用. 2021(04): 117-123 . 百度学术
7.	贺杰，王桂梅，刘杰辉，杨立洁. 基于图像处理的皮带机上煤量体积计量. 计量学报. 2020(12): 1516-1520 . 百度学术
8.	柴富杰，邓嘉敏，李建森，刘正发. 数码照相颜色数值与物质浓度辨识的数学模型. 数学的实践与认识. 2019(04): 305-311 . 百度学术
9.	陈扬，李旦，张建秋. 互补色小波域图像质量盲评价方法. 电子学报. 2019(04): 775-783 . 百度学术
10.	侯向宁，刘华春. 基于MSER和SVM以及强种子区域生长的车牌定位. 西安工程大学学报. 2019(02): 180-185 . 百度学术
11.	梁长江，吴雪梅，王芳，宋朱军，张富贵. 基于无人机的田间地膜识别算法研究. 浙江农业学报. 2019(06): 1005-1011 . 百度学术
12.	刘星星，王烁烁，徐丽明，袁全春，马帅，于畅畅，牛丛，陈晨，袁训腾，曾鉴. 基于OpenCV的动态葡萄干色泽实时识别. 农业工程学报. 2019(23): 177-184 . 百度学术
13.	李可，陈洪亮，张生伟，万锦锦. 基于SVM的雾天图像分类技术研究. 电光与控制. 2018(03): 37-41+47 . 百度学术
14.	丁丽. 基于粗集理论的车辆状态检测. 电脑知识与技术. 2018(01): 189-190+208 . 百度学术
15.	胡晓丽，钟昊，李彤. 基于二值图像连通域的甘蔗螟虫识别计数方法. 桂林电子科技大学学报. 2018(03): 210-214 . 百度学术
16.	张宪红，张春蕊. 基于六维前馈神经网络模型的图像增强算法. 山东大学学报(工学版). 2018(04): 10-19 . 百度学术
17.	李玉华，李天华，牛子孺，吴彦强，张智龙，侯加林. 基于色饱和度三维几何特征的马铃薯芽眼识别. 农业工程学报. 2018(24): 158-164 . 百度学术
18.	郑恩，林靖宇. 基于图像质量约束的无序图像关键帧提取. 计算机工程. 2017(11): 210-215 . 百度学术
19.	任荣梓，高航. 基于混沌置乱的分量融合图像加密压缩方法. 计算机技术与发展. 2017(08): 106-109+114 . 百度学术
20.	元朴康，况盛坤，王强，田全慧. 基于GRNN的模糊图像盲评价. 包装工程. 2016(13): 195-200 . 百度学术
21.	李俊峰，张之祥，沈军民. 基于亮度统计的无参考图像质量评价. 光电子·激光. 2016(10): 1101-1110 . 百度学术
22.	万泽慧. 试析网络图像的色彩管理要点. 无线互联科技. 2016(04): 32-34 . 百度学术