-
Abstract: RBF-AR (radial basis function network-based autoregressive) model is reconstructed as a new type of general radial basis function (RBF) neural network, which has additional linear output weight layer in comparison with the traditional three-layer RBF network. The extended Kalman filter (EKF) algorithm for RBF training has low filtering accuracy and divergence because of unknown prior knowledge, such as noise covariance and initial states. To overcome the drawback, the expectation maximization (EM) algorithm is used to estimate the covariance matrices of noises and the initial states. The proposed method, called the EM-EKF (expectation-maximization extended Kalman filter) algorithm, which combines the expectation maximization, extended Kalman filtering and smoothing process, is developed to estimate the parameters of the RBF-AR model, the initial conditions and the noise variances simultaneously. It is shown by the simulation tests that the EM-EKF method for the reconstructed RBF-AR network provides better results than structured nonlinear parameter optimization method (SNPOM) and the EKF, especially in low SNR (signal noise ratio). Moreover, the EM-EKF method can accurately estimate the noise variance. F test indicates there is significant difference between results obtained by the SNPOM and the EM-EKF.摘要: 为了利用EKF（extended Kalman filter）算法对RBF-AR（radial basis function network-based autoregressive）模型进行参数估计，重构了RBF-AR模型的网络结构，将其变换成一种新型的广义径向基函数（radial basis function，RBF）神经网络.与典型三层RBF网络结构相比，该广义RBF网络增加了线性输出加权层.为了克服基于EKF神经网络学习算法由于噪声统计特性未知导致滤波发散或者滤波精度不高的问题，利用EM（expectation maximization）算法对RBF-AR模型噪声协方差矩阵进行估计.同时，通过EKF滤波实时估计RBF-AR模型参数（系统状态），EKF平滑过程得到了更加准确的期望估计.仿真结果显示，该方法用在此变形的RBF-AR模型结构中是有效的，特别在信噪比低的情况下，估计效果比SNPOM（structured nonlinear parameter optimization method）方法好，而且还能估计出噪声方差.F检验显示了两方法估计得到的标准偏差有显著性差异.
-
在计算机视觉和模式识别领域, 输入数据的维数过高会增加计算的复杂度, 使得对数据的处理变得困难.为了降低数据的维数, 通常采用矩阵分解的方法.矩阵分解的方法将数据矩阵分解成多个矩阵的形式, 其中一个矩阵可以很好地逼近原始矩阵, 在保留原始信息的条件下, 同时可以从高维到低维的映射, 学习更好的特征描述方法.这样这种矩阵分解的方法有多种, 如SVD (Singular value decomposition)、QR分解、NMF (Nonnegative matrix factorization)等.
NMF可以将原始数据分解为基矩阵和系数矩阵的乘积.基矩阵的作用类似人脸的各个不同局部块的描述, 系数矩阵为原始数据在这些基向量的线性组合的权重.对于给定的数据矩阵$X$, 在学习到对应的基矩阵$U$之后, 对应的系数矩阵$V$便可以描述原始矩阵.最近的研究表明, NMF在人脑识别等领域已经超过基于SVD的方法[1-3].
虽然单视图的NMF提高了原始数据的有效性, 但是图像可以从不同的视图进行描述.这些视图可以是不同的数据集, 也可以是侧重于不同角度的特征提取方法, 所以, 这些视图具有多种特征:有的是视觉底层特征、有的是视觉美学特征, 甚至有中层语义特征.这些特征往往可以互补地描述图像[4], 因此, 多视图学习相比较于单视图的方法能更有效地利用视图之间的互补信息.而在实例检索[5]任务上, Multi的思想[6]也被用于获得更加精确的检索效果.目前, 利用多视图来进行聚类分析的方法主要有两种:多视图谱聚类和多视图K均值聚类.其中, 多视图谱聚类有文献[7-11]等.虽然这些方法性能的相比单视图的谱聚类有所提高, 但是多视图谱聚类需要为每一个视图都计算亲和矩阵, 视图越多, 计算的复杂度也更大.相比之下, 多视图K均值聚类不需要计算亲和矩阵, 只需要利用原始特征即可.多视图K均值聚类又分为基于指示矩阵的方法和基于NMF矩阵分解的方法.基于指示矩阵的方法有RMKMC[12]和DEKM (Discriminatively emmbedded K-means)[13]等, 这种方法是从样本角度来形成聚类质心, 且这种方法的准确率依赖于指示矩阵的初始值.而基于NMF矩阵分解的方法是从维数的角度来进行降维, 从而形成聚类质心.具体地, 关于矩阵分解多视图学习方面的研究有很多:在文献[14]中, Kumar等利用全局和局部2种视图的特征, 提高了单视图NMF在人脸识别问题上的准确率; 文献[15]利用稀疏编码框架来对多视图特征学习进行研究; 文献[16]中, Akata等提出Collective-NMF算法令多种特征数据共享相同的系数矩阵, 这等同于先串联各种特征然后进行NMF分解.然而Liu等认为这种共享系数矩阵具有太强的约束, 提出一种弱化的约束, 旨在保证每种特征的一致性, 即视角间的一致性保持[17].
但是, 以上这些方法没有考虑相同样本在不同视角中的空间结构关系, 这种局部空间结构在半监督学习、流形学习等多个领域的方法中具有重要的意义.典型的计算空间局部结构约束的方法有Locality preserving projection (LPP)[18]和Spectral Regression[19]等. Cai等在文献[19]的算法中, 通过引入局部结构约束达到了大幅度提高实验准确率的效果.
因此, 本文提出了一种基于局部结构约束的多视图特征学习方法, 称之为MultiGNMF.这种方法的主要目标是相似的数据在每个视图都有相近的相似性.因此, 我们通过构建亲和矩阵来将每个视图的空间结构加入到目标函数中, 并提出迭代规则来解决这个优化问题.然而, MultiGNMF等多视图学习方法要求特征矩阵的值是非负的, 而实际中并不能总是保证这一限制条件.为了消除这一限制条件, 本文又提出了一种基于多视图学习的MultiGSemiNMF算法.
文章主要结构分为4个部分:在第1节, 简要回顾一下基于矩阵分解的特征学习方法, 并将局部结构约束引入多视图学习框架中, 提出基于局部结构约束的多视图NMF分解算法—MultiGNMF; 在第2节, 针对MultiGNMF等多视图学习方法只适用于非负矩阵的缺点, 提出MultiGSemiNMF算法, 并对其进行详细介绍; 第3节对所提的算法进行实验验证和分析; 最后, 第4节对本文的工作进行总结.
1. 基于非负矩阵分解的特征学习方法及其存在问题
在这一节, 我们首先介绍基于NMF分解的单视图特征学习方法.然后, 考虑到多视图特征比单视图特征能更好地描述图像, 且分解后的系数矩阵应与原始特征据的空间结构相似, 我们提出了基于局部结构约束的多视图特征学习方法—MultiGNMF.下面将分别介绍NMF和MultiGNMF这两种特征学习算法.
1.1 NMF特征学习方法
下面介绍NMF的求解过程.
定义${X=[X_{\mathit{\boldsymbol{.}}, 1}, \cdots, X_{\mathit{\boldsymbol{.}}, N}] \in\, {\bf R}^{M\times N}}$为输入数据矩阵, 每一列都描述的是一个数据, ${U\in\, {\bf R}^{M\times K}}$为基矩阵, ${V\in\, {\bf R}^{N\times K}}$为系数矩阵, 即新的描述子, 两者的乘积是对原始矩阵的逼近, 如式(1)所示, 其中$K$是一个变量, 它决定了特征最终学习的特征维数.
$ \begin{equation} X\approx UV^\mathit{\boldsymbol{T}}, \qquad U\geq0, V\geq0, X\geq0 \end{equation} $
(1) 如果从每一列的视图来观察这个表达式, ${X_j\approx U{(V_{j, \mathit{\boldsymbol{.}}})}^{\rm T}=\sum_{k=1}^K {U_{\mathit{\boldsymbol{.}}, k} V_{j, k}}}$, $U_{\mathit{\boldsymbol{.}}, k}$表示矩阵的第$k$列, $V_{j, \mathit{\boldsymbol{.}}}$代表矩阵的第$j$行, 我们称这两个向量为基向量和系数向量.这样可以很清晰地看到, 一个样本数据($X$的列向量)是基矩阵的各个基向量($U_{{\rm .}, k}$)的线性累加了.度量矩阵分解的误差的方法有很多种, 在欧氏空间中一般采用$l_F$范数来度量矩阵之间的距离.这样整个NMF求解便变成如下的有约束优化问题.
$ \begin{equation} \min\limits_{U, V} {\parallel{X-UV^{\rm T}}\parallel}_{\rm F}^2, \qquad {\rm s.\, t.}\quad\, U\geq0, V\geq0 \end{equation} $
(2) 采用KKT (Karush-Kuhn-Tucher)条件, 分别引入拉格朗日因子$\Psi$和$\Phi$将$U\geq0, V\geq0$这两个约束条件变成无约束优化问题, 如式(3)所示.
$ \begin{equation} L={\parallel{X-UV^{\rm T}} \parallel}_{\rm F}^2 +{\rm tr}(\Psi U^{\rm T} )+{\rm tr}(\Phi V^{\rm T} ) \end{equation} $
(3) 对于同时满足$U$和$V$的条件下对于式(3)这种无约束优化问题是非凸优化问题, 没有精确的求解方法.文献[19]提出了乘子更新法则来迭代求解上述最小化约束问题.迭代过程如式(4)和(5)所示.
$ \begin{align*} \frac{\partial L}{\partial U}=\, &UV^{\rm T}V-XV+\Psi \Rightarrow \\ &U_{j, k}=U_{j, k}\times \frac {{(XV)}_{j, k}}{(UV^{\rm T}V)_{j, k}} \end{align*} $
(4) $ \begin{align*} \frac{\partial L}{\partial V}=\, &VU^{\rm T}U-X^{\rm T}U+\Phi \Rightarrow\\ & V_{j, k}=V_{j, k}\times \frac{{(X^{\rm T}U)}_{j, k}}{(VU^{\rm T}U)_{j, k}} \end{align*} $
(5) 1.2 MultiNMF特征学习方法
NMF是基于单视图的特征学习方法, 然而, 对同一个样本而言, 不同视图的多种特征往往可以互补地描述图像.基于此, 文献[17]提出了对每种特征保持弱化的一致性约束的多视图学习方法—MultiNMF.现将MultiNMF介绍如下.定义$X$为$G$个视图的输入特征数据矩阵, ${X^f=[X^f_{\mathit{\boldsymbol{.}}, 1}, \cdots, X^f_{\mathit{\boldsymbol{.}}, N}]\in {{\bf R}^{M_f\times N}}, (f\in {[1, G]}}$)为第$f$个视图的特征矩阵.其中, $M_f$为第$f$个视图的特征维数, $N$为样本数据的数量.对应地, 定义基矩阵${U={U^1, \cdots, U^G}}$和系数矩阵${V={V^1, \cdots, V^G }}$, ${U^f\in R^{M_f\times K}, V^f\in R^{N\times K}}$.其中, $K$为定义的新特征维数. Liu在文献[17]中提出Soft-regularization的方法认为, 对每个视图映射后的特征$V^f$需要保持一致性的约束, 但是允许存在差异性, 差异的大小采用欧氏空间中的$l_F$范数来度量.于是, 可以得到Liu的方法定义的损失函数如下式(6)所示.
$ \min\limits_{U^f, V^f, V^\ast}\sum\limits_{f=1}^G\parallel X^f-U^f{V^f}^{\rm T}\parallel_{\rm F}^2+\lambda_f{\parallel{V^f-V^\ast}\parallel}_{\rm F}^2\\ \quad {\rm s.t.}~\, X^f\geq0, U^f\geq0, V^f\geq0, V^\ast\geq0\\ \quad {\parallel{U_{\ast, k}^f}\parallel}_1=1, \, {k=1, \cdots, K}, \, {f=1, \cdots, G} $
(6) 方程的解需要采用乘子更新法则来进行迭代求得, 具体过程这里不再赘述.
1.3 MultiGNMF特征学习方法
局部空间结构约束的思想主要是保持样本的局部空间结构不变(近似不变), 这种局部空间结构在多个领域的方法中具有重要的意义.而MultiNMF没有考虑相同样本的原始数据与降维之后数据的空间结构关系, 因此, 本文提出了基于NMF矩阵分解的局部结构正则化约束多视图学习方法, 称之为MultiGNMF.下面对MultiGNMF方法进行详细介绍.
1.3.1 局部结构正则化约束
局部空间结构近似不变的具体含义就是:如果两个样本$x_i$和$x_j$在原始空间中相似, 那么我们认为它们在映射后的空间中(分别用$V_{i, \mathit{\boldsymbol{.}}}$和$V_{j, \mathit{\boldsymbol{.}}}$表示)也应该有近似的相似程度, 即原始数据与映射后的数据有相似的局部结构关系.
根据以往文献的考察, 我们采用数据的亲和矩阵$W$来表征局部结构关系.计算亲和矩阵的方法很多, 在没有监督信息的前提下, 一般采用数据之间的欧氏距离构建亲和矩阵$W$.定义一个正整数变量$k$, 一个样本$i$与其他样本的权重可以如此计算:对所有样本与该样本的距离进行从小到大的排序, 如果样本$j$在前$k$个, 那么$W_{ij}=1$; 否则, $W_{ij}=0$.还有其他的方法不采用0/1值作为权值, 而是直接用数据之间的核函数值作为权值.典型的核函数有高斯核$W_{ij}={\rm e}^\frac{-{\parallel{x_i-x_j}\parallel} ^2}{\sigma}$, 线性核$W_{ij}={x_i}^{\rm T} x_j$等.不同的计算方法适应于不同的研究内容, 在文档特征中采用线性核表现更好, 在图像视觉特征中高斯核可能更适合.在和其他的方法比较的过程中, 我们采用比较通用的高斯核函数值作为权值, 从而就可以得到原始数据的亲和矩阵$W$.但是, 这些方法的性能受参数的影响较大.最近, Nie等[20]提出了一种无参数构建亲和矩阵$W$的方法, 该方法不需要任何参数, 很好地解决了构图过程需要反复调节参数的问题.但本文提出的MultiGSemiNMF和MultiGNMF算法直接应用无参数构图后缺乏普适性, 因此本文仍然使用高斯核函数来构建亲和矩阵, 在以后的工作将深入研究无参数构图和本文方法的结合.对于经过映射后的数据$V_{i, \mathit{\boldsymbol{.}}}$和$V_{j, \mathit{\boldsymbol{, }}}$, 仍用欧氏距离来度量它们之间的相似程度, 如式(7)所示.利用亲和矩阵$W$, 我们便可以构造用于约束局部结构的平滑惩罚因子.对于第$f$个视图的平滑惩罚因子$R^f$, 公式如下:
$ \begin{equation} \mathcal {D}(V_{i, \mathit{\boldsymbol{.}}}, V_{j, \mathit{\boldsymbol{.}}} )={\parallel{V_{j, \mathit{\boldsymbol{.}}}^f-V_{i, \mathit{\boldsymbol{.}}}^f}\parallel}^2 \end{equation} $
(7) $ \begin{align*} R^f&=\sum\limits_{i, j=1}^N{\parallel{V_{j, \mathit{\boldsymbol{.}}}^f-V_{i, \mathit{\boldsymbol{.}}}^f }\parallel}^2 W_{ij}^f=\\ &{\rm tr}((V^f )^{\rm T} D^f V^f )-{\rm tr}((V^f )^{\rm T} W^f V^f )= \\ &{\rm tr}((V^f )^{\rm T} L^f V^f ) \end{align*} $
(8) 其中, $L=D-W$为拉普拉斯矩阵, $D$是一个对角矩阵$D_{(j, j)} =\sum_iW_{i, j} $.
1.3.2 目标方程的构建及求解
将平滑惩罚因子引入多视图特征学习MultiNMF的框架中, 我们得到MultiGNMF方法的目标函数如下:
$ \begin{align*} \min\limits_{U^f, V^f, V^\ast}\sum\limits_{f=1}^G&{\parallel{X^f-U^f{(V^f)}^{\rm T}}\parallel}_{\rm F}^2+\lambda_f{\parallel{V^f-V^\ast}\parallel}_{\rm F}^2+\\ & \mu\lambda_f {\rm tr}((V^f)^{\rm T}L^fV^f))\\ {\rm s.\, t.}~\, X^f\geq0,& U^f\geq0, V^f\geq0, V^\ast\geq0\\ &{\parallel{U_{\ast, k}^f}\parallel}_1=1, \, {k=1, \cdots, K}, \, {f=1, \cdots, G} \end{align*} $
(9) Liu在文献[17]中建议用对角阵$Q$归一化$U$和$V$, 即$UV^{\rm T}=UQ^{-1} QV^{\rm T}$.其中, $Q_f$定义如下:
$ \begin{equation} Q_f:= {\rm diag}{\left(\sum\limits_{m=1}^MU_{m, 1}^f, \cdots, \sum\limits_{m=1}^MU_{m, K}^f \right)} \end{equation} $
(10) diag$(\cdot)$表示对角矩阵.这样, 经过归一化后, ${\parallel{U_{*, i} \parallel}_1=1}$.因此, 式(9)可以改写成:
$ \begin{align*} \min\limits_{U^f, V^f, V^\ast}\sum\limits_{f=1}^G&{\parallel{X^f-U^f{(V^f)}^{\rm T}}\parallel}_{\rm F}^2+\lambda_f\parallel V^fQ^f-\\ &V^\ast\parallel_{\rm F}^2+\mu\lambda_f Tr((V^f)^{\rm T}L^fV^f))\\ {\rm s.\, t.}~\, &X^f\geq0, U^f\geq0, V^f\geq0, V^\ast\geq0 \end{align*} $
(11) 由此, 我们可以得到整体的损失函数定义如式(12)所示.
$ \begin{align*} L_G=\sum\limits_{f=1}^G&{\parallel{X^f-U^f{(V^f)}^{\rm T}}\parallel}_{\rm F}^2+\lambda_f\parallel V^fQ^f-\\ &V^\ast\parallel_{\rm F}^2+\mu\lambda_f {\rm tr}((V^f)^{\rm T}L^fV^f)) \end{align*} $
(12) MultiGNMF在$U^f\geq0, V^f\geq0$的约束下最小化$L_G$是一个带约束的优化问题.采用迭代的方法求解.引入拉格朗如因子后, MultiGNMF的第$f$种特征损失函数为式(13).
$ \begin{align*} L_1=\, &{\parallel{X-UV^{\rm T}} \parallel}_{\rm F}^2+\lambda_f{\parallel{VQ-V^\ast}\parallel}_{\rm F}^2+\\ &{\rm tr}(\Phi V^{\rm T} )+ \mu\lambda_f{\rm tr}(V^{\rm T}LV)+{\rm tr}(\Psi U^{\rm T} ) \end{align*} $
(13) $L_1$分别对$U$和$V$求导, 求导结果如下:
$ \begin{align*} \frac{\partial L_1}{\partial U}&=UV^{\rm T}V-XV+\Psi+\lambda_fP \\ \frac{\partial L_1}{\partial V}&=VU^{\rm T}U-X^{\rm T}U+\Phi+\lambda_f{(V-V^\ast+\mu LV)} \end{align*} $
(14) 其中, $P:={(\sum_{m=1}^MU_{m, k}\sum_{n=1}^NV_{n, k}^2-\sum_{n=1}^NV_{n, k}V_{n, k}^\ast)}$.采用KKT条件${\Psi_{j, k}U_{j, k}=0}$和${\Phi_{j, k}V_{j, k}=0}$得到$U$和$V$的迭代式如下:
$ \begin{eqnarray*} U_{j, k}\leftarrow U_{j, k}\times\frac{{(XV)}_{j, k}+\lambda_f \sum\limits_{n=1}^NV_{n, k}V_{n, k}^\ast}{{(UV^{\rm T}V)}_{j, k}+\lambda_f \sum\limits_{n=1}^NV_{n, k}^2}\\ V_{j, k}\leftarrow V_{j, k}\times\frac{{({X^{\rm T}U}+\lambda_fV^\ast+\mu\lambda_fWV)}_{j, k}}{{({VU^{\rm T}U}+\lambda_fV+\mu\lambda_fDV)}_{j, k}} \end{eqnarray*} $
(15) 根据文献[17], 我们在每次迭代得到$U$和$V$之后, 按照式(10)进行归一化处理, 即:
$ \begin{equation} U^f\leftarrow U^f{(Q^f)}^{-1}, \, V^f\leftarrow V^fQ^f \end{equation} $
(16) 在优化$U$和$V$之后, 将它们视为常量, 对$L_1$求导得到$V^\ast$的更新表达式如下所示:
$ \begin{equation} V^\ast=\dfrac{\sum\limits_{f=1}^G\lambda_fV^f}{\sum\limits_{f=1}^G\lambda_f} \end{equation} $
(17) NMF和MultiGNMF都要求$U\geq0, V\geq0, X\geq0$.这种非负性约束来源于在现实世界中大部分数据是非负的, 系数的累加也是非负的.然而, 实际情况中, 我们提取到的图像特征往往存在负数, 这就使得以上两种特征学习方法存在局限性.为了消除这个局限, 我们提出一种对负数特征也适用的多视图特征学习方法—ṀultiGSemiNMF, 我们将在下一节对其进行详细介绍.
2. MultiGSemiNMF特征学习方法
在第1节中我们分析了各种基于NMF矩阵分解的特征学习方法的优越表现, 不过这些方法有一个重要的约束:所有数据都必须是非负的.在物理世界中可能大部分数据保持这个特性, 但是, 在图像处理中有些特征, 如由小波变换得到的三分法特征、结构特征等, 并没有保持非负性的条件, 如果强制向正数方向映射, 往往含有一定的失真.这就使得基于NMF的特征学习方法有一定的局限性.如何将NMF算法拓展到对负数矩阵也适用, 文献[13]中进行了详细探究.其中一种方法是SemiNMF, 下面我们对其进行介绍, 并由此引出本文所提算法—ṀultiGSemiNMF.
2.1 SemiNMF特征学习方法
SemiNMF中的数据与NMF中的数据一致, 但是, SemiNMF算法对原始数据$X$和基矩阵$U$不带有非负性约束, 只需系数矩阵$V\geq0$.由此, 我们可以得到SemiNMF的目标方程和损失函数分别如式(18)和(19)所示:
$ \min\limits_{U, V} {\parallel{X-UV^{\rm T}}\parallel}_{\rm F}^2, \quad {\rm s.\, t.}\, V\geq0 $
(18) $ L_{semi}={\parallel{X-UV^{\rm T}}\parallel}_{\rm F}^2= \\ \ \ \ \ \ \ \ \ \ \ \ {\rm tr}{(XX^{\rm T}-2X^{\rm T}UV^{\rm T}+VU^{\rm T}UV^{\rm T})} $
(19) SemiNMF在$V\geq0$的约束下最小化$L_{semi}$是一个带约束的优化问题.采用迭代的方法求解, 求解过程我们将在第2.2节具体介绍.
2.2 MultiGSemiNMF特征学习方法
SemiNMF这种方法具有很好的描述性, 同时相对NMF有较大使用范围和较高性能.于是, 为了克服基于NMF的各种特征学习方法只适用于非负数据的缺点, 本文提出基于SemiNMF的多视图特征学习算法, 我们称之为MultiGSemiNMF.下面将对这种方法做详细的介绍.
2.2.1 目标方程
多视图学习过程中我们需要遵守几个准则: 1)每个视图学习的新特征需要保持一致性; 2)在学习前的特征和学习后的特征对样本之间的局部结构进行度量, 需要保持这种结构的一致性.于是, 我们得到弱化的一致性约束项${{\parallel V^f-V^\ast \parallel}_{\rm F}^2}$和局部结构正则化约束项${{\rm tr}((V^f )^{\rm T}L^f V^f)}$.我们将多视图学习的准则应用到SemiNMF, 于是, 我们可以得到MultiGSemiNMF算法的目标函数如式(20)所示.
$ \begin{align*} \min\limits_{U^f, V^f, V^\ast}\sum\limits_{f=1}^G&{\parallel{X^f-U^f{(V^f)}^{\rm T}}\parallel}_{\rm F}^2+\lambda_f\parallel V^fQ^f-\\ &V^\ast\parallel_{\rm F}^2+\mu\lambda_f {\rm tr}((V^f)^{\rm T}L^fV^f))\\ \quad {\rm s.t.}\quad &V^f\geq0, V^\ast\geq0 \end{align*} $
(20) 其中, $Q^f$的引进是为了使方程满足${{\parallel{U_{\ast, k}^f}\parallel}_1=1}$的约束条件.而${{\parallel{U_{\ast, k}^f}\parallel}_1=1}$的约束条件是为了每一种特征的数据归一化处理, 那么对应的系数矩阵也变得归一化, 具有比较性.又因为${\parallel X\parallel}={\parallel \sum_jX_j\parallel} \approx \sum_{k=1}^K{\parallel {U_{i, k}\sum_jV_{j, k}}}\parallel =\sum_{k=1}^K{\parallel {\sum_jV_{j, k}\parallel}}= \parallel V\parallel$.所以, 在$U$归一化之后如果对$X$也进行归一化处理, $V$便也达到归一化的目的.而$X$为原始数据我们能更好的操作, 故在求解过程中只需要在每次迭代$U$之后对其进行归一化即可.所以, 式(20)可以简写成(21), 但是我们需要求解前对原始数据$X$进行归一化操作, 在每次迭代后对$U$进行归一化.
$ \begin{align*} \min\limits_{U^f, V^f, V^\ast}\sum\limits_{f=1}^G&{\parallel{X^f-U^f{(V^f)}^{\rm T}}\parallel}_{\rm F}^2+\lambda_f\parallel{V^fQ^f-}\\ &V^\ast\parallel_{\rm F}^2+\mu\lambda_f {\rm tr}((V^f)^{\rm T}L^fV^f)\\ \quad {\rm s.\, t.}\quad &V^f\geq0, V^\ast\geq0 \end{align*} $
(21) 由此, 我们可以得到MultiGSemiNMF算法的整体损失函数如下所示:
$ \begin{align*} L_{GSemi}=\sum\limits_{f=1}^G&{\parallel{X^f-U^f{(V^f)}^{\rm T}}\parallel}_{\rm F}^2+\lambda_f\parallel{V^f-}\\ &V^\ast\parallel_{\rm F}^2+\mu\lambda_f {\rm tr}((V^f)^{\rm T}L^fV^f)) \end{align*} $
(22) 其中, $L=D-W$为拉普拉斯矩阵, $D$是一个对角矩阵${D_{(j, j) }=\sum_iW_{i, j}}$, $W$为样本在原始空间关系的亲和矩阵.各变量的具体含义及计算方法详见第1.3节.
2.2.2 方程求解
MultiGSemiNMF在${V^f\geq0}$的约束下最小化$L_{GSemi}$是一个带约束的优化问题.对于每个视图的特征, 引入拉格朗日因子后, MultiGSemiNMF的第$f$个视图特征的损失函数为
$ \begin{align*} L_2=&{\parallel{X-UV^{\rm T}} \parallel}_{\rm F}^2+\lambda_f{\parallel{V-V^\ast}\parallel}_{\rm F}^2+\\ &{\rm tr}(\Phi V^{\rm T} )+ \mu\lambda_f{\rm tr}(V^{\rm T}LV) \end{align*} $
(23) 损失函数在变量$U$和$V$下不是一个凸优化问题没有精确的数值解, 采用迭代优化方法求解, 具体计算步骤如下:
1) 对$V$取随机矩阵或者采用K-means算法得到的系数矩阵.
2) 固定$V$更新$U$.将$L_2$中只有变量$U$, 变成一个无约束优化问题, 对其求导${\frac{\partial L_2}{\partial U}=UV^{\rm T}V-XV=0}$, 获得$U$的解析解.其中${V^T V\in {\bf R}^{K\times K}}$在一般情况下是一个半正定的矩阵, 在不可逆的情况下, 用伪逆矩阵来代替(Matlab中的pinv函数).
$ \begin{equation} U=XV{(V^{\rm T}V)}^{-1} \end{equation} $
(24) 3) 固定$U$更新$V$.将$U$固定, $L_2$中只有变量$V$, 对其求导${\frac{\partial L_2}{\partial V}=VU^{\rm T}U-X^{\rm T}U+\Phi+\lambda_f{(V-V^\ast+\mu LV)}}$ ${=0}$, 采用KKT条件$\Phi_{j, k}V_{j, k}=0$获得式(25)的优化问题.
$ \begin{align*} &{(VU^{\rm T}U-X^{\rm T}U+\lambda_f(V-V^\ast+\mu LV))}_{ik}V_{ik}=\\ &\qquad\beta_{ik}V_{ik}=0 \end{align*} $
(25) 式(25)是一个典型的定点等式问题, 求解${f(x)=0}$, 可以变成${x=g(x)}$的形式, 迭代式子$x_{i+1}=g{(x_i)}$由于存在$V\geq0$的约束条件, 式(25)中的各项需要保持绝对的非负性.所以, 我们采用拆分的方法.通过拆分, ${X^{\rm T}U={(X^{\rm T}U)}^+-{(X^{\rm T}U)}^-, U^{\rm T}U={(U^{\rm T}U)}^+}$ ${-{(U^{\rm T} U)}^-}$, 其中的拆分函数定义如式(26)所示.这样式(25)便变成多个非负矩阵之间的线性组合.
$ \begin{equation} A_{ik}^+=\frac {\mid{A_{ik}\mid}+A_{ik}}{2}, \, A_{ik}^-=\frac {\mid{A_{ik}\mid}-A_{ik}}{2} \end{equation} $
(26) $ V_{ik}=V_{ik}\times \\ {\sqrt{\frac {{X^{\rm T}U}_{j, k}^++{[V{(U^{\rm T}U)}^-]}_{j, k}+\lambda_f{(\mu WV+V^\ast)}_{j, k}}{{X^{\rm T}U}_{j, k}^-+{[V{(U^{\rm T}U)}^+]}_{j, k}+\lambda_f{(\mu WV+V)}_{j, k}}}} $
(27) 文献[21]提出一种满足定点等式的${x=g(x)}$形式, 将式(27)所示, 代入到式(25)中${{(VU^{\rm T}U-X^{\rm T}U+\lambda_f(V-V^\ast+\mu LV))}_{ik}V_{ik} =0}$, 由于KKT条件约束${\beta_{ik}V_{ik}=0}$, 当${V_{ik}\neq0}$时, 必然存在$(VU^{\rm T}U-X^{\rm T}U+\lambda_f(V-V^\ast+\mu LV))_{ik} =0$, 式(27)满足式(25);反之, 当$V_{ik}=0$也满足.综合考虑, 式(27)满足KKT条件.迭代式(27)的收敛性证明方法可以详见文献[21-22].
4) 交替迭代第2)步和第3)步, 直到损失函数值小于阈值或损失函数值变化小于阈值.
5) 在优化$U$和$V$之后, 将它们视为常量, 利用式(17)更新${V^\ast}$. MultiGSemiNMF与MultiGNMF的不同之处在于缺少了${U^f\geq0}$的约束, 因此不仅适用于特征矩阵非负的情况, 在特征矩阵中存在负数时, 也表现良好.式(28)是各种变量的迭代方程.
$ \ \ \ U_{j, k}\leftarrow U_{j, k}\times\frac{{(XV)}_{j, k}+\lambda_f \sum\limits_{n=1}^NV_{n, k}V_{n, k}^\ast}{{(UV^{\rm T}V)}_{j, k}+\lambda_f \sum\limits_{n=1}^NV_{n, k}^2}\\ V_{ik}\leftarrow V_{ik}\times \\ {\sqrt{\frac {{X^{\rm T}U}_{j, k}^++{[V{(U^{\rm T}U)}^-]}_{j, k}+\lambda_f{(\mu WV+V^\ast)}_{j, k}}{{X^{\rm T}U}_{j, k}^-+{[V{(U^{\rm T}U)}^+]}_{j, k}+\lambda_f{(\mu WV+V)}_{j, k}}}} $
(28) 3. 实验设计与分析
为了验证MultiGNMF算法和MultiGSemiNMF算法的有效性, 我们在4个公共的图像数据库中和其他几种多特征学习算法比较图像聚类效果.下面分别从实验设置、评估指标和实验结果及分析这三部分作详细介绍.
3.1 实验设置
3.1.1 数据库
实验中所用的数据库为CMU PIE人脸数据库、UCI手写体数字图像数据库、3-Sources文本数据库和ORL人脸库.表 1详细介绍这4个数据库的统计特性.具体介绍如下:
表 1 4个数据库的资料Table 1 The information of four databases数据库 数量 视图个数 聚类个数 CMU PIE 2 856 2 68 UCI Digit 2 000 2 10 3-Sources 169 3 6 ORL 400 2 40 CMU PIE人脸数据库包含41 368张$32\times 32$像素的人脸图像, 这些数据是68个人按照指定的13种姿势角度和43种不同光照条件下采集人脸的图像.在实验中, 我们从每个人的一个角度中随机选择42幅图像, 构成2 856幅人脸图像.如果按照人脸作为聚类中心的话, 那么数据可以分成68个集群.在本次实验中, 我们用图像的像素值(二维图像按行展开)和HOG (Histogram of oriented gradient)特征作为CMU PIE的两个视图.
UCI手写体数字数据库有UCI大学构建数字0$\, \sim\, $ 9的手写体图像, 数据库包含2 000个样本.我们利用手写体图像的低频傅里叶变换和原始像素值作为不同的视图.
3-Sources文本数据库包含BBC、Reuters和Guardian三种流行的网上新闻资源.其中, 有169条新闻被这三个新闻网报道过.我们选取这169条新闻作为测试样本, 这三个新闻网分别作为三个视图来进行聚类分析.这些新闻的主题包含商业、娱乐、健康、政治、运动和科技, 我们将其作为我们聚类的标签.
ORL (Olivetti research laboratory)人脸库是英国剑桥大学Olivetti研究所制作的人脸数据库, 它共包含400张的人脸图像.这些数据是40个人在不同的时间、变化的光线、面部表情(张开/合拢眼睛、微笑/不微笑)和面部细节(戴眼镜/不戴眼镜)下拍摄的.所有的图像为实验者的正脸, 带有一定程度的朝上下左右的偏转或倾斜, 相似的黑暗同质背景.所有图像的大小均为$28\times 23$像素.在本次实验中, 我们用图像的像素值(二维图像按行展开)和低频傅里叶变换系数值作为ORL的两个视图.
3.1.2 对比算法
为了更全面地评估本文提出的算法, 我们比较了近期多种典型的多视图学习算法.下面对它们进行描述.
1) 单视图算法(BSV和WSV):我们对每个视图利用NMF算法进行特征学习, 将学习的系数矩阵作为特征.统计每个视图的效果, 我们取每个视图该算法对应的最好效果为BSV和最差效果为WSV.
2) ConcatNMF:这是一种前向融合的学习方法.其算法可以简单理解为, 首先将每个视图的特征串联成一个向量(矩阵)作为数据新的特征, 然后利用非负矩阵分解算法进行特征学习, 所有算法流程和度量标准与单视图的方法一致.
3) ColNMF:一种多视图学习方法, 采用一致性准则, 如式(29)所示, 所有的视图共享相同的系数矩阵.与ConcatNMF类似, 不过每个视图添加了权重和归一化约束.
$ \begin{equation} \min\limits_{U^f, V}\sum\limits_{f=1}^G{\parallel {X^f-U^f{(V)}^{\rm T}}\parallel}_{\rm F}^2 \end{equation} $
(29) 4) Co-reguSC:一种改进的谱聚类算法, 在文献[23]中被Kumar等提出.每个视图采用谱聚类学习作为基本的聚类学习算法, 与MultiNMF算法相似的是, 在视图之间采用弱一致性准则约束各个视图的映射矩阵之间的关系, 如式(30)所示.在实验中我们采用高斯核核函数, 该算法的详细介绍可以参考文献[23].
$ \begin{align} &\max\limits_{U^v, U^\ast}\sum\limits_{v=1}^m{\rm tr}{((U^v )^{\rm T}L^v U^v)}+\nonumber\\ &\qquad\sum\limits_v\alpha_v{\rm tr}{(U^v{(U^v)}^{\rm T}U^\ast {(U^\ast)}^{\rm T})} \end{align} $
(30) 5) MultiNMF:本文算法的基准算法, 采用弱一致性约束的多视图NMF学习方法.
6) Sc-ML:是一种改进的Co-reguSC算法. Dong等在文献[24]中提出, 利用格拉斯曼流行距离中的一种投影距离来定义不同视图学习的子空间之间一致性准则.
7) MMSC:是一种多模态的谱聚类方法.不同的模态(也就是图像特征)共享一个相同的图拉普拉斯矩阵, 也就是最后的聚类指示矩阵$G$.该算法的详细介绍可以参考文献[10].
$ \begin{align} &\min\limits_{G\geq0, G^{\rm T}G=I, G_i}\sum\limits_i({\rm tr}(G^i)^{\rm T}L^i G^i+\nonumber\\ &\qquad\alpha {\rm tr}{(G-G^i)}^{\rm T}\times(G-G^i)) \end{align} $
(31) 8) AMGL:是一种多视图谱聚类方法.但是不同视图所占的权重是自动学得的, 不需要有额外的参数来指导训练.该算法的详细介绍可以参考文献[11].
3.2 评估指标
本文采用以往文献中的经典评估方法: AC (精确度)和NMI (归一化互信息)来度量图像数据聚类的评估指标.给定一幅图像, 定义为图像的标签类别, 为图像对应的聚类中心的类别标签, AC可以用如下式(31)来定义.其中$n$为所有的测试图像数量, 是一个脉冲函数, 函数中两个参数相同则返回1, 否则返回0.是一种将聚类中心的标签映射到图像集已知的对等标签, 其中我们采用Kuhn-Munkres[25]的映射方法.
$ \begin{equation} AC=\frac {\sum\limits_{i=1}^n\delta{(\alpha_i, map(l_i))}}{n} \end{equation} $
(31) 给定两个数据集的所有聚类中心, 它们之间的互信息可以用式(32)计算.
$ \begin{equation} MI{(\mathcal {C}, \mathcal {C}')} = \sum\limits_{c_i \in \mathcal {C}, {c_j}'\in {\mathcal {C}'}}p{(c_i, c_j')}\cdot {\rm log}_2{\frac {p{(c_i, c_j')}}{p(c_i )p(c_j')}} \end{equation} $
(32) 其中, $p(c_i)$和${p(c_j' )}$表示在所有测试图像中被分到各自对应聚类中心的概率, 在这里我们用数量比率代表概率, ${p(c_i, c_j')}$表示一个图像被同时分到这两个聚类中心$c_i$和${c_j'}$的概率, 同样我们用数量比代替概率(注意在这里聚类算法计算得到的聚类中心的编号可以为任意的顺序).在实验中, 第一个聚类中心集为图像的已知类别标签, 同一个标签的图像为一个聚类中心, 第二个聚类中心集为聚类算法得到的标签, 标签可以为任意的顺序标签.归一化的互信息为互信息除以最大的聚类标签熵, 其中${H(\mathcal {C})=-\sum_ip(c_i) {\rm log}_2p(c_i)}$, ${p(c_i)}$指属于聚类中心${c_i}$的图像数量比率.
$ \begin{equation} NMI(\mathcal {C}, \mathcal {C}')=\frac {MI(\mathcal {C}, \mathcal {C}' )}{\max(H({\mathcal {C}}), H(\mathcal {C}' ))} \end{equation} $
(33) 3.3 实验结果与分析
3.3.1 聚类的准确性验证
在本文提出的方法需要计算各个数据之间的局部结构关系, 我们采用高斯核函数值作为权值, 即${W_{ij}={\rm e}^{-\frac {\parallel {x_i-x_j} \parallel ^2} {\sigma }}}$.变量${k=5}$, 这种参数设置在非大量样本数据库中使用的较多.在式(12)中所有的变量我们设定为${\lambda_f=0.01\, (f=1, \cdots, G), \mu =10}$, 与算法MultiNMF和MultiGNMF保持一致.
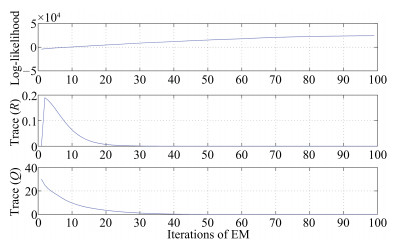
在定义了参数之后, 计算每个视图图像之间的亲和矩阵, 每种方法我们都运行20次, 取所有次数运行结果的平均值和方差作为最终的算法效果评估值.经过20次的实验运行, 我们统计了各种算法在4个数据库上的AC和NMI值, 如表 2和表 3所示.
表 2 不同方法在4个数据库中的AC值Table 2 The AC values by different methods in four databases算法 UCI Digit CMU PIE 3-Sources ORL BSV ${68.5\pm.05}$ ${55.2\pm.02}$ ${60.8\pm.01}$ ${51.8\pm.02}$ WSV ${63.4\pm.04}$ ${47.6\pm.01}$ ${49.1\pm.03}$ ${42.8\pm.05}$ ConcatNMF ${67.8\pm.06}$ ${51.5\pm.00}$ ${58.6\pm.03}$ ${66.8\pm.02}$ ColNMF ${66.0\pm.05}$ ${56.3\pm.00}$ ${61.3\pm.02}$ ${66.3\pm.04}$ Co-reguSC ${86.6\pm.00}$ ${59.5\pm.02}$ ${47.8\pm.01}$ ${70.5\pm.02}$ MultiNMF ${88.1\pm.01}$ ${64.8\pm.02}$ ${68.4\pm.06}$ ${67.3\pm.03}$ SC-ML ${88.1\pm.00}$ ${72.3\pm.00}$ ${54.0\pm.00}$ ${70.8\pm.00}$ MMSC ${89.4\pm.38}$ ${61.6\pm.06}$ ${69.9\pm.04}$ ${70.7\pm.06}$ AMGL ${82.6\pm.74}$ ${63.6\pm.19}$ ${68.3\pm.12}$ ${64.2\pm.10}$ MultiGNMF ${95.1\pm.10}$ ${72.5\pm.02}$ ${73.4\pm.00}$ ${73.5\pm.00}$ MultiGSemiNMF ${95.6\pm.02}$ ${77.2\pm.12}$ ${79.3\pm.00}$ ${76.2\pm.00}$ 表 3 不同方法在4个数据库中的NMI值Table 3 The NMI values by different methods in four databases算法 UCI Digit CMU PIE 3-Sources ORL BSV ${63.4\pm.03}$ ${74.1\pm.00}$ ${53.0\pm.01}$ ${69.8\pm.01}$ WSV ${60.3\pm.03}$ ${69.1\pm.02}$ ${44.1\pm.02}$ ${65.4\pm.04}$ ConcatNMF ${60.3\pm.03}$ ${70.5\pm.00}$ ${51.7\pm.03}$ ${85.1\pm.01}$ ColNMF ${62.1\pm.03}$ ${68.3\pm.00}$ ${55.2\pm.02}$ ${84.5\pm.03}$ Co-reguSC ${77.0\pm.00}$ ${80.5\pm.01}$ ${41.4\pm.01}$ ${80.5\pm.01}$ MultiNMF ${80.4\pm.01}$ ${82.2\pm.02}$ ${60.2\pm.06}$ ${87.6\pm.01}$ SC-ML ${87.6\pm.00}$ ${85.1\pm.00}$ ${45.5\pm.00}$ ${85.3\pm.00}$ MMSC ${88.0\pm.05}$ ${80.3\pm.01}$ ${66.3\pm.09}$ ${85.9\pm.01}$ AMGL ${84.9\pm.33}$ ${81.8\pm.10}$ ${56.9\pm.11}$ ${81.9\pm.02}$ MultiGNMF ${90.1\pm.04}$ ${90.2\pm.01}$ ${65.4\pm.00}$ ${88.5\pm.00}$ MultiGSemiNMF ${91.2\pm.01}$ ${93.8\pm.05}$ ${73.4\pm.00}$ ${89.9\pm.00}$ 在表 2和表 3中我们可以看到本文提出的算法在聚类分析中相比较其他多视图学习算法在准确度和归一化互信息两个指标下都有较好的表现.同时我们注意到Co-reguSC和SC-ML算法也采用了局部结构约束的条件(谱聚类算法是一种基于数据样本图结构的算法), MMSC也采用了一致性约束, 本文算法同样超过该类算法.在比较本文提出的算法MultiGSemiNMF和MultiGNMF算法中, 我们发现基于MultiGSemiNMF的算法相对于MultiGNMF算法聚类效果上也有提升, 即使所有特征并没有负数或零, 这证明在特征学习中MultiGSemiNMF算法比MultiGNMF算法在一些应用场景中具有更好的表现, 且MultiGSemiNMF消除了MultiGNMF算法要求所有特征非负的限制, 因此也有着更为广阔的应用平台.
3.3.2 参数对算法性能的影响
在式(12)中有$G$个参数变量$\lambda_f$, 它的物理意义是不同视图对学习过程的重要性进行权衡.如果我们具有一些先验知识, 带有噪声的视图特征可以适当减少权重, 被认为重要的视图如文本标签信息等可以适当增加权重.在我们的实验中没有先验知识, 同时数据已经归一化处理, 所以所有的$\lambda_f$定义为相同的数.但是$\lambda_f$的大小会影响聚类效果, $\lambda_f$越小则对系数矩阵的一致性约束越松弛, 反之, $\lambda_f$为无穷大的话所有系数矩阵为相同的数值.
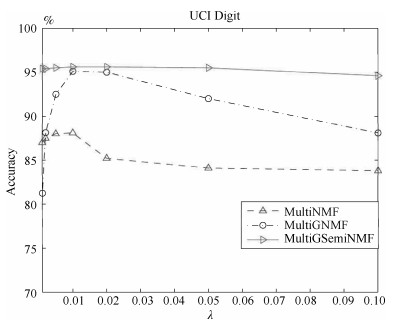
下面我们在两个数据库CMU PIE和UCI Digit上用MultiNMF、MultiGNMF和MultiSemiNMF三个算法做聚类分析, 准确率AC作为指标度量不同的$\lambda_f$值对实验的影响.我们设定$\lambda_f$为0.001, 0.005, 0.002, 0.01, 0.02, 0.05, 0.1, 图 1和图 2描述了对应的聚类效果.
图 1 在UCI Digit数据库中参数$\lambda$对本文算法的影响Fig. 1 The influences of $\lambda$ on UCI Digit database
图 2 在CMU PIE数据库中参数$\lambda$对本文算法的影响Fig. 2 The influences of $\lambda$ on CMU PIE database从图 1和图 2中我们可以看到, 在MultiNMF、MultiGNMF和MultiSemiNMF三个算法中, MultiGSemiNMF算法的准确率最高, 且受参数影响很小, 在较小或者较大的值均能有稳定的表现. MultiGNMF算法最不稳定, 但是在大部分实验中仍能超过基准算法MultiNMF.三种算法均在${\lambda=0.01}$时有较高的表现.
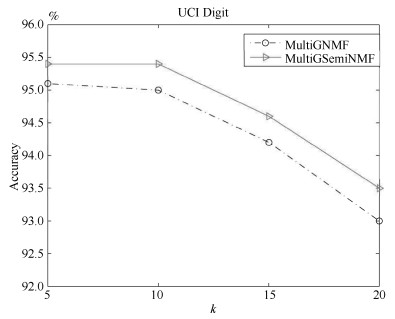
本文提出的算法MultiGSemiNMF和MultiGNMF需要构建一个样本亲和矩阵, 在损失函数其中有一个参数$k$, $k$值越大样本的局部结构约束越多, 反之局部结构约束越少.不同的$k$值对聚类效果有一定影响, 在与其他算法的比较中, 我们采用其他算法一样的$k$值, 在这里我们另外分析$k$值对本文提出算法的影响.在UCI Digit数据总库, 我们选取${k = 5, 10, 15, 20}$构建亲和矩阵(${\lambda=0.01}$), 用聚类的准确率AC来评估算法效果, 如图 3所示.
从图 3我们看到参数$k$对本文算法有一定的影响, $k$值越大虽然能更充分地保留样本之间的局部空间结构关系, 但是从图中的结果来看聚类准确度随着$k$的变大有降低的趋势.过度的保留空间结构关系并不能提升算法的效果, 反而可能产生过度拟合的副作用, 因为样本的结构关系是基于原始特征的距离计算得到, 而原始特征并不能充分描述样本信息, 其中或多或少含有冗余和噪声.同时, 也可以看出, 无论参数$k$取何值时, MultiGSemiNMF算法的性能都优于MultiGNMF算法.
4. 总结
本文提出了两种多视图学习的方法: MultiGNMF算法和MultiGSemiNMF算法. MultiGNMF和MultiGSemiNMF算法都是基于样本局部结构空间约束的非负矩阵分解多视图学习方法.
本文首先介绍了一种单视图学习方法: NMF矩阵分解.然后, NMF算法的基础之上, 在以往多视图学习的框架准则下, 本文提出了基于样本局部结构空间约束的非负矩阵分解多视图学习方法MultiGNMF.但是, MultiGNMF方法只适用于非负的特征矩阵. MultiGSemiNMF算法则不限于此.
为了验证本文提出的多视图学习算法的性能, 我们在公有的图像数据库中做聚类分析.实验中和以往的算法比较, 实验结果表明本文提出的算法相对于其他基于矩阵分解的多视图学习方法有更好的表现.同时实验中分析了算法中的参数变化对算法性能的影响, 实验结果表明MultiGSemiNMF对参数变化具有很好的鲁棒性.在未来的工作中, 我们将探索一种新的基于局部结构约束的多视图学习方法.
-
Fig. 3 The convergence process of the Log-likelihood, the measurement and process noise variance.
Fig. 5 The convergence process of the Log-likelihood, the measurement and process noise variance.
Fig. 6 The convergence process of the Log-likelihood, the measurement and process noise variance.
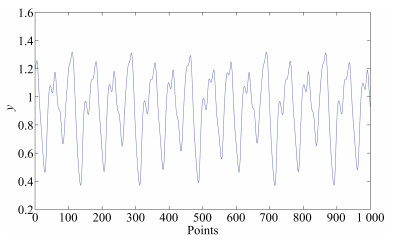
Table Ⅰ COMPARISON RESULTS FOR MACKEY-GLASS TIME SERIES
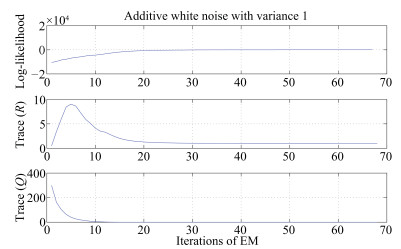
Method MSE (Training) MSE (Testing) $R$ SNPOM 1.0800E-7 1.2600E-7 unknown EKF 1.9560E-7 2.1786E-7 0.002 (given) EKF 1.2559E-7 1.9793E-7 0.0002 (given) EM-EKF 7.1765E-8 1.2008E-7 1.8146E-7 
下载: 导出CSV
Table Ⅱ COMPARISON RESULTS FOR MACKEY-GLASS TIME SERIES CORRUPTES BY ADDITIVE WHITE NOISE
Noise variance Method MSE (Training) MSE (Testing) R 0.25 SNPOM 0.26606 0.28120 unknown EKF 0.26577 0.28082 0.2 (given) EKF 0.27343 0.28825 0.1 (given) EM-EKF 0.25750 0.27825 0.25950 1 SNPOM 0.97452 1.1644 unknown EKF 0.97215 1.1512 0.8 (given) EKF 0.98262 1.1785 0.6 (given) EM-EKF 0.96590 1.13907 1.0589
下载: 导出CSV
Table Ⅲ THE RESULTS OF STATISTICAL F TEST AT LEVEL 0.05
Case $F_{\alpha=0.05}$ $F$ Results Case 1 (Training) 1.16 1.4642 Reject; Difference Case 1 (Testing) 1.16 1.0105 No reject; No difference Case 2 (Training) 1.16 14.1212 Reject; Significant difference Case 2 (Testing) 1.16 9.2984 Reject; Significant difference Case 3 (Training) 1.16 37.8297 Reject; Significant difference Case 3 (Testing) 1.16 15.5751 Reject; Significant difference
下载: 导出CSV
Table Ⅳ THE COMPUTATION TIME OF DIFFERENT METHODS (S)
Method Time SNPOM 10.690 EKF 0.40572 EM-EKF 30.766
下载: 导出CSV
-
[1] Z. Y. Shi, Y. Tamura, and T. Ozaki, "Nonlinear time series modelling with the radial basis function-based state-dependent autoregressive model, "Int. J. Syst. Sci. , vol. 30, no. 7, pp. 717-727, Jul. 1999. doi: 10.1080/002077299292038 [2] H. Peng, T. Ozaki, V. Haggan-Ozaki, and Y. Toyoda, "A parameter optimization method for radial basis function type models, "IEEE Trans. Neural Netw. , vol. 14, no. 2, pp. 432-438, Mar. 2003. http://europepmc.org/abstract/MED/18238025 [3] M. Gan, H. Peng, X. Y. Peng, X. H. Chen, and G. Inoussa, "A locally linear RBF network-based state-dependent AR model for nonlinear time series modeling, "Inform. Sci. , vol. 180, no. 22, pp. 4370-4380, Nov. 2010. http://www.sciencedirect.com/science/article/pii/S0020025510003300 [4] M. Gan, C. L. P. Chen, H. X. Li, and L. Chen, "Gradient radial basis function based varying-coefficient Autoregressive model for nonlinear and nonstationary time series, "IEEE Signal Proc. Lett. , vol. 22, no. 7, pp. 809-812, Jul. 2015. http://ieeexplore.ieee.org/document/6953131/ [5] H. Peng, J. Wu, G. Inoussa, Q. L. Deng, and K. Nakano, "Nonlinear system modeling and predictive control using the RBF nets-based quasi-linear ARX model, "Control Eng. Pract. , vol. 17, no. 1, pp. 59-66, Jan. 2009. http://www.sciencedirect.com/science/article/pii/S0967066108000993 [6] H. Peng, G. Kitagawa, J. Wu, and K. Ohtsu, "Multivariable RBF-ARX model-based robust MPC approach and application to thermal power plant, "Appl. Math. Model. , vol. 35, no. 7, pp. 3541-3551, Jul. 2011. http://www.sciencedirect.com/science/article/pii/S0307904X11000151 [7] M. Gan, H. Peng, and L. Y. Chen, "A global-local optimization approach to parameter estimation of RBF-type models, "Inform. Sci. , vol. 197, pp. 144-160, Aug. 2012. http://www.sciencedirect.com/science/article/pii/S0020025512000679 [8] M. Gan, H. X. Li, and H. Peng, "A variable projection approach for efficient estimation of RBF-ARX model, "IEEE Trans. Cybern. , vol. 45, no. 3, pp. 462-471, Mar. 2015. http://europepmc.org/abstract/med/24988599 [9] H. K. Wei and S. I. Amari, "Dynamics of learning near singularities in radial basis function networks, "Neural Netw. , vol. 21, no. 7, pp. 989-1005, Sep. 2008. http://dl.acm.org/citation.cfm?id=1411874 [10] J. S. Kim and S. Jung, "Implementation of the RBF neural chip with the back-propagation algorithm for on-line learning, "Appl. Soft Comput. , vol. 29, pp. 233-244, Apr. 2015. http://www.sciencedirect.com/science/article/pii/S1568494614006620 [11] F. P. Härter and H. F. de Campos Velho, "New approach to applying neural network in nonlinear dynamic model, "Appl. Math. Model. , vol. 32, no. 12, pp. 2621-2633, Dec. 2008. http://www.sciencedirect.com/science/article/pii/S0307904X07002296 [12] H. Z. Yang, J. Li, and F. Ding, "A neural network learning algorithm of chemical process modeling based on the extended Kalman filter, "Neurocomputing, vol. 70, no. 4-6, pp. 625-632, Jan. 2007. http://dl.acm.org/citation.cfm?id=1224059&CFID=448466066&CFTOKEN=67010250 [13] K. Salahshoor, S. Zakeri, and M. H. Sefat, "Stabilization of gas-lift oil wells by a nonlinear model predictive control scheme based on adaptive neural network models, "Eng. Appl. Artif. Intel. , vol. 26, no. 8, pp. 1902-1910, Sep. 2013. http://dl.acm.org/citation.cfm?id=2508322 [14] N. Y. Zeng, Z. D. Wang, Y. R. Li, M. Du, and X. H. Liu, "Inference of nonlinear state-space models for sandwich-type lateral flow immunoassay using extended Kalman filtering, "IEEE Trans. Biomed. Eng. , vol. 58, no. 7, pp. 1959-1966, Jul. 2011. http://www.ncbi.nlm.nih.gov/pubmed/21245000 [15] J. F. G. de Freitas, M. Niranjan, and A. H. Gee, "Hierarchical Bayesian models for regularization in sequential learning, "Neural Comput. , vol. 12, no. 4, pp. 933-953, Apr. 2000. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6789428 [16] Y. S. T. Hong, "Dynamic nonlinear state-space model with a neural network via improved sequential learning algorithm for an online real-time hydrological modeling, "J. Hydrol. , vol. 468-469, pp. 11-21, Oct. 2012. http://www.sciencedirect.com/science/article/pii/S0022169412006658 [17] Y. H. Xi, H. Peng, and X. H. Chen, "A sequential learning algorithm based on adaptive particle filtering for RBF networks, "Neural Comput. Appl. , vol. 25, no. 3-4, pp. 807-814, Sep. 2014. http://dl.acm.org/citation.cfm?id=2662643 [18] N. Y. Zeng, Z. D. Wang, Y. R. Li, M. Du, and X. H. Liu, "A hybrid EKF and switching PSO algorithm for joint state and parameter estimation of lateral flow immunoassay models, "IEEE/ACM Trans. Comput. Biol. Bioinform. , vol. 9, no. 2, pp. 321-329, Mar. -Apr. 2012. [19] N. Y. Zeng, Z. D. Wang, Y. R. Li, M. Du, and X. H. Liu, "Identification of nonlinear lateral flow immunoassay state-space models via particle filter approach, "IEEE Trans. Nanotechnol. , vol. 11, no. 2, pp. 321-327, Mar. 2012. http://ieeexplore.ieee.org/abstract/document/6081979/ [20] M. Hürzeler and H. R. Künsch, "Approximating and maximising the likelihood for a general state-space model, "in Sequential Monte Carlo Methods in Practice, A. Doucet, N. de Freitas, and N. Gordon, Eds. New York: Springer, 2001, pp. 159-175. http://www.ams.org/mathscinet-getitem?mr=1847791 [21] N. Y. Zeng, Z. D. Wang, Y. R. Li, M. Du, J. Cao, and X. H. Liu, "Time series modeling of nano-gold immunochromatographic assay via expectation maximization algorithm, "IEEE Trans. Biomed. Eng. , vol. 60, no. 12, pp. 3418-3424, Dec. 2013. http://www.ncbi.nlm.nih.gov/pubmed/23629840 [22] M. Lázaro, I. Santamaría, and C. Pantaleón, "A new EM-based training algorithm for RBF networks, "Neural Netw. , vol. 16, no. 1, pp. 69-77, Jan. 2003. http://dl.acm.org/citation.cfm?id=776140 [23] C. Constantinopoulos and A. Likas, "Semi-supervised and active learning with the probabilistic RBF classifier, "Neurocomputing, vol. 71, no. 13-15, pp. 2489-2498, Aug. 2008. http://www.sciencedirect.com/science/article/pii/S0925231208002117 -
下载:
计量
- 文章访问数: 1636
- HTML全文浏览量: 391
- PDF下载量: 2142
- 被引次数: 0
