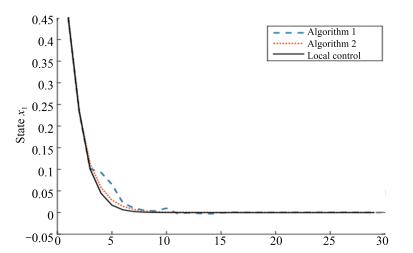
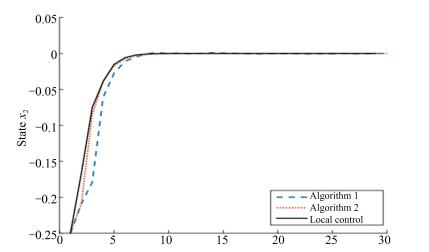
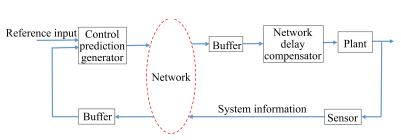
Optimization Algorithms for Predictive Control Approach to Networked Bilinear Systems
-
Abstract: This paper is concerned with the networked predictive control of discrete-time bilinear systems. To deal with the network-induced communication delay that exists in both forward channel (controller to actuator) and feedback channel (sensor to controller), a bilinear networked predictive control scheme is proposed. Then a non-convex optimization problem of solving the predictive control sequence is presented, for which two gradually-optimized algorithms are proposed based on the special structure of bilinear system dynamics model. The numerical simulation indicates that the resulting predictive control sequence can compensate for the network-induced issues actively, which proves the effectiveness of the proposed predictive control strategy.
-
Key words:
- Bilinear systems /
- networked control systems (NCSs) /
- non-convex optimization /
- predictive control
-
当前, 用于信号恢复的稀疏重构算法主要分为两大类:凸优化算法和贪婪算法.通常情况下, 利用基于$L_1$范数的凸优化算法来解稀疏恢复的欠定问题.因而信号恢复问题转化成寻求凸函数的最优解问题.常见凸函数求解算法有基追踪算法(Basis pursuit, BP[1]、最小角回归算法(Least angle regression, LARS[2]、梯度投影稀疏重构算法(Gradient projection sparse reconstruction, GPSR[3]等.凸优化方法给出了最强的稀疏恢复的保证, 在测量矩阵满足一定的条件下它能精确重建所有的稀疏信号, 同时需要测量的次数也较少[4], 然而, 其最大的缺点在于重建速度慢, 对于大尺度的重建问题实现困难.
贪婪算法主要思想是利用采样矩阵在投影序列中搜索最稀疏的矢量[5].目前贪婪算法包括正交匹配追踪(Orthogonal matching pursuit, OMP[6]、稀疏自适应匹配追踪(Sparsity adaptive matching pursuit, SAMP[7]、正则正交匹配追踪(Regularized orthogonal matching pursuit, ROMP[8]、分级正交匹配追踪(Stagewise orthogonal matching pursuit, StOMP[9]和压缩感知匹配追踪(Compressive sampling orthogonal matching pursuit, CoSaOMP[10-11].目前, 贪婪算法是重建速度最快的算法, 尽管最初提出的OMP算法在重建效率上并不是很理想, 论是在重建速度还是重建精度上都得到了很大改进.
通常, 凸优化算法能在较低采样率下实现精确的重构, 但也带来了计算上的巨大开销, 且其算法迭代次数容易受到收敛标准的干扰[12].匹配追踪算法对低维和小尺度的信号数据表现出较好的性能.然而, 如果信号受到噪声干扰, 或者处理尺度较大, 其重构的精度和健壮性得不到保障.
本文提出一种基于共轭梯度最小二乘法(Conjugate gradient least squares, CGLS)和最小二乘QR分解(Least squares QR, LSQR)联合优化的匹配追踪算法实现噪声干扰下的精确的稀疏恢复. CGLS方法是一种解决不对称线性方程和最小二乘问题的共轭梯度法[13], LSQR是基于双对角化的Golub和Kahan方法[14]. LSQR与标准的共轭梯度法类似, 但其拥有更好的数值处理特性. CGLS和LSQR这两种方法能够用于解约束条件为$\min \| Ax - b\|_2$方程式, 其中$A$是一个高维稀疏矩阵.两种算法对不同的数据拟合表现出不同的精准性.本文利用Alpha散度来度量两种方法间的离差度, 实现在稀疏恢复中两种方法交替迭代选择最优的解.实验表明本文提出的方法在噪声干扰的环境下其性能优于传统匹配追踪算法的重构性能.
1. 基本问题描述
目前匹配追踪系列算法主要思路在于对下列最小二乘问题找到一个最优解:
$ \begin{equation} {\left\| {{\pmb b} - {{A}}{\pmb x}} \right\|_2} = \mathop {\min }\limits_{y \in {{\bf R}^n}} {\left\| {{\pmb b} - {{A}}{\pmb y}} \right\|_2} \end{equation} $
(1) 对于该问题, 这里引入分裂迭代法和Krylov子空间迭代法进行求解.在Krylov子空间, 对于标准的最小二乘问题, LSQR求解方式类似于共轭梯度算法.在利用匹配追踪求解${x_k}$的过程中, 它们都能实现残量$\|r_k\| ({r_k} = b - A{x_k})$的逐步约减, 同时进一步说明了LSQR和CGLS的交替迭代能产生最佳的解序列的可能.本文任务在于如何在LSQR和CGLS之间选择最优解序列使匹配追踪的残量最小化, 从而确保解序列的最优性.
2. 共轭梯度最小二乘法
假定${{A}} \in {{\bf R}^{m \times n}}$, 考虑LS问题(1)对应的法方程为
$ \begin{equation} {{{{A}}^{\rm T}}{{A}}{\pmb x} = {{{A}}^{\rm T}}{\pmb b}} \end{equation} $
(2) 这里${A^{\rm T}}A$是$n$阶实对称矩阵.则求解线性方程组的问题可以转化为求二次函数(3)的极小点问题.
$ \begin{equation} {f({\pmb x}) = \frac{1}{2}{{\pmb x}^{\rm T}}{{{A}}^{\rm T}}{{A}}{\pmb x} -{({{{A}}^{\rm T}}{\pmb b})^{\rm T}}{\pmb x}} \end{equation} $
(3) 事实上, 函数$f({\pmb x})$的梯度$g({\pmb x})$为
$ \begin{align} g({\pmb x}) =\,&\nabla f({\pmb x}) = \left[\frac{{\partial f}}{{\partial {x_1}}}, \cdots, \frac{{\partial f}}{{\partial {x_n}}}\right]^{\rm T}=\nonumber\\& {A^{\rm T}}A{\pmb x} - {A^{\rm T}}{\pmb b} \end{align} $
(4) 进一步, 对于任意的非零向量${\pmb p} \in {{\bf R}^n}$和实数$t$, 有
$ \begin{equation} {f({\pmb x} + t{\pmb p}) -f({\pmb x}) \approx tg^{\rm T}{({\pmb x})}{\pmb p}+ \frac{1}{2}{t^2}{{\pmb p}^{\rm T}}{A^{\rm T}}A{\pmb p}} \end{equation} $
(5) 若${\pmb u}$是函数(2)的解, 则有$g({\pmb u})=0$.因此对任意的非零向量${\pmb p}\in{{\bf R}^n}$, 则有如下子问题:
$ f({\pmb u} + t{\pmb p}) - f({\pmb u})\left\{ \!\!\begin{array}{ll} > 0, &t \ne 0 \\ = 0, &t = 0 \end{array} \right. $
故${\pmb u}$是函数$f({\pmb x})$的极小点.反之, 因${A^{\rm T}}A$正定, 所以在${{\bf R}^n}$中二次函数$f({\pmb x})$有唯一的极小点, 若${\pmb u}$是$f({\pmb x})$的极小点, 则
$ \begin{equation} {f({\pmb u} + t{\pmb p}) - f({\pmb u}) = tg^{\rm T}{({\pmb u})}{\pmb p} + \frac{1}{2}{t^2}{{\pmb p}^{\rm T}}{{{A}}^{\rm T}}{{A}}{\pmb p}} \end{equation} $
(6) 于是有
$ \begin{equation} {\frac{{{\rm d}f({\pmb u }+ t{\pmb p})}}{{{\rm d}t}}{|_{t = 0}} = g^{\rm T}{({\pmb u})}{\pmb p} = 0} \end{equation} $
(7) 考虑到${\pmb p}$的随机性, 必须有$g({\pmb u})=0$, 从而${\pmb u}$是方程组(2)的解.若向量序列${{\pmb p}^{(0)}}, {{\pmb p}^{(1)}}, \cdots, {{\pmb p}^{(k - 1)}} \in {{\bf R}^n}$满足:
$ \begin{equation} {{{\pmb p}^{(i){\rm T}}}{A^{\rm T}}A{{\pmb p}^{(j)}} = 0, \quad i \ne j} \end{equation} $
(8) 且${{\pmb p}^{(k)}} \ne 0, k = 0, 1, 2, \cdots, n - 1$, 则称向量序列$\{ {{\pmb p}^{(k)}}\} $为${{\bf R}^n}$中关于${A^{\rm T}}A$的一个共轭向量序列.假定${{\pmb x}^{(0)}} \in {{\bf R}^n}$是任意给定一个初始向量, 而$k = 0, 1, 2, \cdots$, 则以${{\pmb x}^{(k)}}$作为起点沿方向${{\pmb p}^{(k)}}$求函数$f({\pmb x})$在直线${\pmb x} = {{\pmb x}^{(k)}} + t{{\pmb p}^{(k)}}$上的极小点, 则可以得到:
$ \begin{equation} {{{\pmb x}^{(k + 1)}} = {{\pmb x}^{(k)}} + {\alpha _k}{{\pmb p}_k}} \end{equation} $
(9) $ \begin{equation} {{{\pmb s}^{(k)}} = {{{A}}^{\rm T}}({\pmb b} - A{{\pmb x}^{(k)}}), ~{\alpha _k} = \frac{{{{\pmb s}^{(k){\rm T}}}{{\pmb p}^{(k)}}}}{{{{\pmb p}^{(k){\rm T}}}{{{A}}^{\rm T}}{{A}}{{\pmb p}^{(k)}}}}} \end{equation} $
(10) 这里${{\pmb p}^{(k)}}$表示了搜索方向, 式(9)称为共轭方向法.特别地, 如果取${{\pmb p}^{(0)}} = {{\pmb s}^{(0)}}$, 有:
$\begin{align} &{{\pmb p}^{(k + 1)}} = {{\pmb s}^{(k + 1)}} + {\beta _k}{{\pmb p}^{(k)}}\nonumber\\& {\beta _k} = - \frac{{{{\pmb s}^{(k + 1){\rm T}}}{A^{\rm T}}A{{\pmb p}^{(k)}}}}{{{{\pmb p}^{(k){\rm T}}}{A^{\rm T}}A{{\pmb p}^k}}} \end{align} $
(11) 则为共轭梯度法.由式$(9)\, \sim\, (11)$可知, 若存在$k \ge 0$, 使${{\pmb s}^{(k)}} = 0$, 则${{\pmb x}^{(k)}}$为LS问题的解, 且有${\alpha _k} = {\beta _k} = 0, {{\pmb s}^{(k + 1)}} = {{\pmb p}^{(k + 1)}} = 0$.为了更清晰地展示CGLS算法的执行步骤, 下面给出了CGLS算法流程:
算法1. 共轭梯度最小二乘算法(CGLS)
输入: ${{A}} \in {{\bf R}^{m \times n}}, {\pmb b} \in {{\bf R}^m}$, 迭代终止阈值$tol > 0$
输出: 解序列$x$
1) 初始化: ${{\pmb x}^{(0)}} \in {{\bf R}^n}$
2) ${{\pmb r}^{(0)}} = {\pmb b} - {{A}}{{\pmb x}^{(0)}}$, $Q{{\pmb p}^{(0)}} = {{\pmb s}^{(0)}} = {{{A}}^{\rm T}}{{\pmb r}^{(0)}}, {\gamma _0} = \left\| {{{\pmb s}^{(0)}}} \right\|_2^2$
3) for $ i=0, 1, 2, 3, \cdots, $当${\gamma _k} > tol$时, 重复如下步骤
4) ${{\pmb q}^{(k)}} = {{A}}{{\pmb p}^{(k)}}, {\alpha _k} = {\gamma _k}/\left\| {{{\pmb q}^{(k)}}} \right\|_2^2$
5) ${{\pmb x}^{(k + 1)}} = {{\pmb x}^{(k)}} + {\alpha _k}{{\pmb p}^{(k)}}$, ${{\pmb r}^{(k + 1)}} = {{\pmb r}^{(k)}} - {\alpha _k}{{\pmb q}^{(k)}}$
6) ${{\pmb s}^{(k + 1)}} = {A^{\rm T}}{{\pmb r}^{(k + 1)}}$; ${\gamma _{k + 1}} = \left\| {{{\pmb s}^{(k + 1)}}} \right\|_2^2$
7) ${\beta _k} = {\gamma _{k + 1}}/{\gamma _k}$; ${{\pmb p}^{(k + 1)}} = {{\pmb s}^{(k + 1)}} + {\beta _k}{{\pmb p}^{(k)}}$
结束
CGLS方法是通过迭代求出$x$序列$({x_1}, {x_2}, \cdots, {x_k})$.当CGLS迭代次数增加, 或者矩阵$A$是病态矩阵时, 由CGLS产生的序列的方差偏大.由于LSQR与CGLS产生的序列相近, 我们引入LSQR方法和CGLS方法进行并行运算, 每步迭代产生$\pmb x(k)~(k = 1, 2, \cdots)$, 并选择最优$\pmb x(k)$作为下步迭代的输入, 如此迭代执行, 直至收敛.这里我们给出LSQR迭代算法, 然后在后面部分讨论解序列的最优选择方式.
3. 最小二乘QR算法
最小二乘QR (Least squares QR, LSQR)是在Lanczos双对角化(Lanczos bidiagonalization, LBD)的基础上得到的, 其和共轭梯度法一样可以用于求解方程$({A^{\rm T}}A + {\lambda ^2}I){\pmb x} = {A^{\rm T}}{\pmb b}$.通过对残量${\pmb r_k} = {\pmb b} - {{A}}{{\pmb x}_k}$的逐步约减去逼近最优解序列$\{ {x_k}\}$.设${{A}} \in {{{{\bf R}}}^{m \times n}}, m \ge n$, 则分别存在$m$阶和$n$阶正交矩阵${\pmb U} = ({{u}_1}, \cdots, {{u}_m}), V = ({{v}_1}, \cdots, {{u}_n}), {U_1} = ({{u}_1}, \cdots, {{u}_n})$, 和双对角矩阵
$ \begin{eqnarray*} {{B}} = {{{B}}_n} = \left[{\begin{array}{*{20}{c}} {{\alpha _1}}&{}&{}&{}\\ {{\beta _2}}&{{\alpha _2}}&{}&{}\\ {}&{{\beta _2}}&{\ddots}&{}\\ {}&{}&{\ddots}&{{\alpha _n}}\\ {}&{}&{}&{{\beta _{n + 1}}} \end{array}} \right]\in {{\bf{{\bf R}}}^{(n + 1) \times n}}\\ \end{eqnarray*} $
且满足${{A}} = {\pmb{U}}\left( {\frac{{{B}}}{{{{{U}}_1}}}} \right){V^{\rm T}}$或等价于${{AV}} = {{{U}}_1}{{B}}, {{{A}}^T}{{{U}}_1} = {{V}}{{{B}}^{\rm T}}$.这里${B_n}$不是方阵, 进一步令${\beta _1}{{\pmb v}_0} = 0, {\alpha _{n + 1}}{{\pmb v}_{n + 1}} = 0$, 可以得到递推关系:
$ \begin{equation} {{{A}}^{\rm T}}{{\pmb u}_j} = {\beta _j}{{\pmb v}_{j - 1}} + {\alpha _j}{{\pmb v}_j} \end{equation} $
(12) $ \begin{equation} {A{{\pmb v}_j} = {\alpha _j}{{\pmb u}_j} + {\beta _{j + 1}}{{\pmb u}_{j + 1}}, \quad j = 1, 2, \cdots, n} \end{equation} $
(13) 给定初始向量${{\pmb u}_1} \in {{\bf R}^m}, {\left\| {{{u}_1}} \right\|_2} = 1$, 对于$j = 1, 2, \cdots$, 有:
$ \begin{equation} {r_j} = {{{A}}^{\rm T}}{{\pmb u}_j} - {\beta _j}{{\pmb v}_{j - 1}}, {\alpha _j} = {\left\| {{r_j}} \right\|_2}, {{\pmb v}_j} = \frac{r_j}{\alpha _j} \end{equation} $
(14a) $ \begin{equation} {{\pmb p}_j} = {{A}}{{\pmb v}_j} - {\alpha _j}{{\pmb u}_j}, {\beta _{j + 1}} = {\left\| {{{\pmb p}_j}} \right\|_2}, {{\pmb u}_{j + 1}} = \frac{{\pmb p}_j}{\beta _{j + 1}} \end{equation} $
(14b) 求得${B_n}$的元素${\alpha _i}, {\beta _i}$和向量${{\pmb v}_i}, {{\pmb u}_i}$.理论上, 在LBD过程式(14)中, 取${{\pmb u}_1} = {\pmb b}/{\left\| {\pmb b} \right\|_2}$为初始向量, 对$A{A^{\rm T}}$和${A^{\rm T}}A$应用Lanczos过程产生的向量相同.而在浮点运算时, Lanczos向量将失去正交性, 上面的许多关系式对于足够的精度要求将不再成立.尽管如此, 截断的双对角矩阵${B_k} \in {{\bf R}^{(k + 1) \times k}}$的最大和最小奇异值能很好地逼近$A$的相应奇异值, 即使$k \ll n$.现在考虑计算线性最小二乘问题(1)的LSQR算法.取向量${{\pmb u}_1} = \pmb b/{\left\| \pmb b \right\|_2}$, 采用式(14)经$k$步迭代后, 得到矩阵${V_k}$, ${U_{k + 1}}$和${B_k}$.
$ \begin{equation} {{{V}}_k} = ({{\pmb v}_1}, \cdots, {{\pmb v}_k}), \quad {{{U}}_{k + 1}} = ({{\pmb u}_1}, \cdots, {{\pmb u}_{k + 1}}) \end{equation} $
(15) 其中, ${B_k}$是${B_n}$的左上角的$(k + 1) \times k$的矩阵, 且式(14)可写成
$ {\beta _1}{{{U}}_{k + 1}} = {\pmb b}, \ \ \ \ \ \ {{A}}{{{V}}_k} = {{{U}}_{k + 1}}{{{B}}_k}\\ {{A}}^{\rm T}{{{U}}_{k + 1}} = {{{V}}_k}{{B}}_k^{\rm T} + {\alpha _{k + 1}}{{\pmb v}_{k + 1}}\pmb e_{k + 1}^{\rm T} $
(16) 对于式(1)的近似解${{\pmb x}^{(k)}}$, 则可以表示为${{\pmb x}^{(k)}} = {V_k}{y^{(k)}}$, 且有:
$ \begin{equation} {{\pmb b} - {{A}}{{\pmb x}^{(k)}} = {{{U}}_{k + 1}}{{\pmb t}_{k + 1}}, {{\pmb t}_{k + 1}} = {\beta _1}{{\pmb e}_1} - {{{B}}_k}{{\pmb y}^{(k)}}} \end{equation} $
(17) 最后, 最小二乘问题转化为如下形式:
$ \begin{equation} {\mathop {\min }\limits_{{{\pmb x}^{(k)}} \in {\kappa _k}} {\left\| {{{A}}{{\pmb x}^{(k)}} - {\pmb b}} \right\|_2} = \mathop {\min }\limits_{{{\pmb y}^{(k)}}} {\left\| {{{{B}}_k}{{\pmb y}^{(k)}} - {\beta _1}{{\pmb e}_1}} \right\|_2}} \end{equation} $
(18) 这个方法从数学理论上来看, 产生和CGLS相同的近似序列.从而LSQR的收敛性质也和CGLS相同.这里我们给出LSQR算法.由于$B_k$是长方形的下双对角矩阵, 可用一系列的Givens矩阵计算它的QR分解.
$ \begin{equation} {{{Q}}_k}{{{B}}_k} = \left[{\begin{array}{*{20}{c}} {{{{R}}_k}}\\ 0 \end{array}} \right], \begin{array}{*{20}{c}} {}&{} \end{array}{{{Q}}_k}({\beta _1}{{\pmb e}_1}) = \left[{\begin{array}{*{20}{c}} {{f_k}}\\ {{{\bar \varphi }_{k + 1}}} \end{array}} \right] \end{equation} $
(19) 这里${R_k}$是上三角矩阵, ${{{Q}}_k} = {{{G}}_{k, k + 1{G_{k - 1, k}}}}\cdots{{{G}}_{1, 2}}$.通过计算
$ \begin{equation} {{{{R}}_k}{{\pmb y}^{(k)}} = {f_k}, \begin{array}{*{20}{c}} {}&{} \end{array}{{\pmb t}_{k + 1}} = {{Q}}_k^{\rm T}\left[{\begin{array}{*{20}{c}} 0\\ {{{\bar \varphi }_{k + 1}}} \end{array}} \right]} \end{equation} $
(20) 可以获得向量${\pmb y^{(k)}}$和对应的残量${\pmb t_{k + 1}}$.上述步骤不需要每一步从最开始计算.假定这里已经计算了${B_{k.1}}$的分解, 在下一步中加上第$k$列, 计算平面的旋转变换${{{Q}}_k} = {{{G}}_{k, k + 1}}{{{Q}}_k}$使得
$ {{{G}}_{k, k + 1}}{{{G}}_{k - 1, k}}\left[ {\begin{array}{*{20}{c}} 0\\ {{{\pmb \alpha} _k}}\\ {{{\pmb \beta }_{k + 1}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{{\pmb \theta }_k}}\\ {{{\pmb \rho} _k}}\\ 0 \end{array}} \right]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{{{G}}_{k, k + 1}}\left[{\begin{array}{*{20}{c}} {{{\bar {\pmb \phi} }_k}}\\ 0 \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{{\pmb \phi} _k}}\\ {{{\bar {\pmb \phi} }_{k + 1}}} \end{array}} \right]} $
(21) 理论上, LSQR和CGLS产生相同的近似序列${{x}^{(k)}}$, 然而, Paige和Sanuders证明[15], 当要执行很多迭代, 或$A$是病态矩阵时, LSQR在数值上更可靠.
根据LSQR的数值计算方法, 我们给出了LSQR算法执行的步骤:
算法2. 最小二乘的QR算法(LSQR)
输入: ${{A}} \in {{\bf R}^{m \times n}}, {\pmb b} \in {{\bf R}^m}$迭代终止阈值$tol > 0$
输出: 解序列$ \pmb x $
1) 初始化: ${{\pmb x}^{(0)}} \in {{\bf R}^n}$
2) ${{\pmb x}^{(0)}} = 0;{\beta _1}{{\pmb u}_1} = {\pmb b};{\alpha _1}{{\pmb v}_1} = {{{A}}^{\rm T}}{{\pmb u}_1}$, ${{\pmb w}_1} = {{\pmb v}_1}$; ${\bar {\pmb \varphi} _1} = {\beta _1}$; ${\bar {\pmb \rho} _1} = {{\pmb \alpha} _1};$
3) for $i=0, 1, 2, 3, \cdots, $当${w_{i + 1}} > tol$时, 重复如下步骤
4) ${\beta _{i + 1}}{{\pmb u}_{i + 1}} = {{A}}{{\pmb v}_i} - {\alpha _i}{{\pmb u}_i}$; ${\alpha _{i + 1}}{{\pmb v}_{i + 1}} = {{{A}}^{\rm T}}{{\pmb u}_{i + 1}} - {\beta _{i + 1}}{{\pmb v}_i}$
5) $({c_i}, {s_i}, {\rho _i}) = {\rm givrot}({\bar \rho _i}, {\beta _{i + 1}})$
6) ${\theta _i} = {s_i}{\alpha _{i + 1}};{\bar \rho _{i + 1}} = {c_i}{\alpha _{i + 1}}$; ${\varphi _i} = {c_i}{\bar \varphi _i};{\bar \varphi _{i + 1}} = - {s_i}{\bar \varphi _i}$
7) ${{\pmb x}^{(i)}} = {{\pmb x}^{(i - 1)}} + ({\varphi _i}/{\rho _i}){{\pmb w}_i}$; ${{\pmb w}_{i + 1}} = {{\pmb v}_{i + 1}} - ({\theta _i}/{\rho _i}){{\pmb w}_i}$
结束
这里givrot为计算givens旋转的算法, 旋转的纯量${\alpha _i} \ge 0$和${\beta _i} \ge 0$使得相应的向量单位化.
4. 基于CGLS与LSQR的组合优化匹配追踪算法
通常, 根据CGLS算法和LSQR算法对最小二乘问题进行求解, 可以得到两组解序列.但这两组解序列并不是最优解, 特别在压缩感知过程中, 受到噪声干扰时, 匹配追踪的算法通过求解最小二乘问题恢复得到的信号精度较低(比如在测量值包含了高斯白噪声的情况下, 实验表明其恢复精度下降比较严重).因此, 针对噪声环境下的稀疏恢复问题可以表示为
$ \begin{equation} {{\pmb b} = A{\pmb x} + {\pmb z}} \end{equation} $
(22) 其中, ${\pmb z}$表示噪声干扰项, ${\left\| {\pmb z} \right\|_2} < \varepsilon $.对于式(22)仍然可以通过$L_1$范数的最小化约束来求解
$ \begin{equation} {\hat {\pmb x }= \arg \min {\left\| {\pmb x} \right\|_1}, {\left\| {A{\pmb x} - {\pmb b}} \right\|_2} \le \varepsilon } \end{equation} $
(23) 为了求解式(23), 我们提出一种方法用于提高噪声干扰下的稀疏恢复的精度.该方法通过从算法1和算法2产生的解序列中迭代选择出最优的序列去逼近真实解, 从而确保精确恢复.为了判断和选择每步迭代中产生的两种解序列哪个更优, 这里我们采用了Alpha散度来计算两个解序列间的离差程度, 并设定离差度阈值, 通过对两种序列的Alpha散度的计算与离差阈值的比较, 选择较优的解序列作为两种算法下一迭代的输入, 循环执行, 直到收敛.
Alpha散度, 也称为Renyi散度, 是信息几何学中所提出的概念, 它主要用于对两个数据集之间的差异度进行度量[16].对于两个数据集$\pmb p$和$\pmb q$, 其Alpha散度对象函数表示为
$ \begin{equation} {{D_\alpha }[{\pmb p}||{\pmb q}] = \frac{1}{{\alpha (1 - \alpha )}}\int {\alpha {\pmb p} + (1 - \alpha ){\pmb q} - {{\pmb p}^\alpha }} {{\pmb q}^{1 - \alpha }}{\rm d}\mu} \end{equation} $
(24) 其中, $\alpha \in ( - \infty, \infty )$.对于Alpha散度而言有如下特性:
1) Alpha散度的函数(${D_\alpha }[p||q]$)相对于$p$与$q$而言是凸函数.
2) 当$p = q$, ${D_\alpha }[{\pmb p}||{\pmb q}]{\rm{ = }}0$
3) 在$p \ne q$时, ${D_\alpha }[{\pmb p}||{\pmb q}] \ge 0$
Alpha散度函数表达式(24), 通常也表示为
$ \begin{align} {D_\beta }[{\pmb p}||{\pmb q}] = \, &\frac{4}{{(1 - \beta )}}\int {\frac{{1 - \beta }}{2}} p + \nonumber\\&\frac{{1 + \beta }}{2}q - {{ p}^{\frac{{1 - \beta }}{2}}}{q^{\frac{{1 + \beta }}{2}}}{\rm d}\mu \end{align} $
(25) 其中, $\alpha = {{(1 - \beta )}}/{2}$, 因此$1 - \alpha = {{(1 + \beta) }}/{2}$.当Alpha散度用于离散数据集的度量时, 数据集$p$和$q$的Alpha散度表达式为
$ \begin{align} {D_\alpha }[{\pmb p}||{\pmb q}] =\,&\frac{1}{{\alpha (1 - \alpha )}}\sum\limits_{i = 1}^m \sum\limits_{j = 1}^n \alpha {p_{ij}} + \nonumber\\&(1 - \alpha ){q_{ij}} - Y_{ij}^\alpha q_{ij}^{1 - \alpha } \end{align} $
(26) 依据式(25), 式(26)通常被表示为
$ \begin{equation} {{D^\beta }({\pmb q}{\rm{||}}{\pmb p}) = \sum\limits_{ik} {{p_{ik}}} \dfrac{{{{\left(\dfrac{p_{ik}}{q_{ik}}\right)}^{\beta - 1}} - 1}}{{\beta (\beta - 1)}} + \frac{{{q_{ik}} - {p_{ik}}}}{\beta }} \end{equation} $
(27) 其中, $\beta = (1 + \alpha )/2$由Alpha散度作为两种算法产生序列的离差度量标准, 可以避免采用单一算法进行恢复或者采用传统欧氏距离作为数据集差异标准进行恢复而带来的收敛到局部最优, 从而造成在噪声干扰下的恢复精度不高的缺点.因此我们可以通过Alpha散度在每步迭代中来优化选择解序列, 从而得出更精确解.根据Alpha散度理论, 我们选择恰当的$\beta$ $(\beta = 0.5)$值建立散度方程[17].同时为了确保收敛方向和加快收敛速度, 引入了权重参数$1/{{w}_i} = {\left| {x_i^{(n)}} \right|^2}$.权重${{\pmb w}_{(n)}}$是通过上一步的值${\pmb w_{(n - 1)}}$迭代计算出来, 权重参数可以逐步修正收敛方向.为了计算权重参数$\pmb w$, 这里进一步定义产生函数, 对于$\varepsilon > 0$和权重${\pmb w} \in {\bf R}$, ${w_j} > 0, j = 1, \cdots, N$, 有:
$ \begin{align} {\cal F}z, {\pmb w}, \varepsilon =\,&\frac{1}{2}\left[ {\sum\limits_{j = 1}^N {z_j^2} {w_{_j}} + \sum\limits_{j = 1}^N {({\varepsilon ^2}{w_j} + w_j^{-1})} } \right], \nonumber\\&\qquad\qquad{z \in {{\bf R}^N}} \end{align} $
(28) 由于${\cal F}$是凸的, 因此对于给定$\pmb w$和$\varepsilon $, 可以求$z$使函数${\cal F}$最小化0.这里通过迭代法来确定函数${\cal F}$的最小值和每次迭代的权重.为了方便分析这个过程, 假定$r(z)$是对$z$的绝对值按降序排列的集合, $z \in {{\bf R}^N}$, 因此$r{(z)_i}$是集合$\{ |{Z_j}|, j = 1, \cdots, N\} $中第$i$个最大元素.因此我们选取初始值${w^0} = (1, \cdots, 1), {\varepsilon _0} = 1$, ${x_{n + 1}}$的迭代计算式为
$ \begin{equation} {{{x}^{n + 1}} = \arg \mathop {\min }\limits_{z \in {\bf R}} {\cal F}(z, {w^n}, {\varepsilon _n}) = \arg \mathop {\min }\limits_{z \in {\bf R}} {\left\| z \right\|_{l2({w^n})}}} \end{equation} $
(29) 其中, ${\varepsilon _{n + 1}} = \min ({\varepsilon _n}, \frac{{r{{({{x}_{n + 1}})}_{K + 1}}}}{N})$故权重系数$w$的迭代表示为
$\begin{equation} {{w_{n + 1}} = \arg \mathop {\min}\limits_{w > 0} {\cal F}({{ x}_{n + 1}}, w, {\varepsilon _{n + 1}})} \end{equation} $
(30) 计算权重系数的关键在于需要每次迭代求解${x_{n + 1}}$, 根据最小二乘的计算方法,
$ \begin{equation} {{{\pmb x}^{n + 1}} = {D_n}{\Phi ^{\rm T}}{(\Phi {D_n}{\Phi ^t})^{ - 1}}{\pmb y}} \end{equation} $
(31) 其中, ${D_n}$是$N \times N$的对角矩阵, 它的第$j$个对角元素是$w_j^n$, 通过求解${x_{n + 1}}$, 则权重${w_{n + 1}}$可以下式求出
$\begin{equation} {w_j^{n + 1} = {({(x_j^{n + 1})^2} + \varepsilon _{n + 1}^2)^{ - \frac{1}{2}}}, \quad j = 1, \cdots, N} \end{equation} $
(32) 根据上面的分析, 我们给出基于CGLS和LSQR的联合优化的匹配追踪算法(Combinatorial Optimization MP Based CGLS and LSQR, COCLMP), 该算法本质上也是寻求式(1)的最优解.算法流程如下:
算法3. 基于CGLS与LSQR的组合优化匹配追踪算法
输入: 感知矩阵$\Phi $, 测量向量$\pmb b$, 权重阈值$\varepsilon$, 收敛阈值$\delta$
输出: $\pmb x$的稀疏逼近$\hat {\pmb x}$ ($\pmb x$的解), 重建误差$\pmb r$
1) 初始化冗余向量${\pmb r}_0 = {\pmb y}$, 索引集合${\Lambda _t} = \varphi $, 迭代计数$t=1$
2) 循环开始
找到索引${\lambda _t}$使得${\lambda _t} = \arg \mathop {\max }\limits_{j \in (M - {\Lambda _t})} | \langle {{\pmb r}_{t - 1}}, {\Phi _j} \rangle |$, $M={1, 2, \cdots, M}$表示集合$M$中去掉${\Lambda _t}$中的元素
3) 令${\Lambda _t} = {\Lambda _{t - 1}} \cup \{ {\lambda _t}\} $
4) 计算新的近似$\hat{\pmb x}_j = \Phi _{{\Lambda _t}}^ \bot{\pmb y}$, 其中${\Phi ^ \bot }$表示$\Phi$的伪逆
$ {\Phi ^ \bot } = {({\Phi ^{\rm T}}\Phi )^{ - 1}}{\Phi ^{\rm T}} $
5) ${\pmb y}^{(j)}$ $\leftarrow$ LSQR $(\Phi_{\Lambda_t}, b, {\hat x_j} )$ ${\hat x_j}$作为LSQR算法的初始向量
${\pmb z}^{(j)}$ $\leftarrow$ CGLS $(\Phi_{\Lambda_t}, b, {\hat x_j} )$ ${\hat x_j}$作为CGLS算法的初始向量
$ w_j^{n + 1} = {({(x_j^{n + 1})^2} + \varepsilon _{n + 1}^2)^{ - 1/2}}, j = 1, \cdots, N $
6) 计算两个序列的Alpha散度
${D^\beta }({y^{(j)}}{\rm{||}}{{{\pmb z}}^{(j)}}) = \sum\limits_{ik} {{p_{ik}}} \frac{{{{(z_{ik}^{(j)}/y_{ik}^{(j)})}^{\beta - 1}} - 1}}{{\beta (\beta - 1)}} + \frac{{y_{ik}^{(j)} - z_{ik}^{(j)}}}{\beta} $
如果${D^\beta }({{\pmb x}_1}{\rm{||}}{{\pmb x}_2}) < tol$
$ \hat{\pmb x}_j \leftarrow {\pmb w}{{\pmb y}_1} + (1 - {\pmb w}){{\pmb z}_2} $
否则
$ {\hat {\pmb x}_j} \leftarrow (1 - {\pmb w}){{\pmb y}_1} + {\pmb w}{{\pmb z}_2} $
7) 当${\left\| {{{\hat{\pmb x}}_j} - {{\hat{\pmb x}}_{j - 1}}} \right\|_2} \le \delta $或者达到迭代次数, 转到步骤8;否则, 转到步骤5, ${\hat{\pmb x}_j}$作为LSQR和CGLS的输入.
8) ${\pmb x} = {\hat {\pmb x}_j}$
9) 更新冗余向量
10)如果满足${\left\| {{{\pmb r}_t} - {{\pmb r}_{t - 1}}} \right\|_2} < \varepsilon $ or $ N = {\Lambda _t}$, 则输出${\pmb x}$, ${\pmb r}={\pmb r}_i, $
算法结束; 否则, $t=t+1 $转步骤2.
COCLMP算法是用上一步的解序列作为下一步LSQR和CGLS算法的输入产生新的解序列, 然后通过Alpha散度选择较优解序列, 作为下一次LSQR和CGLS算法的输入, 不断迭代, 直到满足收敛条件. COCLMP算法最大的特点在于通过Alpha散度度量两个解序列的差异进而使得解序列逐步逼近最优解.目前大多数匹配追踪算法进行稀疏恢复的过程中, 都采用了把解欠定方程问题, 转变为一个解最小二乘问题的思路, 而COCLMP算法通过迭代优化求解的方法得到序列的方式, 相对于OMP、StOMP、CoSaOMP、ROMP等算法来说可以提高恢复精度.
这里分析一下COCLMP算法的复杂度, 算法开始时, 为了求解索引${\lambda _t}$, 需要感知矩阵$\Phi $与误差$r$内积运算O$(mNM)$次, $m$是算法需要的迭代次数, LSQR与CGLS的计算复杂度分别为O$(M{n^2})$和O$(m\sqrt{n})$, COCLMP算法的迭代包含了LSQR与CGLS的计算过程, 因此整个COCLMP算法时间复杂度为O$({m^2}nM)$.从以上分析上可以看出, COCLMP算法时间复杂度略高于单独每个的算法.
进一步, 可以讨论算法的收敛性.这里考虑COCLMP算法恢复任意一个$K$稀疏信号需要的迭代次数的上界.给定一个任意$K$稀疏信号${\pmb x}$, 按照其降序的形式排列它的元素.假设有:
$ \left| {{x_1}} \right| \ge \left| {{x_2}} \right| \ge \cdots \ge \left| {{x_K}} \right| > 0 $
并且有${x_j} = 0, \forall j > K$.进一步定义
$ \begin{equation} {{\rho _{\min }}{\rm{ = }}\frac{{\left| {{x_k}} \right|}}{{{{\left\| {{\pmb x}} \right\|}_2}}}{\rm{ = }}\frac{{\mathop {\min }\limits_{1 \le i \le K} {x_i}}}{{\sqrt {\sum\limits_{i = 1}^K {x_i^2} } }}} \end{equation} $
(33) 令${n_{it}}$代表算法恢复信号$\pmb x$的迭代次数, 那么可以根据${c_k}$ (信号的稀疏度)和${\rho _{\min }}$确定${n_{it}}$的上界.令$\tilde T$为$T$在$\frac{{{\rm{ - }}\log {\rho _{\min }}}}{{{\rm{ - }}\log {c_K}}}{\rm{ + }}1$次迭代后的估计.假设$T \not\subset \tilde T$, 则有:
$ \begin{equation} {{\left\| {{{\pmb{x}}_{T - \tilde T}}} \right\|_2} = \sqrt {\sum\limits_{i \in T - \tilde T} {x_i^2} } \ge \mathop {\min }\limits_{i \in T} \left| {{x_i}} \right| = {\rho _{\min }}{\left\| {{\pmb x}} \right\|_2}} \end{equation} $
(34) 考虑到算法以Alpha散度作为每步迭代过程逐步收敛, 因此有:
$ \begin{align} {D^\beta }({{{\pmb x}}_{T - \tilde T}}{{||x}}) \le\, & {({c_k})^{{n_{it}}}}{\rho _{\min }}{D^\beta }({{{\hat {\pmb x}}}_{T - \tilde T}}{{||{\pmb x}}}) \le \nonumber\\ &{\rho _{\min }}{D^\beta }({{{\hat {\pmb x}}}_{T - \tilde T}}{{||{\pmb x}}}) \end{align} $
(35) 其中, 后面的不等式根据${c_k} < 1$的假设, 与${c_k}$的定义矛盾, 所以有${n_{it}} < \frac{{ - \log {\rho _{\min }}}}{{ - \log {c_K}}} + 1$, 且存在${n_{it}} < \frac{{1.5K}}{{ - \log {c_K}}}$, 所以算法的上界为
$ \begin{equation} {{n_{it}} \le \min \left( {\frac{{ - \lg {\rho _{\min }}}}{{ - \lg {c_K}}} + 1, \frac{{1.5K}}{{ - \lg {c_K}}}} \right)} \end{equation} $
(36) 5. 实验及分析
本节通过实验进一步分析我们提出的基于LSQR和CGLS联合优化方法与其他重构算法的重构能力, 分析其在噪声干扰下进行稀疏重构的性能.实验中噪声干扰的强度采用SNR (Signal to noise ratio, SNR)表示, 取值为10, 20, 30, $\cdots, $ 100.实验对OMP、StOMP、CoSaOMP、ROMP和COCLMP分别进行.这前几种算法都属于匹配追踪算法系列, 它们共同的特点把解欠定方程问题转化为一个最小二乘问题.通常情况匹配追踪系列算法在对最小二乘问题求解时, 大都采用求伪逆的方式来寻找近似解, 但是在压缩感知过程中, 噪声的干扰使得这样的方式重构的信号精度较差, 而COCLMP算法可以较好地解决这类问题, 能实现较好的重构精度.
5.1 噪声干扰的稀疏信号重构
当压缩采样过程中, 信号受到噪声干扰, 其重构效果也会受到影响.在这个部分, 我们进行噪声干扰下的压缩采样和重构的实验.这里采用高斯白噪声叠加到原始信号上的方式形成混合信号, 用SNR表示原信号与噪声的强度的关系, SNR值越小相对于原信号而言噪声能量越大.这里SNR的取值为10, 20, 30, $\cdots, $ 100.实验中采用长度$N = 1\, 024, $稀疏度$s = 60$的信号, 利用随机矩阵作为采样矩阵.实验分析表明了采样次数为600是较好的采样次数[12], 因此我们构建的随机矩阵仅需要600行来生成采样矩阵.
为了量化实验结果, 这里采用原信号${x_{ture}}$与重构信号${x_{rec}}$的信躁比(SNR)来表示恢复结果, SNR定义如下:
$ \begin{equation} {{\rm SNR}({x_{\rm true}}, {x_{rec}}) = 20\lg\frac{{{{\left\| {{x_{\rm true}}} \right\|}_2}}}{{{{\left\| {{x_{\rm true}} - {x_{rec}}} \right\|}_2}}}} \end{equation} $
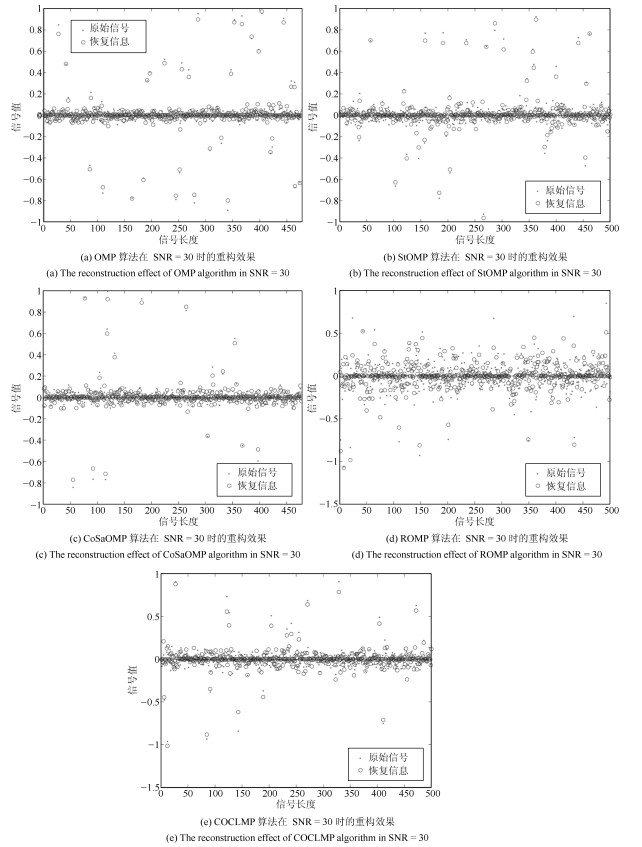
(37) 我们对比了OMP、StOMP、CoSaOMP、ROMP、COCLMP这5种算法在噪声影响下的恢复效果. 图 1展示了在压缩采样的次数为600的情况下, 带有噪声的重构效果.其中采样时原信号与噪声的SNR值为30, 经过不同算法恢复后再次计算SNR值, 经观测可得到OMP算法的SNR值为13.2507, StOMP算法的SNR值为14.0217, CoSaOMP算法的SNR值为12.0766, ROMP的SNR值为9.1521, COCLMP的SNR为16.841.从图 1中也可以看出ROMP算法重构效果较其他算法差(实心圆代表的原始信号, 与空心圆代表的恢复信号的重合程度较其他算法低).
图 1 OMP、StOMP、CoSaOMP、ROMP和COCLMP在噪声干扰下对稀疏信号的重构效果Fig. 1 Reconstruction effect of sparse signals include noise for OMP, StOMP, CoSaOMP, ROMP, COCLMP为了进一步分析4种算法在噪声下的重构性能, 考虑高斯白噪声下, SNR = 10, 20, 30, $\cdots, $ 100, 对每种强度的噪声进行100次重复实验, 观测平均SNR (其计算方法如式(37))的变化情况.
如图 2所示, OMP、StOMP、CoSaOMP、ROMP、COCLMP这5种算法在噪声影响下对信号的重构性能.测量阶段较低的SNR意味着噪声能量较强, 可以看出这5种算法在高能噪声下的恢复能力并不强, 其重构性能较差.这说明对于干扰比较严重的情况下, 压缩感知要想完整地重构信号还是比较困难的; 而随着SNR值的提高, 即干扰信号逐渐减弱, 可以看到重构效果逐渐变好, COCLMP算法相对于其他4种算法其抗噪的性能提升更明显.进一步提高采样阶段的SNR值, 其重构效果提升较缓慢, 这是因为这一阶段噪声相对较弱, 算法重构能力趋于稳定.
图 2 噪声干扰的不同采样次数下OMP、StOMP、CoSaOMP、ROMP、COCLMP算法重构结果Fig. 2 Reconstruction result include noise under different sampling number for OMP, StOMP, CoSaOMP, ROMP, COCLMP5.2 对噪声图像的重构
本节通过噪声下对图像压缩采样重构性能的研究, 进一步分析本文提出的COCLMP算法与其他算法在重构过程中的抗噪能力.本节选用的噪声为高斯噪声, $\sigma $表示标准方差, 用PSNR (Peak signal to noise ratio)表示重构图像的信噪比[18].
其表达式如下:
$ \begin{equation} {{\rm PSNR} = 10 \times {\lg }\left( {\frac{{{{\left( {{2^n} - 1} \right)}^2}}}{{\rm MSE}}} \right)} \end{equation} $
(38) 其中, MSE是原图像与处理图像之间均方误差. Peak就是指8 bits表示法, 最大值255. MSE指Mean square error, PSNR的单位为dB. PSNR值越大, 就代表失真越少[19]. 5种算法在不同标准方差下的重构效果如图 3所示.
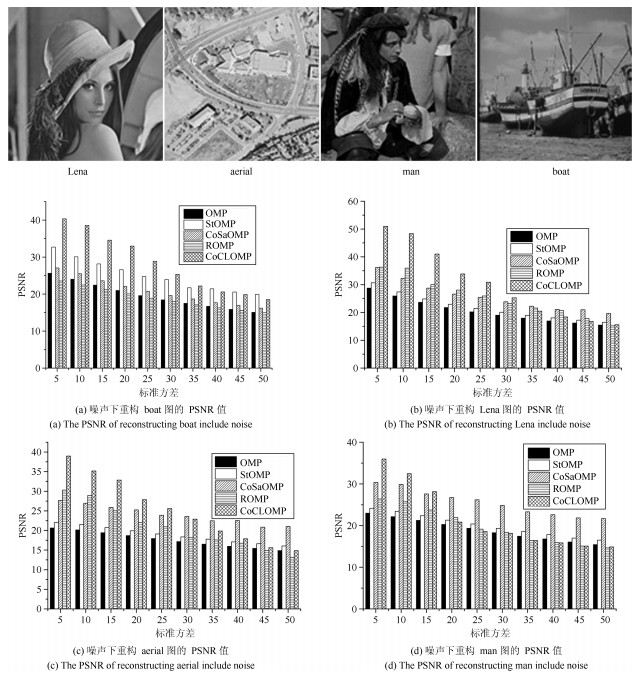
图 3 噪声干扰下OMP、StOMP、CoSaOMP、ROMP、COCLMP算法对图像的重构效果Fig. 3 Image reconstruction effect include noise for OMP, StOMP, CoSaOMP, ROMP, COCLMP图 3中展示了在增加的噪声标准方差为10、20、30、40、50情况下, OMP、StOMP、CoSaOMP、ROMP、COCLMP算法对图像的重构效果.从图 3中可以看出, 随着噪声强度的增加, 重构效果逐渐变差, 特别是在噪声的标准方差为50的情况下, 各种算法重构效果差异不大.但在噪声强度不太高的情况下, 即标准方差为5到30之间, 可以看出相比于其他算法, COCLMP算法重构的图像效果更好, 由此表明COCLMP对于低噪声环境对图像进行压缩采样后的重构能力优于其他4种匹配追踪算法.为了更好分析本文提出的COCLMP算法的性能, 实验进一步采用了数字图像处理标准测试图库Lena、aerial、man、boat图.
图 4进一步列举出了在噪声的标准方差为$5, 10, \cdots, 50$情况, 这5种算法重构Lena、aerial、man、boat图的峰值信躁比(PSNR).从图 4中可以观察到在噪声的标准方差为5, 10, $\cdots, $ 30时, COCLMP算法重构图像的PSNR值都高于其他4种算法, 而在噪声强度较高的30, 35, $\cdots, $ 50区间, COCLMP算法并没表现出明显优势, 这与图 4展示的结果一致.也进一步说明了COCLMP算法对低能噪声干扰下进行压缩采样后的重构能力具有较大的提升.但由于COCLMP算法在每次迭代过程中需要进行解序列的优化选择, 且其选择的权重$w$的本身又是一个最优化问题, 其计算复杂较高, 因此算法收敛的时间相比其他算法时间较长, 对于进行实时的信号处理还需要进一步提高计算效率.
图 4 噪声下重构Lena、aerial、man、boat图的PSNRFig. 4 The PSNR of reconstructing Lena, aerial, man, boat include noise以上实验从信号和图像的角度对COCLMP算法进行测试, 从结果中可以分析出COCLMP算法同其他4种重构算法在无噪声的环境下, 重构能力基本相当.其性能差异主要体现在当压缩采样受到噪声干扰的情况下, COCLMP算法的重构效果好于其他4种算法.当然这种较好的重构能力, 在低能噪声干扰下表现得突出, 而对于高噪声影响, 由于本身压缩采样就是欠采样, 所以采样数据本身受影响过大, 较难实现精确重构.
6. 结论
在本文中, 我们提出一种基于CGLS和LSQR的联合优化的匹配追踪算法.该算法根据匹配追踪系列算法需要解最小二乘问题这一特点, 利用CGLS算法和LSQR算法产生该问题的两组解序列.用上一步的解序列作为下一步LSQR和CGLS算法的输入产生新解序列, 然后通过Alpha散度选择较优解序列, 作为下一次LSQR和CGLS算法的输入, 不断迭代, 直到满足收敛条件.该算法在噪声环境下的压缩感知的重构过程表现出较好的性能.实验表明在高斯噪声下这种联合优化的匹配追踪算法对低噪声具有较好重构效果.
-
Table 1
Algorithm 1 Stepwise iterative algorithm Step 1. Given an initial predictive control sequence $\overline{U}_0$ and a threshold $\lambda$. Step 2. Calculate $J_{\rm old}(k)$ by using $\overline{U}_0$. Step 3. Determine the communication delay $k_t$ in the feedback channel. For the forward communication delay $i=0, 1, \ldots, \overline{M}$: Step 3.1 Calculate $K_i$ according to (12); Step 3.2 Calculate $V_i$ according to (13); Step 3.3 Calculate $u^{\star}_{t+i|t-k_t}$ according to (15). Step 4. Calculate $J_{\rm new}(k)$ by using the obtained $\overline{U}^{\star}_{t+\overline{M}}$. Step 5. If $[J_{\rm old}(k)-J_{\rm new}(k)]/J_{\rm old}(k)>\lambda$, let $J_{\rm old}(k)=J_{\rm new}(k), $ $\overline{U}_0=\overline{U}^{\star}_{t+\overline{M}}$, and go to Step 3; Otherwise, stop iterating and let $\overline{U}^{\star}_{t+\overline{M}}$ as the final optimal predictive control sequence. 
下载: 导出CSV
Table 2
Algorithm 2 Approximate forward stagewise algorithm Step 1. Calculate $u^{\star}_{t|t-k_t}$ according to Remark 8 for the case of no delay in the forward channel. Step 2. For the forward communication delay $i_t=1, 2, \ldots, \overline{M}$: Step 2.1 Add $\hat{x}^T_{t+i_t+1|t-k_t}$ into state vector $\overline{X}$; Step 2.2 Add $u_{t+i_t|t-k_t}$ into input vector $\overline{U}$; Step 2.3 Extend matrixes $Q_{k_t, 0}$ and $R_{k_t, 0}$ to the corresponding dimensions; Step 2.4 Calculate $\overline{K}_{i_t}$ and $\overline{V}_{i_t}$ according to (17) and (18); Step 2.5 Obtain $\overline{U}^{\star}_{k_t, i_t}$ according to (20). Step 3. Take $\overline{U}^{\star}_{\overline{N}, \overline{M}}$ as the final predictive control sequence and send it to the actuator via the forward channel.
下载: 导出CSV
-
[1] R. A. Gupta and M. Y. Chow, "Networked control system:overview and research trends, " IEEE Trans. Ind. Electron., vol.57, no.7, pp.2527-2535, Nov.2010. https://www.researchgate.net/publication/224076713_Networked_Control_System_Overview_and_Research_Trends [2] W. P. M. H. Heemels, A. R. Teel, N. van de Wouw, and D. Nesic, "Networked control systems with communication constraints:tradeoffs between transmission intervals, delays and performance, " IEEE Trans. Autom. Control, vol.55, no. 8, pp.1781-1796, Feb.2010. https://www.researchgate.net/publication/224112751_Networked_Control_Systems_With_Communication_Constraints_Tradeoffs_Between_Transmission_Intervals_Delays_and_Performance [3] R. N. Yang, P. Shi, G. P. Liu, and H. J. Gao, "Network-based feedback control for systems with mixed delays based on quantization and dropout compensation, " Automatica, vol.47, no.12, pp.2805-2809, Dec.2011. http://www.sciencedirect.com/science/article/pii/S000510981100433X [4] M. F. Ren, J. H. Zhang, M. Jiang, and J. L. Xu, "Minimum (h, φ)-entropy control for non-Gaussian stochastic networked control systems and its application to a networked DC motor control system, " IEEE Trans. Control Syst. Technol., vol.23, no.1, pp.406-411, Jan.2015. https://www.researchgate.net/publication/280235329_Minimum_Entropy_Control_for_Non-Gaussian_Stochastic_Networked_Control_Systems_and_Its_Application_to_a_Networked_DC_Motor_Control_System [5] G. Nikolakopoulos, L. Dritsas, and S. S. Delshad, "Combined networked switching output feedback control with D-region stability for performance improvement, " Int. J. Control, vol.87, no.6, pp.1172-1180, Jun.2014. https://www.researchgate.net/publication/263495014_Combined_networked_switching_output_feedback_control_with_Inline_graphic-region_stability_for_performance_improvement [6] R. Luck and A. Ray, "Experimental verification of a delay compensation algorithm for integrated communication and control systems, " Int. J. Control., vol.59, no.6, pp.1357-1372, 1994. doi: 10.1080/00207179408923135 [7] H. J. Gao and T. W. Chen, "Network-based output tracking control, " IEEE Trans. Autom. Control, vol.53, no.3, pp.655-667, Apr.2008. https://www.researchgate.net/publication/3033073_Network-Based_Output_Tracking_Control [8] G. P. Liu, J. X. Mu, and D. Rees, "Networked predictive control of systems with random communication delay, " in Proc. UKACC Control, Bath, U. K. , 2004. [9] G. P. Liu, "Predictive controller design of networked systems with communication delays and data loss, " IEEE Trans. Circuits Syst. Ⅱ Exp. Briefs, vol.57, no.6, pp.481-485, Jun. 2010. https://www.researchgate.net/publication/224142479_Predictive_Controller_Design_of_Networked_Systems_With_Communication_Delays_and_Data_Loss [10] Y. Q. Xia, W. Xie, B. Liu, and X. Y. Wang, "Data-driven predictive control for networked control systems, " Inf. Sci., vol. 235, pp.45-54, Jun.2013. http://www.sciencedirect.com/science/article/pii/S0020025512000758 [11] Z. H. Pang, G. P. Liu, and D. H. Zhou, "Design and performance analysis of incremental networked predictive control systems, " IEEE Trans. Cyber., vol.46, no.6, pp.1400-1410, Jun. 2016. https://www.researchgate.net/publication/280116504_Design_and_Performance_Analysis_of_Incremental_Networked_Predictive_Control_Systems [12] J. H. Zhang, J. Lam, and Y. Q. Xia, "Output feedback delay compensation control for networked control systems with random delays, " Inf. Sci., vol.265, pp.154-166, May2014. http://www.sciencedirect.com/science/article/pii/S0020025513008712 [13] G. P. Liu, J. X. Mu, D. Rees, and S. C. Chai, "Design and stability analysis of networked control systems with random communication time delay using the modified MPC, " Int. J. Control, vol. 79, no. 4, pp. 288-297, 2006. doi: 10.1080/00207170500533288 [14] J. X. Mu, G. P. Liu, and D. Rees, "Design of robust networked predictive control systems, " in Proc. 2005 American Control Conf. , Portland, OR, USA, vol. 1, pp. 638-643, 2005. https://www.researchgate.net/publication/4151220_Design_of_robust_networked_predictive_control_systems?ev=sim_pub [15] R. R. Mohler, Bilinear Control Processes:with Applications to Engineering, Ecology and Medicine, Orlando:Academic Press, 1973. [16] G. Marchesini and S. K. Mitter, Mathematical Systems Theory, Berlin Heidelberg:Springer, 1976. [17] Y. B. Zhao, G. P. Liu, and D. Rees, "A predictive control-based approach to networked Hammerstein systems:design and stability analysis, " IEEE Trans. Syst. Man Cybern. B, Cybern., vol.38, no.3, pp.700-708, Jun.2008. https://www.ncbi.nlm.nih.gov/pubmed/18558535/# [18] Y. B. Zhao, G. P. Liu, and D. Rees, "A predictive control based approach to networked wiener systems, " Int. J. Innov. Comput. Inf. Control., vol.4, no.11, pp.2793-2802, Nov. 2008. https://www.researchgate.net/publication/264840709_A_predictive_control_based_approach_to_networked_wiener_systems [19] H. Ouyang, G. P. Liu, D. Rees, and W. Hu, "Predictive control of networked non-linear control systems, " Proc. Inst. Mech. Eng. J. Syst. Control Eng., vol.221, no.3, pp.453-463, May2007. https://www.researchgate.net/publication/245389365_Predictive_control_of_networked_non-linear_control_systems [20] G. Pin and T. Parisini, "Networked predictive control of uncertain constrained nonlinear systems:recursive feasibility and input-to-state stability analysis, " IEEE Trans. Autom. Control, vol.56, no.1, pp.72-87, Jan.2011. https://www.researchgate.net/publication/220387079_Networked_Predictive_Control_of_Uncertain_Constrained_Nonlinear_Systems_Recursive_Feasibility_and_Input-to-State_Stability_Analysis [21] G. P. Liu, "Design and analysis of networked non-linear predictive control systems, " IET Control Theory Appl., vol.9, no.11, pp.1740-1745, Jul.2015. [22] P. E. Gill and E. Wong, "Sequential quadratic programming methods", in Mixed Integer Nonlinear Programming, J. Lee and S. Leyffer, Eds. , New York, USA, Springer, 2012. [23] M. Hotz and C. Vogel, "Linearization of time-varying nonlinear systems using a modified linear iterative method, " IEEE Trans. Signal Process., vol.62, no.10, pp.2566-2579, May 2014. http://www.oalib.com/paper/4081839 [24] A. Bidram, F. L. Lewis, and A. Davoudi, "Synchronization of nonlinear heterogeneous cooperative systems using input-output feedback linearization, " Automatica., vol.50, no.10, pp.2578-2585, Oct.2014. http://dl.acm.org/citation.cfm?id=2941006.2941225 [25] Z. L. Mu, F. Liu, and Z. L. Qiu, "Analysis of stabilizing control of discrete bilinear system, " Control Theory Appl., vol.17, no.2, pp.267-269, Apr.2000. http://en.cnki.com.cn/Article_en/CJFDTOTAL-KZLY200002025.htm 期刊类型引用(4)
1. 郭俊锋，胡婧怡，王智明. 基于压缩感知的缺失机械振动信号重构新方法. 振动与冲击. 2024(10): 197-204 . 
百度学术2. 田占峰，裴世建，于强. 复杂岩溶地区跨孔地震CT反演成像研究——以贵阳在建地铁3号线为例. CT理论与应用研究. 2024(05): 561-567 . 百度学术3. 焦帆，曹余庆，谢莉. 时滞和阶次未知的双率采样输出误差系统辨识. 控制与决策. 2024(09): 3006-3012 . 百度学术4. 王金甲，张玉珍，夏静，王凤嫔. 多层局部块坐标下降法及其驱动的分类重构网络. 自动化学报. 2020(12): 2647-2661 . 本站查看其他类型引用(6)
-
下载:
计量
- 文章访问数: 2223
- HTML全文浏览量: 201
- PDF下载量: 632
- 被引次数: 10
