Guaranteed Consensus Control of Mobile Sensor Networks With Partially Unknown Switching Probabilities
-
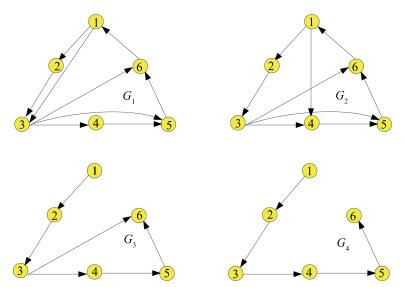
摘要: 本文研究了基于马尔科夫切换拓扑的移动传感网保性能一致性问题.网络拓扑切换由一般的马尔科夫链驱动,其初始和转移概率部分未知.切换拓扑集中的每个拓扑皆是带有树的有向拓扑图.借助定义包括接收、发送信息和控制输入的新的全局能耗函数,可以得到切换分布式一致性控制器集合.然后经过状态变换,一致性控制问题转化为减阶的马尔科夫跳跃系统的保性能问题.通过分析马尔科夫跳跃系统的稳定性,提出了可以同时计算次优的一致性控制器增益和次小能耗上界的算法.最后,通过数值仿真检验了控制器设计方法的性能.Abstract: This paper studies the guaranteed consensus of mobile sensor networks (MSNs) with stochastic switching topologies. The switching of topology is triggered by a Markov chain, whose initial and transition probabilities are partially unknown. Each topology in the switching topology set is a directed graph with a spanning tree. A set of distributed switching consensus controllers are derived by means of stability analysis of Markovian jump systems. This is achieved by defining a novel topology-aware cost function of the MSNs involving cost consumption for information receiving, sending and control. By state transformation, the initial dynamics of MSN is reduced to a Markovian jump system with guaranteed cost. A computational algorithm is proposed to simultaneously calculate both the sub-optimal controller gains and the sub-minimal upper cost bound. Eventually, the performance of the controller design method is verified by numerical examples.
-
Key words:
- Mobile sensor networks (MSNs) /
- Markov switching topologies /
- mean-square consensus /
- guaranteed cost control
-
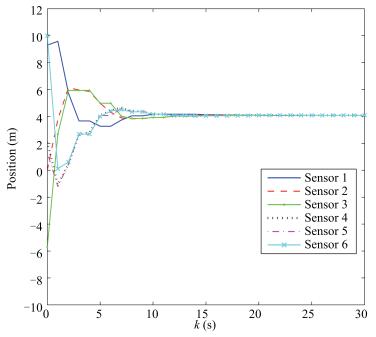
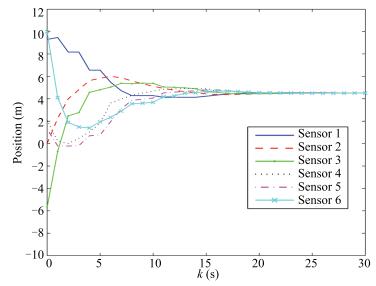
Fig. 4 Positions of the nodes in the MSN with controller design method in [30].
Algorithm 1. Step 1: Set the initial state $x_i (0)$ $(i=1, {\ldots}, N)$ , weight matrices $Q1, Q2$ , $R$ and the computational accuracy $\varepsilon $ . Let $e=0$ . Step 2: Find a feasible solution $\bar {\delta }$ of $\delta $ by solving (38), set $f=\bar {\delta }$ . Step 3: Let g=(e+f)/2, $\delta =g$ . Solving (38), if there exist feasible the solutions $K_l $ ( $l\in S)$ , set $f=g$ . Otherwise, $e=g$ . Step 4: If $\left| {e-f} \right|<\varepsilon $ , output $\delta $ and $K_l $ . Otherwise, go to Step 3. -
[1] J. P. He, H. Li, J. M. Chen, and P. Cheng, "Study of consensus-based time synchronization in wireless sensor networks, " ISA Trans. , vol. 53, no. 2, pp. 347-357, Mar. 2014. http://www.ncbi.nlm.nih.gov/pubmed/24287323 [2] S. Y. Zhao, B. M. Chen, and T. H. Lee, "Optimal deployment of mobile sensors for target tracking in 2D and 3D spaces, " IEEE/CAA J. Autom. Sinica, vol. 1, no. 1, pp. 24-30, Jan. 2014. https://www.researchgate.net/publication/289162749_Optimal_deployment_of_mobile_sensors_for_target_tracking_in_2D_and_3D_spaces?ev=auth_pub [3] G. L. Wang, G. H. Cao, and T. F. La Porta, "Movement-assisted sensor deployment, " IEEE Trans. Mob. Comput. , vol. 5, no. 6, pp. 640-652, Jun. 2006. http://www.researchgate.net/publication/3436516_Movement-Assisted_Sensor_Deployment [4] S. G. Zhang, J. N. Cao, L. J. Chen, and D. X. Chen, "Accurate and energy-efficient range-free localization for mobile sensor networks, " IEEE Trans. Mob. Comput. , vol. 9, no. 6, pp. 897-910, Jun. 2010. http://www.researchgate.net/publication/220466350_Accurate_and_Energy-Efficient_Range-Free_Localization_for_Mobile_Sensor_Networks [5] N. Heo and P. K. Varshney, "Energy-efficient deployment of intelligent mobile sensor networks, " IEEE Trans. Syst. Man Cybern. A Syst. Hum. , vol. 35, no. 1, pp. 78-92, Jan. 2005. https://www.researchgate.net/publication/3412403_Energy-efficient_deployment_of_Intelligent_Mobile_sensor_networks [6] C. Song, G. Feng, Y. Wang, and Y. Fan, "Rendezvous of mobile agents with constrained energy and intermittent communication, " IET Control Theory Appl. , vol. 6, no. 10, pp. 1557-1563, Jul. 2012. https://www.researchgate.net/publication/260586809_rendezvous_of_mobile_agents_with_constrained_energy_and_intermittent_communication [7] Z. Hong, R. Wang, and X. L. Li, "A clustering-tree topology control based on the energy forecast for heterogeneous wireless sensor networks, " IEEE/CAA J. Autom. Sinica, vol. 3, no. 1, pp. 68-77, Jan. 2016. https://www.researchgate.net/publication/302986010_A_clustering-tree_topology_control_based_on_the_energy_forecast_for_heterogeneous_wireless_sensor_networks [8] A. Razavi, W. B. Zhang, and Z. Q. Luo, "Distributed optimization in an energy-constrained network: analog versus digital communication schemes, " IEEE Trans. Inf. Theory, vol. 59, no. 3, pp. 1803-1817, Mar. 2013. https://www.researchgate.net/publication/220734594_Distributed_optimization_in_an_energy-constrained_network_using_a_digital_communication_scheme [9] L. Xia and B. Shihada, "Decentralized control of transmission rates in energy-critical wireless networks, " in Proc. 2013 American Control Conference, Washington, DC, USA, 2013, pp. 113-118. https://www.researchgate.net/publication/261433040_Decentralized_control_of_transmission_rates_in_energy-critical_wireless_networks [10] W. Yang and H. B. Shi, "Sensor selection schemes for consensus based distributed estimation over energy constrained wireless sensor networks, " Neurocomputing, vol. 87, pp. 132-137, Jun. 2012. https://www.researchgate.net/publication/257352106_Sensor_selection_schemes_for_consensus_based_distributed_estimation_over_energy_constrained_wireless_sensor_networks [11] S. Coogan, L. J. Ratliff, D. Calderone, C. Tomlin, and S. S. Sastry, "Energy management via pricing in LQ dynamic games, " in Proc. 2013 American Control Conference, Washington DC, USA, 2013, pp. 443-448. https://www.researchgate.net/publication/261347327_Energy_management_via_pricing_in_LQ_dynamic_games [12] Y. C. Cao and W. Ren, "Optimal linear-consensus algorithms: an LQR perspective, " IEEE Trans. Syst. Man Cybern. B Cybern. , vol. 40, no. 3, pp. 819-830, Jun. 2010. https://www.researchgate.net/publication/38062186_Optimal_linear-consensus_algorithms_an_LQR_perspective [13] G. Guo, Y. Zhao, and G. Q. Yang, "Cooperation of multiple mobile sensors with minimum energy cost for mobility and communication, " Inf. Sci. , vol. 254, pp. 69-82, Jan. 2014. https://www.researchgate.net/publication/262325958_Cooperation_of_multiple_mobile_sensors_with_minimum_energy_cost_for_mobility_and_communication [14] G. Guo, "Linear systems with medium-access constraint and Markov actuator assignment, " IEEE Trans. Circuits Syst. I Regul. Pap. , vol. 57, no. 11, pp. 2999-3010, Nov. 2010. https://www.researchgate.net/publication/220625338_Linear_Systems_With_Medium-Access_Constraint_and_Markov_Actuator_Assignment [15] G. Yin, Y. Sun, and L. Y. Wang, "Asymptotic properties of consensus-type algorithms for networked systems with regime-switching topologies, " Automatica, vol. 47, no. 7, pp. 1366-1378, Jul. 2011. https://www.researchgate.net/publication/220156840_Asymptotic_properties_of_consensus-type_algorithms_for_networked_systems_with_regime-switching_topologies [16] C. D. Liao and P. Barooah, "Distributed clock skew and offset estimation from relative measurements in mobile networks with Markovian switching topology, " Automatica, vol. 49, no. 10, pp. 3015-3022, Oct. 2013. [17] Y. P. Gao, J. W. Ma, M. Zuo, T. Q. Jiang, and J. P. Du, "Consensus of discrete-time second-order agents with time-varying topology and time-varying delays, " J. Franklin Inst. , vol. 349, no. 8, pp. 2598-2608, Oct. 2012. https://www.researchgate.net/publication/256710857_consensus_of_discrete-time_second-order_agents_with_time-varying_topology_and_time-varying_delays [18] W. N. Zhou, J. P. Mou, T. B. Wang, C. Ji, and J. A. Fang, "Target-synchronization of the distributed wireless sensor networks under the same sleeping-awaking method, " J. Franklin Inst. , vol. 349, no. 6, pp. 2004-2018, Aug. 2012. https://www.researchgate.net/publication/256711383_Target-synchronization_of_the_distributed_wireless_sensor_networks_under_the_same_sleepingawaking_method?ev=auth_pub [19] A. Tahbaz-Salehi and A. Jadbabaie, "A necessary and sufficient condition for consensus over random networks, " IEEE Trans. Autom. Control, vol. 53, no. 3, pp. 791-795, Apr. 2008. https://www.researchgate.net/publication/3032810_A_Necessary_and_Sufficient_Condition_for_Consensus_Over_Random_Networks [20] M. Akar and R. Shorten, "Distributed probabilistic synchronization algorithms for communication networks, " IEEE Trans. Autom. Control, vol. 53, no. 1, pp. 389-393, Feb. 2008. https://www.researchgate.net/publication/3033000_Distributed_Probabilistic_Synchronization_Algorithms_for_Communication_Networks [21] Y. Zhao, G. Guo, and L. Ding, "Guaranteed cost control of mobile sensor networks with Markov switching topologies, " ISA Trans. , vol. 58, pp. 206-213, Sep. 2015. https://www.researchgate.net/publication/278742569_Guaranteed_cost_control_of_mobile_sensor_networks_with_Markov_switching_topologies [22] Z. B. Lu and G. Guo, "Control with sensors/actuators assigned by Markov chains: transition rates partially unknown, " IET Control Theory Appl. , vol. 7, no. 8, pp. 1088-1097, May2013. https://www.researchgate.net/publication/260586299_Control_with_sensorsactuators_assigned_by_Markov_chains_transition_rates_partially_unknown [23] W. X. Cui, S. Y. Sun, J. A. Fang, Y. L. Xu, and L. D. Zhao, "Finite-time synchronization of Markovian jump complex networks with partially unknown transition rates, " J. Franklin Inst. , vol. 351, no. 5, pp. 2543-2561, May2014. https://www.researchgate.net/publication/261564374_Finite-time_synchronization_of_Markovian_jump_complex_networks_with_partially_unknown_transition_rates [24] L. X. Zhang and E. K. Boukas, "Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities, " Automatica, vol. 45, no. 2, pp. 463-468, Feb. 2009. https://www.researchgate.net/publication/222657436_Stability_and_stabilization_of_Markovian_jump_linear_systems_with_partly_unknown_transition_probability [25] J. L. Xiong, J. Lam, H. J. Gao, and D. W. C. Ho, "On robust stabilization of Markovian jump systems with uncertain switching probabilities, " Automatica, vol. 41, no. 5, pp. 897-903, May2005. https://www.researchgate.net/publication/222248877_On_robust_stabilization_of_Markovian_jump_systems_with_uncertain_switching_probabilities [26] C. S. Zhu, L. Shu, T. Hara, L. Wang, S. Nishio, and L. T. Yang, "A survey on communication and data management issues in mobile sensor networks, " Wirel. Commun. Mob. Comp. , vol. 14, no. 1, pp. 19-36, Jan. 2014. https://www.researchgate.net/publication/259543714_A_survey_on_communication_and_data_management_issues_in_mobile_sensor_networks?ev=auth_pub [27] E. Yaz, "Control of randomly varying systems with prescribed degree of stability, " IEEE Trans. Autom. Control, vol. 33, no. 4, pp. 407-410, Apr. 1988. https://www.researchgate.net/publication/3021303_Control_of_randomly_varying_systems_with_prescribed_degree_of_stability [28] O. L. V. Costa, M. D. Fragoso, and R. P. Marques, Discrete-time Markov Jump Linear Systems. London:Springer-Verlag, 2005. [29] J. H. Qin, H. J. Gao, and C. B. Yu, "On discrete-time convergence for general linear multi-agent systems under dynamic topology, " IEEE Trans. Autom. Control, vol. 59, no. 4, pp. 1054-1059, Apr. 2014. https://www.researchgate.net/publication/261028530_On_Discrete-Time_Convergence_for_General_Linear_Multi-Agent_Systems_Under_Dynamic_Topology [30] Y. B. Hu, J. Lam, and J. L. Liang, "Consensus control of multi-agent systems with missing data in actuators and Markovian communication failure, " Int. J. Syst. Sci. , vol. 44, no. 10, pp. 1867-1878, Oct. 2013. https://www.researchgate.net/publication/254320581_Consensus_control_of_multi-agent_systems_with_missing_data_in_actuators_and_Markovian_communication_failure?ev=auth_pub -




 下载:
下载: