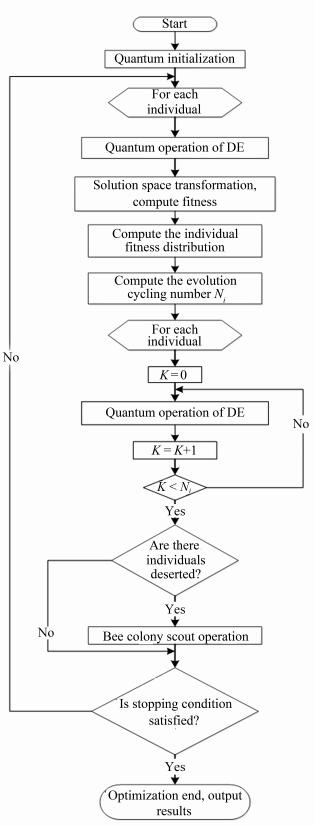
An Improved Quantum Differential Evolution Algorithm for Optimization and Control in Power Systems Including DGs
-
Abstract: Differential evolution algorithm (DE) has been proved to be an effective way for solving the optimal reactive power flow (ORPF) problem. As distributed generations (DGs) are introduced into the system, there is a certain impact on power flow and voltage of the power system, which affects the robustness and effectiveness of DE. On the basis of DE, aiming at its limitation of premature convergence and poor search ability, this paper discusses about how to improve it with quantum encoding and artificial bee colony (ABC) algorithm and proposes a hybrid algorithm, which is called improved quantum differential evolution algorithm (IQDE). The idea of quantum encoding increases the individual diversity while the accelerating evolution operation of the onlooker bees improves local search ability of DE. At the same time, the random search operation of the scout bees improves global search ability of DE. In the last, the effectiveness of IQDE is verified by simulations on the IEEE 14-bus system and 30-bus system including DGs. The experimental results show that with less convergence time and smaller population size, IQDE can obtain an even or better optimization effect compared with DE and can be applied to ORPF problem of power system including DGs.
-
Key words:
- Artificial bee colony /
- differential evolution /
- optimal reactive power flow /
- quantum /
- distributed generation (DG)
摘要: 差分进化算法(DE)已被证明为解决无功优化问题的有效方法.随着越来越多的分布式电源并网,对配电网潮流、电压均有一定改变,同时也影响了DE的鲁棒性和性能.本文在研究DE基础上,针对其收敛过早、局部搜索能力较差的缺陷,分析了量子计算思想和人工蜂群算法的优势,提出改进量子差分进化混合算法(IQDE).通过量子编码思想提高了种群个体的多样性,人工蜂群算法的观察蜂加速进化操作和侦查蜂随机搜索操作分别提高了算法的局部搜索和全局搜索性能.建立以有功网损最小为目标的数学模型,将IQDE算法和DE算法分别用于14节点和30节点标准数据集进行大量仿真实验.实验结果表明,IQDE算法用更少的收敛时间、更小的种群规模便可以获得与DE算法相同甚至更佳的优化效果,并且可以很好的应用于解决难分布式电源的配电网无功优化问题. -
Solar thermal power generation system is affected by natural factors such as solar radiation, and also the system has strong interference. These uncertain factors directly affect the quality of solar thermal power generation. Regulating the tracking error of output oil temperature of collector is an important control objective, therefore it has practical significance to study the active fault tolerant predictive control of solar collector system in the state of fault or disturbance.
The solar collector system uses the solar radiation to heat the heat conduction oil, regulates the flow of heat conduction oil, and controls the outlet temperature of the heat conduction oil in a certain range so as to ensure the stability of the power generation. The control objective of the collection system is that the amount of the actual output is as close as possible to the amount of the desired target output. In recent years, many kinds of intelligent control algorithms are applied to the control of solar thermal power generation system [1]-[3]. Reference [4]-[7] all applied the model predictive control algorithm, where the control target was to minimize the tracking error.
Error of the outlet temperature and the single model are used to predict the model. Multi-model adaptive switching active fault tolerant control is about selecting the model with least cumulative error to determine which model of multi-models is the best match for the dynamic behavior of the system online, and continuously optimize the model parameters. The adaptive model which can be reassigned is used to compensate for the missing data in the process of modeling and to reduce the tracking error with strong disturbance or fault conditions. The algorithm has been successfully applied to other areas [8]-[10], the control effect is good. Based on the above analysis, the main research contents of this paper include:
1) Establish multi-model set. Collect data sets for several consecutive days to make the fuzzy C-means (FCM) clustering.
2) Design active fault tolerant sliding mode predictive controller. Determine the adaptive switching strategy. The inlet temperature and solar radiation are considered as disturbance, and flow of heat conduction oil is considered as controlled variable. Based on the multi-model, the adaptive model of the solar collector system is established to adapt the object and the disturbance characteristics. A model switching strategy based on the minimum cumulative error is used to select the optimal control model online.
3) The method is applied to the actual linear Fresnel power generation system, and the method is compared with [3]. The method in this paper is better than the method [3], the control precision is higher, and the time delay is shorter.
1. Dynamic Model of Solar Thermal Power Generation System
1.1 The Mathematical Model of Micro-sources
1.1.1 Microturbine Cost
R Carmona, a Spanish scholar, initially used the mathematical model [1] to describe the temperature of heat conduction oil of the solar collector [11], and then the model was used to analyze the thermal system [4]-[6].
$ \begin{align} & {\rho _{\rm{f}}}{C_{\rm{f}}}{A_{\rm{f}}}\frac{{{d}{T_n}(t)}}{{{{d}}t}} = {\eta _{\rm{0}}}{G_1}I(t) - {\rho _{\rm{f}}}{C_{\rm{f}}}v(t)\frac{{{T_n}(t) - {T_{n - 1}}(t)}}{{\Delta x}}, \nonumber\\ & \;\;\;\;\;\;\; n = 1, \ldots, N \end{align} $
(1) where $t$ is time, s; $\Delta x$ is length of the collector tube section; ${\rho _{\rm{f}}}$ is refrigerant density, kg/m $^3$ ; ${C_{\rm{f}}}$ is specific heat capacity, ; ${A_{\rm{f}}}$ is cross section area of pipe; $v(t)$ is conduction heat oil flow, ${\rm m^3}$ /s; $I(t)$ is solar intensity, W/ ${\rm m^2}$ ; ${\rm \eta _0}$ is mirror optical efficiency; ${G_1}$ is the optical aperture of reflector, m; $Tn$ is conduction heat oil temperature of oil pipeline outlet, ℃; $Tn - 1$ is conduction heat oil temperature of oil pipeline outlet, ℃.
Take $\Delta x$ = $L$ , then (1) can be
$ \begin{align} & {\rho _{\rm{f}}}{C_{\rm{f}}}{A_{\rm{f}}}\frac{{{\rm{d}}{T_n}(t)}}{{{\rm{d}}t}} = {\eta _{\rm{0}}}{G_1}I(t) - {\rho _{\rm{f}}}{C_{\rm{f}}}v(t)\frac{{{T_n}(t) - {T_0}(t)}}{L}, \notag\\ & \;\;\;\;\;\;\quad n = 1, \ldots, N \end{align} $
(2) where $L$ is the total length of pipeline of the collection system; $T{}_0(t)$ is the entrance conduction heat oil temperature of collector.
2. Clustering Modeling of Solar Thermal Power Generation Set
2.1 Fuzzy Clustering of Data Set
The data acquisition in the linear Fresnel thermal power generation system is used to make FCM clustering analysis. In this clustering algorithm, the membership degree is used to determine the degree of each element and the measured data is classified by the method of subtraction clustering [12], [13].
Step 1: Determine the number of categories $C$ , fuzzy weight index m and the initial clustering center $v$ ;
Step 2: The fuzzy membership degree ${u_{ij}}$ is calculated according to
$ \begin{align} {u_{ij}} = \begin{cases} {\left[{\sum\limits_{k = 1}^C {\frac{{{{\left\| {{x_i}-{\upsilon _j}} \right\|}^{\frac{2}{{m-1}}}}}}{{{{\left\| {{x_i}-{\upsilon _k}} \right\|}^{\frac{2}{{m - 1}}}}}}} } \right]^{ - 1}}, & \left\| {{x_i} - {\upsilon _k}} \right\| \ne 0\\ 1, & \left\| {{x_i} - {\upsilon _k}} \right\| = 0, ~~{k} = j\\ 0, & \left\| {{x_i} - {\upsilon _k}} \right\| = 0, ~~{k} \ne j. \end{cases} \end{align} $
(3) ${u_{ij}}$ is the fuzzy membership degree of category $J$ of individual. ${\upsilon _j}$ is cluster center of category $J$ .
Step 3: Use (4) to calculate the center of each category.
$ \begin{align} {\upsilon _j} = \frac{{\sum\limits_{i = 1}^n {u_{ij}^m{x_i}} }}{{\sum\limits_{i = 1}^n {u_{ij}^m} }}. \end{align} $
(4) Step 4: The target value is calculated according to (5) to determine whether the values meet the target value or not. If the values meet the target value, the clustering is end. Otherwise, return Step 2.
$ \begin{align} J = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^C {{{({u_{ij}})}^m}\left\| {{x_i} - {\upsilon _j}} \right\|} }. \end{align} $
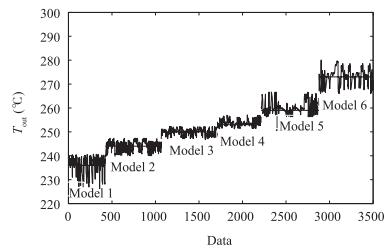
(5) In this paper, DB is used as an evaluation index of the classification [14]. The smaller the index value is, the better the clustering effect is. In this paper, for 3500 sets of actual power generation data $M$ from the solar thermal power generation system of Gansu Lanzhou Dacheng company, which is put into use in Lanzhou New District, $M({m_1}$ , ${m_2}$ , ${m_3}$ , ${m_4}$ ) is classified, among them, ${m_1}$ is the outlet temperature, ${m_2}$ is the heat transfer oil outlet temperature, ${m_3}$ is flow, and the solar radiation is ${m_4}$ . Fuzzy clustering is used to analyze such data. When $C$ = 6, DB is the smallest, and Table Ⅰ lists the clustering results.
表 Ⅰ Clustering ResultsTable Ⅰ Clustering ResultsC 2 3 4 5 6 7 8 9 DB 1.3893 1.0168 0.6306 0.7065 0.1746 0.9135 0.4936 0.6304 The clustering centers of the 6 types are respectively:
$ \begin{align*} & {\upsilon _1} = (\begin{array}{*{20}{c}} {236.6} & {196.0} & {10.15} & {780.5} \end{array})\\ & {\upsilon _2} = (\begin{array}{*{20}{c}} {244.4} & {203.0} & {10.03} & {890.9} \end{array})\\ & {\upsilon _3} = (\begin{array}{*{20}{c}} {250.1} & {210.0} & {10.20} & {916.6} \end{array})\\ & {\upsilon _4} = (\begin{array}{*{20}{c}} {253.6} & {213.4} & {10.32} & {933.0} \end{array})\\ & {\upsilon _5} = (\begin{array}{*{20}{c}} {259.7} & {219.6} & {10.18} & {935.5} \end{array})\\ & {\upsilon _6} = (\begin{array}{*{20}{c}} {273.6} & {232.9} & {10.04} & {953.2} \end{array}). \end{align*} $
2.2 Least-squares Modeling
The above classification data results considered the inlet oil temperature, solar radiation and flow rate of conduction heat oil as input, and outlet temperature as output. In order to overcome the shortcomings of the least squares due to its poor correction ability, forgetting factor recursive least square method is adopted [9], [15], [16]. The controlled auto regressive (CAR) model expressed by formula (6) is used to identify the parameters.
$ \begin{align} y(k) = {{\bf{\varphi }}^T}(k)\hat\theta (k). \end{align} $
(6) where,
$ \begin{align*} & y(k + 1) = [{y_1}(k + 1), {y_2}(k + 1), {y_3}(k + 1), \\ & \;\;\quad {y_4}(k + 1), {y_5}(k + 1), {y_6}(k + 1){]^{{T}}} \\[3mm] & \hat\theta = \left[{\begin{array}{*{20}{c}} {{a_{11}}} & {{a_{12}}} & {{a_{13}}} & {{a_{14}}}\\ {{a_{21}}} & {{a_{22}}} & {{a_{23}}} & {{a_{24}}}\\ {{a_{31}}} & {{a_{32}}} & {{a_{33}}} & {{a_{34}}}\\ {{a_{41}}} & {{a_{42}}} & {{a_{43}}} & {{a_{44}}}\\ {{a_{51}}} & {{a_{52}}} & {{a_{53}}} & {{a_{54}}}\\ {{a_{61}}} & {{a_{62}}} & {{a_{63}}} & {{a_{64}}} \end{array}} \right]\nonumber \\[3mm] & {{ {\varphi }}^T}(k + 1) = \left[{\begin{array}{*{20}{c}} {-{y_1}(k)} & {{u_1}(k)} & {{T_{\rm out}}_1(k)} & {{I_1}(k)}\\ {-{y_2}(k)} & {{u_2}(k)} & {{T_{\rm out2}}(k)} & {{I_2}(k)}\\ {-{y_3}(k)} & {{u_3}(k)} & {{T_{\rm out3}}(k)} & {{I_3}(k)}\\ { - {y_4}(k)} & {{u_4}(k)} & {{T_{\rm out4}}(k)} & {{I_4}(k)}\\ { - {y_5}(k)} & {{u_5}(k)} & {{T_{\rm out5}}(k)} & {{I_5}(k)}\\ { - {y_6}(k)} & {{u_6}(k)} & {{T_{\rm out6}}(k)} & {{I_6}(k)} \end{array}} \right].\nonumber \end{align*} $
Initial value $\theta (0) = 0$ is the positive real vector with zero or small value. The mathematical model of the solar collector system can be obtained, as shown in the model (7).
$\begin{align} \begin{cases} {y_1}(k + 1) = 0.9217{y_1}(k) + 0.3011{u_1}(k)\\ \;\;\quad +~ 0.0701{T_{\rm in}}_1(k) + 0.0015{I_1}(k)\\[2mm] {y_2}(k + 1) = 0.9501{y_2}(k) + 0.2126{u_2}(k)\\ \;\;\quad +~ 0.0631{T_{\rm in2}}(k) + 0.0041{I_2}(k)\\[2mm] {y_3}(k + 1) = 0.9438{y_3}(k) + 0.6421{u_3}(k)\\ \;\;\quad +~ 0.0763{T_{\rm in}}_3(k) + 0.0039{I_3}(k) \\[2mm] {y_4}(k + 1) = 0.9573{y_4}(k) + 0.434{u_4}(k)\\ \;\;\quad +~ 0.0614{T_{\rm in4}}(k) + 0.0032{I_4}(k) \\[2mm] {y_5}(k + 1) = 0.9680{y_5}(k) + 0.3171{u_5}(k)\\ \;\;\quad +~ 0.0549{T_{\rm in5}}(k) + 0.0036{I_5}(k) \\[2mm] {y_6}(k + 1) = 0.9702{y_6}(k) + 0.4021{u_6}(k)\\ \;\;\quad +~ 0.0593{T_{\rm in6}}(k) + 0.0031{I_6}(k) \end{cases} \end{align} $
(7) where ${y_i}(k)$ is output oil temperature, ${u_i}(k)$ is the flow rate of conduction heat oil, ${T_{\rm in}}_{ i}(k)$ is input oil temperature, and ${I_i}(k)$ is solar radiation.
According to the results of the optimal clustering center, the outlet temperature is considered as the center to analyze the error of classification. Fig. 1 shows the effect of deviation of each class of data from the center point of the cluster. In different temperature and cross sectional output data, outlet temperature is also affected by the inlet temperature and solar radiation. Therefore, the system can be considered as a multi disturbance system.
3. Multi-model Active Fault Tolerant Sliding Mode Predictive Controller
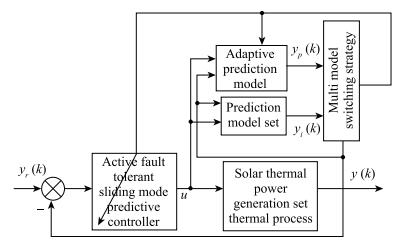
Predictive control includes prediction model, rolling optimization and feedback correction. Under the condition of system fault or disturbance, the multi-model adaptive switching active fault tolerant control can update the control law based on the optimal predictive model online, which results in stable operation of the closed-loop system. In the process of rolling optimization, update control law online, and through the feedback of correction, the error is corrected online. Fig. 2 is the structure of a multi-model active fault tolerant controller of solar thermal power generation. ${y_r}(k)$ is the desired output, $y(k)$ is the actual output of model, ${y_i}(k)$ is the most optimal sub model, and ${y_p}(k)$ is the adaptive model.
In [17]-[19], a single model sliding mode predictive control is designed for the high speed aircraft. In [18], a multi-model sliding mode predictive control is designed for the disturbance signal. Active fault tolerant predictive controller is designed for high-speed train based on [19]. In the literature, the designed controller according to different system has achieved good control effect. By referring to the above documents, this article designed the active fault tolerant control in solar thermal applications. Consider the following uncertain discrete linear systems
$ \begin{align} y(k + 1) - {{{A}}}y(k) = {{{B}}}u(k) + \xi (k) \end{align} $
(8) where $y(k)$ is the output, $u(k)$ $\in \mathbb{R}$ is the control input, $A$ and $B$ are matrixes with appropriate dimension, and is the total interference.
3.1 Sliding Mode Surface Design
Define the switching function: set the reference command signal ${y_r}(k)$ , define the tracking error (9).
$ \begin{align} e(k) = y(k) - {y_r}(k). \end{align} $
(9) Define the linear switching function:
$ \begin{align} s(k) = {\sigma ^{T}}e(k) \end{align} $
(10) where ${\sigma ^{T}} = [{\sigma _1}, \ldots, {\sigma _n}]$ . After the solar collector model expression (2) is discretized, the configuration of poles of the expected oil outlet temperature is set inside the unit circle, and then ${\sigma _i}$ is obtained through the calculation. In order to guarantee the stability and dynamic performance of the ideal sliding mode, construct the following sliding mode prediction model.
$ \begin{align} s(k + 1) = {\sigma ^{T}}e(k + 1). \end{align} $
(11) The predicted sliding mode surface is ${S_m} = \{ e(k)|{s(e(k))}$ $=$ $0\}$ . The p step ahead predictor is as follow.
$ \begin{align} s(k + p) = & \ {\sigma ^{T}}{A^p}y(k)\nonumber\\ & + \sum\limits_{i = 1}^p {{\sigma ^{T}}{A^{p - i}}[} Bu(k + p-i)\nonumber\\ & + \xi (k + p-i)] - {\sigma ^{T}}{y_r}(k + p). \end{align} $
(12) Use the difference value between actual switching function output value $s(k)$ and $p$ step ahead prediction at the moment of $k - p$ to make the feedback correction of output value ${s_p}(k + p)$ of sliding mode prediction model. Thus, the output of the closed-loop sliding mode prediction model can be expressed as:
$ \begin{align} {{\tilde s}_p}(k + p) = s(k + p) + {\zeta _p}[s(k)-{s_p}(k | {k- p})] \end{align} $
(13) where ${\zeta _p} \in \mathbb{R}$ is the weighted feedback correction factor. Let ${\zeta _1}$ $=$ $1$ , $0 < {\zeta _p} < 1$ $(p \ge 1)$ . Decrease of ${\zeta _p}$ can reduce the role of feedback correction.
3.2 Sliding Mode Reference Trajectory
Take the commonly reaching rate as the reference trajectory.
$ \begin{align} \begin{cases} {s_r}(k + p) = \mu {s_r}(k + p - 1) + \eta {\rm sgn} ({s_r}(k + p - 1))\\ {{s_r}(k) = s(k)} \end{cases} \end{align} $
(14) where $0 < \mu < 1, $ $\eta >0$ . The greater the $\mu $ , the smaller the switching power. Control objective is that the error state reaches the sliding mode surface that is to say $s(e(k)) = 0$ .
3.3 Control Law Design
Define the performance index
$ \begin{align} J= \sum\limits_{i = 1}^N {{{({s_r}(k + i) - \tilde s(k + i))}^2}} + \sum\limits_{j = 0}^{M - 1} {{\lambda _j}{u^2}(k + j)} \end{align} $
(15) where $N$ and $M$ are positive integers, which respectively represent the predicted time domain and control time domain, $M$ needs to meet $N< 0 < M, $ $u(k + j) = u(k + M - 1)$ , $M $ $\le$ $j$ $<$ $ N$ , and ${\lambda _j}$ is weight coefficient.
If the output vector is expressed as:
$ \begin{align} & S = {[s(k + 1), \ldots, s(k + N)]^{T}}\;\;\nonumber \\ & {S_r} = {[{s_r}(k + 1), \ldots, {s_r}(k + N)]^{T}}\nonumber \\ & \tilde S = {[{\tilde s_{}}(k + 1), \ldots, \tilde s(k + N)]^{T}}\;\;\;\nonumber \\ & \bar S = {[s(k)-{s_p}(k\left| {k-1} \right.), \ldots, s(k)-{s_p}(k\left| {k - N} \right.)]^{T}}\notag\\ & \ \ = {[\bar S(1), \ldots, \bar S(N)]^{T}}\notag\\ & U = {[u(k), \ldots, u(k + M-1)]^{T}}\notag\\ & F = {[{\sigma ^{T}}A, \ldots, {\sigma ^{T}}{A^N}]^{T}}\; \nonumber \\ & \Xi = {\rm diag}\{ {\zeta _1}, \ldots, {\zeta _N}\} \notag\\ & \Lambda = {\rm diag}\{ {\lambda _1}, \ldots, {\lambda _M}\}\notag\\ & {{\tilde Y}_r} = {[{{\tilde y}_r}(k), \ldots, {{\tilde y}_r}(k + N -1)]^{T}} \nonumber \end{align} $
$ \begin{array}{l} G = \left[{\begin{array}{*{20}{c}} {{\sigma ^T}B} & 0 & \cdots & 0\\ {{\sigma ^T}AB} & {{\sigma ^T}B} & \cdots & 0\\ \vdots & \vdots & \cdots & {{\sigma ^T}B}\\ \vdots & \vdots & \ddots & \vdots \\ {{\sigma ^T}{A^{N-2}}B} & {{\sigma ^T}{A^{N-3}}B} & \cdots & {\sum\limits_{i = 0}^{N-M - 1} {{\sigma ^T}{A^i}B} }\\ {{\sigma ^T}{A^{N - 1}}B} & {{\sigma ^T}{A^{N - 2}}B} & \cdots & {\sum\limits_{i = 0}^{N - M} {{\sigma ^T}{A^i}B} } \end{array}} \right]\\ P = \left[{\begin{array}{*{20}{c}} {{\sigma ^T}} & 0 & \cdots & 0\\ {{\sigma ^T}A} & {{\sigma ^T}} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ {{\sigma ^T}{A^{N-1}}} & {{\sigma ^T}{A^{N-2}}} & \cdots & {{\sigma ^T}} \end{array}} \right] \end{array} $
then (12) and (13) can be represented as a vector form, which can be expressed by (16) and (17).
$ \begin{array}{l} & S = Fe(k) + GU + P{\tilde Y_r}\;\; \end{array} $
(16) $ \begin{align} & \tilde S = S + \Xi \bar S.\;\;\;\; \end{align} $
(17) So, the performance index expressed by(15) can be written as a vector form expressed by (18).
$ \begin{align} J = {(H - GU)^{T}}(H - GU) + \Lambda {U^{T}}U \end{align} $
(18) where ${L_0}=$ $[1, $ $\ldots, 1]^{T}, $ ${L_1} = {[{\gamma ^1}, \ldots, {\gamma ^N}]^{T}}, $ $ 0 $ $< \gamma$ $<$ $1, $ .
Let $\frac{{\partial J(U)}}{{\partial U}} = 0$ , solve the corresponding equations, and the optimal flow rate of $U$ in the collection process is calculated:
$ \begin{align} U = {({G^{T}}G + \Lambda)^{ - 1}}{G^{T}}H. \end{align} $
(19) 3.4 Multi-model Switching Strategy
The switching strategy is to select the optimal control model online [18] for the state of system under the condition of unknown fault or disturbance, and the active fault tolerant predictive control is carried out through the rolling optimization and feedback correction.
At the $k$ th moment, ${e_i}(k) = y(k) - {\hat y_i}(k)$ is the output error between actual output and $i$ $(1 \le i \le P* + 2)$ model. The definition of switching index is shown in (20).
$ \begin{align} {J_i}(k) = \alpha e_i^2(k) + \beta \sum\limits_{j = 1}^L {{\theta ^j}e_i^2(k - j)} \end{align} $
(20) where $\alpha $ is error coefficient at present, $\beta $ error coefficient for historical moment, $\alpha > 0, $ $\beta > 0, $ $\alpha + \beta = 1$ , $L$ is the number of the concerned historical sampled data, and $\theta = 1$ .
3.5 Adaptive Fault-tolerant Control
3.5.1 Active Fault-tolerant Algorithm
Under the condition of system failure or disturbance, the active fault tolerant control can update the control law according to the optimal control model online selection, which can stabilize the closed loop system [19]. Active fault tolerant control is realized by the adaptive model switching.
3.5.2 Adaptive Model Switching
The adaptive model can be used to obtain a faster convergence rate according to the different conditions. According to the model switching strategy, if the initial parameters of the model are the optimal model parameters of the multi-model set, the optimal model can be selected from the current optimal model set and the parameters can be updated with (21). Otherwise, the initial value of the model is reassigned to the minimum cumulative error model parameters, and then the model parameters are updated online through (21). According to the model switching strategy, the obtained optimal model is the adaptive model, which can guarantee the stability of the system and the accuracy of tracking. Parameters are updated as follows [9], [19].
$ \begin{align} \begin{cases} \hat \theta (k) = \hat \theta (k - 1) + K(k)[y(k)-{\varphi ^T}(k)\hat \theta (k- 1)]\\[1mm] K\left( k \right) = \dfrac{{P\left( {k - 1} \right)\varphi \left( k \right)}}{{\lambda + {\varphi ^T}\left( k \right)P\left( {k - 1} \right)\varphi \left( k \right)}}\\[3mm] P(k) = \dfrac{1}{\lambda }\left[I-K(k){\varphi ^T}(k)\right]P(k - 1) \end{cases} \end{align} $
(21) where $\theta (k)$ are the parameters to be identified, $K(k)$ is gain matrix, $\varphi (k)$ is observation matrix, $P(k)$ is covariance matrix, and $\lambda $ is forgetting factor.
4. Simulation Result Analysis
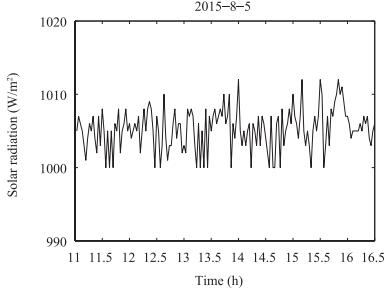
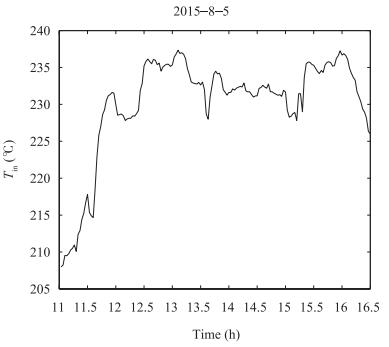
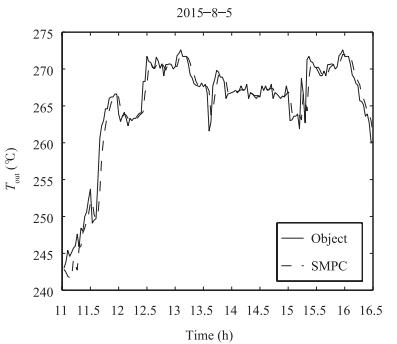
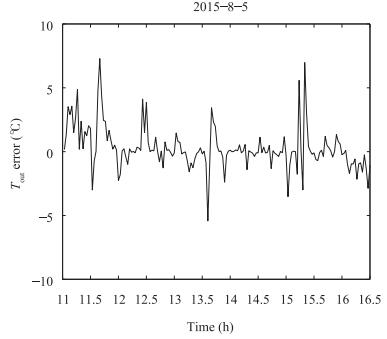
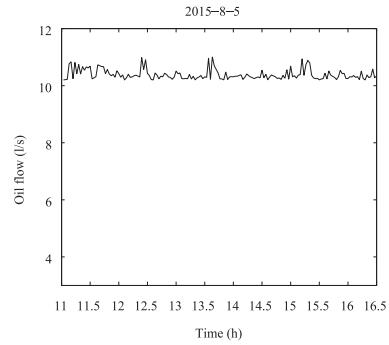
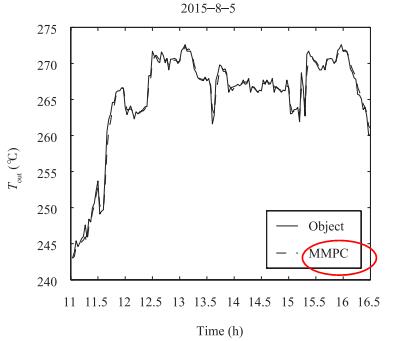
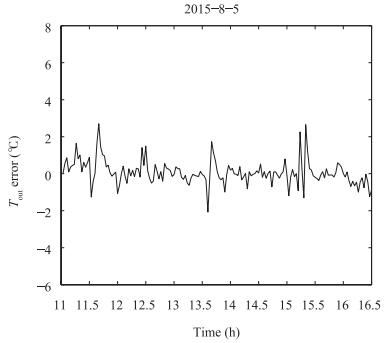
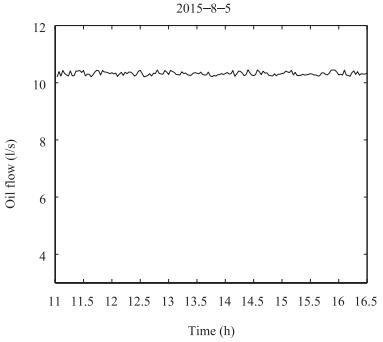
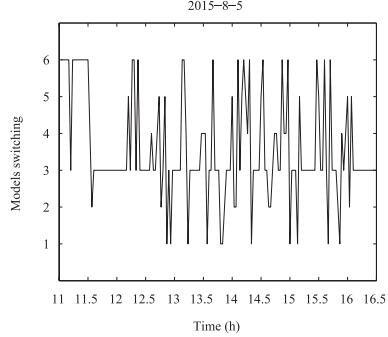
In the process of simulation analysis, system model selects (2). Parameters of the linear Fresnel power generation demonstration project in the west of China are selected and the outlet oil temperature of conducting oil on August 5, 2015 is taken as the target curve. Controlled variable is the flow of heat conduction oil. Inlet oil temperature and solar radiation are disturbances which can be measured. The flow range of heat conduction oil is 3 (l/s)-12 (l/s). ${\eta _0} = 0.60, $ ${C_f}$ $=$ $2600 {\rm J/kg}{^\circ}{\rm C}, $ $T = 20$ s, $L = 220$ m, m $^2$ , $G$ $=$ $0.80$ m. Parameter values of simulation analysis are: $\alpha$ $=$ $0.3, $ $\beta = 0.7$ , $\theta $ is the positive real vector with zero or small initial value, , and forgetting factor $\lambda $ $=$ $0.95$ . Methods in [3] are compared with this paper, the two algorithms simulation results are shown in Fig. 3 to Fig. 8. Fig. 7 and Fig. 10 are the flow of heat conductive oil, and the curve of the control value respectively. Fig. 11 is switching progress between the six models.
The average variance of two kinds of simulation results is analyzed and calculated. MSE = 1.53264 in Fig. 5 and MSE = 0.43276 in Fig. 8.
It can be seen from Fig. 7 and Fig. 10 that multi-model active fault-tolerant sliding mode predictive control is better than that of [3].
5. Conclusion
In this paper, we collected the data of 3500 sets of solar thermal power generation sets, classified them, and set up the mathematical model. A fault-tolerant sliding mode predictive controller is designed, which can reduce error, improve the system's robustness and anti-interference ability. The adaptive prediction model can be used to reduce the error caused by loss of data, the disturbance and fault.
From Fig. 5 and Fig. 8, it can be seen that the method proposed in this paper has higher accuracy and shorter lag time, and has the ability to improve the robustness and convergence rate of the solar thermal power generation system.
-
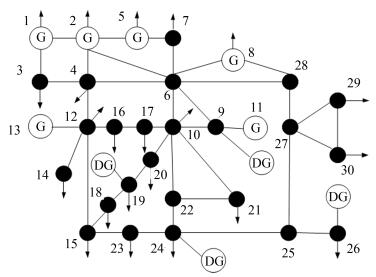
Table Ⅰ Number of Control Variables of IEEE 14-Bus System
Variable Number T 3 U 5 Q 2 SUM 10 Table Ⅱ Setting of Control Variables of IEEE 14-Bus System
Variable Min Max Step T 0.9 1.1 0.01 U 0.9 1.1 - Q 0 0.18 0.06 Table Ⅲ Constraints of The State Variables of IEEE 14-Bus
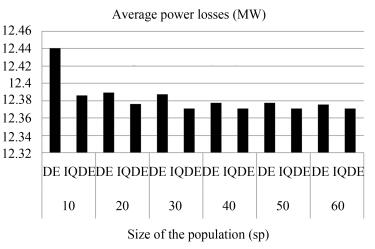
Node Min (MVar) Max (MVar) 1 0 10 2 -40 50 5 -40 40 8 -10 40 11 -6 24 13 -6 24 Table Ⅳ Statistics of Results for DE and IQDE (IEEE 14-Bus)
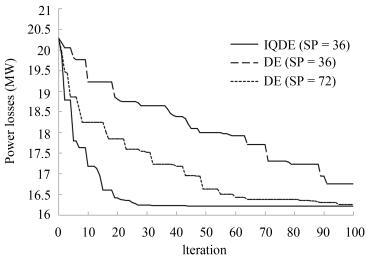
SP Algorithm Lossmin Lossmax Lossavg Timemin Timemax Timeavg 10 DE 12.3714 13.1578 12.4401 3.8977 5.3590 4.9267 IQDE 12.3712 12.5450 12.3858 4.9335 9.0550 7.2024 20 DE 12.3713 12.6364 12.3892 8.7948 9.9069 10.6250 IQDE 12.3712 12.4035 12.3761 7.8281 14.6796 11.2216 30 DE 12.3712 12.549 12.3876 12.569 15.7014 14.8099 IQDE 12.3712 12.3712 12.3712 12.1678 17.7190 14.7212 40 DE 12.3712 12.4463 12.3776 16.6632 21.4070 20.2090 IQDE 12.3712 12.3712 12.3712 15.2144 21.7840 17.3987 50 DE 12.3712 12.4319 12.3774 19.3238 26.4667 25.0056 IQDE 12.3712 12.3712 12.3712 19.0269 26.7894 22.9460 60 DE 12.3712 12.399 12.3754 25.2242 33.3440 30.3782 IQDE 12.3712 12.3712 12.3712 24.4536 33.4038 28.0544 Table Ⅴ Control Variable Setting and PLOSS Before and After Optimization for IEEE 14-Bus System
U1 U2 U3 U6 U8 T4 T5 T7 Q9 Q14 Ploss Before 1.06 1.045 1.01 1.07 1.09 0.978 0.969 0.932 18 18 13.393 After 1.1 1.0779 1.0465 1.1 1.1 1.06 0.9 1.03 18 6 12.3712 Table Ⅵ Number of Control Variables of IEEE 30-Bus System
Variable Number T 4 U 6 Q 2 SUM 12 Table Ⅶ Setting of Control Variables of IEEE 30-Bus System
Variable Minimum Maximum Step T 0.9 1.1 0.02 U 0.9 1.1 - Q9 0 0.2 0.05 Q24 0 0.04 0.01 Table Ⅷ Constraints of the State Variables of 30-Bus
Node Min (MVar) Max (MVar) 1 0 10 2 -40 50 5 -40 40 8 -10 40 11 -6 24 13 -6 24 Table Ⅸ Statistics of Results for DE and IQDE (IEEE 14-Bus)
Node Qout(MVar) Qlow Qup Pout (MW) Plow Pup 9 0.0137 -0.012 0.025 0.15 0.11 0.19 19 0.0554 -0.013 0.0689 0.25 0.1 0.45 24 0.01 -0.0069 0.02 0.09 0.05 0.15 26 0.0425 -0.15 0.0638 0.185 0.124 0.32 Table Ⅹ Statistics of Trial Results for IQDE in 30-Bus System Containing DGS
No. Ploss Time No. Ploss Time No. Ploss Time 1 16.2163 24.2024 11 16.2163 29.7159 21 16.2164 28.0426 2 16.2163 25.9639 12 16.2163 29.4342 22 16.2163 23.9344 3 16.2164 34.057 13 16.2163 27.2983 23 16.2166 33.3986 4 16.2163 28.0157 14 16.2163 29.5571 24 16.2163 28.6112 5 16.2163 30.1713 15 16.2166 34.6243 25 16.2164 23.7194 6 16.2163 26.3804 16 16.2163 30.1448 26 16.2163 24.2563 7 16.2165 31.7187 17 16.2164 25.1229 27 16.2164 32.3472 8 16.2163 29.4458 18 16.2163 25.7156 28 16.2163 24.8397 9 16.2163 25.2483 19 16.2164 33.2381 29 16.2164 28.5767 10 16.2165 33.7229 20 16.2163 25.9665 30 16.2166 33.8194 Table Ⅺ Statistics of Trial Results (IEEE 30-Bus)
Results Average Min Max Ploss 16.2164 16.2163 16.2166 Time 28.7097 23.7194 34.6243 Table Ⅻ Statistics of Trial Results for IQDE in 30-Bus System Containing DGS
U1 U2 U5 U8 U11 U13 T11 T12 T15 T36 Q10 Q24 P1 1.06 1.045 1.01 1.01 1.082 1.071 1.06 1.04 0.96 1.04 10 3 P2 1.1 1.0759 1.0431 1.0462 1.1 1.1 0.9 1 1.02 0.9 20 4 -
[1] X. Y. Yin, X. Yan, X, Liu, and C. L. Wang, "Reactive power optimization based on improved hybrid genetic algorithm, " J. Northeast Dianli Univ. , vol. 34, no. 3, pp. 48-53, Jun. 2014. http://en.cnki.com.cn/Article_en/CJFDTOTAL-CGCZ201101020.htm [2] T. Y. Xiang, Q. S. Zhou, F. P. Li, and Y. Wang, "Research on niche genetic algorithm for Reactive Power Optimization, " Proc. CSEE, vol. 25, no. 17, pp. 48-51, Sep. 2005. http://en.cnki.com.cn/Article_en/CJFDTOTAL-ZGDC200517010.htm [3] M. Varadarajan and K. S. Swarup, "Network loss minimization with voltage security using differential evolution, " Electr. Power Syst. Res. , vol. 78, no. 5, pp. 815-823, May2008. http://www.researchgate.net/publication/223544555_Network_loss_minimization_with_voltage_security_using_differential_evolution [4] M. Basu, "Optimal power flow with FACTS devices using differential evolution, " Int. J. Electr. Power Energy Syst. , vol. 30, no. 2, pp. 150-156, Jan. 2008. https://www.researchgate.net/publication/222751245_Optimal_power_flow_with_FACTS_devices_using_differential_evolution [5] Y. T. Liu, L. Ma, and J. J. Zhang, "GA/SA/TS hybrid algorithms for reactive power optimization, " Proc. the IEEE Power Engineering Society Summer Meeting, Seattle, WA, USA, 2000, 245-249. https://www.researchgate.net/publication/3862451_GASATS_hybrid_algorithms_for_reactive_power_optimization [6] B. Zhao, C. X. Guo, and Y. J. Cao, "A multiagent-based particle swarm optimization approach for optimal reactive power dispatch, " IEEE Trans. on Power Syst. , vol. 20, no. 2, pp. 1070-1078, 2005. https://www.researchgate.net/publication/3267300_A_multiagent-based_particle_swarm_optimization_approach_for_optimal_reactive_power_dispatch [7] G. F. Fang, H. X. Wang, and X. S. Huang, "An improved genetic algorithm for reactive power optimization, " Proc. the EPSA, vol. 15, no. 4, pp. 15-18, Aug. 2003. http://en.cnki.com.cn/Article_en/CJFDTOTAL-DLZD200304004.htm [8] S. F. Wang, Z. P. Wan, H. Fan, C. Y. Xiang, and Y. G. Huang, "Reactive power optimization model and its hybrid algorithm based on bilevel programming, " Power Syst. Technol. , vol. 29, no. 9, pp. 22-25, May. 2005. https://www.researchgate.net/publication/290751059_Reactive_power_optimization_modeland_its_hybrid_algorithm_based_on_bilevel_programming [9] W. Liu, X. L. Liang, and X. L. An, "Power system reactive power optimization based on BEMPSO, " Power Syst. Protect. Control, vol. 38, no. 7, pp. 16-21, Apr. 2010. http://en.cnki.com.cn/Article_en/CJFDTOTAL-JDQW201007006.htm [10] L. F. Zheng, J. Y. Chen, H. Lin, S. L. Le, and F. Chen, "Reactive power optimization based on quantum particle swarm optimization in electrical power system, " Central China Electr. Power, vol. 24, no. 2, pp. 16-19, 2011. http://en.cnki.com.cn/Article_en/CJFDTOTAL-HZDL201102005.htm [11] B. Li, "Research of distribution reactive power optimization based on modified differential evolution algorithm, " M. S. thesis, North China Electr. Power Univ. , Beijing, China, 2012. [12] D. Devaraj and J. P. Roselyn, "Genetic algorithm based reactive power dispatch for voltage stability improvement, " Int. J. Electr. Power Energy Syst. , vol. 32, no. 10, pp. 1151-1156, Dec. 2010. https://www.researchgate.net/publication/229092065_Genetic_algorithm_based_reactive_power_dispatch_for_voltage_stability_improvement [13] Z. C. Hu, X. F. Wang, and G. Taylor, "Stochastic optimal reactive power dispatch: formulation and solution method, " Int. J. Electr. Power Energy Syst. , vol. 32, no. 6, pp. 615-62, Jul. 2010. https://www.researchgate.net/publication/245214843_Stochastic_optimal_reactive_power_dispatch_Formulation_and_solution_method [14] T. Malakar and S. K. Goswami, "Active and reactive dispatch with minimum control movements, " Int. J. Electr. Power Energy Syst, vol. 44, no. 1, pp. 78-87, Jan. 2013. https://www.researchgate.net/publication/256970308_Active_and_reactive_dispatch_with_minimum_control_movements [15] R. Storn and K. Price, "Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces, " J. Glob. Optim. , vol. 11, no. 4, pp. 341-359, Dec. 1997. [16] W. F. Gao, S. Y. Liu, and L. L. Huang, "A novel artificial bee colony algorithm based on modified search equation and orthogonal learning, " IEEE Trans. Cybernet. , vol. 43, no. 3, pp. 1011-1024, Jun. 2013. https://www.researchgate.net/publication/232533895_A_Novel_Artificial_Bee_Colony_Algorithm_Based_on_Modified_Search_Equation_and_Orthogonal_Learning [17] F. S. Abu-Mouti and M. E. El-Hawary, "Optimal distributed generation allocation and sizing in distribution systems via artificial bee colony algorithm, " IEEE Trans. Power Deliv. , vol. 26, no. 4, pp. 2090-2101, Oct. 2011. https://www.researchgate.net/publication/252062867_Optimal_Distributed_Generation_Allocation_and_Sizing_in_Distribution_Systems_via_Artificial_Bee_Colony_Algorithm [18] R. W. Keyes, "Quantum computing and digital computing, " IEEE Trans. Electron Devices, vol. 57, no. 8, pp. 2041, Aug. 2010. https://www.researchgate.net/publication/260512239_Quantum_Computing_and_Digital_Computing -





 下载:
下载:
 下载:
下载: