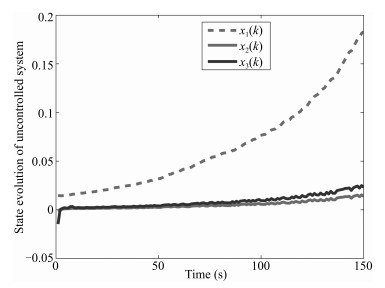
|
[1]
|
G. Feng, "A survey on analysis and design of model-based fuzzy control systems, "IEEE Trans. Fuzzy Syst. , vol. 14, no. 5, pp. 676-697, Oct. 2006.
|
|
[2]
|
C. C. Hua, Q. G. Wang, and X. P. Guan, "Adaptive fuzzy output-feedback controller design for nonlinear time-delay systems with unknown control direction, "IEEE Trans. Syst. Man Cybern. B Cybern. , vol. 39, no. 2, pp. 306-317, Apr. 2009. http://www.ncbi.nlm.nih.gov/pubmed/19095556
|
|
[3]
|
K. Tanaka, H. Ohtake, and H. O. Wang, "Guaranteed cost control of polynomial fuzzy systems via a sum of squares approach, "IEEE Trans. Syst. Man Cybern. B Cybern. , vol. 39, no. 2, pp. 561-567, Apr. 2009. http://europepmc.org/abstract/MED/19095549
|
|
[4]
|
L. G. Wu and W. X. Zheng, " L2/L∞ control of nonlinear fuzzy Itô stochastic delay systems via dynamic output feedback, "IEEE Trans. Syst. Man Cybern. B Cybern. , vol. 39, no. 5, pp. 1308-1315, Oct. 2009. http://ieeexplore.ieee.org/document/4804613/
|
|
[5]
|
H. L. Dong, Z. D. Wang, D. W. C. Ho, and H. J. Gao, "Robust H∞ fuzzy output-feedback control with multiple probabilistic delays and multiple missing measurements, "IEEE Trans. Fuzzy Syst. , vol. 18, no. 4, pp. 712-725, Aug. 2010. http://dl.acm.org/citation.cfm?id=1856597
|
|
[6]
|
J. B. Qiu, G. Feng, and H. J. Gao, "Fuzzy-model-based piecewise H∞ static-output-feedback controller design for networked nonlinear system, "IEEE Trans. Fuzzy Syst. , vol. 18, no. 5, pp. 919-934, Oct. 2010. http://dl.acm.org/citation.cfm?id=1892548
|
|
[7]
|
J. B. Qiu, G. Feng, and H. J. Gao, "Observer-based piecewise affine output feedback controller synthesis of continuous-time T-S fuzzy affine dynamic systems using quantized measurements, "IEEE Trans. Fuzzy Syst. , vol. 20, no. 6, pp. 1046-1062, Dec. 2012. http://dl.acm.org/citation.cfm?id=2721232
|
|
[8]
|
J. B. Qi, G. Feng, and H. J. Gao, "Static-output-feedback H∞ control of continuous-time T-S fuzzy affine systems via piecewise Lyapunov functions, "IEEE Trans. Fuzzy Syst. , vol. 21, no. 2, pp. 245-261, Apr. 2013. doi: 10.1109/tfuzz.2012.2210555
|
|
[9]
|
Y. Y. Cao and P. M. Frank, "Analysis and synthesis of nonlinear time-delay systems via fuzzy control approach, "IEEE Trans. Fuzzy Syst. , vol. 8, no. 2, pp. 200-211, Apr. 2000. http://dl.acm.org/citation.cfm?id=2234847
|
|
[10]
|
B. Chen, X. P. Liu, S. C. Tong, and C. Lin, "Observer-based stabilization of T-S fuzzy systems with input delay, "IEEE Trans. Fuzzy Syst. , vol. 16, no. 3, pp. 652-663, Jun. 2008. http://ieeexplore.ieee.org/document/4358823/
|
|
[11]
|
B. Chen and X. P. Liu, "Delay-dependent robust H∞ control for T-S fuzzy systems with time delay, "IEEE Trans. Fuzzy Syst. , vol. 13, no. 4, pp. 544-556, Aug. 2005. http://dl.acm.org/citation.cfm?id=2235274
|
|
[12]
|
H. J. Gao, Y. Zhao, and T. W. Chen, " H∞ fuzzy control of nonlinear systems under unreliable communication links, "IEEE Trans. Fuzzy Syst. , vol. 17, no. 2, pp. 265-278, Apr. 2009. http://ieeexplore.ieee.org/document/4505329/
|
|
[13]
|
X. F. Jiang and Q. L. Han, "On designing fuzzy controllers for a class of nonlinear networked control systems, "IEEE Trans. Fuzzy Syst. , vol. 16, no. 4, pp. 1050-1060, Aug. 2008. http://ieeexplore.ieee.org/document/4601110/
|
|
[14]
|
C. Lin, Q. G. Wang, T. H. Lee, and Y. He, "Design of observer-based H∞ control for fuzzy time-delay systems, "IEEE Trans. Fuzzy Syst. , vol. 16, no. 2, pp. 534-543, Apr. 2008. http://ieeexplore.ieee.org/document/4358786/
|
|
[15]
|
X. W. Liu, "Delay-dependent H∞ control for uncertain fuzzy systems with time-varying delays, "Nonlinear Anal. Theory Methods Appl. , vol. 68, no. 5, pp. 1352-1361, Mar. 2008. http://www.ams.org/mathscinet-getitem?mr=2381676
|
|
[16]
|
M. Liu, D. W. C. Ho, and Y. G. Niu, "Stabilization of markovian jump linear system over networks with random communication delay, "Automatica, vol. 45, no. 2, pp. 416-421, Feb. 2009. http://dl.acm.org/citation.cfm?id=1497637.1497905
|
|
[17]
|
S. K. Nguang and P. Shi, "Fuzzy H∞ output feedback control of nonlinear systems under sampled measurements, "Automatica, vol. 45, no. 12, pp. 2169-2174, Dec. 2003. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=980889
|
|
[18]
|
S. K. Nguang and P. Shi, "H∞ fuzzy output feedback control design for nonlinear systems: An LMI approach, "IEEE Trans. Fuzzy Syst. , vol. 11, no. 3, pp. 331-340, Jun. 2003. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1203792
|
|
[19]
|
M. Sahebsara, T. W. Chen, and S. L. Shah, "Optimal H∞ filtering in networked control systems with multiple packet dropouts, "Syst. Control Lett. , vol. 57, no. 9, pp. 696-702, Sep. 2008. doi: 10.1016/j.sysconle.2008.01.011
|
|
[20]
|
P. Seiler and R. Sengupta, "An H∞ approach to networked control, "IEEE Trans. Automat. Control, vol. 50, no. 3, pp. 356-364, Mar. 2005. http://www.ams.org/mathscinet-getitem?mr=2123096
|
|
[21]
|
S. L. Sun, L. H. Xie, and W. D. Xiao, "Optimal full-order and reduced-order estimators for discrete-time systems with multiple packet dropouts, "IEEE Trans. Signal Process. , vol. 56, no. 8, pp. 4031-4038, Aug. 2008. http://dl.acm.org/citation.cfm?id=2197942.2201355&coll=DL&dl=GUIDE&CFID=431149417&CFTOKEN=23120143
|
|
[22]
|
Z. D. Wang, D. W. C. Ho, Y. R. Liu, and X. H. Liu, "Robust H∞ control for a class of nonlinear discrete time-delay stochastic systems with missing measurements, "Automatica, vol. 45, no. 3, pp. 684-691, Mar. 2009. http://dl.acm.org/citation.cfm?id=1513258
|
|
[23]
|
H. N. Wu, "Delay-dependent H∞ fuzzy observer-based control for discrete-time nonlinear systems with state delay, "Fuzzy Sets Syst. , vol. 159, no. 20, pp. 2696-2712, Oct. 2008. http://dl.acm.org/citation.cfm?id=1403334
|
|
[24]
|
H. N. Wu and K. Y. Cai, " H2 guaranteed cost fuzzy control for uncertain nonlinear systems via linear matrix inequalities, "Fuzzy Sets Syst. , vol. 148, no. 3, pp. 411-429, Dec. 2004. http://www.ams.org/mathscinet-getitem?mr=2101200
|
|
[25]
|
F. W. Yang, Z. D. Wang, Y. S. Hung, and M. Gani, "H∞ control for networked systems with random communication delays, "IEEE Trans. Automat. Control, vol. 51, no. 3, pp. 511-518, Mar. 2006. http://ieeexplore.ieee.org/document/1605414/
|
|
[26]
|
D. Yue, E. G. Tian, Y. J. Zhang, and C. Peng, "Delay-distribution-dependent stability and stabilization of T-S fuzzy systems with probabilistic interval delay, "IEEE Trans. Syst. Man Cybern. Part B, Cybern. , vol. 39, no. 2, pp. 503-516, Apr. 2009.
|
|
[27]
|
H. G. Zhang, M. Li, J. Yang, and D. D. Yang, "Fuzzy model-based robust networked control for a class of nonlinear systems, "IEEE Trans. Syst. Man Cybern. Part A, Syst. Hum. , vol. 39, no. 2, pp. 437-447, Mar. 2009. http://ieeexplore.ieee.org/document/4757263/
|
|
[28]
|
L. Q. Zhang, Y. Shi, T. W. Chen, and B. Huang, "A new method for stabilization of networked control systems with random delays, "IEEE Trans. Automat. Control, vol. 50, no. 8, pp. 1177-1181, Aug. 2005. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=1470028
|
|
[29]
|
Y. Zhao, J. Wu, and P. Shi, "H∞ control of non-linear dynamic systems: A new fuzzy delay partitioning approach, "IET Control Theory Appl. , vol. 3, no. 7, pp. 917-928, Jul. 2009. http://www.ams.org/mathscinet-getitem?mr=2537969
|
|
[30]
|
M. X. Liu, X. T. Liu, Y. Shi, and S. Q. Wang, "T-S fuzzy-model-based H2 and H∞ filtering for networked control systems with two-channel Markovian random delays, "Dig. Signal Process. , vol. 27, pp. 167-174, Apr. 2014. http://dl.acm.org/citation.cfm?id=2608860.2609119
|
|
[31]
|
L. Qiu, Y. Shi, F. Q. Yao, G. Xu, and B. G. Xu, "Network-based robust H2/ H∞ control for linear systems with two-channel random packet dropouts and time delays, "IEEE Trans. Cyber. , vol. 45, no. 8, pp. 1450-1462, Aug. 2015. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6897996
|
|
[32]
|
L. X. Zhang, "H∞ estimation for discrete-time piecewise homogeneous Markov jump linear systems, "Automatica, vol. 45, no. 11, pp. 2570-2576, Nov. 2009. http://www.ams.org/mathscinet-getitem?mr=2889314
|
|
[33]
|
L. X. Zhang, N. G. Cui, M. Liu, and Y. Zhao, "Asynchronous filtering of discrete-time switched linear systems with average dwell time, "IEEE Trans. Circ. Syst. Ⅰ Regul. Pap., vol. 58, no.5, pp.1109-1118, May2011. doi: 10.1109/TCSI.2010.2092151
|
|
[34]
|
W. Assawinchaichote, S. K. Nguang, P. Shi, and E. Boukas, "H∞ fuzzy state-feedback control design for nonlinear systems with D-stability constraints: An LMI approach, "Math. Comput. Simul. , vol. 78, no. 4, pp. 514-531, Aug. 2008. http://www.ams.org/mathscinet-getitem?mr=2424560
|
|
[35]
|
X. P. Guan and C. L. Chen, "Delay-dependent guaranteed cost control for T-S fuzzy systems with time delays, "IEEE Trans. Fuzzy Syst. , vol. 12, no. 2, pp. 236-249, Apr. 2004. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1284326
|
|
[36]
|
L. El Ghaoui, F. Oustry, and M. A. Rami, "A cone complementarity linearization algorithm for static output-feedback and related problems, "IEEE Trans. Automat. Control, vol. 42, no. 8, pp. 1171-1176, Aug. 1997. http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=618250
|
|
[37]
|
H. J. Gao, Z. D. Wang, and C. H. Wang, "Improved H∞ control of discrete-time fuzzy systems: A cone complementarity linearization approach, "Inf. Sci. , vol. 175, no. 1-2, pp. 57-77, Sep. 2005. http://www.sciencedirect.com/science/article/pii/S0020025504002932
|




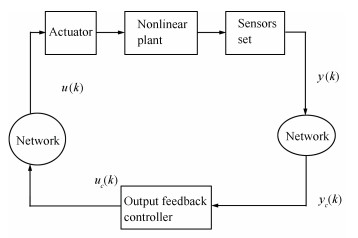
 下载:
下载: