-
摘要: 针对常用混合动力汽车（Hybrid electric vehicle，HEV）中锂离子电池在功率波动较大时难以满足需求，以及单个驱动周期内HEV燃油能耗大且能量不能很好回收等问题，研究采用锂离子电池和超级电容器混合储能系统（Lithium-ion battery and super-capacitor hybrid energy storage system，Li-SC HESS）与内燃机共同驱动HEV运行.结合比例积分粒子群优化算法（Particle swarm optimization-proportion integration，PSO-PI）控制器和Li-SC HESS内部功率限制管理办法，提出一种改进的基于庞特里亚金极小值原理（Pontryagin's minimum principle，PMP）算法的HEV能量优化控制策略，通过ADVISOR软件建立HEV整车仿真模型，验证该方法的有效性与可行性.仿真结果表明，该能量优化控制策略提高了HEV跟踪整车燃油能耗最小轨迹的实时性，节能减排比改进前提高了1.6%~2%，功率波动时减少了锂离子电池的出力，进而改善了混合储能系统性能，对电动汽车关键技术的后续研究意义重大.
-
关键词:
- 混合动力汽车 /
- 混合储能系统 /
- PSO-PI控制 /
- 庞特里亚金极小值原理
Abstract: Common hybrid electric vehicles (HEVs) usually suffer lithium-ion battery power fluctuations and it is difficult for them to meet the demand. This also constraints the performance of the energy storage system in which there is a the large amount of fuel consumption with less energy recovery of HEV in a single drive cycle. This paper selects a lithium-ion battery and super-capacitor hybrid energy storage system (Li-SC HESS) to drive the hybrid electric vehicle running together with an internal combustion engine. Besides, combined with particle swarm optimization-proportion integration (PSO-PI) controller and Li-SC HESS internal power limit management approach, this paper presents an improved HEV energy optimization control strategy based on the Pontryagin's minimum principle (PMP) algorithm. A simulation model of HEV is established by ADVISOR software to verify the effectiveness and feasibility of the strategy. Results show that the energy optimization control strategy can improve the real-time ability of tracking the smallest track of HEV fuel consumption function for the purpose of energy conservation. The energy-saving emission reduction ratio is improved by 1.6% to 2.0%. Moreover, when power fluctuates the output of lithium-ion battery is reduced, thus improving the performance of the Li-SC HESS. The research is significant to the follow-up study on the key technologies in electric vehicles. -
DC-DC变换器是指能完成直流电路电压转换的电力电子装置, 目前主要应用于直流电压转换、开关电源、直流电机驱动等场合.从功能上来区分, DC-DC变换器可以分为Buck变换器 (降压)、Boost变换器 (升压)、Boost-Buck变换器 (升--降压) 和Buck-Boost变换器 (降--升压) [1].随着现代工业技术的发展, 对直流变换器的要求越来越高, 既要求系统轻便、稳定、可靠, 又要求系统有较高的动态性能.由于DC-DC变换器是一类典型的开关非线性系统, 传统的线性控制设计方法很难保证系统较高的性能.因此, 结合DC-DC变换器模型特点, 研究先进的非线性控制方法已成为电力电子变换器系统研究的一个重要内容.本文主要针对Buck变换器, 提出一种新的非线性控制方法, 以实现电压的快速调节.
目前, 已有不少文献展开对Buck变换器的非线性控制方法研究.文献[2 $-$ 5]分别利用反步法、自适应控制、滑模控制、模糊控制对DC-DC变换器系统设计非线性控制算法, 以提高闭环系统的性能.文献[6]提出通过构造Lyapunov函数来分析和设计一类电力电子变换器的非线性控制系统.文献[7]利用非线性函数设计非线性PI控制器, 比传统线性PI有更好的调节效果和控制性能.文献[8]利用非线性采样输出反馈理论, 设计了一类针对Buck变换器的非线性控制算法, 以提高系统的鲁棒性.文献[9]利用扩展状态观测器, 设计了一类针对Buck变换器的非线性滑模控制算法, 提高了系统抗负载突变的能力.
值得指出的是, 前述所提及的非线性控制算法基本上都要求闭环系统满足局部利普希兹条件, 从而只能保证闭环系统的渐近稳定性[10].从收敛性角度来说, 在实际应用中, 更希望电压能在有限时间内收敛到参考电压.近年来, 有限时间控制算法作为一种新发展的非线性控制算法, 它可以保证闭环系统状态在有限时间内收敛到平衡点.目前, 这种控制方法在理论界[11-16]和应用界[17-23]已得到了广泛的关注.此外, 对于Buck变换器而言, 由于其外部负载常随时间而变化, 如何提高闭环系统抗负载变化能力也是控制算法设计关注的焦点问题之一.当系统存在干扰时, 有限时间控制算法还具有较强的抗负载变化能力, 具体见文献[24]中的理论分析以及文献[17]中的实验验证.文献[25]基于终端滑模控制技术, 对Buck变换器系统设计了有限时间控制器, 但该文献并没有考虑输入饱和受限和负载未知情况.
本文主要针对Buck变换器系统模型特点, 基于有限时间控制理论, 设计了一类有界的非线性自适应控制算法, 以实现电压的快速调节, 并同时满足系统对占空比函数有界约束的要求.首先, 基于时间尺度变换, 引入一个可调的参数, 得到变换后的系统; 然后, 通过构造合适的Lyapunov函数, 设计一类饱和的有限时间控制器; 最后, 利用齐次性理论, 得出系统是有限时间稳定的结论, 即输出电压在有限时间内收敛到参考电压.对负载未知情况, 基于有限时间观测器理论, 设计了自适应控制方法, 以实现对未知负载的估计.本文最后给出仿真实验结果, 并与PI控制算法进行了性能对比.仿真结果表明, 所提出的控制算法使得系统既具有较快的响应速度又有较强的抗负载变化能力.
1. 模型介绍及预备知识
1.1 Buck型DC-DC变换器系统模型
Buck型DC-DC变换器工作原理如图 1所示, 其中 $V_{\rm in}$ 是输入电压, $V_o$ 是输出电压, $S$ 是MOS型开关, $D$ 是二极管, $L$ 、 $C$ 、 $R$ 分别是电感、电容和负载电阻, $i_L$ 是电感电流.在开关频率足够快的情况下, DC-DC变换器可以近似为一般的状态空间模型, 其状态方程为[4]:
$ \begin{align}\label{zhtfc} &\dot i_L=\frac{1}{L} (\mu V_{\rm in}-V_o)\notag\\ &\dot V_o=\frac{1}{C} \left(i_L-\frac{V_o}{R}\right) \end{align} $
(1) 其中, $\mu$ 是控制输入, 即为MOS型开关管 $S$ 的占空比, $\mu \in [0, 1]$ .
假设 $V_{\rm ref}$ 为期望参考输出电压.令 $x_1=V_{\rm ref}-V_o$ 为输出电压误差, 则可以得到误差动态方程为
$ \begin{align}\label{wcdtfc} &\dot x_1=x_2=-\frac{{\rm d}V_o}{{\rm d}t}\notag\\ &\dot x_2=-\frac{1}{LC}x_1-\frac{1}{RC}x_2-\frac{V_{\rm in}}{LC}\mu +\frac{V_{\rm ref}}{LC}\notag\\ &y=x_1 \end{align} $
(2) 1.2 时间尺度坐标变换
为便于控制器设计, 对方程 (2) 进行时间尺度的坐标变换.令 $t=Ms$ , 其中 $M$ 为待设计的一个正常数.定义坐标变换:
$ \begin{align}\label{zbbh} &z_1(s)=x_1(Ms)=x_1(t)\notag \\ &z_2(s)=Mx_2(Ms)=Mx_2(t)\notag \\ &u(s)=M^2\mu(Ms)=M^2\mu(t) \end{align} $
(3) 那么根据式 (2) 可得:
$ \begin{align}\label{bianxing} &\frac{{\rm d}z_1(s)}{{\rm d}s}=\frac{{\rm d}x_1(Ms)}{{\rm d}s}=Mx_2(Ms)=z_2(s)\notag \\ &\quad\frac{{\rm d}z_2(s)}{{\rm d}s}=M\frac{{\rm d}x_2(Ms)}{{\rm d}s}=\notag\\ &\quad -\frac{1}{LC}M^2z_1(s)-\frac{1}{RC}Mz_2(s)-\notag\\ &\quad \frac{V_{\rm in}}{LC}u(s)+\frac{V_{\rm ref}}{LC}M^2 \end{align} $
(4) 为了便于设计控制器, 令
$ \begin{align}\label{canshutihuan} &b_1=\frac{1}{LC}M^2\notag \\ &b_2=\frac{1}{RC}M\notag \\ &f(s)=-\frac{V_{\rm in}}{LC}u(s)+\frac{V_{\rm ref}}{LC}M^2 \end{align} $
(5) 则方程 (2) 可简化为
$ \begin{align}\label{huajianmoxing} &\frac{{\rm d}z_1(s)}{{\rm d}s}=z_2(s)\notag \\ &\frac{{\rm d}z_2(s)}{{\rm d}s}=-b_1z_1(s)-b_2z_2(s)+f(s) \end{align} $
(6) 其中, $b_1>0, b_2>0$ , $f(s)$ 是控制器.
1.3 相关定义和引理
定义1.为了书写方便, 记
$ \begin{align}\label{sig} sig^\alpha(x)={\rm sgn}(x) |x|^\alpha \end{align} $
(7) 其中, $\alpha\geq0$ , $x\in \boldsymbol{R}$ , ${\rm sgn}(\cdot)$ 为符号函数.
定义2.定义一类新的饱和函数
$ \begin{align} sat_{\alpha}(x)=\left\{ {\begin{array}{*{20}c} { {\rm sgn}(x), |x|>1} \\ sig^\alpha(x), |x|\leq1 \end{array}} \right. \end{align} $
(8) 其中, $0\leq\alpha\leq1$ , $x\in \boldsymbol{R}$ .
定义3[4].令 $f(x)=(f_1(x), \cdots, f_n(x))^{\rm T}:{{\mathbf{R}}^{n}}\rightarrow {\bf R}^n$ 为一向量函数.若对任意的 $\varepsilon>0$ , 存在 $(r_1, \cdots, r_n)$ , 其中 $r_i>0, i=1, \cdots, n, $ 使得 $f(x)$ 满足:
$ f_i(\varepsilon^{r_1}x_1, \cdots, \varepsilon^{r_n}x_n)=\varepsilon^{k+r_i}f_i(x), \quad i=1, \cdots, n $
其中, $k>-{\rm min}\{r_i, i=1, \cdots, n\}$ , 则称 $f(s)$ 关于 $(r_1, \cdots, r_n)$ 具有齐次度 $k$ , 其中 $(r_1, \cdots, r_n)$ 称为扩张.
定义4[24].考虑系统
$ \begin{align} \dot x=f(x), x \in U \subseteq {{\mathbf{R}}^{n}}, f(0)=0 \end{align} $
(9) 其中, $f:U\rightarrow \boldsymbol{R}^n$ 为开区域 $U$ 上对 $x$ 连续的函数, 且开区域 $U$ 包含原点.系统的解 $x=0$ 为有限时间稳定当且仅当系统是稳定的且为有限时间收敛的.所谓有限时间收敛指的是:对 $\forall x_0\in U_0\subset {\bf R}^n$ , 存在一个连续函数 $T(x):U_0\setminus\{0\}\rightarrow(0, +\infty)$ , 使得系统 (9) 的解 $x(t, x_0)$ 满足:当 $t\in [0, T(x_0))$ 时, 有 $x(t, x_0)\in U_0\setminus{\{0\}}$ 和 $\lim\nolimits_{x\to T(x_0)}x(t, x_0)=0$ ; 当 $t>T(x_0)$ 时, 有 $x(t, x_0)=0$ .若 $U=U_0={\bf R}^n$ , 则系统是全局有限时间稳定的.
引理1[26].对于如下系统
$ \begin{align} \dot x=f(x)+\hat f(x), \quad x\in {{\mathbf{R}}^{n}} \end{align} $
(10) 其中, $f(x)$ 是连续的齐次向量空间, 且针对扩张 $(r_1, \cdots, r_n)$ 具有齐次度 $k < 0$ , 函数 $\hat f(x)$ 满足 $\hat f(0)=0$ .如果 $x=0$ 是系统 $\dot x=f(x)$ 的渐近稳定平衡点, 且对 $\forall x\neq0$ ,
$ \begin{align} \frac{\hat f_i(\varepsilon^{r_1}x_1, \cdots, \varepsilon^{r_n}x_{n})}{\varepsilon^{r_i+k}}=0, \quad i=1, 2, \cdots, n \end{align} $
(11) 那么 $x=0$ 是系统 (10) 的一个局部有限时间平衡点.如果系统 (10) 既是全局渐近稳定的, 又是局部有限时间稳定的, 那么它是全局有限时间稳定的.
2. 饱和有限时间控制器设计
在本节中, 主要针对坐标变换后的系统 (6) 进行饱和有限时间控制器设计.简便起见, 本节中省略的变量求导都是针对变量 $s$ .
定理1.对于系统 (6), 如果控制器设计成
$ \begin{align} f=-k_1sat_{\alpha_1}(z_1)-k_2sat_{\alpha_2}(z_2) \end{align} $
(12) 其中, $k_1 > 0, k_2 > 0, 0 < \alpha_1 < 1, \alpha_2=2\alpha_1/(1+\alpha_1)$ , 那么系统 (6) 的状态可以在有限时间被镇定到原点, 即在有限时间内, $(z_1(s), z_2(s))=0$ .
证明.证明可分为两个步骤.
步骤1. {证明全局渐近稳定性}
取Lyapunov函数:
$ \begin{align} V=k_1\int_0^{z_1}sat_{\alpha_1}(\rho){\rm d}\rho+\frac{1}{2}b_1z_1^2+\frac{1}{2}z_2^2 \end{align} $
(13) 由于 $\frac{{\rm d}\int_0^{z_1}sat_{\alpha_1}(\rho){\rm d}\rho}{{\rm d}s}=sat_{\alpha_1}(z_1)\dot z_1$ , 那么
$ \begin{align} &\dot V|_{(6)}=k_1sat_{\alpha_1}(z_1)z_2+b_1z_1z_2-b_1z_1z_2-b_2z_2^2+z_2f=\notag\\ &\quad k_1sat_{\alpha_1}(z_1)z_2-b_2z_2^2+z_2f \end{align} $
(14) 在所设计的控制器 (12) 作用下, 可得:
$ \begin{align} &\dot V|_{(6)-(12)}=k_1sat_{\alpha_1}(z_1)z_2-b_2z_2^2-\notag\\ &\quad k_1z_2sat_{\alpha_1}(z_1)-k_2z_2sat_{\alpha_2}(z_2)=\notag\\ &\quad -b_2z_2^2-k_2z_2sat_{\alpha_2}(z_2) \end{align} $
(15) 当 $|z_2|>1$ 时, $z_2sat_{\alpha_2}(z_2)=|z_2|$ , 当 $|z_2|\leq1$ 时, $z_2sat_{\alpha_2}(z_2)=|z_2|^{\alpha_2+1}$ , 故 $\dot V\leq0$ .
记集合 $\Psi=\{(z_1, z_2)|\dot V\equiv0\}$ .由式 (15) 可知 $\dot V\equiv0$ 意味着 $z_2\equiv0$ .亦即 $\dot z_2\equiv0$ .进一步根据式 (6) 和式 (12), 可以得到 $-b_1z_1-k_1sat_{\alpha_1}(z_1)\equiv0$ .注意到 $b_1, k_1$ 为正的增益, 从而 $z_1\equiv0$ .因此, 根据LaSalle不变集原理[27], 可以得出, 当 $s\to0$ 时, $(z_1(s), z_2(s))\to0$ , 即系统 (6) 在控制器 (12) 作用下是渐近稳定的.
步骤2.证明局部有限时间稳定
将闭环系统 (6) 和 (12) 重新写成如下形式:
$ \begin{align} &\dot z_1=z_2\notag\\ &\dot z_2=-k_1sat_{\alpha_1}(z_1)-k_2sat_{\alpha_2}(z_2)+g(z_1, z_2) \end{align} $
(16) 其中, $g(z_1, z_2)=-b_1z_1-b_2z_2$ .
由步骤1证明可知, 系统 (16) 是全局渐近稳定的, 那么系统的状态 $(z_1, z_2)$ 在有限时间内进入区域 $|z_1|\leq1, |z_2|\leq1$ .由饱和函数定义2, 此时系统 (16) 退化成为如下形式:
$ \begin{align} &\dot z_1=z_2\notag\\ &\dot z_2=-k_1sig^{\alpha_1}(z_1)-k_2sig^{\alpha_2}(z_2)+g(z_1, z_2) \end{align} $
(17) 对于系统 (17) 的标称系统:
$ \begin{align} \dot z_1&=z_2\notag\\ \dot z_2&=-k_1sig^{\alpha_1}(z_1)-k_2sig^{\alpha_2}(z_2) \end{align} $
(18) 构造Lyapunov函数如下:
$ \begin{align} W=k_1\int_0^{z_1}sig^{\alpha_1}(\rho) {\rm d}\rho+\frac {1}{2}z_2^2 \end{align} $
(19) 沿着系统 (18), 对式 (19) 进行求导, 得:
$ \begin{align} \dot W|_{(18)}=-k_2z_2sig^{\alpha_2}(z_2)=-k_2|z_2|^{\alpha_2+1} \end{align} $
(20) 故 $\dot W\leq0$ .
通过和步骤1类似的证明, 可以证明对于系统 (18), 当 $s\to\infty$ 时, 有 $(z_1(s), z_2(s))\to0$ , 亦即系统 (18) 是渐近稳定的.
另外由于 $0 < \alpha_1 < 1, \alpha_2=2\alpha_1/(1+\alpha_1)$ , 根据齐次性定义 (即定义3), 可知系统 (18) 的齐次度为 $m=(\alpha_1-1)/2 < 0$ , 其中 $r_1=1, r_2=(\alpha_1+1)/2$ .
接下来证明对于 $\forall(z_1, z_2)\neq(0, 0)$ , 有:
$ \lim\limits_{\varepsilon\to0}\frac{g(\varepsilon^{r_1}z_1, \varepsilon^{r_2}z_2)}{\varepsilon^{r_2+m}}=0 $
根据函数 $g(\cdot)$ 的定义, 有:
$ \begin{align} &\lim\limits_{\varepsilon\to0}\frac{g(\varepsilon^{r_1}z_1, \varepsilon^{r_2}z_2)}{\varepsilon^{r_2+m}}= \lim\limits_{\varepsilon\to0}\frac{-b_1\varepsilon^{r_1}z_1-b_2\varepsilon^{r_2}z_2}{\varepsilon^{r_2+m}}=\notag\\ &\quad \lim\limits_{\varepsilon\to0}(-b_1\varepsilon^{r_1-r_2-m}z_1-b_2\varepsilon^{-m}z_2)\notag \end{align} $
因为 $r_1 > r_2, m < 0$ , 所以 $\lim\nolimits_{\varepsilon\to0}(-b_1\varepsilon^{r_1-r_2-m}z_1-b_2\varepsilon^{-m}z_2)=0$ , 即 $\lim\nolimits_{\varepsilon\to0}\frac{g(\varepsilon^{r_1}z_1, \varepsilon^{r_2}z_2)}{\varepsilon^{r_2+m}}=0$ .因此, 根据引理1可知, 系统 (17) 是全局有限时间稳定的, 亦即系统 (16) 是局部有限时间稳定的.综合步骤1和步骤2, 可以得出系统 (6) 在控制器 (12) 的作用下是全局有限时间稳定.
注1.很显然, 所设计的控制器 (12) 是有界的.根据饱和函数的定义2, 可知 $|f|\leq k_1+k_2$ .因此, 为了满足实际系统对控制器饱和约束的条件, 可以调节控制参数 $k_1, k_2$ 满足任何约束条件.
3. Buck变换器快速有限时间降压控制算法设计
定理2.对于Buck型变换器系统 (1), 如果占空比函数设计成
$ \begin{align} \mu(t)=\frac{V_{\rm ref}}{V_{\rm in}}+\frac{LC}{M^2V_{\rm in}}[k_1sat_{\alpha_1}(x_1(t))+k_2sat_{\alpha_2}(M\cdot x_2(t))] \end{align} $
(21) 其中, $k_1 > 0, k_2 > 0, 0 < \alpha_1 < 1, \alpha_2=2\alpha_1/(1+\alpha_1)$ , 那么系统的输出电压 $V_o$ 可以在有限时间内达到参考电压 $V_{\rm ref}$ .
证明.首先, 对于所设计的控制器 (21), 在时间尺度 $t=Ms$ 变换下有:
$ \begin{align} &\mu(Ms)=\frac{V_{\rm ref}}{V_{\rm in}}+\frac{LC}{M^2V_{\rm in}}[k_1sat_{\alpha_1}(x_1(Ms))+\notag\\ &\quad k_2sat_{\alpha_2}(M\cdot x_2(Ms))] \end{align} $
(22) 在式 (22) 两边同时乘以 $M^2$ , 有:
$ \begin{align} &M^2\cdot\mu(Ms)=\frac{V_{\rm ref}}{V_{\rm in}}M^2+\frac{LC}{V_{\rm in}}[k_1sat_{\alpha_1}(x_1(Ms))+\notag\\ &\quad k_2sat_{\alpha_2}(M\cdot x_2(Ms))] \end{align} $
(23) 基于坐标变换 (3), 可得:
$ \begin{align} u(s)=\frac{V_{\rm ref}}{V_{\rm in}}M^2+\frac{LC}{V_{\rm in}}[k_1sat_{\alpha_1}(z_1(s))+k_2sat_{\alpha_2}(z_2(s))] \end{align} $
(24) 进一步, 根据式 (5) 可得:
$ \begin{align} &f(s)=-\frac{V_{\rm in}}{LC}u(s)+\frac{V_{\rm ref}}{LC}M^2=\notag\\ &\quad -k_1sat_{\alpha_1}(z_1(s))-k_2sat_{\alpha_2}(z_2(s)) \end{align} $
(25) 因此, 基于定理1, 可证明系统 (1) 在控制器 (21) 作用下是全局有限时间稳定的, 即输出电压 $V_o$ 能在有限时间内稳定到参考电压 $V_{\rm ref}$ .
注2.对于所设计的占空比函数 (21), 其大小满足:
$ \begin{align} \frac{V_{\rm ref}}{V_{\rm in}}-\frac{LC}{M^2V_{\rm in}}(k_1+k_2)\leq\mu\leq\frac{V_{\rm ref}}{V_{\rm in}}+\frac{LC}{M^2V_{\rm in}}(k_1+k_2) \end{align} $
(26) 由于 $0 < V_{\rm ref}/V_{\rm in} < 1$ , 因此很方便调节参数 $M, k_1, k_2$ 保证 $0 < \mu < 1$ .
4. Buck变换器快速自适应有限时间降压控制算法设计
本节中, 将考虑负载电阻突变情况下的有限时间降压控制算法设计问题.根据式 (1) 和 (2) 可知, 为了获得状态 $x_2$ , 需要精确知道负载 $R$ .然而实际中负载往往是随时间而变化的.接下来将主要基于有限时间观测器技术对未知负载在有限时间内估计其精确值.
令 $\hat R$ 为未知负载 $R$ 的估计值.为了便于设计, 令 $\theta=-1/R$ 为未知的参数, 令 $\hat\theta$ 为其估计值.
定理3.对于Buck变换器的未知负载电阻, 如果估计器设计为
$ \begin{align} &\dot{\hat{V}}_o=\frac{1}{C}(i_L+\hat\theta V_o)+l_1V_osig^{\beta_1}(V_o-\hat{V}_o)\notag\\ &\dot{\hat{\theta}}=l_2V_osig^{\beta_2}(V_o-\hat{V}_o) \end{align} $
(27) 那么估计值 $\hat\theta$ (或 $\hat R=-1/\hat\theta$ ) 在有限时间内收敛到真实值 $\theta$ (或 $R$ ), 其中 $l_1, l_2$ 为合适的正增益, $0.5 < \beta_1 < 1, \beta_2=2\beta_1-1$ .
证明.定义估计器误差
$ \begin{align} e_1=V_o-\hat{V}_o, e_2=\theta-\hat\theta \end{align} $
(28) 注意到 $\theta$ 是一个常数, 那么根据式 (27) 和 (28) 可得:
$ \begin{align} &\dot{\hat{e}}_1=\frac{V_o}{C}e_2-l_1V_osig^{\beta_1}(e_1)\notag\\ &\dot{\hat{e}}_2=-l_2V_osig^{\beta_2}(e_1) \end{align} $
(29) 基于文献[28]中的定理3.1, 可知存在合适的增益使得该系统是有限时间收敛的, 即估计值 $\hat\theta$ 在有限时间内收敛到真实值 $\theta$ , 亦即负载估计值 $\hat R=-1/\hat \theta$ 在有限时间内收敛到真实负载 $R$ .
基于定理3, 针对Buck变换器负载未知情况, 根据式 (1)、(2) 和式 (21), 可以设计自适应有限时间控制算法的形式如下:
$ \begin{align} &\mu (t)=\frac{V_{\rm ref}}{V_{\rm in}}+\frac{LC}{M^2V_{\rm in}} [k_1sat_{\alpha_1}(x_1(t))+k_2sat_{\alpha_2}(M\hat x_2)]=\notag\\ &\quad \frac{V_{\rm ref}}{V_{\rm in}}+\frac{LC}{M^2V_{\rm in}}[k_1sat_{\alpha_1}(V_{\rm ref}-V_o)+\notag\\ &\quad k_2sat_{\alpha_2}\left[\frac {M}{C}\left(\frac{V_o}{\hat R}-i_L\right)\right] \end{align} $
(30) 图 2给出了自适应有限时间电压调节控制算法框图.
图 2 自适应有限时间电压调节控制算法实现框图Fig. 2 The block diagram of adaptive finite-time voltage control algorithm5. 仿真实验
本实验采用针对电力电子及电机拖动开发的专用仿真软件PSIM (Power simulation) 软件进行仿真, 控制策略图见图 2, 其中三角波的频率选择100 kHz.
5.1 系统仿真参数
在仿真中Buck变换器的参数选取为:输入电压 $V_{\rm in}=12$ V, 电感值 $L=5$ mH, 电容值 $C=1 000 \mu$ F, 负载电阻值 $R=30 \Omega$ , 输出参考电压 $V_{\rm ref}=8$ V.为了进行对比, 采用自适应有限时间控制 (Automatic frequency control, AFC) 与PI (Proportional integral control) 控制两种算法.
对于自适应有限时间控制算法式 (30) 和 (27), 参数值分别选为: $M=0.001$ , $k_1=0.225$ , $k_2=1, \alpha_1=1/5$ , $l_1=160$ , $l_2=6, \beta_1=0.55$ .
对于PI控制算法, 其比例和积分增益分别为 $K_P=0.1$ , $K_I=0.05$ .
分别考虑在启动过程、参考电压变化以及负载突变情况下系统动态响应性能.
5.2 参考电压变化情况下动态响应
负载保持30 $\Omega$ 不变, 参考电压在1 s时从8 V变化到5 V, 其他参数保持不变.系统动态响应波形见图 3.可以明显看出, 所提出的快速有限时间电压控制算法对参考电压变化的响应速度明显优于PI控制, 其中AFC控制的系统在开始启动时的调节时间是0.007 s, 1 s时参考电压变化时的调节时间是0.06 s; PI控制系统在开始启动时的调节时间是0.32 s, 1 s时参考电压变化时的调节时间是0.24 s.
图 3 两种控制算法作用下输出电压响应曲线 (1 s时, 参考电压由8 V $\to$ 5 V)Fig. 3 The response curves for output voltage under two control algorithms (At 1 second, reference voltage is from 8 V $\to$ 5 V.)5.3 负载突变情况下动态响应
负载电阻变化如下:
$ \begin{align} {R}=\left\{ {\begin{array}{*{20}c} { {30}, 0\leq t\leq0.5 {\rm s}} \\ { {15}, 0.5 {\rm s} < t\leq1 {\rm s}} \\ { {30}, t > 1 {\rm s}} \\ \end{array}} \right. \end{align} $
(31) 其他参数保持不变.可以得到系统响应如图 4.负载电阻估计值响应曲线如图 5.
图 4 两种控制算法作用下输出电压响应曲线 (0.5 s时, 负载电阻由30 $\Omega\to15 \Omega$ ; 1 s时, 负载电阻由15 $\Omega\to30 \Omega$ )Fig. 4 The response curves for output voltage under two control algorithms (At 0.5 second, load resistance is from 30 $\Omega\to15 \Omega$ ; at 1 second, load resistance is from 15 $\Omega\to30 \Omega$ .AFC控制的系统在负载由30 $\Omega\to 15 \Omega$ 的调节时间为0.018 s, 电压波动范围为7.964 V $\sim$ 8 V, 在负载由15 $\Omega\to 30 \Omega$ 的调节时间为0.013 s, 电压波动范围为8 V $\sim$ 8.054 V。
PI控制的系统在负载由30 $\Omega\to 15 \Omega$ 的调节时间为0.034 s, 电压波动范围为7.631 V $\sim$ 8.365 V, 在负载由15 $\Omega\to 30 \Omega$ 的调节时间为0.048 s, 电压波动范围为7.628 V $\sim$ 8.368 V.
可见, 所提出的快速自适应有限时间降压控制方法对负载突变的响应更快, 电压波动更小.
上述结果表明, 相对于PI控制, 所提出的快速自适应有限时间降压控制算法具有较快的收敛性和较强的抗负载变化能力.
6. 结论
本文利用饱和有限时间控制和自适应控制理论设计出一类新的快速自适应降压控制算法, 使得即使负载未知情况下输出电压仍可以在有限时间内快速达到参考电压.通过构造Lyapunov函数从理论上严格证明了系统的全局有限时间稳定性.最后通过仿真对比, 验证了所提方法的有效性.
-
图 4 锂离子电池等效的一阶RC并联电路模型
Fig. 4 Lithium-ion battery equivalent model based on flrst-order RC parallel
图 5 等效一阶RC并联电路结构的SC模型
Fig. 5 SC equivalent model based on flrst-order RC parallel circuit
图 7 PSO-PI实时优化的"$\lambda $-控制"框图
Fig. 7 PSO-PI real-time optimization "$\lambda $-control" block diagram
图 11 PMP算法能量优化前后对比图
Fig. 11 After before the comparison chart of PMP energy optimization algorithm
图 12 PSO-PI控制器实时优化Hamiltonian函数出力系数$ \lambda (t) $曲线图
Fig. 12 Graph of output coe–cient real-time optimization of Hamiltonian function by PSO-PI controller
图 13 单一锂离子电池和Li-SC HESS SOC仿真情况对比
Fig. 13 Comparison of single lithium-ion battery and Li-SC HESS SOC simulation
-
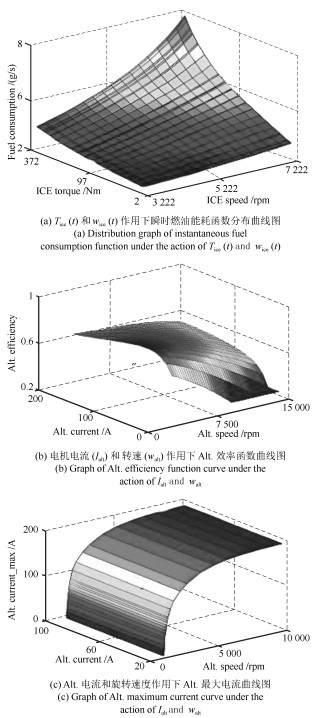
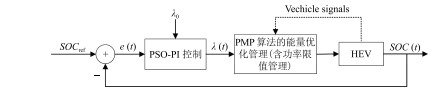
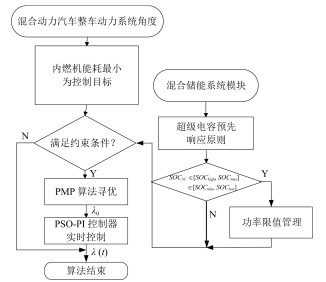
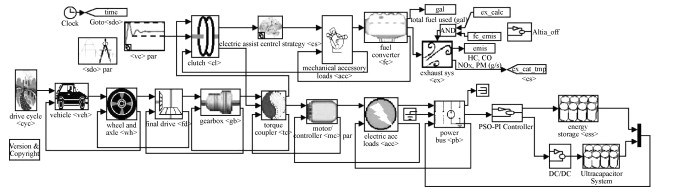
[1] 赵秀春, 郭戈.混合动力电动汽车能量管理策略研究综述.自动化学报, 2006, 42(3):321-334 http://www.aas.net.cn/CN/abstract/abstract18823.shtmlZhao Xiu-Chun, Guo Ge. Survey on energy management strategies for hybrid electric vehicles. Acta Automatica Sinica, 2016, 42(3):321-334 http://www.aas.net.cn/CN/abstract/abstract18823.shtml [2] Kim T, Qiao W, Qu L Y. Real-time state of charge and electrical impedance estimation for lithium-ion batteries based on a hybrid battery model. In:Proceedings of the 2013 Annual IEEE Applied Power Electronics Conference and Exposition. Long Beach, USA:IEEE, 2013. 563-568 [3] 杨培刚, 周育才, 刘志强, 贾光瑞, 熊少华.基于ADVISOR的纯电动汽车复合电源建模与仿真.电力科学与技术学报, 2015, 30(3):66-71 doi: 10.3969/j.issn.1673-9140.2015.03.010Yang Pei-Gang, Zhou Yu-Cai, Liu Zhi-Qiang, Jia Guang-Rui, Xiong Shao-Hua. Modeling and simulation of pure electric vehicle with composite power source based on ADVISOR. Journal of Electric Power Science and Technology, 2015, 30(3):66-71 doi: 10.3969/j.issn.1673-9140.2015.03.010 [4] Chang W Y. Estimation of the state of charge for a LFP battery using a hybrid method that combines a RBF neural network, an OLS algorithm and AGA. International Journal of Electrical Power and Energy Systems, 2013, 53:603-611 doi: 10.1016/j.ijepes.2013.05.038 [5] Gan M, Peng H, Dong X P. A hybrid algorithm to optimize RBF network architecture and parameters for nonlinear time series prediction. Applied Mathematical Modelling, 2012, 36(7):2911-2919 doi: 10.1016/j.apm.2011.09.066 [6] Sharafi M, ELMekkawy T Y. Multi-objective optimal design of hybrid renewable energy systems using PSO-simulation based approach. Renewable Energy, 2014, 68:67-79 doi: 10.1016/j.renene.2014.01.011 [7] 许世景, 吴志新.基于PMP的HEV全局最优能量管理策略研究.中国机械工程, 2014, 25(1):138-141 doi: 10.3969/j.issn.1004-132X.2014.01.026Xu Shi-Jing, Wu Zhi-Xin. Investigation of global optimization energy management strategy of HEV based on PMP. China Mechanical Engineering, 2014, 25(1):138-141 doi: 10.3969/j.issn.1004-132X.2014.01.026 [8] 夏超英, 张聪.混合动力系统能量管理策略的实时优化控制算法.自动化学报, 2015, 41(3):508-517 http://www.aas.net.cn/CN/abstract/abstract18629.shtmlXia Chao-Ying, Zhang Cong. Real-time optimization control algorithm of energy management strategy for hybrid electric vehicles. Acta Automatica Sinica, 2015, 41(3):508-517 http://www.aas.net.cn/CN/abstract/abstract18629.shtml [9] Santucci A, Sorniotti A, Lekakou C. Power split strategies for hybrid energy storage systems for vehicular applications. Journal of Power Sources, 2014, 258:395-407 doi: 10.1016/j.jpowsour.2014.01.118 [10] Masih-Tehrani M, Ha'iri-Yazdi M R, Esfahanian V, Safaei A. Optimum sizing and optimum energy management of a hybrid energy storage system for lithium battery life improvement. Journal of Power Sources, 2013, 244:2-10 doi: 10.1016/j.jpowsour.2013.04.154 [11] Schneider M, Biel K, Pfaller S, Schaede H, Rinderknecht S, Glock C H. Optimal sizing of electrical energy storage systems using inventory models. Energy Procedia, 2015, 73:48-58 doi: 10.1016/j.egypro.2015.07.559 [12] 张培建, 吴建国.基于在线辨识的特征模型预测函数控制研究.计算机仿真, 2010, 27(11):299-302 doi: 10.3969/j.issn.1006-9348.2010.11.076Zhang Pei-Jian, Wu Jian-Guo. Research of characteristic model predictive functional control based on on-line identification. Computer Simulation, 2010, 27(11):299-302 doi: 10.3969/j.issn.1006-9348.2010.11.076 [13] Su X Y, Zhou W S, von Bally G, Vukicevic D. Automated phase-measuring profilometry using defocused projection of a Ronchi grating. Optics Communications, 1992, 94(6):561-573 doi: 10.1016/0030-4018(92)90606-R [14] 夏超英, 杜智明.丰田PRIUS混合动力汽车能量优化管理策略仿真分析.吉林大学学报(工学版), 2017, 47(2):373-383 http://d.old.wanfangdata.com.cn/Periodical/jlgydxzrkxxb201702005Xia Chao-Ying, Du Zhi-Ming. Simulation analysis on energy optimization strategy for Toyota PRIUS hybrid electric vehicle. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(2):373-383 http://d.old.wanfangdata.com.cn/Periodical/jlgydxzrkxxb201702005 [15] 秦大同, 杨官龙, 刘永刚, 林毓培.插电式混合动力汽车能耗优化控制策略的研究.汽车工程, 2015, 37(12):1366-1370, 1377 doi: 10.3969/j.issn.1000-680X.2015.12.002Qin Da-Tong, Yang Guan-Long, Liu Yong-Gang, Lin Yu-Pei. A research on energy consumption optimization control strategy for plug-in hybrid electric vehicle. Automotive Engineering, 2015, 37(12):1366-1370, 1377 doi: 10.3969/j.issn.1000-680X.2015.12.002 [16] 雷嗣军, 宋小文.遗传算法与ADVISOR联合优化仿真汽车动力传动系统.机械科学与技术, 2010, 29(9):1137-1141 http://www.cnki.com.cn/Article/CJFDTOTAL-JXKX201009003.htmLei Si-Jun, Song Xiao-Wen. Optimization of an automobile transmission system with genetic algorithm and ADVISOR. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(9):1137-1141 http://www.cnki.com.cn/Article/CJFDTOTAL-JXKX201009003.htm [17] 李宝磊, 施心陵, 苟常兴, 吕丹桔, 安镇宙, 张榆锋.多元优化算法及其收敛性分析.自动化学报, 2015, 41(5):949-959 http://www.aas.net.cn/CN/abstract/abstract18669.shtmlLi Bao-Lei, Shi Xin-Ling, Gou Chang-Xing, Lv Dan-Ju, An Zhen-Zhou, Zhang Yu-Feng. Multivariant optimization algorithm and its convergence analysis. Acta Automatica Sinica, 2015, 41(5):949-959 http://www.aas.net.cn/CN/abstract/abstract18669.shtml [18] 王琪, 孙玉坤, 黄永红.一种蓄电池-超级电容器复合电源型混合动力汽车制动力分配策略研究.电工技术学报, 2014, 29(S1):155-163 http://d.old.wanfangdata.com.cn/Conference/8625048Wang Qi, Sun Yu-Kun, Huang Yong-Hong. Research on a distribution strategy of braking force used in hybrid electric vehicles with battery-ultracapacitor hybrid energy storage system. Transactions of China Electrotechnical Society, 2014, 29(S1):155-163 http://d.old.wanfangdata.com.cn/Conference/8625048 -
下载:
下载:
计量
- 文章访问数: 2621
- HTML全文浏览量: 397
- PDF下载量: 661
- 被引次数: 0
