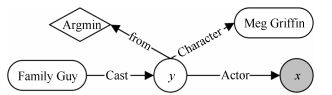
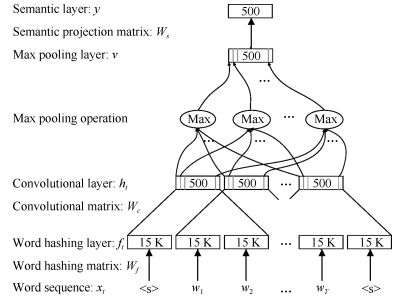
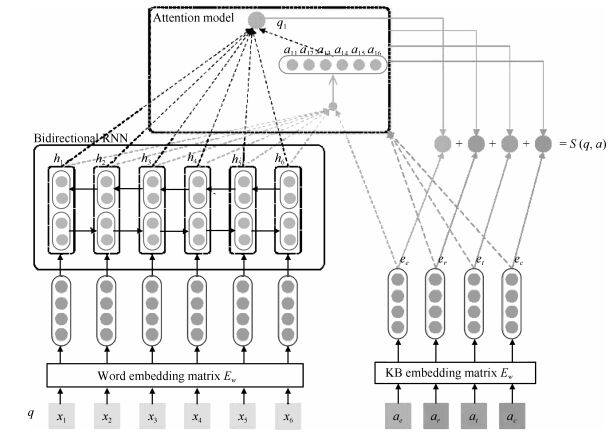
-
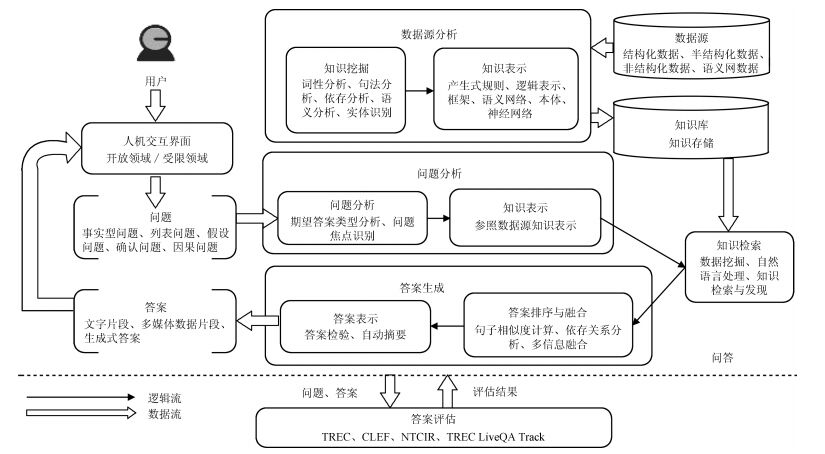
摘要: 将自动问答系统从基于文本关键词的层面,提升到基于知识的层面,实现个性化、智能化的知识机器人,已成为自动问答系统未来的发展趋势与目标.本文从知识管理的角度出发,分析和总结自动问答领域的最新研究成果.按照知识表示方法,对代表性自动问答系统及关键问题进行了描述和分析;并对主流的英文、中文自动问答应用和主要评测方法进行了介绍.Abstract: Question answering systems are evolving from the text keywords level to the next knowledge-based level, and thus realizing personalized and intelligent knowledge robots has become the development trend and goal for the future question answering systems. From the viewpoint of knowledge management, this paper analyzes and summarizes the latest research findings in the field of automatic question answering. According to the knowledge representation methods, this paper surveys several representative question answering systems and analyzes their key technologies. Also investigated are some mainstream English and Chinese-language-based question answering applications and the commonly used evaluation methods.1) 本文责任编委 王飞跃
-
表 1 典型英文自动问答系统
Table 1 A list of English QA systems
问答系统 问题类型 数据源 答案形式 相关技术 START What, Who, When等开头的事实型或者定义型问题 START KB、Internet Public Library 一句话或者一段文字 自然语言注释(Natural language annotations)、句子级别的自然语言处理(Sentence-level NLP) AnswerBus 开放领域问答系统 互联网 按照相关程度返回若干个可能的候选答案语句 命名实体抽取(Named entities extraction) Evi 开放领域问答系统 自有结构化知识库(Structured knowledge base), Yelp和第三方网站的数据和API 类似人类语言风格的简明回答 知识表示 AskJeeves 开放领域问答系统 自有问答数据库、互联网 文本、文档链接以及内容摘要 自然语言检索技术(NLP)、人工操作目录索引 Wolfram Alpha 开放领域问答系统 内置的结构化知识库 包含答案信息的各种数据和图表 计算知识引擎(Computational knowledge) Watson 开放领域问答系统 定义了自身的知识框架, 并从海量结构化和半结构化资料中抽取知识构建知识体系 针对用户提问的精准回答 统计机器学习、句法分析、主题分析、信息抽取、知识库集成和知识推理 表 2 典型中文自动问答系统
Table 2 A list of Chinese QA systems
问答系统 问题类型 数据源 答案形式 相关技术 微软小冰 日常聊天伴侣 海量网民聊天语料库 拟人化回答 情感计算、自主知识学习、意图对接对话引擎 京东JIMI 电商售前、售后咨询 自有问答库 文本 深度神经网络、意图识别、命名实体识别 小i机器人 业务咨询 语言知识库以及业务知识库 文本 知识表示、本体理论、分领域的语义网络 度秘 生活服务类咨询 互联网 服务推荐(如餐厅、影院) 全网数据挖掘和聚合 阿里小蜜 导购咨询 自有语料库 文本、语音、网页链接等 知识图谱、语义理解、个性化推荐、深度学习 -
[1] 王飞跃.软件定义的系统与知识自动化:从牛顿到默顿的平行升华.自动化学报, 2013, 41(1): 1-8 http://www.aas.net.cn/CN/abstract/abstract18578.shtmlWang Fei-Yue. Software-defined systems and knowledge automation: a parallel paradigm shift from newton to merton. Acta Automatica Sinica, 2013, 41(1): 1-8 http://www.aas.net.cn/CN/abstract/abstract18578.shtml [2] 王飞跃.机器人的未来发展:从工业自动化到知识自动化.科技导报, 2015, 33(21): 39-44 http://www.cnki.com.cn/Article/CJFDTOTAL-KJDB201521012.htmWang Fei-Yue. On future development of robotics: from industrial automation to knowledge automation. Science & Technology Review, 2015, 33(21): 39-44 http://www.cnki.com.cn/Article/CJFDTOTAL-KJDB201521012.htm [3] Bidian C, Evans M M, Dalkir K. A holistic view of the knowledge life cycle: The Knowledge Management Cycle (KMC) model. Electronic Journal of Knowledge Management, 2014, 12: 85-97 http://www.ejkm.com/issue/download.html?idArticle=563 [4] Simmons R. Answering English questions by computer: a survey. Communications of the ACM, 1965, 8(1): 53-70 doi: 10.1145/363707.363732 [5] Androutsopoulos I, Ritchie G D, Thanisch P. Natural language interfaces to databases—an introduction. Natural Language Engineering, 1995, 1(1): 29-81 http://journals.cambridge.org/action/displayFulltext?type=1&pdftype=1&fid=1313064&volumeId=1&issueId=01&aid=1313056 [6] Indurkhya N, Damerau F J. Handbook of Natural Language Processing (Second Edition). Florida: CRC Press, 2010 [7] 郑实福, 刘挺, 秦兵, 李生.自动问答综述.中文信息学报, 2002, 16(6): 46-52 http://www.cnki.com.cn/Article/CJFDTOTAL-SDKY200704020.htmZheng Shi-Fu, Liu Ting, Qin Bing, Li Sheng. Overview of question-answering. Journal of Chinese Information Processing, 2002, 16(6): 46-52 http://www.cnki.com.cn/Article/CJFDTOTAL-SDKY200704020.htm [8] 汤庸, 林鹭贤, 罗烨敏, 潘炎.基于自动问答系统的信息检索技术研究进展.计算机应用, 2008, 28(11): 2745-2748 http://www.cnki.com.cn/Article/CJFDTOTAL-JSJY200811005.htmTang Yong, Lin Lu-Xian, Luo Ye-Min, Pan Yan. Survey on information retrieval system based on question answering system. Computer Applications, 2008, 28(11): 2745-2748 http://www.cnki.com.cn/Article/CJFDTOTAL-JSJY200811005.htm [9] Bouziane A, Bouchiha D, Doumi N, Malki M. Question answering systems: survey and trends. Procedia Computer Science, 2015, 73: 366-375 doi: 10.1016/j.procs.2015.12.005 [10] Mishra A, Jain S K. A survey on question answering systems with classification. Journal of King Saud University-Computer and Information Sciences, 2016, 28 (3): 345-361 doi: 10.1016/j.jksuci.2014.10.007 [11] Burger J, Cardie C, Chaudhri V, Gaizauskas R, Harabagiu S, Israel D, Jacquemin C, Lin C Y, Maiorano S, Miller G, Moldovan D, Ogden B, Prager J, Riloff E, Singhal A, Shrihari R, Strzalkowski T, Voorhees E M, Weishedel R. Issues, tasks and program structures to roadmap research in question & answering (Q&A). Document Understanding Conferences Roadmapping Documents, 2001. 1-35 [12] 黄昌宁.从IBM深度问答系统战胜顶尖人类选手所想到的.中文信息学报, 2011, 25(6): 21-25 http://www.cnki.com.cn/Article/CJFDTOTAL-MESS201106002.htmHuang Chang-Ning. Thinking about DeepQA beating human champions. Journal of Chinese Information Processing, 2011, 25(6): 21-25 http://www.cnki.com.cn/Article/CJFDTOTAL-MESS201106002.htm [13] 毛先领, 李晓明.问答系统研究综述.计算机科学与探索, 2012, 6(3): 193-207 http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGZR200208001041.htmMao Xian-Ling, Li Xiao-Ming. A survey on question and answering systems. Journal of Frontiers of Computer Science and Technology, 2012, 6(3): 193-207 http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGZR200208001041.htm [14] 崔桓, 蔡东风, 苗雪雷.基于网络的中文问答系统及信息抽取算法研究.中文信息学报, 2004, 18(3): 24-31 http://www.cnki.com.cn/Article/CJFDTOTAL-MESS200403003.htmCui Huan, Cai Dong-Feng, Miao Xue-Lei. Research on web-based Chinese question answering system and answer extraction. Journal of Chinese Information Processing, 2004, 18(3): 24-31 http://www.cnki.com.cn/Article/CJFDTOTAL-MESS200403003.htm [15] Green B F, Wolf A K, Chomsky C, Laughery K. Baseball, an automatic question-answerer. In: Proceedings of the Western Joint IRE-AIEE-ACM Computer Conference. Los Angeles, California, USA: ACM, 1961. 219-224 [16] Woods W A, Kaplan A M, Nash-Webber B. The lunar sciences natural language information system. Journal of Neuroimmunology, 1972, 174(1-2): 32-38 [17] Hendrix G G, Sacerdoti E D, Sagalowicz D, Slocum J. Developing a natural language interface to complex data. ACM Transactions on Database Systems, 1978, 3(2): 105-147 doi: 10.1145/320251.320253 [18] Warren D H D, Pereira F C N. An efficient easily adaptable system for interpreting natural language queries. Computational Linguistics, 1982, 8(3-4): 110-122 http://dl.acm.org/citation.cfm?id=972944&picked=formats [19] Thompson B H, Thompson F B. Introducing ask, a simple knowledgeable system. In: Proceedings of the 1st Conference on Applied Natural Language Processing. Santa Monica, USA: ACL, 1983. 17-24 [20] Grosz B J, Appelt D E, Martin P A, Pereira F C N. Team: an experiment in the design of transportable natural-language interfaces. Artificial Intelligence, 1987, 32(2): 173-243 doi: 10.1016/0004-3702(87)90011-7 [21] Ott N. Aspects of the automatic generation of SQL statements in a natural language query interface. Information Systems, 1992, 17(2): 147-159 doi: 10.1016/0306-4379(92)90009-C [22] Hindle D. An analogical parser for restricted domains. In: Proceedings of the Workshop on Speech and Natural Language. New York, USA: ACL, 1992. 150-154 [23] Popescu A M, Armanasu A, Etzioni O, Ko D, Yates A. Modern natural language interfaces to databases: composing statistical parsing with semantic tractability. In: Proceedings of the 20th international conference on Computational Linguistics. Geneva, Switzerland: ACL, 2004. Article No.141 [24] Li F, Jagadish H V. Constructing an interactive natural language interface for relational databases. Proceedings of the VLDB Endowment, 2014, 8(1): 73-84 doi: 10.14778/2735461 [25] Llopis M, Ferrández A. How to make a natural language interface to query databases accessible to everyone: an example. Computer Standards and Interfaces, 2013, 35(5): 470-481 doi: 10.1016/j.csi.2012.09.005 [26] Wang S, Meng X F, Liu S. Nchiql: a Chinese natural language query system to databases. In: Proceedings of the 1999 International Symposium on Database Applications in Non-Traditional Environments. Kyoto, Japan: IEEE, 1999. [27] Kupiec J. Murax: a robust linguistic approach for question answering using an on-line encyclopedia. In: Proceedings of the International ACM SIGIR Conference on Research and Development in Information Retrieval. New Orleans, USA: ACM, 2001. 181-190 [28] Katz B. Annotating the World Wide Web using natural language. In: Proceedings of the 5th RIAO Conference on Computer Assisted Information Searching on the Internet. Montreal, Quebec, Canada: ACM, 1997. 136-155 [29] Katz B, Borchardt G C, Felshin S. Natural language annotations for question answering. In: Proceedings of the 19th International Florida Artificial Intelligence Research Society Conference. Florida, USA: AAAI, 2006. 303-306 [30] Burke R D, Hammond K J, Kulyukin V A, Lytinen S L, Tomuro N, Schoenberg S. Question answering from frequently asked question files: experiences with the FAQ finder system. AI Magazine, 1997, 18(2): 57-66 http://www.aaai.org/ojs/index.php/aimagazine/article/view/1294/1195 [31] Hovy E, Gerber L, Hermjakob U, Junk M, Lin C Y. Question answering in webclopedia. In: Proceedings of the TREC-9 Conference. Gaithersburg, USA: NIST, 2000. 655 [32] Ittycheriah A, Franz M, Zhu W J, Ratnaparkhi A, Mammone R J. Ibm's statistical question answering system. Experimental Techniques, 2000, 33(6): 30-37(38) http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.9.9839&rep=rep1&type=pdf [33] Kwok C, Etzioni O, Weld D S. Scaling question answering to the web. ACM Transactions on Information Systems, 2001, 19(3): 242-262 doi: 10.1145/502115.502117 [34] Dumais S, Banko M, Brill E, Lin J, Ng A. Web question answering: is more always better? In: Proceedings of the 25th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. Tampere, Finland: ACM, 2002. 291-298 http://dl.acm.org/citation.cfm?id=996350.996430 [35] Khalid M A, Jijkoun V, Rijke M D. The impact of named entity normalization on information retrieval for question answering. In: Proceedings of the 30th European conference on Advances in information retrieval. Berlin, Heidelberg: Springer-Verlag, 2008: 705-710 [36] 刘亚军, 徐易.一种基于加权语义相似度模型的自动问答系统.东南大学学报(自然科学版), 2004, 34(5): 609-612 doi: 10.3969/j.issn.1001-0505.2004.05.011Liu Ya-Jun, Xu Yi. Automatic question answering system based on weighted semantic similarity model. Journal of Southeast University (Natural Science Edition), 2004, 34(5): 609-612 doi: 10.3969/j.issn.1001-0505.2004.05.011 [37] 周法国, 杨炳儒.句子相似度计算新方法及在问答系统中的应用.计算机工程与应用, 2008, 44(1): 165-167 http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200801052.htmZhou Fa-Guo, Yang Bing-Ru. New method for sentence similarity computing and its application in question answering system. Computer Engineering and Applications, 2008, 44(1): 165-167 http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200801052.htm [38] Soubbotin M M. Patterns of potential answer expressions as clues to the right answers. In: Proceedings of the 10th Text Retrieval Conference. Gaithersburg, USA: NIST, 2001. 293-302 [39] Lin D K, Pantel P. Discovery of inference rules for question-answering. Natural Language Engineering, 2001, 7(4): 343-360 http://www.patrickpantel.com/download/Papers/2001/jnle01.pdf [40] Mollá D. Learning of graph-based question answering rules. In: Proceedings of the 1st Workshop on Graph Based Methods for Natural Language Processing. New York, USA: ACL, 2006. 37-44 [41] Moldovan D, Clark C, Harabagiu S M, Maiorano S J. Cogex: a logic prover for question answering. In: Proceedings of the 2003 Conference of the North American Chapter of the Association for Computational Linguistics on Human Language Technology. Edmonton, Canada: ACL, 2003. 87-93 [42] Tang L R, Mooney R J. Using multiple clause constructors in inductive logic programming for semantic parsing. In: Proceedings of the European Conference on Machine Learning. Freiburg, Germany: Springer, 2001. 466-477 [43] Zadeh L A. Fuzzy logic = computing with words. IEEE Transactions on Fuzzy Systems, 1996, 4(2): 103-111 doi: 10.1109/91.493904 [44] Clark P, Thompson J, Porter B. A knowledge-based approach to question-answering. In: Proceedings of the 6th National Conference on Artificial Intelligence. Orlando, USA: AAAI, 1999. 43-51 [45] Barker K, Chaudhri V K, Chaw S Y, Clark P E, FAN J, Israel D, Mishra S, Porter B, Romero P, Tecuci D, Yeh P. A question-answering system for AP chemistry. In: Proceedings of the 9th International Conference on Knowledge Representation and Reasoning. Whistler, Canada: AAAI, 2004. 488-497 [46] 刘开瑛.汉语框架语义网构建及其应用技术研究.中文信息学报, 2011, 25(6): 46-53 http://www.cnki.com.cn/Article/CJFDTOTAL-MESS201106006.htmLiu Kai-Ying. Research on Chinese FrameNet construction and application technologies. Journal of Chinese Information Processing, 2011, 25(6): 46-53 http://www.cnki.com.cn/Article/CJFDTOTAL-MESS201106006.htm [47] 王智强, 李茹, 梁吉业, 张旭华, 武娟, 苏娜.基于汉语篇章框架语义分析的阅读理解问答研究.计算机学报, 2016, 38(4): 795-807 doi: 10.11897/SP.J.1016.2016.00795Wang Zhi-Qiang, Li Ru, Liang Ji-Ye, Zhang Xu-Hua, Wu Juan, Su Na. Research on question answering for reading comprehension based on Chinese discourse frame semantic parsing. Chinese Journal of Computers, 2016, 38(4): 795-807 doi: 10.11897/SP.J.1016.2016.00795 [48] Bollacker K, Evans C, Paritosh P, Sturge T, Taylor J. Freebase: a collaboratively created graph database for structuring human knowledge. In: Proceedings of the ACM SIGMOD International Conference on Management of Data. Vancouver, Canada: ACM, 2008. 1247-1250 [49] Suchanek F M, Kasneci G, Weikum G. Yago: a core of semantic knowledge. In: Proceedings of the 16th International Conference on World Wide Web. Banff, Canada: WWW, 2007. 697-706 [50] Hoffart J, Suchanek F M, Berberich K, Weikum G. Yago2: a spatially and temporally enhanced knowledge base from wikipedia. Artificial Intelligence, 2013, 194: 28-61 doi: 10.1016/j.artint.2012.06.001 [51] Yao X C, Van Durme B. Information extraction over structured data: question answering with freebase. In: Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics. Baltimore, USA: ACL, 2014. 956-966 [52] Yih W T, Chang M W, He X D, Gao J F. Semantic parsing via staged query graph generation: question answering with knowledge base. In: Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing of the AFNLP. Beijing, China: ACL, 2015.1321-1331 [53] West R, Gabrilovich E, Murphy K, Sun S, Gupta R, Lin D K. Knowledge base completion via search-based question answering. In: Proceedings of the 23rd International Conference on Worldwide Web. Seoul, Korea: ACM, 2014. 515-526 [54] Unger C, Cimiano P. Pythia: compositional meaning construction for ontology-based question answering on the semantic web. In: Proceedings of the Natural Language Processing and Information Systems-International Conference on Applications of Natural Language to Information Systems. Alicante, Spain: Springer, 2011. 153-160 [55] 周永梅, 陶红, 陈姣姣, 张再跃.自动问答系统中的句子相似度算法的研究.计算机技术与发展, 2012, 22(5): 75-78 http://www.cnki.com.cn/Article/CJFDTOTAL-WJFZ201205020.htmZhou Yong-Mei, Tao Hong, Chen Jiao-Jiao, Zhang Zai-Yue. Study on sentence similarity approach of Automatic Ask & Answer System. Computer Technology and Development, 2012, 22(5): 75-78 http://www.cnki.com.cn/Article/CJFDTOTAL-WJFZ201205020.htm [56] 杜文华.本体构建方法比较研究.情报杂志, 2005, 24(10): 24-25 doi: 10.3969/j.issn.1002-1965.2005.10.008Du Wen-Hua. Comparative study of ontology construction methods. Journal of Information, 2005, 24(10): 24-25 doi: 10.3969/j.issn.1002-1965.2005.10.008 [57] 魏顺平, 何克抗.基于文本挖掘的领域本体半自动构建方法研究——以教学设计学科领域本体建设为例.开放教育研究, 2008, 14(5): 95-101 http://www.cnki.com.cn/Article/CJFDTOTAL-JFJJ200805019.htmWei Shun-Ping, He Ke-Kang. Semi-automatic building approach of domain ontology based on text mining——a case study of building instructional design domain ontology. Open Education Research, 2008, 14(5): 95-101 http://www.cnki.com.cn/Article/CJFDTOTAL-JFJJ200805019.htm [58] Iyyer M, Boyd-Graber J, Claudino L, Socher R, Iii H D. A neural network for factoid question answering over paragraphs. In: Proceedings of the Conference on Empirical Methods in Natural Language Processing. Doha, Qatar: ACL, 2014. 633-644 [59] Yih W T, He X D, Meek C. Semantic parsing for single-relation question answering. In: Proceedings of the Meeting of the Association for Computational Linguistics. Baltimore, USA: ACL, 2014. 643-648 [60] Zhang Y Z, Liu K, He S Z, Ji G L, Liu Z Y, Wu H, Zhao J. Question answering over knowledge base with neural attention combining global knowledge information. arXiv: 1606.00979, 2016. [61] Werbos P J. Beyond Regression: new Tools for Prediction and Analysis in the Behavioral Science [Ph.D. dissertation], Harvard University, USA, 1974 [62] Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets. Neural Computation, 2006, 18(7): 1527-1554 doi: 10.1162/neco.2006.18.7.1527 [63] Silver D, Huang A, Maddison C J, Guez A, Sifre L, Van Den Driessche G, Schrittwieser J, Antonoglou I, Panneershelvam V, Lanctot M, Dieleman S, Grewe D, Nham J, Kalchbrenner N, Sutskever I, Lillicrap T, Leach M, Kavukcuoglu K, Graepel T, Hassabis D. Mastering the game of go with deep neural networks and tree search. Nature, 2016, 529(7587): 484-489 doi: 10.1038/nature16961 [64] 刘康, 张元哲, 纪国良, 来斯惟, 赵军.基于表示学习的知识库问答研究进展与展望.自动化学报, 2016, 42(6): 807-818 http://www.aas.net.cn/CN/abstract/abstract18872.shtmlLiu Kang, Zhang Yuan-Zhe, Ji Guo-Liang, Lai Si-Wei, Zhao Jun. Representation learning for question answering over knowledge base: an overview. Acta Automatica Sinica, 2016, 42(6): 807-818 http://www.aas.net.cn/CN/abstract/abstract18872.shtml [65] Zheng Z P. AnswerBus question answering system. In: Proceedings of the 2nd International Conference on Human Language Technology Research. San Diego, USA: ACM, 2002. 399-404 [66] Tunstall-Pedoe W. True knowledge: open-domain question answering using structured knowledge and inference. AI Magazine, 2010, 31(3): 80-92 doi: 10.1609/aimag.v31i3.2298 [67] Hajishirzi H, Mueller E T. Question answering in natural language narratives using symbolic probabilistic reasoning. In: Proceedings of the 25th International Florida Articial Intelligence Research Society Conference. Marco Island, USA: AAAI, 2012. 38-43 [68] Lally A, Prager J M, McCord M C, Boguraev B K, Patwardhan S, Fan J, FODOR P, Chu-Ca J. Question analysis: how watson reads a clue. IBM Journal of Research and Development, 2012, 56(3-4): 2:1-2:14 http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&tp=&arnumber=6177727 [69] Kalyanpur A, Patwardhan S, Boguraev B K, Lally A, Chu-Carroll J. Fact-based question decomposition in DeePQA. IBM Journal of Research and Development, 2012, 56(3): 388-389 http://ieeexplore.ieee.org/xpl/abstractKeywords.jsp?reload=true&arnumber=6177726&filter%3DAND%28p_IS_Number%3A6177717%29 [70] Gondek D C, Lally A, Kalyanpur A, Murdock J W, Duboue P A, Zhang L, Pan Y, Qiu Z M. A framework for merging and ranking of answers in DeePQA. IBM Journal of Research and Development, 2012, 56(3-4): 14:1-14:12 http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6177810& [71] Dang H T, Kelly D, Lin J J. Overview of the TREC 2007 question answering track. In: Proceedings of the 16th Text Retrieval Conference. Gaithersburg, USA: NIST, 2007. 115-123 [72] Olvera-Lobo M D, Gutiérrez-Artacho J. Question answering track evaluation in TREC, CLEF and NTCIR. Advances in Intelligent Systems and Computing, 2015, 353: 13-22 doi: 10.1007/978-3-319-16486-1 [73] Peñas A, Forner P, Sutcliffe R, Rodrigo Á, Forăscu C, Alegria I, Giampiccolo D, Moreau N, Osenova P. Overview of ResPubliQA 2009: question answering evaluation over European legislation. In: Proceedings of the 10th Cross-Language Evaluation Forum Conference on Multilingual Information Access Evaluation: text Retrieval Experiments. Corfu, Greece: Springer, 2010. 174-196 [74] Agichtein E, Carmel D, Harman D, Pelleg D, Pinter Y. Overview of the TREC 2015 LiveQA track. In: Proceedings of the 24th TextREtrieval Conference. Gaithersburg, USA: NIST, 2015. 1-9 -




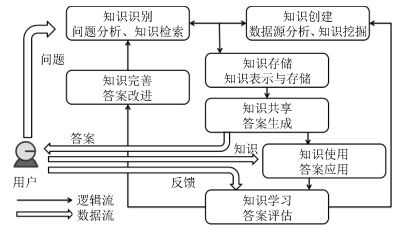
 下载:
下载: