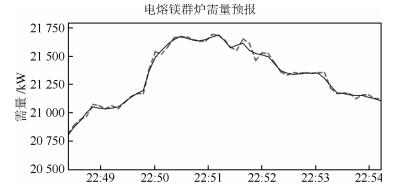
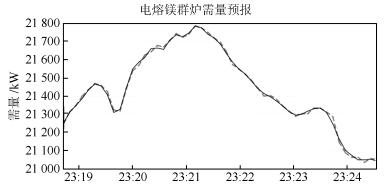
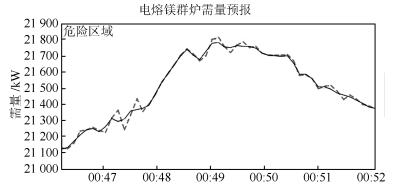
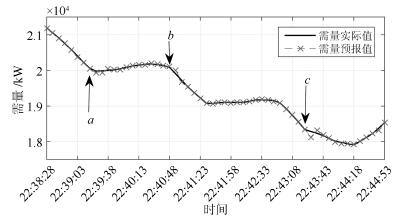
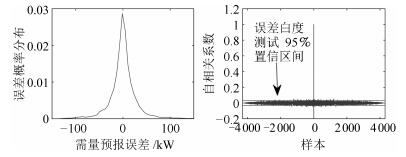
-
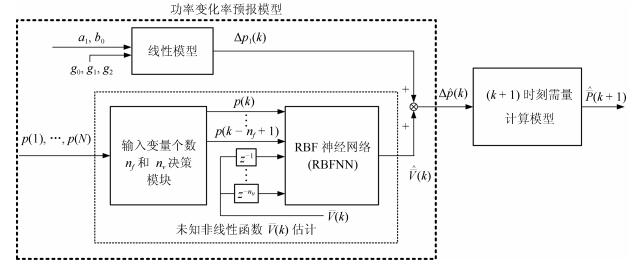
摘要: 电熔镁群炉需量指当前时刻k和(k-1),…,(k-n+1)时刻群炉功率的平均值,用于度量高耗能电熔镁群炉用电量.(k+1)时刻群炉需量取决于功率变化率.本文建立了功率变化率与电流控制系统输出电流之间由线性项与未知非线性项组成的动态模型,其中线性项通过电流被控对象的参数和控制器的参数计算,未知非线性项采用基于偏自相关函数(Partial autocorrelation function,PACF)输入变量决策的径向基函数神经网络(Radial basis function neural network,RBFNN)来估计.本文提出了由当前k时刻的需量和功率,(k-n+1)时刻功率及k时刻功率变化率的估计组成的(k+1)时刻需量的计算模型.通过某电熔镁砂厂实际数据的仿真实验和工业实验表明所提方法可准确预报需量变化趋势,可以防止因原料变化引起需量尖峰导致错误切断电熔镁炉供电造成电熔镁砂质量降低.Abstract: The demand of fused magnesium furnace group (FMFG) is the average value of powers at times k, (k-1), …, (k-n+1). The demand indicates the electricity consumption of the FMFG. The demand at time (k+1) depends on the rate of power change. In this paper, we develop a dynamic model of the rate of power change and the output current. The model consists of a linear term and an unknown nonlinear term, where the linear term can be calculated by the parameters of the controlled current and the controller, and the unknown nonlinear term can be estimated using the radial basis function neural network (RBFNN). The input variables of RBFNN are decided based on partial autocorrelation function (PACF). Then a computing model of demand at time (k+1) is proposed, which consists of the demand at time k, the powers at times k and (k-n+1) and the estimate of the rate of power change at time k. Simulations based on actual data and industrial experiments at a fused magnesia plant show that the proposed method can accurately forecast demand trends and can prevent reduction of fused magnesia grade caused by unnecessary cut off due to the demand spikes caused by change of raw materials.1) 本文责任编委 张卫东
-
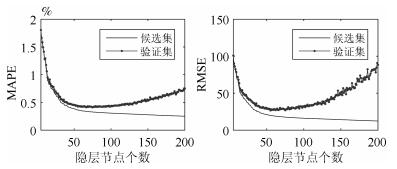
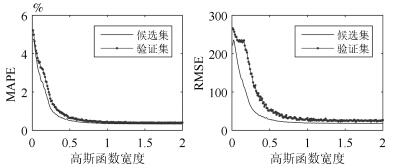
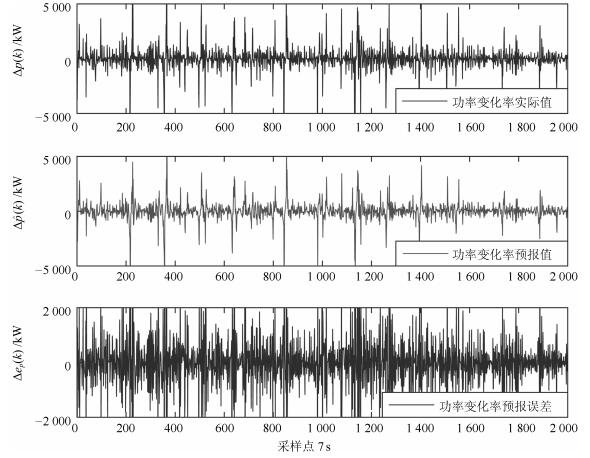
表 1 ∆p(k)预报误差指标
Table 1 Forecast error indicators of ∆p(k)
方差 RMSE 1.1481E+6 1 071.3 表 2 需量预报误差指标
Table 2 Forecast error indicators of demand
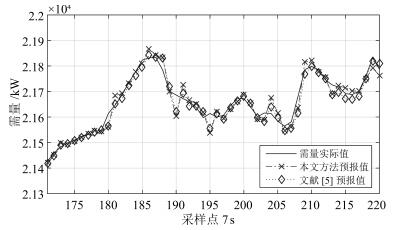
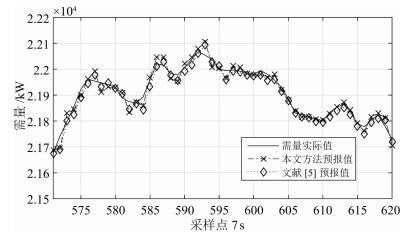
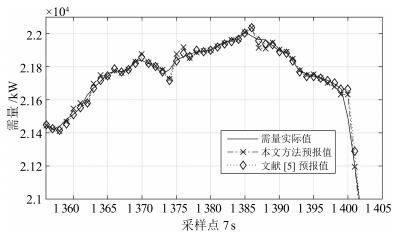
方法 方差 PB (%) RMSE MAPE (%) 文献[5] 1 533.0 97.05 39.1921 0.0979 本文 1 275.7 97.55 35.7104 0.1054 表 3 超限拉闸时段需量预报误差
Table 3 Demand forecast errors during cut off time period
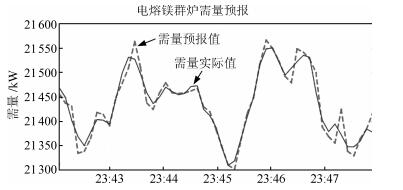
时间 需量实际值(kW) 需量预报值(kW) 误差(kW) 22 : 36 : 50 21 626 21 635 -9 22 : 36 : 57 21 654 21 650 4 22 : 37 : 04 21 692 21 685 7 22 : 37 : 11 21 728 21 725 3 22 : 37 : 18 21 754 21 751 4 22 : 37 : 25 21 788 21 787 1 22 : 37 : 32 21 812 21 829 -17 22 : 37 : 39 21 834 21 849 -15 22 : 37 : 46 21 835 21 839 -4 22 : 37 : 53 21 833 21 829 4 22 : 38 : 00 21 826 21 822 4 22 : 38 : 07 21 691 21 819 -128 22 : 38 : 14 21 510 21 463 47 22 : 38 : 21 21 335 21 318 17 22 : 38 : 28 21 191 21 176 15 22 : 38 : 35 21 049 21 056 -7 22 : 38 : 42 20 908 20 907 1 22 : 38 : 49 20 751 20 769 -18 22 : 38 : 56 20 581 20 577 4 22 : 39 : 03 20 407 20 385 22 表 4 工业实验需量预报误差指标
Table 4 Demand forecast error indicators of industrial experiment
方差 PB (%) RMSE MAPE 1 049.8 97.68 32.3981 0.0996 -
[1] Paparoditis E, Sapatinas T. Short-term load forecasting:the similar shape functional time-series predictor. IEEE Transactions on Power Systems, 2013, 28(4):3818-3825 doi: 10.1109/TPWRS.2013.2272326 [2] Ceperic E, Ceperic V, Baric A. A strategy for short-term load forecasting by support vector regression machines. IEEE Transactions on Power Systems, 2013, 28(4):4356-4364 doi: 10.1109/TPWRS.2013.2269803 [3] Quan H, Srinivasan D, Khosravi A. Short-term load and wind power forecasting using neural network-based prediction intervals. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(2):303-315 doi: 10.1109/TNNLS.2013.2276053 [4] Kebriaei H, Araabi B N, Rahimi-Kian A. Short-term load forecasting with a new nonsymmetric penalty function. IEEE Transactions on Power Systems, 2011, 26(4):1817-1825 doi: 10.1109/TPWRS.2011.2142330 [5] Yang J, Chai T Y. Data-driven demand forecasting method for fused magnesium furnaces. In: Proceedings of the 12th World Congress on Intelligent Control and Automation. Guilin, China: IEEE, 2016. 2015-2022 http://ieeexplore.ieee.org/document/7578831/ [6] Wu Z, Chai T Y, Sun J. Intelligent operational feedback control for fused magnesium furnace. In: Proceedings of the 19th World Congress on International Federation of Automatic Control. Cape Town, South Africa: IFAC, 2014. 8516-8521 http://www.sciencedirect.com/science/article/pii/S1474667016429575 [7] Ozgun O, Abur A. Flicker study using a novel arc furnace model. IEEE Transactions on Power Delivery, 2002, 17(4):1158-1163 doi: 10.1109/TPWRD.2002.804013 [8] 王其平.电器电弧理论.北京:机械工业出版社, 1991.Wang Qi-Ping. Arc Theory of Electrical Appliances. Beijing:Metallurgical Industry Press, 1991. [9] Shigley J E, Mischke C R, Budynas R G. Mechanical Engineering Design. New York, USA: McGraw-Hill, 1989. [10] 郭茂先.工业电炉.北京:冶金工业出版社, 2002.Guo Mao-Xian. Industry Furnace. Beijing:Metallurgical Industry Press, 2002. [11] Wu Z W, Wu Y J, Chai T Y, Sun J. Data-driven abnormal condition identification and self-healing control system for fused magnesium furnace. IEEE Transactions on Industrial Electronics, 2015, 62(3):1703-1715 doi: 10.1109/TIE.2014.2349479 [12] Cecati C, Kolbusz J, Rózycki P, Siano P, Wilamowski B. A novel RBF training algorithm for short-term electric load forecasting and comparative studies. IEEE Transactions on Industrial Electronics, 2015, 62(10):6519-6529 doi: 10.1109/TIE.2015.2424399 [13] Yu H, Xie T T, Paszczynski S, Wilamowski B M. Advantages of radial basis function networks for dynamic system design. IEEE Transactions on Industrial Electronics, 2011, 58(12):5438-5450 doi: 10.1109/TIE.2011.2164773 [14] Xie T T, Yu H, Hewlett J, Rózycki P, Wilamowski B. Fast and efficient second-order method for training radial basis function networks. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(4):609-619 doi: 10.1109/TNNLS.2012.2185059 [15] Du K L, Swamy M N S. Radial basis function networks. Neural Networks and Statistical Learning. London, UK: Springer, 2014. 299-335 [16] Chen S, Cowan C F N, Grant P M. Orthogonal least squares learning algorithm for radial basis function networks. IEEE Transactions on Neural Networks, 1991, 2(2):302-309 doi: 10.1109/72.80341 [17] Park J, Sandberg I W. Universal approximation using radial-basis-function networks. Neural Computation, 1991, 3(2):246-257 doi: 10.1162/neco.1991.3.2.246 [18] Gomm J B, Yu D L. Selecting radial basis function network centers with recursive orthogonal least squares training. IEEE Transactions on Neural Networks, 2000, 11(2):306-314 doi: 10.1109/72.839002 [19] Armstrong J S, Collopy F. Error measures for generalizing about forecasting methods:empirical comparisons. International Journal of Forecasting, 1992, 8(1):69-80 doi: 10.1016/0169-2070(92)90008-W [20] Dai W, Chai T Y, Yang S X. Data-driven optimization control for safety operation of hematite grinding process. IEEE Transactions on Industrial Electronics, 2015, 62(5):2930-2941 doi: 10.1109/TIE.2014.2362093 [21] 代伟, 柴天佑.数据驱动的复杂磨矿过程运行优化控制方法.自动化学报, 2014, 40(9):2005-2014 http://www.aas.net.cn/CN/abstract/abstract18472.shtmlDai Wei, Chai Tian-You. Data-driven optimal operational control of complex grinding processes. Acta Automatica Sinica, 2014, 40(9):2005-2014 http://www.aas.net.cn/CN/abstract/abstract18472.shtml [22] 吴志伟, 柴天佑, 吴永建.电熔镁砂产品单吨能耗混合预报模型.自动化学报, 2013, 39(12):2002-2011 http://www.aas.net.cn/CN/abstract/abstract18239.shtmlWu Zhi-Wei, Chai Tian-You, Wu Yong-Jian. A hybrid prediction model of energy consumption per ton for fused magnesia. Acta Automatica Sinica, 2013, 39(12):2002-2011 http://www.aas.net.cn/CN/abstract/abstract18239.shtml [23] 黄宇斌, 袁景淇, 汪瑞清, 赵平伟.数据驱动的上海市日需水量预报建模研究.控制工程, 2010, 17(S2):58-60 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201003398025Huang Yu-Bin, Yuan Jing-Qi, Wang Rui-Qing, Zhao Ping-Wei. Data-driven modeling for daily water demand forecast of Shanghai city. Control Engineering of China, 2010, 17(S2):58-60 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201003398025 [24] Landau I D, Zito G. Digital Control Systems: Design, Identification and Implementation. London, UK: Springer, 2006 -




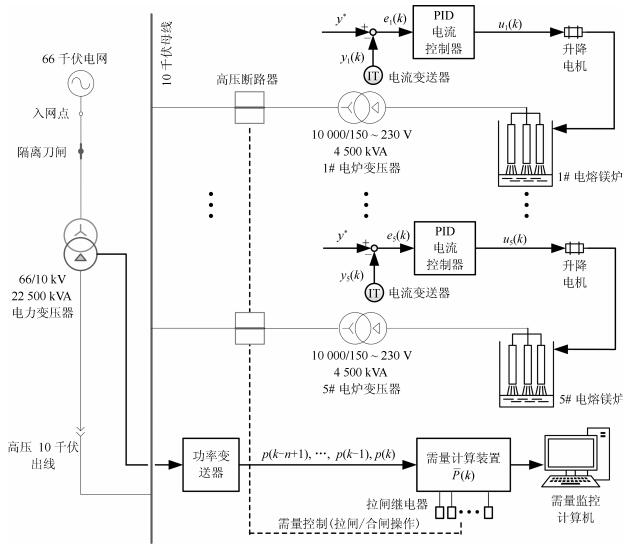
 下载:
下载: