基于混合模糊多人多目标非合作博弈的车道选择模型

王晓原; 张敬磊; 刘振雪; 尹超

doi:10.16383/j.aas.2017.c160559

基于混合模糊多人多目标非合作博弈的车道选择模型

doi: 10.16383/j.aas.2017.c160559

王晓原^1,2, ,,
张敬磊^1,,
刘振雪^1,,
尹超^1,

1.
山东理工大学交通与车辆工程学院淄博 255000
2.
清华大学汽车安全与节能国家重点实验室北京 100084

基金项目:

国家自然科学基金 61074140

山东省自然科学基金 ZR2017LF015

国家自然科学基金 51508315

山东省高等学校科技计划 J15LB07

汽车安全与节能国家重点实验室开放基金 KF16232

山东省社会科学规划研究项目 14CGLJ27

国家自然科学基金 51608313

国家自然科学基金 61573009

山东省自然科学基金 ZR2014FM027

详细信息

作者简介:
张敬磊山东理工大学交通与车辆工程学院副教授.主要研究方向为城市交通, 交通行为及安全, 智能交通系统.E-mail:jinglei@sdut.edu.cn

刘振雪山东理工大学交通与车辆工程学院硕士研究生.主要研究方向为人车环境协同智慧及控制.E-mail:liuzx321@163.com

尹超山东理工大学讲师.2015年获长安大学博士学位.主要研究方向为智能交通及公路自然灾害防治.E-mail:yinchao@sdut.edu.cn

通讯作者:
王晓原山东理工大学交通与车辆工程学院教授.主要研究方向为交通运输规划与管理, 交通信息工程及控制, 交通行为及安全, 交通流理论, 交通仿真和人车环境协同智慧及控制.本文通信作者.E-mail:wangxiaoyuan@sdut.edu.cn

计量
- 文章访问数: 2011
- HTML全文浏览量: 248
- PDF下载量: 601
- 被引次数: 58
出版历程
- 收稿日期: 2016-07-29
- 录用日期: 2016-11-28
- 刊出日期: 2017-11-20

Drivers' Lane Choice Model Based on Mixed Fuzzy Multi-person and Multi-objective Non-cooperative Game

1.
School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255000
2.
State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084

Funds:

National Natural Science Foundation of China 61074140

Natural Science Foundation of Shandong Province ZR2017LF015

National Natural Science Foundation of China 51508315

Project of Shandong Province Higher Educational Science and Technology Program J15LB07

Opening Project of the State Key Laboratory of Automotive Safety and Energy KF16232

Social Science Planning Project of Shandong Province 14CGLJ27

National Natural Science Foundation of China 51608313

National Natural Science Foundation of China 61573009

Natural Science Foundation of Shandong Province ZR2014FM027

More Information

Author Bio:
Associate professor at the School of Transportation and Vehicle Engineering, Shandong University of Technology. His research interest covers urban transportation, traffic behavior and security, and intelligent transportation systems

Master student at the School of Transportation and Vehicle Engineering, Shandong University of Technology. Her research interest covers controlling and cooperative intelligence of human-vehicle-environment

Lecturer at the School of Transportation and Vehicle Engineering, Shandong University of Technology. He received his Ph. D. degree from Chang$'$an University in 2015. His research interest covers intelligent transportation systems and highway natural disaster prevention and control

Corresponding author: WANG Xiao-Yuan Professor at the School of Transportation and Vehicle Engineering, Shandong University of Technology. His research interest covers transportation planning and management, traffic information engineering and control, traffic behavior and security, traffic flow theory, traffic simulation, and controlling and cooperative intelligence of human-vehicle-environment. Corresponding author of this paper

摘要

摘要: 建立汽车安全驾驶辅助系统（包括安全驾驶预警系统）是保证交通安全的有效手段.准确预测车辆集群态势是汽车安全辅助驾驶的前提，车道选择是车辆集群态势发生转移最为根本的原因，也是交通流理论研究的基本内容.以往研究没有综合考虑车辆集群复杂态势下各运动实体特征及其操控者类型，以及多个车道间车辆的冲突对车道选择的影响.为此，本文综合考虑各运动实体特征及其操控者类型，基于混合模糊多人多目标非合作博弈方法，建立城市快速路基本路段上的驾驶员车道选择模型.通过分析各方驾驶员在不同车道选择策略下的收益，确定换道博弈的Nash均衡，得到驾驶员最优车道选择策略.研究结果表明：基于混合模糊多人多目标非合作博弈方法建构的驾驶员车道选择模型，其预测准确率可达到85.2%.
- 智能交通系统 /
- 驾驶倾向性 /
- 车辆集群态势 /
- 多人多目标对策 /
- 混合模糊对策
Abstract: Vehicle safety driving assistance system (including driving safety alerting system) is an effective means to ensure traffic safety while accurate prediction of vehicle cluster situation is the premise of automobile safety assistant driving system. The drivers' lane choice process is not only the root cause of the transformation of vehicle cluster situation, but also the basic topic of traffic flow research. Previous studies do not synthetically consider the characteristics of individual traffic entities and the types of manipulators under the complex vehicle cluster situation, neither the influence of vehicles conflicts under multiple lanes on lane choice is taken into account. Therefore, in this paper, considering the types of vehicle manipulators and the characteristics of each movement entity, the model of drivers' lane choice on basic segment of urban expressway is built based on mixed fuzzy multi-person and multi-objective non-cooperative game. Drivers' profits under the different combinations of lane choice behaviors are analyzed, Nash equilibrium in the game process is confirmed, and the drivers' optimal lane choice strategy in a dynamic game is obtained. The results show that the model's prediction accuracy of lane change reaches 85.2%.
- Intelligent transportation systems /
- driver's tendency /
- vehicle cluster situation /
- multi-person and multi-objective decision problems /
- mixed fuzzy game
注释:

1) 本文责任编委董海荣

HTML全文

本文责任编委董海荣

图 1 三车道场景目标车所处车辆集群态势图

Fig. 1 Vehicle cluster situation for target vehicle under the three-lane condition

下载: 全尺寸图片幻灯片

图 2 三车道场景驾驶员车道选择博弈分析图

Fig. 2 Game analysis of drivers' lane choice behavior under three-lane condition

下载: 全尺寸图片幻灯片

图 3 车辆冲突类型示意图

Fig. 3 Schematic of vehicle conflicts

下载: 全尺寸图片幻灯片

图 4 冲突收益隶属函数

Fig. 4 Membership function of conflict benefit

下载: 全尺寸图片幻灯片

图 5 动态人车环境信息采集系统组成

Fig. 5 Dynamic human-vehicle-environment information acquisition systems

下载: 全尺寸图片幻灯片

图 6 驾驶模拟实验

Fig. 6 Interactive parallel virtual driving experiment

下载: 全尺寸图片幻灯片

图 7 保守型、普通型、激进型驾驶员换道频率模拟结果

Fig. 7 Simulation results of lane changing frequency for conservative, common, and radical drivers

下载: 全尺寸图片幻灯片

图 8 换道次数仿真值与实际测量值对比图

Fig. 8 Comparison of simulation and measured values in lane-changing times

下载: 全尺寸图片幻灯片

图 9 左车道、中间车道和右车道利用率仿真值与实际测量值对比图

Fig. 9 Comparison of simulation and measured values for left, middle, and right lanes in lane occupancy rate

下载: 全尺寸图片幻灯片

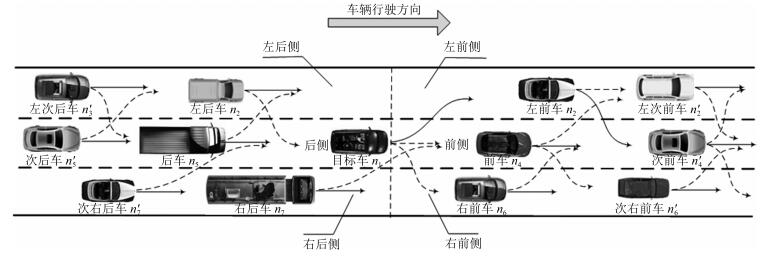
表 1 不同类型驾驶员感知各分区域车辆对目标车综合作用力的贡献率

Table 1 Contribution rates of integrated force from different types of drivers in sub-area to the target vehicle

目标车位置	目标车位于左车道						目标车位于中间车道						目标车位于右车道
贡献率驾驶员类型	$\xi _i^{ql}$	$\xi _i^{hl}$	$\xi _i^{lyq}$	$\xi _i^{lyq}$	$\xi _i^{gyq}$	$\xi _i^{gyh}$	$\xi _i^q $	$\xi _i^h $	$\xi _i^{zq} $	$\xi _i^q $	$\xi _i^h $	$\xi _i^{zq} $	$\xi _i^{ql} $	$\xi _i^{hl} $	$\xi _i^{lyq} $	$\xi _i^{lyq} $	$\xi _i^{gyq} $	$\xi _i^{gyh} $
激进型	0.244	0.161	0.186	0.226	0.086	0.097	0.219	0.152	0.166	0.219	0.152	0.166	0.244	0.161	0.186	0.226	0.086	0.097
普通型	0.251	0.201	0.181	0.193	0.081	0.093	0.226	0.187	0.152	0.226	0.187	0.152	0.251	0.201	0.181	0.193	0.081	0.093
保守型	0.265	0.236	0.173	0.168	0.076	0.082	0.241	0.191	0.111	0.241	0.191	0.111	0.265	0.236	0.173	0.168	0.076	0.082

下载: 导出CSV

表 2 冲突收益语义项与三角形模糊数之间的对应关系

Table 2 Correspondence between semantic driving conflict items and triangular fuzzy numbers

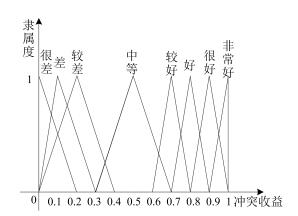
冲突收益评价语义项	三角形模糊数	冲突收益评价语义项	三角形模糊数
很差	(0, 0, 0.2)	较好	(0.6, 0.7, 0.8)
差	(0, 0.1, 0.3)	好	(0.7, 0.8, 0.9)
较差	(0, 0.2, 0.4)	很好	(0.8, 0.9, 1)
中等	(0.3, 0.5, 0.7)	非常好	(0.9, 1, 1)

下载: 导出CSV

表 3 不同类型驾驶员对各收益的模糊权重情况

Table 3 Fuzzy weight of the beneflt for difierent types of drivers

驾驶员类型	模糊权重
驾驶员类型	行车安全收益${\not{\omega }}_i^1 $	行车时间收益${\not{\omega }}_i^2$	冲突收益${\not{\omega }}_i^3 $
激进型	0.3	0.5	0.2
普通型	0.35	0.4	0.25
保守型	0.4	0.3	0.3

下载: 导出CSV

表 4 实验可采集数据

Table 4 Collected experiment data types

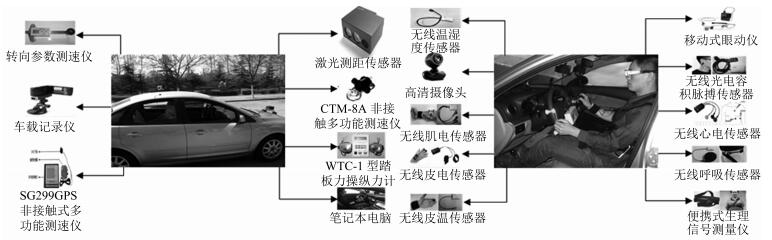
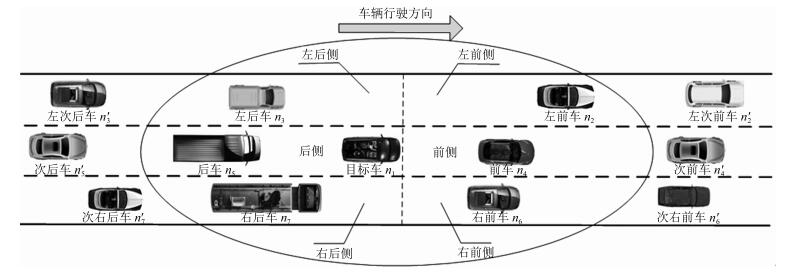
数据	目标车与周围车辆相对距离(m)						目标车与周围车辆相对速度(m/s)
数据	左前车	左后车	前车	后车	右前车	右后车	左前车	左后车	前车	后车	右前车	右后车
代码	$\Delta d_2 $	$\Delta d_3 $	$\Delta d_4 $	$\Delta d_5$	$\Delta d_6 $	$\Delta d_7 $	$\Delta v_2 $	$\Delta v_3 $	$\Delta v_4 $	$\Delta v_5 $	$\Delta v_6 $	$\Delta v_7 $

下载: 导出CSV

表 5 车道选择模型参数标定

Table 5 Parameter calibration of lane choice model

参数		$v_1 $	$v_2 $	$v_3 $	$v_4 $	$d_1 $	$d_2 $	$d_3 $	$d_4 $
数值	激进型	-3.2	-1.7	1.7	3.2	8.3	22.4	36.2	50.5
	普通型	-4.8	-2.5	2.5	4.8	12.6	25.8	40.1	60.5
	保守型	-8.7	-4.5	4.5	8.7	22.7	35.3	50.5	70.5

下载: 导出CSV

表 6 道路实车实验结果

Table 6 Verification results of actual driving experiment

驾驶员编号	预测次数	预测结果与实测结果对比		准确率(%)
驾驶员编号	预测次数	相符次数	不符次数	准确率(%)
1	80	71	9	88.8
2	80	68	12	85.0
3	80	67	13	83.8
4	80	69	11	86.3
5	80	65	15	81.3
6	80	67	13	83.8
7	80	70	10	87.5
8	80	68	12	85.0
均值	80	68.125	11.875	85.16

下载: 导出CSV

表 7 驾驶模拟实验结果

Table 7 Verification results of virtual driving experiment

驾驶员编号	预测次数	预测结果与实测结果对比		准确率(%)
驾驶员编号	预测次数	相符次数	不符次数	准确率(%)
1	80	70	10	87.5
2	80	69	11	86.3
3	80	66	14	82.5
4	80	71	9	88.8
5	80	67	13	83.8
6	80	70	10	87.5
7	80	65	15	81.3
8	80	68	12	85.0
均值	80	68.25	11.75	85.31

下载: 导出CSV

表 8 微观仿真结果与实测数据对比分析表

Table 8 Comparative analysis of microscopic simulation and measured values

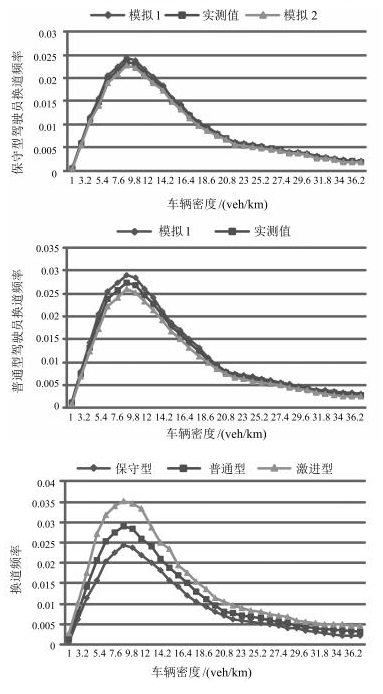
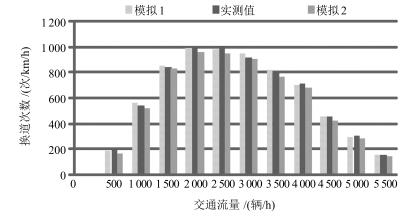
评价指标	实测值	模拟1结果	误差(%)
平均速度(m/s)	10.2	10.66	4.51
平均密度(辆/km)	19.3	18.52	4.04
平均延误(s)	7.2	6.93	3.75

下载: 导出CSV

参考文献(24)

[1]	Gipps P G. A model for the structure of lane-changing decisions. Transportation Research Part B:Methodological, 1986, 20(5):403-414 doi: 10.1016/0191-2615(86)90012-3
[2]	Hidas P. Modelling lane changing and merging in microscopic traffic simulation. Transportation Research Part C:Emerging Technologies, 2002, 10(5-6):351-371 doi: 10.1016/S0968-090X(02)00026-8
[3]	Halati A, Lieu H, Walker S. CORSIM-corridor traffic simulation model. In:Proceedings of the 1997 Traffic Congestion and Traffic Safety in the 21st Century:Challenges, Innovations, and Opportunities. New York, USA:American Society of Civil Engineers, 1997. 570-576 https://www.mendeley.com/research-papers/corsim-corridor-traffic-simulation-model/
[4]	Yang Q, Koutsopoulos H N. A microscopic traffic simulator for evaluation of dynamic traffic management systems. Transportation Research Part C:Emerging Technologies, 1996, 4(3):113-129 doi: 10.1016/S0968-090X(96)00006-X
[5]	Ahmed K I. Modeling Drivers' Acceleration and Lane Changing Behavior[Ph.D. dissertation], Massachusettes Institute of Technology, America, 1999. https://www.mendeley.com/research-papers/modeling-drivers-acceleration-lane-changing-behavior/
[6]	Toledo T. Integrated Driving Behavior Modeling[Ph.D. dissertation], Massachusettes Institute of Technology, America, 2003. http://dspace.mit.edu/handle/1721.1/29285
[7]	Keyvan-Ekbatani M, Knoop V L, Daamen W. Categorization of the lane change decision process on freeways. Transportation Research Part C:Emerging Technologies, 2016, 69:515-526 doi: 10.1016/j.trc.2015.11.012
[8]	Balal E, Cheu R L, Sarkodie-Gyan T. A binary decision model for discretionary lane changing move based on fuzzy inference system. Transportation Research Part C:Emerging Technologies, 2016, 67:47-61 doi: 10.1016/j.trc.2016.02.009
[9]	Kita H. A merging-giveway interaction model of cars in a merging section:a game theoretic analysis. Transportation Research Part A:Policy and Practice, 1999, 33(3-4):305-312 doi: 10.1016/S0965-8564(98)00039-1
[10]	杨晓芳, 张盛, 付强.基于博弈论的完全信息下的驾驶行为研究.公路交通科技, 2015, 32(7):105-111 http://d.wanfangdata.com.cn/Periodical/gljtkj201507017 Yang Xiao-Fang, Zhang Sheng, Fu Qiang. Research of driving behavior under condition of complete information based on game theory. Journal of Highway and Transportation Research and Development, 2015, 32(7):105-111 http://d.wanfangdata.com.cn/Periodical/gljtkj201507017
[11]	刘小明, 郑淑晖, 蒋新春.基于动态重复博弈的车辆换道模型.公路交通科技, 2008, 25(6):120-125 http://d.wanfangdata.com.cn/Periodical/gljtkj200806024 Liu Xiao-Ming, Zheng Shu-Hui, Jiang Xin-Chun. Lane changing model based on discrete dynamic game. Journal of Highway and Transportation Research and Development, 2008, 25(6):120-125 http://d.wanfangdata.com.cn/Periodical/gljtkj200806024
[12]	Talebpour A, Mahmassani H S, Hamdar S H. Modeling lane-changing behavior in a connected environment:a game theory approach. Transportation Research Part C:Emerging Technologies, 2015, 59:216-232 doi: 10.1016/j.trc.2015.07.007
[13]	Wang M, Hoogendoorn S P, Daamen W, van Arem B, Happee R. Game theoretic approach for predictive lane-changing and car-following control. Transportation Research Part C:Emerging Technologies, 2015, 58 (Part A):73-92 http://www.sciencedirect.com/science/article/pii/S0968090X15002491
[14]	彭金栓, 付锐, 石磊磊, 张琼.驾驶人车道变换决策分析.武汉理工大学学报, 2011, 33(12):46-50 doi: 10.3963/j.issn.1671-4431.2011.12.011 Peng Jin-Shuan, Fu Rui, Shi Lei-Lei, Zhang Qiong. Research of driver's lane change decision-making mechanism. Journal of Wuhan University of Technology, 2011, 33(12):46-50 doi: 10.3963/j.issn.1671-4431.2011.12.011
[15]	彭金栓, 付锐, 郭应时, 袁伟, 王畅.基于有限零和灰色博弈的车道变换决策分析.科技导报, 2011, 29(3):52-56 http://d.wanfangdata.com.cn/Periodical/kjdb201103012 Peng Jin-Shuan, Fu Rui, Guo Ying-Shi, Yuan Wei, Wang Chang. Analysis of lane change decision making based on the finite and zero-sum grey game theory. Science and Technology Review, 2011, 29(3):52-56 http://d.wanfangdata.com.cn/Periodical/kjdb201103012
[16]	吴磊, 王晓辉, 杨新月, 王晓原.交通态势识别及状态转换机制研究.交通标准化, 2007, (2-3):61-66 http://d.wanfangdata.com.cn/Periodical/jtbzh200702009 Wu Lei, Wang Xiao-Hui, Yang Xin-Yue, Wang Xiao-Yuan. Study on the recognition of traffic situation and its state transition mechanism. Communications Standardization, 2007, (2-3):61-66 http://d.wanfangdata.com.cn/Periodical/jtbzh200702009
[17]	Wang X Y, Zhang J L, Ban X G, Tan D R. Dynamic feature extraction method of driver's propensity under complicated vehicle group. Advances in Mechanical Engineering, 2013, 2013:1-10 doi: 10.1155/2013/287653
[18]	张青, 武东, 潘小东.有偏好信息的多目标N人非合作模糊对策及其解.山东理工大学学报(自然科学版), 2009, 23(2):24-26 http://d.wanfangdata.com.cn/Periodical/sdgcxyxb200902006 Zhang Qing, Wu Dong, Pan Xiao-Dong. Multi-objective N-person noncooperative fuzzy games with preference information and its solving method. Journal of Shandong University of Technology (Natural Science Edition), 2009, 23(2):24-26 http://d.wanfangdata.com.cn/Periodical/sdgcxyxb200902006
[19]	Xiao M, Shao X Y, Gao L, Luo Z. A new methodology for multi-objective multidisciplinary design optimization problems based on game theory. Expert Systems with Applications, 2015, 42(3):1602-1612 doi: 10.1016/j.eswa.2014.09.047
[20]	陈志旺, 白锌, 杨七, 黄兴旺, 李国强.区间多目标优化中决策空间约束、支配及同序解筛选策略.自动化学报, 2015, 41(12):2115-2124 http://www.aas.net.cn/CN/abstract/abstract18784.shtml Chen Zhi-Wang, Bai Xin, Yang Qi, Huang Xing-Wang, Li Guo-Qiang. Strategy of constraint, dominance and screening solutions with same sequence in decision space for interval multi-objective optimization. Acta Automatica Sinica, 2015, 41(12):2115-2124 http://www.aas.net.cn/CN/abstract/abstract18784.shtml
[21]	巩敦卫, 刘益萍, 孙晓燕, 韩玉艳.基于目标分解的高维多目标并行进化优化方法.自动化学报, 2015, 41(8):1438-1451 http://www.aas.net.cn/CN/abstract/abstract18718.shtml Gong Dun-Wei, Liu Yi-Ping, Sun Xiao-Yan, Han Yu-Yan. Parallel many-objective evolutionary optimization using objectives decomposition. Acta Automatica Sinica, 2015, 41(8):1438-1451 http://www.aas.net.cn/CN/abstract/abstract18718.shtml
[22]	张青, 胡子祥, 黄天民.混合模糊多目标多人非合作对策及其解.江南大学学报(自然科学版), 2005, 4(1):94-96, 108 http://d.wanfangdata.com.cn/Periodical/jiangndxxb200501022 Zhang Qing, Hu Zi-Xiang, Huang Tian-Min. Mixed fuzzy multi-objective many-person noncooperative games and its solving method. Journal of Southern Yangtze University (Natural Science Edition), 2005, 4(1):94-96, 108 http://d.wanfangdata.com.cn/Periodical/jiangndxxb200501022
[23]	Hranac R, Margiotta R, Alexiadis V. Next Generation Simulation (NGSIM) High-level Verification and Validation Plan. Washington, DC, USA:Federal Highway Administration, 2004.
[24]	Montanino M, Punzo V. Trajectory data reconstruction and simulation-based validation against macroscopic traffic patterns. Transportation Research Part B:Methodological, 2015, 80:82-106 doi: 10.1016/j.trb.2015.06.010

施引文献

期刊类型引用(29)

1.	李倩，聂简，黄鸿殿，孔庆宇，奔粤阳. 基于大脑海马认知机理的主从式AUV协同定位方法. 中国惯性技术学报. 2024(01): 27-33 . 百度学术
2.	游雄，李科，田江鹏，杨剑，余岸竹，贾奋励. 机器地图信息加工模型. 武汉大学学报(信息科学版). 2024(04): 516-526 . 百度学术
3.	高昊，王仁茂. 基于类脑仿生的环境感知技术. 舰船电子对抗. 2024(05): 42-46+55 . 百度学术
4.	陈荟慧，钟委钊. 基于人机协作的高质量城市图像采集方法. 应用科学学报. 2023(05): 801-814 . 百度学术
5.	朱祥维，沈丹，肖凯，马岳鑫，廖祥，古富强，余芳文，高柯夫，刘经南. 类脑导航的机理、算法、实现与展望. 航空学报. 2023(19): 6-38 . 百度学术
6.	于乃功，廖诣深. 基于鼠脑内嗅—海马认知机制的移动机器人空间定位模型. 生物医学工程学杂志. 2022(02): 217-227 . 百度学术
7.	刘溢，阳加远，张驰. 一种基于RTX的移动机器人实时控制平台. 电子技术与软件工程. 2022(08): 169-172 . 百度学术
8.	于子航，王改云. 基于路径积分强化的机器人目标导向运动控制. 计算机仿真. 2022(07): 412-415+516 . 百度学术
9.	董卫华，刘毅龙，黑巧松，杨天宇. 泛地图空间认知理论与方法研究框架. 武汉大学学报(信息科学版). 2022(12): 2007-2014 . 百度学术
10.	阮晓钢，李鹏，朱晓庆，刘鹏飞. 基于目标导向行为和空间拓扑记忆的视觉导航方法. 计算机学报. 2021(03): 594-608 . 百度学术
11.	赵辰豪，吴德伟，韩昆，代传金. 无环境信息下多尺度网格细胞群空间表征模型. 系统工程与电子技术. 2021(03): 814-822 . 百度学术
12.	阮晓钢，柴洁，武悦，张晓平，黄静. 基于海马体位置细胞的认知地图构建与导航. 自动化学报. 2021(03): 666-677 . 本站查看
13.	冀俊忠，刘金铎，邹爱笑，杨翠翠. 一种融合多源信息的脑效应连接网络蚁群学习算法. 自动化学报. 2021(04): 864-881 . 本站查看
14.	万刚，武易天. 地图空间认知的数学基础. 测绘学报. 2021(06): 726-738 . 百度学术
15.	洪涛，史涛，任红格. 一种改进型RatSLAM算法构建认知地图的研究. 现代计算机. 2021(21): 47-52 . 百度学术
16.	韩昆，吴德伟，来磊. 类脑导航中基于差分Hebbian学习的网格细胞构建模型. 系统工程与电子技术. 2020(03): 674-679 . 百度学术
17.	黄宜庆，王正刚，王徽，葛愿. 基于边缘梯度算法的多移动机器人协作地图构建. 信息与控制. 2020(01): 62-68 . 百度学术
18.	于乃功，廖诣深，郑相国. 一种基于海马位置细胞选择机制的空间认知模型. 生物医学工程学杂志. 2020(01): 27-37 . 百度学术
19.	胡小平，毛军，范晨，张礼廉，何晓峰，韩国良，范颖. 仿生导航技术综述. 导航定位与授时. 2020(04): 1-10 . 百度学术
20.	于乃功，冯慧，廖诣深，郑相国. 一种基于感知速度与感知角度的网格野计算模型. 生物医学工程学杂志. 2020(05): 863-874 . 百度学术
21.	晁丽君，熊智，杨闯，华冰，王雅婷，刘建业. 无人飞行器三维类脑SLAM自主导航方法. 飞控与探测. 2020(05): 35-43 . 百度学术
22.	张孝伍. 图上的概率分布及位置方向信息的表征方法. 青岛理工大学学报. 2019(01): 113-121 . 百度学术
23.	方略，何洪军. 基于鼠脑海马位置细胞与Q学习面向目标导航. 生物信息学. 2019(01): 31-38 . 百度学术
24.	王均，凌有铸，王静. 基于特征融合的仿生SLAM算法研究. 安徽工程大学学报. 2019(02): 26-33 . 百度学术
25.	刘建业，杨闯，熊智，赖际舟，熊骏. 无人机类脑吸引子神经网络导航技术. 导航定位与授时. 2019(05): 52-60 . 百度学术
26.	韩昆，吴德伟，来磊，杨林. 自主导航条件下网格细胞放电模型. 电子科技大学学报. 2019(05): 711-716 . 百度学术
27.	丛明，邹强，刘冬，杜宇. 定位细胞认知机理启发的机器人导航研究综述. 机械工程学报. 2019(23): 1-12 . 百度学术
28.	邹强，丛明，刘冬，杜宇. 仿鼠脑海马的机器人地图构建与路径规划方法. 华中科技大学学报(自然科学版). 2018(12): 83-88 . 百度学术
29.	吴德伟，何晶，韩昆，李卉. 无人作战平台认知导航及其类脑实现思想. 空军工程大学学报(自然科学版). 2018(06): 33-38 . 百度学术

其他类型引用(29)

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

基于混合模糊多人多目标非合作博弈的车道选择模型

doi: 10.16383/j.aas.2017.c160559

通讯作者:
王晓原山东理工大学交通与车辆工程学院教授.主要研究方向为交通运输规划与管理, 交通信息工程及控制, 交通行为及安全, 交通流理论, 交通仿真和人车环境协同智慧及控制.本文通信作者.E-mail:wangxiaoyuan@sdut.edu.cn

计量

Drivers' Lane Choice Model Based on Mixed Fuzzy Multi-person and Multi-objective Non-cooperative Game

期刊类型引用(29)

其他类型引用(29)

计量

目录

留言板

基于混合模糊多人多目标非合作博弈的车道选择模型

doi: 10.16383/j.aas.2017.c160559

通讯作者: 王晓原 山东理工大学交通与车辆工程学院教授.主要研究方向为交通运输规划与管理, 交通信息工程及控制, 交通行为及安全, 交通流理论, 交通仿真和人车环境协同智慧及控制.本文通信作者.E-mail:wangxiaoyuan@sdut.edu.cn

计量

出版历程

Drivers' Lane Choice Model Based on Mixed Fuzzy Multi-person and Multi-objective Non-cooperative Game

期刊类型引用(29)

其他类型引用(29)

计量

出版历程

目录

通讯作者:
王晓原山东理工大学交通与车辆工程学院教授.主要研究方向为交通运输规划与管理, 交通信息工程及控制, 交通行为及安全, 交通流理论, 交通仿真和人车环境协同智慧及控制.本文通信作者.E-mail:wangxiaoyuan@sdut.edu.cn