Robust Exponential Almost Sure Stability of Discrete-time Two-level Switched Systems
-
摘要: 提出了一种新类型的切换系统——两层切换系统(Two-level switched systems, TSSs),其顶层切换是确定的,底层切换为随机的且由多个Markov链支配.基于持续驻留时间(Persistent dwell-time, PDT)方法,研究了TSS存在参数不确定性情况下的鲁棒指数几乎处处(Exponential almost sure, EAS)稳定性,以线性矩阵不等式(Linear matrix inequality, LMI)形式给出了一个充分条件.最后通过数值仿真例子验证了本文方法的有效性.
-
关键词:
- 两层切换系统 /
- 持续驻留时间 /
- 鲁棒指数几乎处处稳定 /
- 离散随机系统
Abstract: This paper proposes a new type of switched systems called two-level switched systems(TSSs). In a TSS, the top-level switching is deterministic, while the low-level switching is governed by multiple Markov chains and thus it is stochastic. Considering a TSS with parameter uncertainties, the robust exponential almost sure(EAS) stability is investigated. Based on the method of persistent dwell-time(PDT), a sufficient condition of robust EAS stability is given in the form of linear matrix inequalities(LMIs). A numerical example is provided to demonstrate the effectiveness of the proposed result. -
切换系统是一类特殊的混杂系统,由一族子系统和相应的切换规则构成.根据切换驱动机制的不同,切换系统可分为两类:确定性切换系统和随机切换系统.确定性切换系统表征了切换规则可控的切换系统,例如自动换挡的汽车、切换姿态的飞机追踪等. 驻留时间(Dwell time,DT)[1]和平均驻留时间(Average dwell-time,ADT)[2]方法是研究确定性切换系统稳定性的常见方法.近年来有学者提出利用持续驻留时间(Persistent dwell-time,PDT)方法研究切换系统的稳定性[3].PDT方法是按照各子系统驻留时间长短将切换序列按次序划分成快变部分( $T$ 部分)和缓变部分( $\tau$ 部分),并且分别对两部分的长度加以限制来保证整个切换系统的稳定性.相较于DT和ADT方法,PDT方法更具一般性,可以包含DT和ADT这两种约束情形[3].针对符合PDT约束的切换线性系统,文献[4]研究了 $H_{\infty}$ 滤波问题.
在随机切换系统中,马尔科夫跳变线性系统(Markov jump linear system,MJLS)是最为常见的一种类型,其子系统间的切换服从马尔科夫(Markov)过程,常用于描述系统结构或参数存在的随机突变[5-7].在过去十余年中,MJLS的稳定性问题得到了较充分的研究,主要涉及均方(Mean square,MS)稳定[8]、随机稳定性[9]、 $\delta $ 阶( $\delta$ -moment)稳定[10]和指数几乎处处(Exponential almost sure,EAS)稳定[11]等.
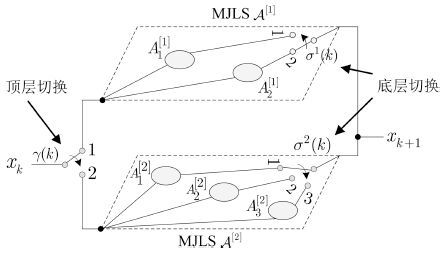
随着控制系统的复杂化,有学者进一步在切换机制或系统结构上加以变化,提出了若干新类型的切换系统[12-14].例如文献[12]研究了一种具有复合切换机制的切换系统,其子系统的驻留时间包括两部分:确定性部分和随机驻留时间(服从指数分布). 显然,若各子系统的确定性驻留时间为零,则上述切换系统就退化成MJLS.而文献[13 $-$ 14]考虑切换系统结构上的变化,提出了切换动态MJLS(Switching dynamics MJLS,SD-MJLS)[13]和切换MJLS (Switching MJLS,S-MJLS)[14]这两种新类型系统.SD-MJLS和S-MJLS结构如图 1所示,整个系统中同时存在着确定性切换 $\gamma (k)$ 和Markov切换 $\sigma(k)$ . 横向的确定性切换选择某个子系统激活工作,纵向Markov随机切换选择工作模态. SD-MJLS/S-MJLS不同之处在于,SD-MJLS中Markov链转移速率是固定不变的,即确定性切换不影响Markov链的转移速率.而S-MJLS中的Markov链转移速率会随着子系统的切换而变化.文献[14]研究了确定性切换满足DT约束时S-MJLS的MS稳定性,文献[13]分别针对确定性切换满足DT和ADT约束的情况,利用Markov链的遍历性研究了SD-MJLS的EAS稳定性.
在上述基础上,本文提出了另一种新结构类型的切换系统---两层切换系统(Two-level switched system,TSS),如图 2所示. 在TSS中,多个MJLS子系统间的切换(顶层切换)是确定性的,每个MJLS子系统模态间的随机切换(底层切换)则服从不同的Markov链.与SD-MJLS/S-MJLS相比,TSS更具一般性: 在SD-MJLS/S-MJLS中,不同MJLS子系统的模态数必须相同且由同一个Markov链控制模态切换;而在TSS中,不同MJLS子系统模态间的切换是由不同的Markov链控制,因而模态数目可以不同.SD-MJLS/S-MJLS可以视为本文TSS的一个特例(当TSS底层切换由同一个Markov链控制时).TSS可以用于具有复杂切换特性系统的建模,例如一个具有多个工作状况的复杂系统,其工况切换取决于确定性的控制指令,而不同的工况下系统中随机故障的类型可能各不相同,需采用不同的Markov链来描述. 此时该系统的数学模型就是一个TSS.
本文针对存在参数不确定性的TSS,研究了其鲁棒EAS稳定性.值得一提的是,由于TSS中多个MJLS交替作用,无法采用文献[13]中基于Markov链遍历性特征的研究方法.本文通过分析MJLS的随机统计特征并结合PDT方法,以线性矩阵不等式形式给出了TSS鲁棒EAS稳定的一个充分条件.仿真例子验证了结论的正确性.
符号说明: 在本文中, ${{1}_{N \times N}}$ 表示元素全为1的 $N\times N$ 维矩阵,上标 ${\rm T}$ 表示矩阵或向量转置, $\left\lceil a\right\rceil $ 表示不大于 $a$ 的最大整数, ${\lambda _{\max}}(M)$ 和 ${\lambda _{\min }}(M)$ 分别表示矩阵 $M$ 的最大特征值和最小特征值, ${\bf Z}{_ +}$ 表示非负整数集, ${\bf Z}{_{[{n_1},{n_2}]}}$ 表示集合 $\{ k \in{\bf Z}{_ + }|{n_1} \le k \le {n_2}\} $ .
1. 问题描述
考虑如下离散时间两层切换系统:
\begin{align}{{\mathit{\boldsymbol{x}}}_{k + 1}} = \bar A_{{\sigma ^{\gamma (k)}}(k)}^{[\gamma(k)]}{{\mathit{\boldsymbol{x}}}_k}\end{align}
(1) 其中系统状态 ${{\mathit{\boldsymbol{x}}}_k} \in {\bf R}{^n}$ ,顶层切换 $\gamma (k) \in{\cal M}: = \{ 1,2,\cdots,$ $M\}$ 是一个分段常值函数,指定一个子MJLS在 $k$ 时刻作用,底层切换 ${\sigma ^{\gamma (k)}}(k) \in{{\cal N}_{\gamma (k)}}: = \{ 1,2,\cdots,{N_{\gamma (k)}}\}$ 是一个Markov链,决定第 $\gamma (k)$ 个子MJLS的一个模态在 $k$ 时刻作用. $\bar A_i^{[j]} \in \{ A_i^{[j]} + L_i^{[j]}\Delta_i^{[j]}N_i^{[j]}|\Delta _i^{[j]} \in {\bf R}{^{m_i^{[j]} \times p_i^{[j]}}}, || {\Delta _i^{[j]}}|| \le w_i^{[j]}\}$ , $j \in{\cal M}$ , $i \in {{\cal N}_j}$ ,其中 $A_i^{[j]} \in {\bf R}{^{n\times n}}$ , $L_i^{[j]} \in {\bf R}{^{n \times m_i^{[j]}}}$ 和 $N_i^{[j]} \in {\bf R}{^{p_i^{[j]} \times n}}$ 是常数矩阵, $w_i^{[j]}$ 是给定的扰动半径.
$\forall j \in {\cal M}$ ,Markov链 $\{ {\sigma ^j}(k)\}$ 的一步转移概率矩阵记为 ${P^{[j]}}: = {[p_{rs}^{[j]}]_{{N_j} \times{N_j}}}$ , $p_{rs}^{[j]}: = Pr \{ {\sigma ^j}(k + 1) = s|{\sigma^j}(k) = r\} $ , $r, s \in {{\cal N}_j}$ ;两层切换系统(1) 顶层切换的初始位置记为 ${\gamma _0}: = \gamma (0) $ ,对应的子MJLS的初始概率分布记为 ${{f}^{{\gamma _0}}} = [f_1^{{\gamma_0}} f_2^{{\gamma _0}} \cdots f_{{N_{{\gamma _0}}}}^{{\gamma_0}}]$ ,其中 $f_i^{{\gamma _0}} = Pr \{ {\sigma ^{{\gamma _0}}}(0) = i\} $ , $ i \in {{\cal N}_{{\gamma _0}}}$ . $\forall j \in {\cal M}$ ,本文假设Markov链 $\{ {\sigma ^j}(k)\} $ 是不可约且非周期的,则它是遍历的且存在平稳分布 ${{\pi} ^{[j]}} = [\pi _1^{[j]} \pi_2^{[j]} \cdots \pi _{{N_j}}^{[j]}]$ ,满足方程 ${{\pi}^{[j]}} = {{\pi}^{[j]}}{P^{[j]}}$ 和 $\sum\nolimits_{i = 1}^{{N_j}}{\pi _i^{[j]}} = 1$ .
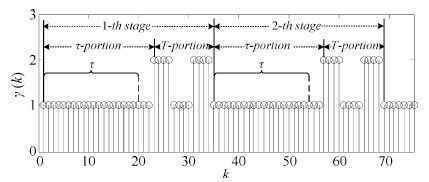
如图 3所示,PDT切换是由切换规则相同的阶段构成,每个阶段均包括两个部分: $\tau $ 部分和 $T$ 部分. 在 $\tau $ 部分中,只有一个子系统(该子系统可以是任意的一个,并非为固定)激活且其作用时间至少为 $\tau $ ; 在 $T$ 部分中,有多个子系统激活,每个子系统的作用时间小于 $\tau$ 且所有激活子系统作用的总时间小于 $T$ .如果第 $p$ 阶段中 $T$ 部分的实际运行时间记为 ${T_p}$ ,则 ${T_p} =\sum\nolimits_{r = 1}^{{\theta _p}} {{T^{[\gamma ({k_{{s_{_{p}}} +r}})]}}} \le T$ ,其中 ${T^{[\gamma ({k_{{s_{_{p}}} + r}})]}} <\tau $ 表示在切换时刻 ${k_{{s_{_{p}}} + r}} \in [{k_{{s_{_{p}}} +1}},{k_{{s_{_{p + 1}}}}}), r \in {\bf Z}{_{[1,{\theta_p}]}}$ 处激活子系统的运行时间, ${\theta _p}: = \theta({k_{{s_{_{p}}} + 1}},{k_{{s_{_{p + 1}}}}})$ 表示 $\gamma(k)$ 在区间 $[{k_{{s_{_{p}}} + 1}},{k_{{s_{_{p +1}}}}})$ 内的切换次数, ${k_{{s_{_{p}}} +1}}$ 表示第 $p$ 个阶段中时刻 ${k_{{s_p}}}$ 之后的下一个切换时刻, ${k_{{s_{_{p + 1}}}}}$ 表示第 $p + 1$ 阶段的切入时刻.
本文研究了顶层切换满足PDT约束,且存在参数不确定性的TSS鲁棒EAS稳定性问题,下面给出了相关定义:
定义1[3]. 考虑切换时刻 ${k_0},{k_1},\cdots,{k_s},\cdots $ ,其中 ${k_0} = 0$ .假如存在无数个长度大于 $\tau $ 的不相交区间,且具有该性质的连续区间被一个不大于 $T$ 的时间间隔分割,则常数 $\tau> 0$ 被称为持续驻留时间(Persistent dwell-time,PDT), $T$ 被称为持续周期.
定义2[15]. 对于切换信号 $\sigma$ 和任意给定的时刻 $K \ge k \ge {k_0}$ ,记 ${N_\sigma}(k,K)$ 为 $\sigma $ 在 $[k,K)$ 内的切换次数. 如果对于 ${\tau _a} > 0$ , ${N_0} > 0$ ,满足 ${{N}_{\sigma }}(k,K)\le {{N}_{0}}+(K-k)(K-k){{\tau }_{a}}$ ,则 ${\tau _a}$ 是切换信号 $\sigma $ 的平均驻留时间, ${N_0}$ 称为抖振界.
注1. 由PDT切换的定义可知,当 ${T=0}$ 时,PDT切换将退化为DT切换. 另一方面,如果用 ${\vartheta _{ADT}}({\tau_a},{N_0})$ 表示参数为 ${\tau _a}$ 和 ${N_0}$ 的ADT切换的集合,用 ${\vartheta _{PDT}}(\tau ,T)$ 表示参数为 $\tau$ 和 $T$ 的PDT切换的集合. 则任意满足ADT切换 ${\vartheta _{ADT}}({\tau_a},{N_0})$ 的切换信号所等效的PDT切换为 ${\vartheta _{PDT}}(\delta{\tau _a},\eta {\tau _a})$ ,其中 ${\tau _a} > 0$ , ${N_0} \ge 1$ , $\delta \in (0,1) $ 和 $\eta=$ $\delta ({{N}_{0}}-1)\delta ({{N}_{0}}-1)(1-\delta )$ . 详细推导可参见文献[3].
定义3[16]. 对于任意初始条件( ${{\mathit{\boldsymbol{x}}}_0},{\gamma _0},{{f}^{{\gamma _0}}}$ ) 和 $\forall \Delta _i^{[j]}$ 满足 $ || {\Delta _i^{[j]}} || \le w_i^{[j]}$ ,离散时间不确定TSS (1) 是鲁棒EAS 稳定的当且仅当 $\exists \rho >0$ ,有下面等式成立
\begin{align}Pr \left. {\left\{ {\mathop {\lim }\limits_{k \to \infty } \sup\frac{1}{k}\ln || {{\mathit{\boldsymbol{x}}}_k} || \le - \rho } \right.} \right\}= 1\end{align}
(2) 引理1[17]. 对于任意初始条件( ${{\mathit{\boldsymbol{x}}}_0},{\gamma _0},{{f}^{{\gamma _0}}}$ ) 和 $ \forall \Delta _i^{[j]}$ 满足 $ || {\Delta _i^{[j]}} || \le w_i^{[j]}$ ,离散时间不确定TSS (1) 是鲁棒EAS 稳定的当且仅当 ${\rm E}(\lambda )<0$ ,其中 $\lambda $ 是最大李亚普诺夫指数定义为
\begin{align}\lambda = \mathop {\lim }\limits_{k \to \infty } \sup\frac{1}{k}\ln || {\Phi (0,k)} ||\end{align}
(3) $\Phi (0,k)$ 是两层切换系统(1) 的随机转移矩阵.
注2. 本文的两层切换系统(1) 是由多个不同的MJLS子系统组成,不同的MJLS子系统模态间的切换是由不同的Markov链控制.对于(1) 中任意的子系统,每次切入时子系统模态的选取是任意的,和上次该子系统切出时的模态之间不存在Markov跳变关系,因此该子系统所对应的Markov链是不连续的且无法达到稳定状态,这将无法仿照文献[13]利用Markov链的遍历性来简化EAS稳定性分析. 为此,必须对Markov链进行暂态分析. 下面给出了Markov 链的两个暂态特性.
引理2[11]. 考虑一个 $N$ 模态的Markov 链 $\{\sigma (k)\}$ ,记 ${T_i}(0,k)$ 为模态 $i$ 在区间 $[0,k)$ 内总的作用时间(即驻留时间), ${N_{ij}}(0,k)$ 为区间 $[0,k)$ 内由模态 $i$ 跳转到模态 $j$ 的总次数.则在初始概率分布 ${f} = [{f_1} \cdots {f_{N}}]$ 已知时,对于所有的模态 $i,~j$ 有下面的等式成立
\begin{align}&{\rm E}[{T_i}(0,k)] = {\pi _i}k + ( {f} - {\pi} ){\left[{\sum\limits_{j = 1}^k {{P^j}} } \right]_i}\end{align}
(4) \begin{align}&{\rm E}[{N_{ij}}(0,k)]= {\pi _i}{p_{ij}}k + {p_{ij}}( {f} - {\pi} ){\left[{\sum\limits_{j = 1}^k {{P^j}} } \right]_i} + \nonumber\\&\quad ({f_i} - {\pi _i}){p_{ij}},i \ne j\end{align}
(5) 其中 ${[\cdot]_i}$ 表示一个矩阵的第 $i$ 列, $P={[p_{ij}]_{N \times N}}$ 为Markov链 $\{\sigma (k)\}$ 的转移概率矩阵, ${\pi} = [{\pi _1}\cdots {\pi _N}]$ 为其平稳分布.
注3. 引理2给出了Markov链 $\{\sigma(k)\}$ 的两个暂态特性. 可以看出 ${\rm E}[{T_i}(0,k)]$ 和 ${\rm E}[{N_{ij}}(0,k)]$ 与初始概率分布 ${f}$ 是有关的.当 ${f}$ 为任意或未知时, ${\rm E}[{T_i}(0,k)]$ 和 ${\rm E}[{N_{ij}}(0,k)]$ 的取值范围有如下关系,证明见附录A.
\begin{align}&{\pi _i}k - {\delta _i} \le {\rm E}[{T_i}(0,k)] \le {\pi _i}k +{\delta _i}\end{align}
(6) \begin{align}&{\pi _i}{p_{ij}}k - {p_{ij}}{\delta _i} - {\pi _i}{p_{ij}}\le {\rm E}[{N_{ij}}(0,k)]\le {\pi _i}{p_{ij}}k +\nonumber\\&\quad {p_{ij}}{\delta _i} + {p_{ij}} - {\pi _i}{p_{ij}},i \ne j\end{align}
(7) 其中, ${\delta _i}$ 为 $( {f} - {\pi} ){\left[{\sum\nolimits_{j =1}^k {{P^j}} } \right]_i}$ 的最大值,计算方法见附录A.
2. 主要结果
基于注3中Markov链暂态特性的取值范围和PDT方法,下面给出了不确定TSS(1) 鲁棒EAS稳定的一个充分条件.
定理 1. 考虑离散时间不确定TSS (1) ,对于 $\forall i,j\in {\cal M}$ ,若存在一组矩阵 $Q_r^{[j]} > 0$ 以及标量 $\xi _{}^{[i]} >1$ 、 $s_r^{[j]} > 0$ 、 $\lambda _r^{[j]} > 0$ ,满足式(8) $\sim$ (11) ,PDT切换参数满足式(12) ,则切换系统是鲁棒EAS稳定的.
\begin{align}&\qquad Q_q^{[j]} \le \xi _{}^{[i]}Q_r^{[i]}, i \ne j, q\in{{\cal N}_i},{\rm{ }}r \in {{\cal N}_j}\end{align}
(8) \begin{align}&\qquad \quad {(L_r^{[j]})^{\rm T}}Q_r^{[j]}L_r^{[j]} \le s_r^{[j]}I,{\rm{}}r \in {{\cal N}_j}\end{align}
(9) \begin{align}& \left[{\begin{array}{*{20}{c}}{B_r^{[j]}}&{D_r^{[j]}}&{{{(N_r^{[j]})}^{\rm T}}}\\{{{(D_r^{[j]})}^{\rm T}}}&{\frac{{ - 1}}{{{{(w_r^{[j]})}^2}}}I}&0\\{N_r^{[j]}}&0&{\frac{{ - 1}}{{1 + s_r^{[j]}{{(w_r^{[j]})}^2}}}I}\end{array}} \right] \le 0,r \in {{\cal N}_j}\end{align}
(10) \begin{align}&\qquad Q_r^{[j]} \le u_{qr}^{[j]}Q_q^{[j]}, q, r \in{{\cal N}_j}, q \ne r\end{align}
(11) \begin{align}&\qquad \qquad \frac{{\tilde \beta (T + 1) }}{{\tau + T}} + \tilde\alpha<0\end{align}
(12) 其中,$B_r^{[j]} = {(A_r^{[j]})^{\rm T}}Q_r^{[j]}A_r^{[j]} -\lambda _r^{[j]}Q_r^{[j]}$,$D_r^{[j]} = $ ${(A_r^{[j]})^{\rm T}}Q_r^{[j]}L_r^{[j]}$,$\tilde \alpha = {\max _{j \in {\cal M}}}\{ {\alpha ^{[j]}}\} <0$,$\tilde \beta = $ ${\max _{j \in{\cal M}}}\{ {\beta ^{[j]}}\} $,${\alpha ^{[j]}} =$ $\sum\nolimits_{a = 1}^{{N_j}} {\pi _a^{[j]}\ln \lambda _a^{[j]} +} $ $\sum\nolimits_{\begin{matrix} b=1,a=1\text{ } \\ a\ne b \\ \end{matrix}}^{{{N}_{j}}}{p_{ba}^{[j]}\pi _{b}^{[j]}\ln u_{ba}^{[j]}}$,${\beta ^{[j]}} = \ln {\xi ^{[j]}} +\sum\nolimits_{a \in {\cal N}_j^{{\lambda ^ + }}} {\delta_a^{[j]}} \ln \lambda _a^{[j]} - \sum\nolimits_{a \in {\cal N}_j^{{\lambda ^ - }}} {\delta _a^{[j]}\ln \lambda _a^{[j]}} +\sum\nolimits_{(b,a) \in {\cal N}_j^{{u^ + }}}{(p_{ba}^{[j]}\delta _b^{[j]}}- $ $\pi _b^{[j]}p_{ba}^{[j]} +p_{ba}^{[j]})\ln u_{ba}^{[j]} - \sum\nolimits_{(b,a) \in {\cal N}_j^{{u^ - }}} {(p_{ba}^{[j]}\delta _b^{[j]} + \pi_b^{[j]}p_{ba}^{[j]})\ln u_{ba}^{[j]}} $,${\cal N}_j^{{\mu ^ + }}= \{ (m,n) | \mu _{mn}^{[j]} \ge 1, m,n \in {{\cal N}_j} ,m\ne n \}$,${\cal N}_j^{{\mu ^ - }} = \{ (m,n) | \mu_{mn}^{[j]}<1, m,n \in {{\cal N}_j} ,m \ne n \} $,${\cal N}_j^{{\lambda ^ + }} = \{ m \in {{\cal N}_j} | \lambda_m^{[j]} > 1\} $,${\cal N}_j^{{\lambda ^ - }} = \{ m \in {{\cal N}_j} | \lambda _m^{[j]}<1\} $,$\delta_b^{[j]}$由附录A可得.
证明 .构造一个分段李雅普诺夫函数 $V(k) = {\mathit{\boldsymbol{x}}}_k^{\rm T}Q_{N(k)}^{[\gamma (k)]}{{\mathit{\boldsymbol{x}}}_k}$ ,其中 $N(k) = {\sigma ^{\gamma(k)}}(k)$ . 为了便于分析,假设顶层切换 $\gamma(k)$ 在第 $p$ 阶段内发生了 $n$ 次切换,对应的切换时刻由小到大依次为 ${h_1}$ , ${h_2}$ , $\cdots$ , ${h_n}$ ,如图 4所示. 其中, ${h_1}$ 为第 $p$ 阶段的切入时刻, $\bar h$ 为第 $p +1$ 阶段的切入时刻.
考虑如下一个顶层切换序列:
$\left\{ \begin{array}{l}\gamma (k) = j, k \in [{h_n},\bar h),\\\gamma (\bar h) = i,\end{array} \right. i \ne j$
并假定 $ {\sigma ^i}(\bar h) = m,m \in {{\cal N}_i}$ .
不失一般性,假设在区间 $[{h_n},\bar h) $ 内底层切换的次数为 $l$ ,其对应的切换时刻由小到大依次记为 ${s_1} ({s_1} = {h_n}),{s_2},\cdots , {s_l}$ . 因此,
$\begin{array}{l}{\sigma ^j}({s_1}) = {\sigma ^j}({s_1} + 1) = \cdots = {\sigma ^j}({s_2} - 1) \ne \\\quad{\sigma ^j}({s_2}) \cdots\ne {\sigma ^j}({s_{l - 1}}) = b = \cdots = {\sigma ^j}({s_l} - 1) \ne \\\quad {\sigma ^j}({s_l})= a = \cdots ={\sigma ^j}(\bar h - 1) \end{array}$
根据条件(8) 以及式(1) ,可得
\begin{align}&V(\bar h)= {\mathit{\boldsymbol{x}}}_{\bar h}^{\rm T}Q_m^{[i]}{{\mathit{\boldsymbol{x}}}_{\bar h}}\le\nonumber\\&{\xi ^{[j]}}{\mathit{\boldsymbol{x}}}_{\bar h}^{\rm T}Q_a^{[j]}{{\mathit{\boldsymbol{x}}}_{\bar h}}=\nonumber\\&{\xi ^{[j]}}{\mathit{\boldsymbol{x}}}_{\bar h - 1}^{\rm T}\left( {{{(A_a^{[j]})}^{\rm T}}Q_a^{[j]}A_a^{[j]} + } \right.\nonumber\\&{{(A_a^{[j]})}^{\rm T}}Q_a^{[j]}L_a^{[j]}\Delta _a^{[j]}N_a^{[j]} + {(L_a^{[j]}\Delta _a^{[j]}N_a^{[j]})^{\rm T}}Q_a^{[j]}A_a^{[j]}+\nonumber\\&\left. { {{(N_a^{[j]})}^{\rm T}}{{(\Delta _a^{[j]})}^{\rm T}}{{(L_a^{[j]})}^{\rm T}}Q_a^{[j]}L_a^{[j]}\Delta _a^{[j]}N_a^{[j]}} \right){{\mathit{\boldsymbol{x}}}_{\bar h - 1}}=\nonumber\\&{\xi ^{[j]}}{\mathit{\boldsymbol{x}}}_{\bar h - 1}^{\rm T}\left( {E_a^{[j]} + F_a^{[j]}G_a^{[j]} + {{(F_a^{[j]}G_a^{[j]})}^{\rm T}}} \right.+\nonumber\\&\left. { {{(G_a^{[j]})}^{\rm T}}{{(L_a^{[j]})}^{\rm T}}Q_a^{[j]}L_a^{[j]}G_a^{[j]}} \right){{\mathit{\boldsymbol{x}}}_{\bar h -1}}\end{align}
(13) 其中 $E_a^{[j]} = {(A_a^{[j]})^{\rm T}}Q_a^{[j]}A_a^{[j]}$ , $F_a^{[j]} = {(A_a^{[j]})^{\rm T}}Q_a^{[j]}L_a^{[j]}$ , $G_a^{[j]}= \Delta _a^{[j]}N_a^{[j]}$ . 由条件(9) 知 ${(L_a^{[j]})^{\rm T}}Q_a^{[j]}L_a^{[j]} \le s_a^{[j]}I$ ,则
\begin{align}&E_a^{[j]} + F_a^{[j]}G_a^{[j]} + {(F_a^{[j]}G_a^{[j]})^{\rm T}}+\notag\\&\quad {(G_a^{[j]})^{\rm T}}{(L_a^{[j]})^{\rm T}}Q_a^{[j]}L_a^{[j]}G_a^{[j]}\le\notag\\&\quad E_a^{[j]} + F_a^{[j]}G_a^{[j]} +{(F_a^{[j]}G_a^{[j]})^{\rm T}} + s_a^{[j]}{(G_a^{[j]})^{\rm T}}G_a^{[j]}=\notag\\&\quad E_a^{[j]} - \left( {w_a^{[j]}F_a^{[j]} -\frac{{{{(G_a^{[j]})}^{\rm T}}}}{{w_a^{[j]}}}} \right)\times\notag\\&\quad {\left( {w_a^{[j]}F_a^{[j]} - \frac{{{{(G_a^{[j]})}^{\rm T}}}}{{w_a^{[j]}}}} \right)^{\rm T}}+{(w_a^{[j]})^2} F_a^{[j]}{(F_a^{[j]})^{\rm T}}+\notag\\&\quad \left(\frac{1}{(w_a^{[j]})^2 }+s_a^{[j]}\right){(G_a^{[j]})^{\rm T}}G_a^{[j]}\le\notag\\&\quad E_a^{[j]} + {(w_a^{[j]})^2} F_a^{[j]}{(F_a^{[j]})^{\rm T}}+\notag\\&\quad \left(\frac{1}{(w_a^{[j]})^2 }+s_a^{[j]}\right){(G_a^{[j]})^{\rm T}}G_a^{[j]}\end{align}
(14) 又因为 $|| {\Delta _a^{[j]}} || \le w_a^{[j]}$ , $\frac{{{{(\Delta_a^{[j]})}^{\rm T}}\Delta _a^{[j]}}}{{{{(w_a^{[j]})}^2}}} \le I$ ,所以
\begin{align}&\left(\frac{1}{(w_a^{[j]})^2 }+ s_a^{[j]}\right){(G_a^{[j]})^{\rm T}}G_a^{[j]}\le\nonumber\\&\quad (1 + s_a^{[j]}{(w_a^{[j]})^2}){(N_a^{[j]})^{\rm T}}N_a^{[j]}\end{align}
(15) 将式(15) 代入式(14) ,并结合式(13) 得
\begin{align}V(\bar h) &\le {\xi ^{[j]}}{\mathit{\boldsymbol{x}}}_{\bar h - 1}^{\rm T}\left( {E_a^{[j]} + {{(w_a^{[j]})}^2} F_a^{[j]}{{(F_a^{[j]})}^{\rm T}}} \right.+\nonumber\\&\quad \left. { ( {1 + s_a^{[j]}{{(w_a^{[j]})}^2}}){{(N_a^{[j]})}^{\rm T}}N_a^{[j]}} \right){{\mathit{\boldsymbol{x}}}_{\bar h -1}}\end{align}
(16) 由Schur补引理,条件(10) 等价于
\begin{align}&E_a^{[j]} + {(w_a^{[j]})^2} F_a^{[j]}{(F_a^{[j]})^{\rm T}}+ \nonumber\\&\quad (1 + s_a^{[j]}{(w_a^{[j]})^2}){(N_a^{[j]})^{\rm T}}N_a^{[j]}\le \lambda _a^{[j]}Q_a^{[j]}\end{align}
(17) 将式(17) 代入到式(16) 可得
\begin{align}V(\bar h) \le {\xi ^{[j]}}\lambda _a^{[j]}{\mathit{\boldsymbol{x}}}_{\bar h -1}^{\rm T}Q_a^{[j]}{{\mathit{\boldsymbol{x}}}_{\bar h - 1}}\end{align}
(18) 注意到在区间 $[{s_l},\bar h - 1]$ 上只有第 $j$ 个MJLS的模态 $a$ 作用,用式(13) $\sim$ (18) 类似的推导可得
\begin{align}V(\bar h) &\le {\xi ^{[j]}}\lambda _a^{[j]}{\mathit{\boldsymbol{x}}}_{\bar h - 1}^{\rm T}Q_a^{[j]}{{\mathit{\boldsymbol{x}}}_{\bar h - 1}}\le\nonumber\\&\quad {\xi ^{[j]}}{(\lambda _a^{[j]})^2}{\mathit{\boldsymbol{x}}}_{\bar h - 2}^{\rm T}Q_a^{[j]}{{\mathit{\boldsymbol{x}}}_{\bar h - 2}}\le\cdots\le\notag\\&\quad {\xi ^{[j]}}{(\lambda _a^{[j]})^{\bar h - {s_{_l}}}}{\mathit{\boldsymbol{x}}}_{{s_{_l}}}^{\rm T}Q_a^{[j]}{{\mathit{\boldsymbol{x}}}_{{s_{_l}}}}\end{align}
(19) 根据式(19) 和条件(11) ,可得
\begin{align}&V(\bar h)\le\nonumber\\&\quad {\xi ^{[j]}}{(\lambda _a^{[j]})^{\bar h - {s_{_l}}}}u_{ba}^{[j]}{\mathit{\boldsymbol{x}}}_{{s_{_l}}}^{\rm T}Q_b^{[j]}{{\mathit{\boldsymbol{x}}}_{{s_{_l}}}}=\nonumber\\&\quad {\xi ^{[j]}}{(\lambda _a^{[j]})^{\bar h -{s_{_l}}}}u_{ba}^{[j]}{\mathit{\boldsymbol{x}}}_{{s_{_l}} - 1}^{\rm T}{(\bar A_{b}^{[j]})^{\rm T}}Q_b^{[j]}\bar A_{ b}^{[j]}{{\mathit{\boldsymbol{x}}}_{{s_{_l}} -1}}\end{align}
(20) 由推导式(19) 和式(20) 类似的步骤可得
$\begin{align} & V(\bar{h})\le {{\xi }^{[j]}}{{(\lambda _{a}^{[j]})}^{\bar{h}-{{s}_{l}}}}u_{ba}^{[j]}\lambda _{b}^{[j]}\mathrm{x}_{{{s}_{l}}-1}^{T}\text{T}Q_{b}^{[j]}\mathrm{x}_{{{s}_{l}}-1}^{{}}\le \\ & {{\xi }^{[j]}}{{(\lambda _{a}^{[j]})}^{\bar{h}-{{s}_{l}}}}{{(\lambda _{b}^{[j]})}^{{{s}_{l}}-{{s}_{l}}-1}}u_{ba}^{[j]}\mathrm{x}_{{{s}_{l}}-1}^{T}Q_{b}^{[j]}\mathrm{x}_{{{s}_{l}}-1}^{{}}\le \cdots \le \\ & {{\xi }^{[j]}}\prod\limits_{a=1}^{{{N}_{j}}}{{}}{{(\lambda _{a}^{[j]})}^{T_{a}^{\left[ j \right]}({{s}_{1}},\bar{h})}}\times \\ & \prod\limits_{\begin{matrix} b=1,a=1 \\ a\ne b \\ \end{matrix}}^{{{N}_{j}}}{{}}{{(u_{ba}^{[j]})}^{N_{ba}^{[j]}({{s}_{1}},\bar{h})}}V({{s}_{1}}) \\ \end{align}$
(21) 其中 $T_a^{[j]}({s_1},\bar h)$ 表示第 $j$ 个子MJLS的模态 $a$ 在区间 $[{s_1},\bar h)$ 内的总驻留时间, $N_{ba}^{[j]}({s_1},\bar h)$ 表示在区间 $[{s_1},\bar h)$ 内第 $j$ 个子MJLS的模态由 $b$ 切换到 $a$ 的次数, ${s_1} = {h_n}$ .
式(21) 两边取对数可得
$\begin{align} & \ln V(\bar{h})\le \ln {{\xi }^{[j]}}+\sum\limits_{a=1}^{{{N}_{j}}}{T_{a}^{\left[ j \right]}({{h}_{n}},\bar{h})\ln \lambda _{a}^{[j]}}+ \\ & \quad \sum\limits_{\begin{matrix} b=1,a=1 \\ a\ne b \\ \end{matrix}}^{{{N}_{j}}}{N_{ba}^{[j]}({{h}_{n}},\bar{h})\ln u_{ba}^{[j]}}+\ln V({{h}_{n}}) \\ \end{align}$
(22) 则
\begin{align}&{\rm E}\left[{\ln V(\bar h)} \right] \le \ln {\xi ^{[j]}} \!\!+\!\! \sum\limits_{a \in {\cal N}_j^{{\lambda ^ + }} } {{\rm E}\left[{T_a^{\left[j \right]}({h_n},\bar h)} \right]\ln \lambda _a^{[j]}} +\nonumber\\&\quad \sum\limits_{a \in {\cal N}_j^{{\lambda ^ - }} } {{\rm E}\left[{T_a^{\left[j \right]}({h_n},\bar h)} \right]\ln \lambda _a^{[j]}} +\nonumber\\&\quad \sum\limits_{(b,a) \in {\cal N}_j^{{u^ + }}} {{\rm E}\left[{N_{ba}^{[j]}({h_n},\bar h)} \right]\ln u_{ba}^{[j]}}+ \nonumber\\&\quad \sum\limits_{(b,a) \in {\cal N}_j^{{u^ - }}} {{\rm E}\left[{N_{ba}^{[j]}({h_n},\bar h)} \right]\ln u_{ba}^{[j]}} +\nonumber\\&\quad {\rm E}\left[{\ln V({h_n})} \right]\end{align}
(23) 另一方面,由式(6) 和式(7) 可得
\begin{align}&\pi _a^{[j]}{\Delta _k} - \delta _a^{[j]} \le {\rm E}\left[{T_a^{[j]}({h_n},\bar h)} \right] \le \pi _a^{[j]}{\Delta _k} +\delta _a^{[j]}\end{align}
(24) \begin{align}&\pi _b^{[j]}p_{ba}^{[j]}{\Delta _k} - p_{ba}^{[j]}\delta _b^{[j]} - \pi _b^{[j]}p_{ba}^{[j]} \le {\rm E}\left[{N_{ba}^{[j]}({h_n},\bar h)} \right] \le \nonumber\\&~~\pi _b^{[j]}p_{ba}^{[j]}{\Delta _k} + p_{ba}^{[j]}\delta _b^{[j]}+ p_{ba}^{[j]} - \pi _b^{[j]}p_{ba}^{[j]}, b \ne a\end{align}
(25) 其中 ${\Delta _k} = \bar h - {h_n}$ . 将式(24) 和式(25) 代入式(23) ,可得
\begin{align}&\!\!\!\!{\rm E}\left[{\ln V(\bar h)} \right] \le \ln {\xi ^{[j]}}+\!\! \sum\limits_{a \in {\cal N}_j^{{\lambda ^ + }} } {(\pi_a^{[j]}{\Delta _k} + \delta _a^{[j]})\ln \lambda _a^{[j]}}+\notag\\&\sum\limits_{a \in {\cal N}_j^{{\lambda ^ - }} } {(\pi _a^{[j]}{\Delta _k} - \delta _a^{[j]})\ln \lambda _a^{[j]}}+ \!\!\!\!\sum\limits_{(b,a) \in {\cal N}_j^{{u^ + }}}(\pi _b^{[j]}p_{ba}^{[j]}{\Delta _k}+ \nonumber\\&{p_{ba}^{[j]}\delta _b^{[j]} + p_{ba}^{[j]} - \pi _b^{[j]}p_{ba}^{[j]})\ln u_{ba}^{[j]}}+\nonumber\\&\sum\limits_{(b,a) \in {\cal N}_j^{{u^ - }}} {(\pi _b^{[j]}p_{ba}^{[j]}{\Delta _k} - p_{ba}^{[j]}\delta _b^{[j]} - \pi _b^{[j]}p_{ba}^{[j]})\ln u_{ba}^{[j]}}+\nonumber\\&{\rm E}\left[{\ln V({h_n})} \right]={\beta ^{[j]}} + {\alpha^{[j]}}{\Delta _k} + {\rm E}\left[{\ln V({h_n})} \right] \end{align}
(26) 其中$\begin{align} & \quad \sum\limits_{\begin{matrix} b=1,a=1 \\ a\ne b \\ \end{matrix}}^{{{N}_{j}}}{N_{ba}^{[j]}({{h}_{n}},\bar{h})\ln u_{ba}^{[j]}}+\ln V({{h}_{n}}) \\ & {{\alpha }^{[j]}}=\sum\nolimits_{a=1}^{{{N}_{j}}}{\pi _{a}^{[j]}\ln \lambda _{a}^{[j]}+}\sum\nolimits_{\begin{matrix} b=1,a=1 \\ a\ne b\text{ }\!\!\backslash\!\!\text{ hfill} \\ \end{matrix}}^{{{N}_{j}}}{p_{ba}^{[j]}\pi _{b}^{[j]}\ln u_{ba}^{[j]}} \\ \end{align}$,${\beta ^{[j]}} = \ln {\xi ^{[j]}} + \sum\nolimits_{a \in {\cal N}_j^{{\lambda ^ + }}} {\delta _a^{[j]}\ln \lambda _a^{[j]}} - \sum\nolimits_{a \in {\cal N}_j^{{\lambda ^ - }}} {\delta _a^{[j]}} \times $ $\ln \lambda _a^{[j]} + \sum\nolimits_{(b,a) \in {\cal N}_j^{{u^ + }}} {(p_{ba}^{[j]}\delta _b^{[j]} - \pi _b^{[j]}p_{ba}^{[j]} + p_{ba}^{[j]})\ln u_{ba}^{[j]}} - $ $\sum\nolimits_{(b,a) \in {\cal N}_j^{{u^ - }}} {(p_{ba}^{[j]}\delta _b^{[j]} + \pi _b^{[j]}p_{ba}^{[j]})\ln u_{ba}^{[j]}}>0$.
记$T_D^{[j]}({h_1},\bar h)$和${D^{[j]}}({h_1},\bar h)$分别为第$j$个子MJLS在区间$[{h_1},\bar h)$内的总驻留时间和总作用次数,则由式(26) 可得
\begin{align}&{\rm E}\left[{\ln V(\bar h)} \right]< \sum\limits_{j = 1}^M {{\beta ^{[j]}}{D^{[j]}}({h_1},\bar h)}+ \nonumber\\&\quad \sum\limits_{j = 1}^M {{\alpha ^{[j]}}T_D^{[j]}({h_1},\bar h)}+ {\rm E}\left[{\ln V({h_1})} \right] \end{align}
(27) 因此,由式(27) 依次类推可得
\begin{align}{\rm E}\left[{\ln V(k)} \right]&< \sum\limits_{j = 1}^M {{\beta ^{[j]}}{D^{[j]}}(0,k)} + \sum\limits_{j = 1}^M {{\alpha ^{[j]}}T_D^{[j]}(0,k)}+\nonumber\\&\quad {\rm E}\left[{\ln V(0) } \right]<\tilde \beta \sum\limits_{j = 1}^M {{D^{[j]}}(0,k)}+ \nonumber\\&\quad \tilde \alpha \sum\limits_{j = 1}^M {T_D^{[j]}(0,k)} +{\rm E}\left[{\ln V(0) } \right]=\nonumber\\&\quad \tilde \beta \theta (0,k) + \tilde \alpha k + {\rm E}\left[{\ln V(0) } \right]\end{align}
(28) 其中 $\tilde \alpha = {\max _{j \in {\cal M}}}\{ {\alpha^{[j]}}\}$ , $\tilde \beta = {\max _{j \in {\cal M}}}\{ {\beta^{[j]}}\}$ , $\sum\nolimits_{j = 1}^M {{D^{[j]}}(0,k)} = \theta(0,k)$ , $\sum\nolimits_{j = 1}^M {T_D^{[j]}(0,k)} = k$ , $\theta(0,k)$ 表示顶层切换 $\gamma (k)$ 在区间 $[0,k)$ 内的切换次数.
注意到 $0 \le \theta (0,k) \le \left\lceil {\frac{k}{{\tau + T}}}\right\rceil (T + 1) \le \left( {\frac{k}{{\tau + T}} + 1}\right)(T + 1) $ 和 $\tilde \beta > 0$ ,所以
\begin{align}&{\rm E}\left[{\ln V(k)} \right]<\tilde \beta \left({\frac{k}{{\tau+ T}} + 1} \right)(T + 1) + \tilde \alpha k +\notag\\&\quad {\rm E}\left[{\ln V(0) } \right]=k\left( {\frac{{\tilde \beta (T + 1) }}{{\tau + T}} + \tilde \alpha } \right) + \notag\\&\quad \tilde \beta (T + 1) + {\rm E}\left[{\ln V(0) }\right]\end{align}
(29) 又因为
\begin{align}&{\lambda _{\min }}(R_{{\sigma ^{\gamma (k)}}(k)}^{[\gamma(k)]}){\mathit{\boldsymbol{x}}}_k^{\rm T}{{\mathit{\boldsymbol{x}}}_k} \le {\mathit{\boldsymbol{x}}}_k^{\rm T}R_{{\sigma ^{\gamma (k)}}(t)}^{[\gamma (k)]}{{\mathit{\boldsymbol{x}}}_k} =V(k)\end{align}
(30) \begin{align}&\qquad \quad V(0) \le {\lambda _{\max }}(R_{{\sigma ^{\gamma(0) }}(0) }^{[\gamma (0)]}){\mathit{\boldsymbol{x}}}_0^{\rm T}{\mathit{\boldsymbol{x}}}_0^{}\end{align}
(31) 所以根据式(29) $\sim$ (31) ,得
\begin{align}&{\rm E}\left[{\ln \frac{{\left\| {{{\mathit{\boldsymbol{x}}}_k}} \right\|}}{{\left\| {{{\mathit{\boldsymbol{x}}}_0}} \right\|}}} \right] \le \frac{k}{2}\left( {\frac{{\tilde \beta (T + 1) }}{{\tau + T}} + \tilde \alpha } \right) + \frac{1}{2}\tilde \beta (T + 1) +\nonumber\\&\quad \frac{1}{2}\left( {{\rm E}[\ln {\lambda _{\max }}(R_{{\sigma^{\gamma (0) }}(0) }^{[\gamma (0)]})] - {\rm E}[\ln {\lambda _{\min}}(R_{{\sigma ^{\gamma (k)}}(k)}^{[\gamma (k)]})]} \right)\end{align}
(32) 又因为
\begin{align}\left\| {\Phi (k,0) } \right\|{\rm{ = }}\mathop {\max}\limits_{{\mathit{\boldsymbol{x}}}_0 \ne 0} \frac{{\left\| {\Phi (k,0) {{\mathit{\boldsymbol{x}}}_0}} \right\|}}{{\left\| {{{\mathit{\boldsymbol{x}}}_0}} \right\|}} = \mathop{\max }\limits_{{\mathit{\boldsymbol{x}}}_0 \ne 0} \frac{{\left\| {{{\mathit{\boldsymbol{x}}}_k}}\right\|}}{{\left\| {{{\mathit{\boldsymbol{x}}}_0}} \right\|}}\end{align}
(33) 则由式(32) $\sim$ (33) 和式(12) 可得
\begin{align}&{\rm E}\left[{\mathop {\lim }\limits_{k \to \infty } \sup\frac{1}{k}\ln \left\| {\Phi (k,0) } \right\|} \right]\!\!\le\!\! \frac{1}{2}\left( {\frac{{\tilde \beta (T + 1) }}{{\tau + T}} + \tilde \alpha } \right)\!\!+\nonumber\\&\qquad \mathop {\lim }\limits_{k \to \infty } \sup \frac{1}{{2k}}\left( {{\rm E}[\ln {\lambda _{\max }}(R_{{\sigma ^{\gamma (0) }}(0) }^{[\gamma (0)]})]} \right.-\nonumber\\&\qquad \left. { {\rm E}[\ln {\lambda _{\min }}(R_{{\sigma ^{\gamma (k)}}(k)}^{[\gamma (k)]})}]\right)=\nonumber\\& \qquad \frac{1}{2}\left( {\frac{{\tilde \beta (T + 1) }}{{\tau +T}} + \tilde \alpha } \right)< 0\end{align}
(34) 因此,根据引理1可知离散时间TSS (1) 是鲁棒EAS稳定的. \hfill $\square$
注 4. 在定理1中,如果 $T =0$ ~(即PDT切换中只存在 $\tau$ 部分),此时PDT切换将退化为DT切换.对应的条件(12) 将变为$\tau >-\tilde{\beta }/\tilde{\alpha }\text{ }$.
注 5. 在定理1中,由于需要设计参数 $\xi _{}^{[i]}$ , $s_r^{[i]}$ , $\lambda _r^{[i]}$ , $u_{qr}^{[i]}$ , $Q_r^{[i]}$ ,所以条件(8) $\sim$ (11) 是非凸的. 这些参数可以通过以下步骤得到:1) 求解不等式(8) $\sim$ (10) 得到最小的 $\lambda_r^{[i]}$ 和对应的 $\xi _{}^{[i]}$ , $s_r^{[i]}$ , $Q_r^{[i]}$ ;2) 将步骤1) 中得到的 $Q_r^{[i]}$ 和 $Q_q^{[i]}$ 代入不等式(11) 中,解得 $u_{qr}^{[i]}$ ; 3) 将得到的 $\lambda_r^{[i]}$ 和 $u_{qr}^{[i]}$ 代入到 ${\alpha ^{[j]}}$ 的表达式中,检查 ${\alpha ^{[j]}}$ 是否小于0. 如果 ${\alpha ^{[j]}} \ge 0$ ,增加 $\lambda _r^{[i]}$ 的值并重复以上步骤; 4) 根据上面得到的参数,并结合式(12) 得到使系统稳定的 $T$ 和 $\tau$ .
3. 仿真例子
考虑离散时间不确定TSS: ${{\mathit{\boldsymbol{x}}}_{k + 1}} = \bar A_{{\sigma^{\gamma (k)}}(k)}^{[\gamma (k)]}{{\mathit{\boldsymbol{x}}}_k}$ ,其中 $\gamma (k) =1,2$ , ${\sigma ^{\gamma (k)}}(k) = 1,2$ , $\bar A_i^{[j]} \in \{A_i^{[j]} + L_i^{[j]}\Delta _i^{[j]}N_i^{[j]}|\Delta _i^{[j]} \in{\bf R}{^{m_i^{[j]} \times p_i^{[j]}}},|| {\Delta _i^{[j]}} ||\le w_i^{[j]}\} $ . 各参数如下:
$\begin{align} & A_{1}^{[1]}=\left[ \begin{matrix} 0.8 & 0.1 \\ 0.5 & 0.3 \\ \end{matrix} \right],L_{1}^{[1]}=\left[ \begin{matrix} 1 & 2 \\ 1.2 & 1.5 \\ \end{matrix} \right] \\ & N_{1}^{[1]}=[1\quad 1]A_{2}^{[1]}=\left[ \begin{matrix} 0.2 & 0.5 \\ 0 & 0.3 \\ \end{matrix} \right], \\ & L_{2}^{[1]}=\left[ \begin{matrix} 1 & 1 \\ 1 & 1.5 \\ \end{matrix} \right]N_{2}^{[1]}=\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right] \\ & A_{1}^{[2]}=\left[ \begin{matrix} 0.2 & 0.5 \\ 0 & 0.1 \\ \end{matrix} \right], \\ & L_{1}^{[2]}=\left[ \begin{matrix} 1 & 2 \\ 1 & 1 \\ \end{matrix} \right] \\ & N_{1}^{[2]}=[1\quad 2] \\ & A_{2}^{[2]}=\left[ \begin{matrix} 0.5 & 0.3 \\ 0.4 & 0.2 \\ \end{matrix} \right], \\ & L_{2}^{[2]}=\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right] \\ & N_{2}^{[2]}=\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right] \\ \end{align}$
扰动半径为 $w_1^{[1]} = 0.2$ , $w_2^{[1]} = 0.25$ , $w_1^{[2]} =0.35$ , $w_1^{[2]} = 0.3$ . 不确定矩阵如下:
$\begin{align} & \Delta _{1}^{[1]}=\left[ \begin{matrix} 0.2\sin (0.4k) \\ 0.2\cos (0.4k) \\ \end{matrix} \right] \\ & \Delta _{2}^{[1]}=\left[ \begin{matrix} 0.25\cos (0.1k) & 0 \\ 0 & 0.25\sin (0.5k) \\ \end{matrix} \right] \\ & \Delta _{1}^{[2]}=\left[ \begin{matrix} 0.35\sin (0.5k) \\ 0.35\cos (0.5k) \\ \end{matrix} \right] \\ & \Delta _{2}^{[2]}=\left[ \begin{matrix} 0.3\cos (0.05k) & 0 \\ 0 & 0.3\sin (0.05k) \\ \end{matrix} \right] \\ \end{align}$
Markov链 $\{ {\sigma ^1}(k)\} $ 和 $\{ {\sigma ^2}(k)\}$ 的一步转移概率矩阵分别为
${P^{[1]}} = \left[{\begin{array}{*{20}{c}}{0.2}&{0.8}\\{0.6}&{0.4}\end{array}} \right], {P^{[2]}} = \left[{\begin{array}{*{20}{c}}{0.5}&{0.5}\\{0.7}&{0.3}\end{array}} \right]$
对应的平稳分布分别是π[1] = [3/7 4/7], π[2] = [7/12 5/12].
应用Matlab LMI工具箱求解式(8) $\sim$ (11) ,可得
$\begin{align} & Q_{1}^{[1]}=\left[ \begin{matrix} 0.4001 & -0.2032 \\ -0.2032 & 0.8502 \\ \end{matrix} \right] \\ & Q_{2}^{[1]}=\left[ \begin{matrix} 0.5340 & -0.2806 \\ -0.2806 & 0.8005 \\ \end{matrix} \right] \\ & Q_{1}^{[2]}=\left[ \begin{matrix} 0.1076 & -0.0643 \\ -0.0643 & 1.2035 \\ \end{matrix} \right] \\ & Q_{2}^{[2]}=\left[ \begin{matrix} 0.7198 & -0.1770 \\ -0.1770 & 1.0850 \\ \end{matrix} \right] \\ \end{align}$
$\xi _{}^{[1]} = 1.8$ , $\xi _{}^{[2]} = 1.5$ , $s_1^{[1]} = - 2$ , $s_2^{[1]} = 2$ , $s_1^{[2]} = - 2$ , $s_2^{[2]} = - 2$ , $\lambda_1^{[1]} = 0.1$ , $\lambda _2^{[1]} = 1.5$ , $\lambda _1^{[2]} =0.2$ , $\lambda _2^{[2]} = 1$ , $u_{12}^{[1]} = 0.1$ , $u_{21}^{[1]}= 0.1$ , $u_{12}^{[2]} = 0.3$ , $u_{21}^{[2]} = 0.1$ .
由附录A可得 $\delta _1^{[1]} = \delta _2^{[1]} = 0.7143$ , $\delta_1^{[2]} = \delta _2^{[2]} = 0.8333$ .
则 ${\alpha ^{[1]}} = - 2.334$ , $ {\beta ^{[1]}} = 2.535$ , ${\alpha ^{[2]}} = - 1.9616$ , ${\beta ^{[2]}} = 4.614$ , $\tilde\alpha = - 1.9616$ , $\tilde \beta = 4.614$ .
由条件(12) 可得,当 $T$ 和 $\tau $ 满足 $T < 0.74\tau -1.74$ 时,不确定TSS是鲁棒EAS稳定的. 不妨选取 $T = 13$ , $\tau = 20$ ,并选择如下一个满足PDT约束的周期切换信号 $\gamma (k)$ :
$\gamma (k) = \left\{ {\begin{array}{*{20}{lllllllllllllll}}{1,\quad k \in [mK,mK + 22]} \\{2,\quad k \in [mK + 23,mK + 26]}\\{1,\quad k \in [mK + 27,mK + 30]}\\{2,\quad k \in [mK + 31,mK + 34]}\end{array}} \right. $
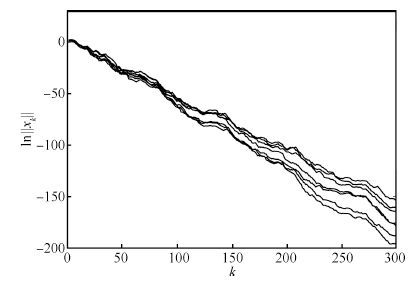
其中 $m = 0,1,2,\cdots $ ,周期 $K = 35$ . 图 5为顶层切换 $\gamma(k)$ 的切换序列,图 6 给出了由 ${{\mathit{\boldsymbol{x}}}_0} = {[3\quad -1]^{\rm T}}$ 开始的 $\ln \left\| {{{\mathit{\boldsymbol{x}}}_k}} \right\|$ 的7次样本实现,显然TSS是鲁棒EAS稳定的.
4. 结论
本文提出了一类新型的切换系统---两层切换系统(Two-level switched systems,TSSs). 该系统顶层切换是确定性的,底层切换服从多个Markov链. TSS可以用于一类具有分层结构复杂系统的建模与控制设计.针对顶层切换满足PDT约束,且系统存在参数不确定性的TSS,研究了其鲁棒EAS稳定性问题. 但在TSS中,由于顶层切换所对应的底层切换分别是由不同的Markov链控制,底层Markov链将无法达到稳定状态,Markov链的遍历性不再适用.本文基于Markov链的暂态特性给出了TSS鲁棒EAS稳定性的充分条件.最后用一个数值仿真例子验证了文中方法的有效性.
附录A
证明 . 由于
\begin{align}&\left( {\sum\limits_{j = 1}^k {{P^j}} } \right)\left( {P - I}\right) = \left( {P + {P^2} + \cdots + {P^k}} \right)\times\nonumber\\&\qquad \left( {P - I} \right)= {P^{k + 1}} - P \end{align}
(A1) 而另一方面
\begin{align}& \left( {\sum\limits_{j = 1}^k {{P^j}} } \right)\left( {P - I} \right)= \nonumber\\&~~~ \left( {\sum\limits_{j = 1}^k {{P^j}} } \right)\left( {P - I - {{1}_{N \times N}} + {{1}_{N \times N}}} \right)= \nonumber\\&~~~ \left( {\sum\limits_{j = 1}^k {{P^j}} } \right)\left( {P - I- {{1}_{N \times N}}} \right) \!\!+\!\!\left( {\sum\limits_{j = 1}^k {{P^j}} } \right){{1}_{N \times N}}\!=\nonumber\\&~~~ \left( {\sum\limits_{j = 1}^k {{P^j}} } \right)\left( {P - I- {{1}_{N \times N}}} \right) + k{{1}_{N \times N}}\end{align}
(A2) 所以
\begin{align}&{P^{k + 1}} - P =\nonumber\\&\quad \left( {\sum\limits_{j = 1}^k {{P^j}} } \right)\left( {P -I - {{1}_{N \times N}}} \right) + k{{1}_{N \times N}}\end{align}
(A3) 即
\begin{align}&P - {P^{k + 1}} + k{{1}_{N \times N}}=\nonumber\\&\quad \left( {\sum\limits_{j = 1}^k {{P^j}} } \right)\left( {I -P + {{1}_{N \times N}}} \right)\end{align}
(A4) 由文献[18]中命题2.14.1,矩阵 $P - I + {{1}_{N \times N}}$ 可逆且满足 $ {\pi} = {{1}_{1 \times N}}{(I - P + {{1}_{N\times N}})^{ - 1}}$ ,所以由式(A4) ,
\begin{align*}&\sum\limits_{j = 1}^k {{P^j}} = \left( {P - {P^{k + 1}}} \right){\left( {I - P + {{1}_{N \times N}}} \right)^{ - 1}} +\nonumber\\&\quad k{{1}_{N \times N}}{\left( {I - P + {{1}_{N \times N}}} \right)^{ - 1}}=\nonumber\\&\quad \left( {P - {P^{k + 1}}} \right){\left( {I - P + {{1}_{N\times N}}} \right)^{ - 1}}+\nonumber\\&\quad k{{1}_{N \times 1}}{{1}_{1 \times N}}{\left( {I - P + {{1}_{N \times N}}} \right)^{ - 1}}=\nonumber\\&\quad \left( {P - {P^{k + 1}}} \right){\left( {I - P + {{1}_{N\times N}}} \right)^{ - 1}} + k{{1}_{N \times 1}}{\pi} \end{align*}
(A5) 注意到 ${\pi} = {\pi} P$ ,则由式(A5) 可得
\begin{align}&( {f} - {\pi}){\left[{\sum\limits_{j = 1}^k {{P^j}} }\right]_i}= ( {f} - {\pi} )\times\notag\\&\quad {\left[{(P - {P^{k + 1}}){{(I - P + {{1}_{N \times N}})}^{ - 1}} + k{{1}_{N \times 1}}{\pi} } \right]_i}=\notag\\&\quad ( {f} - {\pi} ){\left[{(P - {P^{k + 1}}){{(I - P + {{1}_{N \times N}})}^{ - 1}}} \right]_i}+\nonumber\\&\quad k{\pi_i}( {f} - {\pi} ){{1}_{N \times 1}}=\nonumber\\&\quad {f}{\left[{(P - {P^{k + 1}}){{(I - P + {{1}_{N \times N}})}^{ - 1}}} \right]_i}\end{align}
(A6) 下面计算在任意 ${f}$ 和 $k$ 的情况下, ${f_i}{p_{ij}}$ 和 $( {f} - {\pi})\times$ ${\left[{\sum\nolimits_{j = 1}^k {{P^j}} }\right]_i}$ 的取值范围:
1) 对于任意 ${f}$ ,显然
\begin{align}0 \le {f_i}{p_{ij}} \le {p_{ij}}\end{align}
(A7) 2) 记 $[{c_1}~~~{c_2} \cdots {c_N}]: = {f}(P - {P^{k +1}})$ 和 $[{b_{1i}}~~~{b_{2i}} \cdots $ ${b_{Ni}}]: = {[{(I - P +{{1}_{N \times N}})^{ - 1}}]_i}$ . 显然,当 $P$ 给定时 ${b_{ji}}$ 是常数,且对于任意的 ${f}$ 和 $k$ , $\sum\nolimits_{i = 1}^N {{c_i}} = 0,$ $ - 1 \le {c_i} \le 1$ .所以
\begin{align}( {f} - {\pi} ){\left[{\sum\limits_{j = 1}^k {{P^j}} } \right]_i}= \sum\limits_{j = 1}^N {{c_j}{b_{ji}}} \end{align}
(A8) 因此,对于任意的初始概率 ${f}$ 和时间 $k$ , $( {f} - {\pi} )$ ${\times\left[{\sum\nolimits_{j = 1}^k {{P^j}} }\right]_i}$ 的最大、最小值可由下面的线性规划问题得到:
$\mathop {\max }\limits_{{c_1},\cdots ,{c_N}} \sum\limits_{i = 1}^N {{c_i} {b_{ij}} }( {\rm or} \mathop {\min }\limits_{{c_1},\cdots ,{c_N}}\sum\limits_{i = 1}^N {{c_i} {b_{ij}}} )$$\begin{array}{l}{\rm s.{\rm{ }}t.} \sum\limits_{i = 1}^N {{c_i}} = 0\\ - 1 \le {c_i} \le 1, i = 1,2,\cdots ,N\end{array}$
记 ${\delta _i}:= \!\mathop {\max }\limits_{{c_1},\cdots ,{c_N}} \sum\nolimits_{j = 1}^N {{c_j}{b_{ji}}} $ ,显然 $\mathop {\min}\limits_{{c_1},\cdots ,{c_N}} \sum\nolimits_{j = 1}^N{{c_j}{b_{ji}}}= -{\delta _i}$ . 则由 ${\delta _i}$ ,式(A6) $\sim$ (A8) 和引理2可得式(6) 和式(7) . $\square$
-
[1] Briat C, Seuret A. Affine characterizations of minimal and mode-dependent dwell-time for uncertain switched linear systems. IEEE Transactions on Automatic Control, 2013, 58(5):1304-1310 doi: 10.1109/TAC.2012.2220031 [2] Zhao X D, Zhang L X, Shi P, Liu M. Stability and stabilization of switched linear systems with mode-dependent average dwell time. IEEE Transactions on Automatic Control, 2012, 57(2):1809-1815 http://ieeexplore.ieee.org/document/6097035/ [3] Hespanha J P. Uniform stability of switched linear systems:extensions of LaSalle's invariance principle. IEEE Transactions on Automatic Control, 2004, 49(4):470-482 doi: 10.1109/TAC.2004.825641 [4] Zhang L X, Zhuang S L, Shi P. Non-weighted quasi-time-dependent H∞ filtering for switched linear systems with persistent dwell-time. Automatica, 2015, 54:201-209 doi: 10.1016/j.automatica.2015.02.010 [5] Zhu J, Wang L P, Spiryagin M. Control and decision strategy for a class of Markovian jump systems in failure prone manufacturing process. IET Control Theory & Applications, 2012, 6(12):1803-1811 [6] Mao Z, Jiang B, Shi P. H∞ fault detection filter design for networked control systems modelled by discrete Markovian jump systems. IET Control Theory & Applications, 2007, 1(5):1336-1343 http://ieeexplore.ieee.org/document/4293139/keywords [7] 马卫国, 邵诚. 网络控制系统随机稳定性研究. 自动化学报, 2007, 33(8):878-882 http://www.aas.net.cn/CN/abstract/abstract17261.shtmlMa Wei-Guo, Shao Cheng. Stochastic stability for networked control systems. Acta Automatica Sinica, 2007, 33(8):878-882 http://www.aas.net.cn/CN/abstract/abstract17261.shtml [8] Xiao N, Xie L H, Fu M Y. Stabilization of Markov jump linear systems using quantized state feedback. Automatica 2010, 46(10):1696-1702 doi: 10.1016/j.automatica.2010.06.018 [9] Bolzern P, Colaneri P, De Nicolao G. Stochastic stability of positive Markov jump linear systems. Automatica 2014, 50(4):1181-1187 doi: 10.1016/j.automatica.2014.02.016 [10] Fang Y G, Loparo K A. Stabilization of continuous-time jump linear systems. IEEE Transactions on Automatic Control, 2002, 47(10):1590-1603 doi: 10.1109/TAC.2002.803528 [11] Song Y, Dong H, Yang T C, Fei M R. Almost sure stability of discrete-time Markov jump linear systems. IET Control Theory & Applications, 2014, 8(11):901-906 [12] Xiong J L, Lam J, Shu Z, Mao X R. Stability analysis of continuous-time switched systems with a random switching signal. IEEE Transactions on Automatic Control, 2014, 59(1):180-186 doi: 10.1109/TAC.2013.2266751 [13] Bolzern P, Colaneri P, De Nicolao G. Almost sure stability of Markov jump linear systems with deterministic switching. IEEE Transactions on Automatic Control, 2013, 58(1):209-214 doi: 10.1109/TAC.2012.2203049 [14] Bolzern P, Colaneri P, De Nicolao G. Markov jump linear systems with switching transition rates:mean square stability with dwell-time. Automatica, 2010, 46(6):1081-1088 doi: 10.1016/j.automatica.2010.03.007 [15] 盖彦荣, 陈阳舟, 张亚霄. 切换信息拓扑和时变时滞下离散时间线性多智能体系统一致性的平均驻留时间条件. 自动化学报, 2014, 40(11):2609-2617 doi: 10.1016/S1874-1029(14)60407-9Ge Yan-Rong, Chen Yang-Zhou, Zhang Ya-Xiao. Average dwell-time conditions for consensus of discrete-time linear multi-agent systems with switching topologies and time-varying delays. Acta Automatica Sinica, 2014, 40(11):2609-2617 doi: 10.1016/S1874-1029(14)60407-9 [16] Tanelli M, Picasso B, Bolzern P, Colaneri P. Almost sure stabilization of uncertain continuous-time Markov jump linear systems. IEEE Transactions on Automatic Control, 2010, 55(1):195-201 doi: 10.1109/TAC.2009.2033844 [17] Bolzern P, Colaneri P, De Nicolao G. On almost sure stability of continuous-time Markov jump linear systems. Automatica, 2006, 42(6):983-988 doi: 10.1016/j.automatica.2006.02.007 [18] Resnick S I. Adventures in Stochastic Processes. Basel, Switzerland:Birkhäuser Verlag, 1992. 期刊类型引用(4)
1. 席敏,龙飞. 离散双切换线性正系统的L1增益性能分析. 自动化仪表. 2022(02): 23-29 .  百度学术
百度学术2. 冉晓宇,龙飞. 连续双切换线性正系统状态反馈控制. 智能计算机与应用. 2022(07): 118-122 .  百度学术
百度学术3. 丁文淞,龙飞,穆倩倩. 一类具有不确定性双切换系统的鲁棒镇定. 广西大学学报(自然科学版). 2021(05): 1349-1359 .  百度学术
百度学术4. 赵娜,熊建栋,伍俊. 一类切换线性系统的慢切换镇定设计. 数学的实践与认识. 2019(24): 195-201 .  百度学术
百度学术其他类型引用(16)
-






 下载:
下载:


 下载:
下载:
