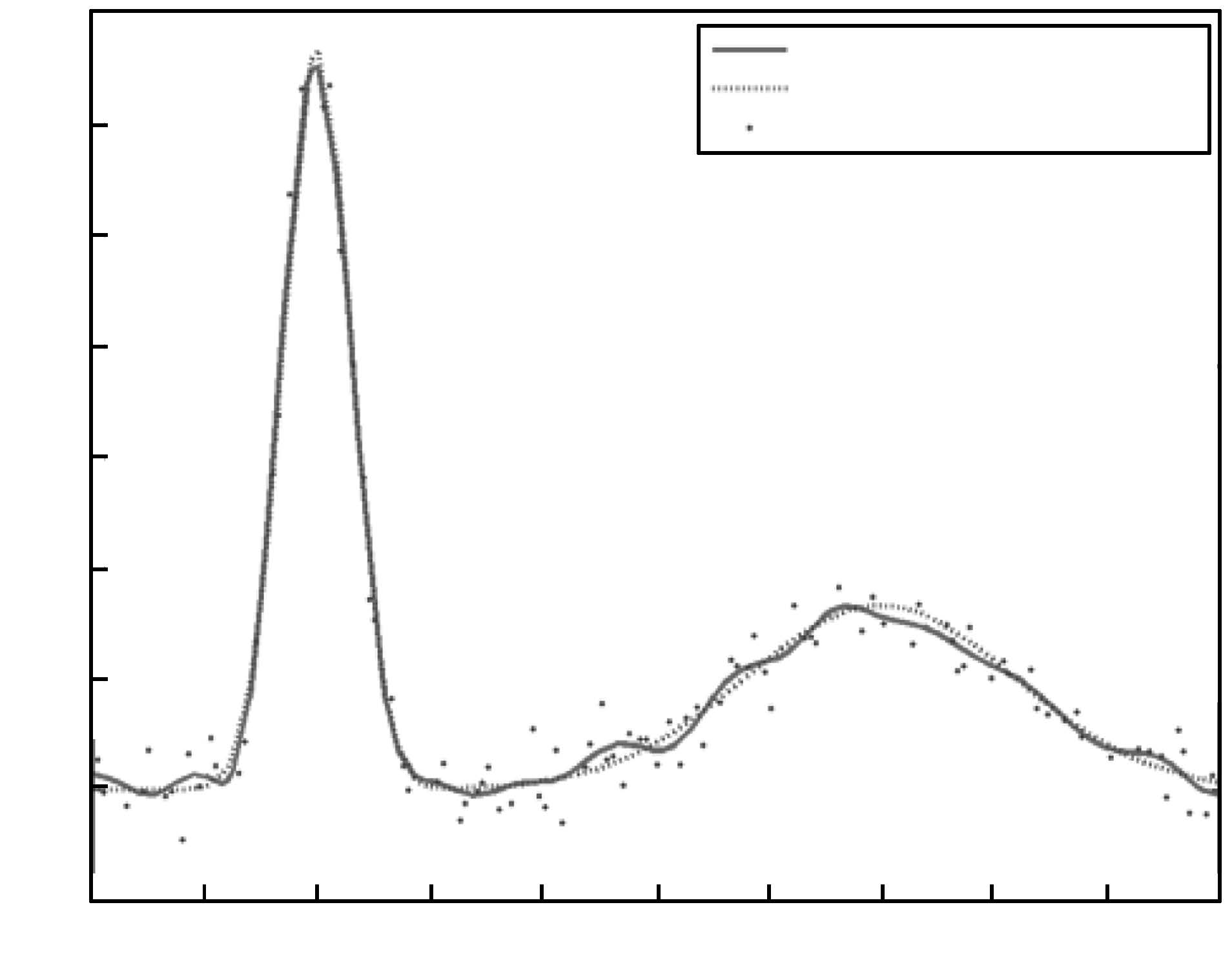
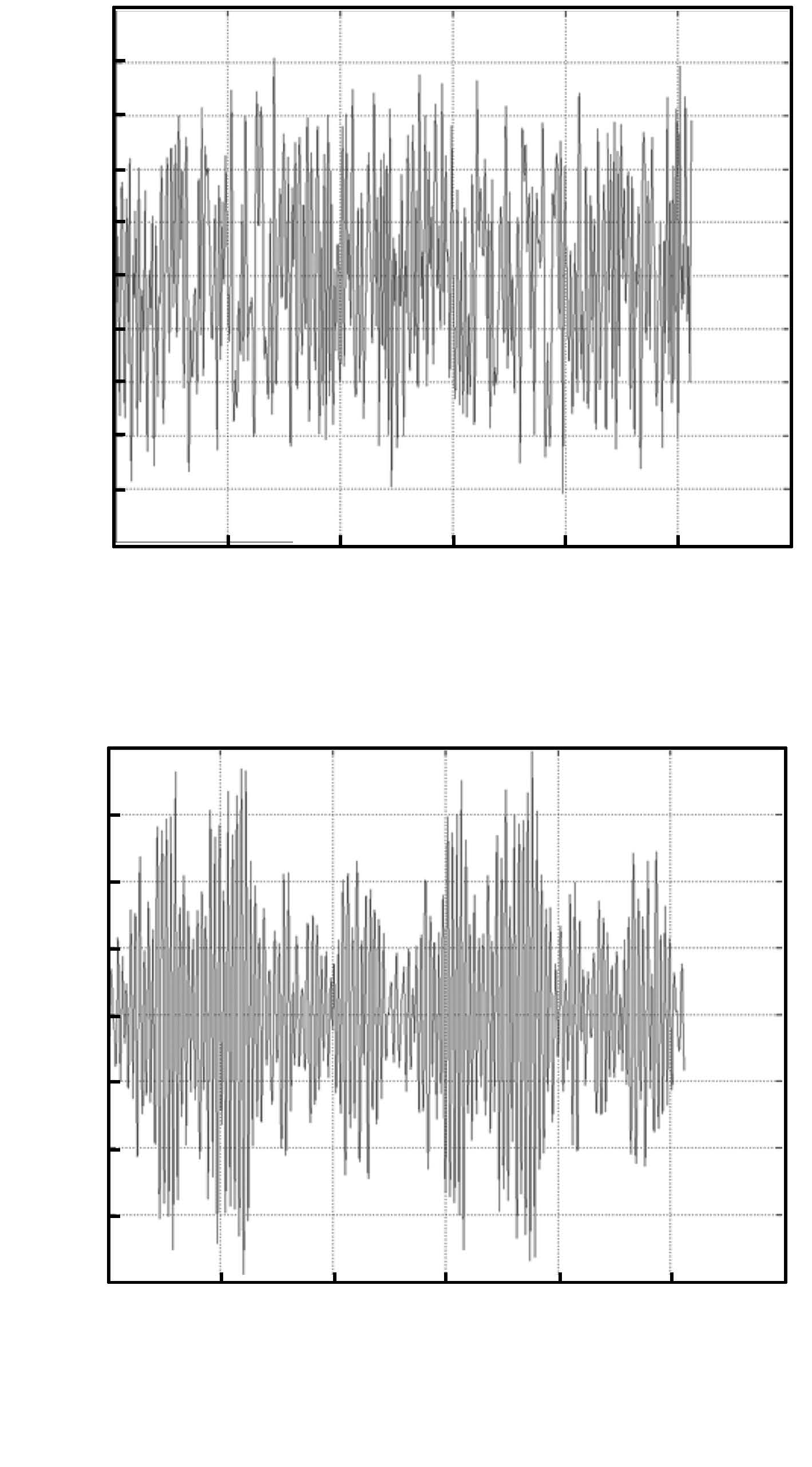
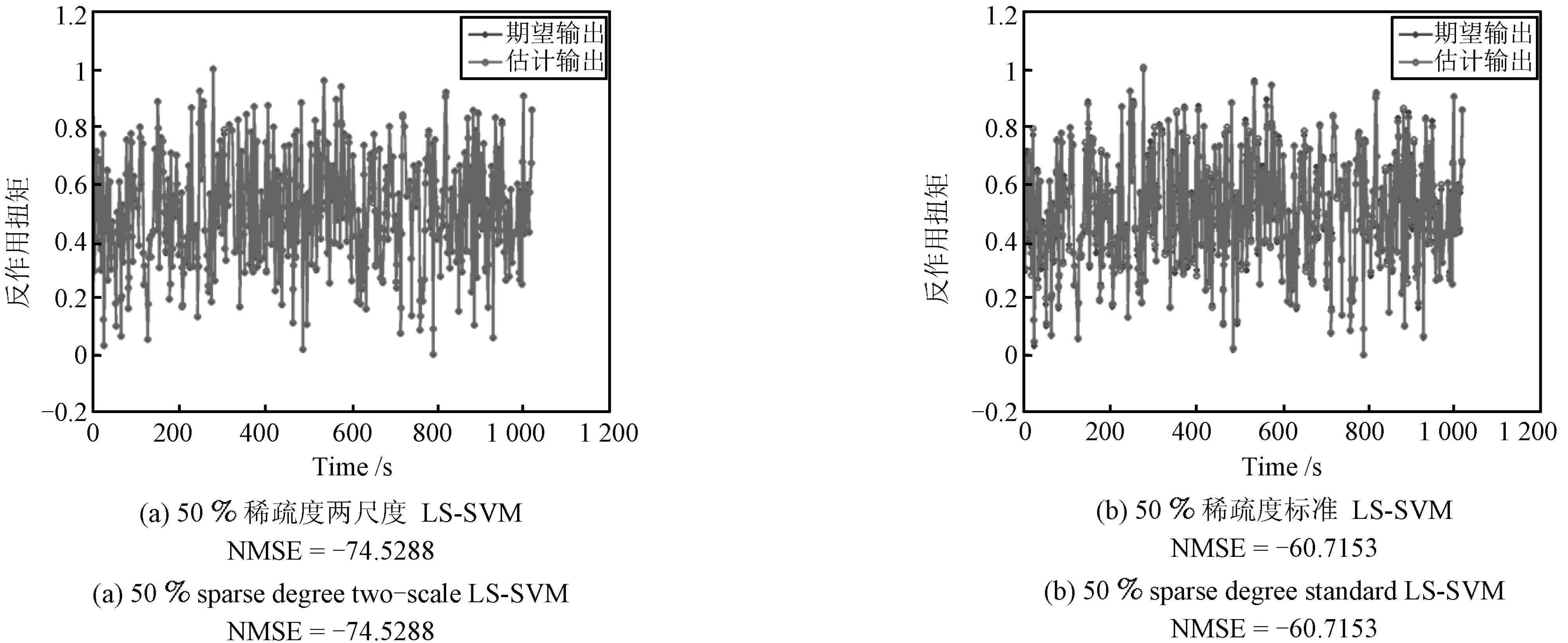
-
摘要: 提出一种基于压缩感知(Compressive sensing, CS)和多分辨分析(Multi-resolution analysis, MRA)的多尺度最小二乘支持向量机(Least squares support vector machine, LS-SVM). 首先将多尺度小波函数作为支持向量核, 推导出多尺度最小二乘支持向量机模型, 然后基于压缩感知理论, 利用最小二乘匹配追踪(Least squares orthogonal matching pursuit, LS-OMP)算法对多尺度最小二乘支持向量机的支持向量进行稀疏化, 最后用稀疏的支持向量实现函数回归. 实验结果表明, 本文方法利用不同尺度小波核逼近信号的不同细节, 而且以比较少的支持向量能达到很好的泛化性能, 大大降低了运算成本, 相比普通最小二乘支持向量机, 具有更优越的表现力.Abstract: A multi-scale least squares support vector machine (LS-SVM) based on compressive sensing (CS) and multi-resolution analysis (MRA) is proposed. First, a multi-scale LS-SVM model is conducted, in which a support vector kernel with the multi-resolution wavelet function is employed; then inspired by CS theory, sparse support vectors of multi-scale LS-SVM are constructed via least squares orthogonal matching pursuit (LS-OMP); finally, sparse support vectors are applied to function approximation. Simulation experiments demonstrate that the proposed method can estimate diverse details of signal by means of wavelet kernel with different scales. What is more, it can achieve good generalization performance with fewer support vectors, reducing the operation cost greatly, performing more superiorly compared to ordinary LS-SVM.
-
压缩感知(Compressive sensing, CS)理论作为一种新的信息获取手段, 可基于信号结构的稀疏特性, 在远低于奈奎斯特采样率的条件下, 通过少数量测值实现对信号的精确重建 [1-2]. 由于能够有效缓解数据传输、 存储和处理等方面的压力, 相关的研究成果已涉及到图像 [3]、通信 [4]和雷达 [5] 等众多领域 [6]. 稀疏重建算法作为CS 的核心内容之一, 在一定程度上决定着能否将CS 推向实用化 [7]. 传统的重建算法及相关研究大多是针对一维实信号 [8]. 然而在实际应用场景中, 如阵列信号处理 [9]、SAR [10-11]、ISAR (Inverse synthetic aperture radar) [12] 和磁共振成像 [13] 等, 待处理的往往是多维复数信号. 目前对多维信号的处理主要有以下三种思路: 1)将多维信号列向量化为一维; 然后, 利用一维重建算法进行处理, 但是这种处理会使得感知矩阵规模急剧变大, 显著增加计算复杂度. 2)基于Kronecker 积CS的思想 [14], 其主要通过构建可分离感知算子降低算法的复杂度, 实际上, 利用小规模量测矩阵的Kronecker 积对向量化的多维信号采样与利用小规模量测矩阵进行逐一采样是等价的. 3)利用信号的联合结构特性进行多维处理. 如文献[15] 基于信号的块稀疏特征, 将二维信号分为更小的块, 然后利用块对角量测矩阵代替原始密集的量测矩阵进行采样, 有效地降低了存储空间和计算复杂度. 文献[16]基于二维信号的联合稀疏特征, 利用同一个感知矩阵进行重建. 但是当二维信号的稀疏结构具有任意性时, 文献[15-16]所提算法的性能将变差. 针对这一问题, 文献[17]提出利用并行CS方案进行并行感知, 并放松了对应的RIP (Restricted isometry property)条件. 但文献[17]依然是对二维信号每列逐一重建, 计算复杂度仍然较高, 且该方法是在实数情况下讨论的, 若在复信号情况下利用该方法, 则需利用文献[10] 的实数化方法, 存储空间和计算复杂度会进一步增加.
而目前对复数信号重建主要有两种思路: 1)将复信号的实部和虚部排列为实数化的信号后进行重建的思路 [10], 该方法会增加信号以及感知矩阵的规模, 造成存储空间和计算量增加. 2)文献[8]采取迭代交替估计幅度和相位的思路进行复信号重建, 但这种方法相当于两次优化过程, 增加了计算复杂度.
为有效实现对二维复稀疏信号的快速重建, 本文在线性Bregman 迭代(Linearized Bregman iteration, LBI) 的基础上, 提出一种快速并行重建复稀疏信号的并行线性Bregman迭代(Parallel fast linearized Bregman iteration, PFLBI)算法. 首先, 构建了二维复稀疏信号的结构模型, 详细分析了其信号结构特征; 其次, 从理论上推导了对二维复稀疏信号并行重建的并行Bregman迭代格式; 然后, 采用估计迭代步长的方法加快收敛过程以提高运算速度; 最后, 对PFLBI算法的收敛性, 抗噪性和计算复杂度进行分析, 仿真结果验证了理论分析的正确性. 将PFLBI 算法应用于ISAR 成像中, 仿真和实测数据成像结果都验证了算法的良好性能.
1. 二维复稀疏信号模型
对于一个二维复稀疏信号, 可以用矩阵形式来表示, 假设二维复稀疏信号 $X\in {{C}^{N\times D}}$只有 K 个非零元素, 此时称 X 是 K 稀疏的, X 的稀疏程度可以用稀疏度向量 ${ K}=[K_1, K_2, \cdots, K_d, \cdots, K_D]$ 来表示, 其中 Kd 表示 X 的第 d 列的稀疏度, 显然有 $K=\|{ K}\|_1$. 图 1给出了二维复稀疏信号的示意图. 图 1 (a)给出了信号的幅度和位置, 为更清晰地描述信号结构, 图 1 (b)给出了信号的位置关系图, 其中黑点表示该点为非零元素, 白点表示该点为零元素. 可以看出, 当二维复稀疏信号具有任意稀疏结构时, 其每一列的稀疏度和非零元素的位置都是任意的. 而二维复稀疏信号的重建可表示为如下的数学问题:
$Y=\Theta X$
(1) 其中, $ Y=[{ y}_1, {{ y}_{2}}, \cdots , {{ y}_{D}}] $为二维的量测值矩阵, $X=\left[{{ x}_{1}}, {{ x}_{2}}, \cdots , {{ x}_{D}} \right]$ 为待重建的二维稀疏矩阵, 此时可以利用并行CS方案进行求解 [17], 事实上, 式(1)可等效为 D 个一维复稀疏信号重建, 即
${{ y}_d}=\Theta {{ x}_{d}} , \qquad d=1, \cdots , D$
(2) 其中, ${ y}_d\in C^{M}$为第 d 列量测向量, D 为二维复稀疏信号的总列数, ${{ x}_{d}}\in {C^{N}}$ 为待重建的第 d 列一维复稀疏向量.
利用X的稀疏特性约束, 求解式(1)的稀疏解问题可以描述为如下优化问题 [18]:
$\underset{X\in {C^{N\times D}}}{\mathop{\min }} {{\left\| X \right\|}_{0, q}} {\rm s. t.} Y=\Theta X$
(3) 其中, ${{\left\| X \right\|}_{0, q}}=\left| {\rm supp}\left( X \right) \right|$, ${\rm supp}\left( X \right)$ 为 X 的支撑集, 即非零元素的个数. 文献[17]证明了利用并行CS方案时, 若感知矩阵 $\Theta$ 满足RIP条件, 则二维复稀疏信号 X 能够从量测值 Y 中精确重建出来. 由于式(3)是NP难的问题, 在感知矩阵 $\Theta$ 满足RIP条件下, 可将式(3)转化为以下凸优化问题 [18]:
$\underset{X\in {C^{N\times D}}}{\mathop{\min }} {{\left\| X \right\|}_{1}} {\rm s. t.} Y=\Theta X$
(4) 其中, 矩阵的1-范数定义为 ${{\left\| X \right\|}_{1}}=\sum\nolimits_{i=1}^{N}{\sum\nolimits_{j=1}^{N}{\left| {{X}_{i, j}} \right|}}$.
考虑到实际中存在噪声, 为从含有噪声的量测值 Y 中恢复稀疏信号 X, 放松式(4)的约束项, 利用正则化参数 $\mu$ 控制稀疏度和误差, 转化为如下正则化形式 [19]:
$\hat{X}={\rm arg}\underset{X\in {C^{N\times D}}}{\mathop{\rm min}} \mu {{\left\| X \right\|}_{1}}\text{+}\frac{1}{2}\left\| \Theta X-Y \right\|_{\rm F}^{2} $
(5) 其中, ${{\left\| \cdot \right\|}_{\rm F}}$ 表示矩阵的Frobenius范数, 简称 $\rm F$ 范数, 定义如下 [20]:
${{\left\| A \right\|}_{\text{F}}}={{\left( \sum\limits_{i, j=1}^{N}{{{\left| {{a}_{ij}} \right|}^{2}}} \right)}^{\frac{1}{2}}}=\text{tr}\left( {{A}^{\text{H}}}A \right)$
(6) 其中, $\text{tr}\left( \cdot \right)$为矩阵的迹, 即对角线元素之和.
2. PFLBI 算法
为高效准确地求解式(5), 本文提出PFLBI算法, 该算法主要包括两个方面: 1)构建PFLBI算法基本迭代格式, 即将LBI拓展到二维复稀疏信号模型中, 实现对二维复稀疏信号的并行重建; 2)快速实现, 即通过迭代步长的估计提高收敛速度, 有效避免处理时造成的冗余计算, 提高运算速度. 下面进行具体介绍和分析.
2.1 PFLBI 算法基本迭代格式
PFLBI算法基本迭代格式的构建主要包括两部分: 1)利用Bregman距离得到求解式(5)的Bregman迭代; 2)将求解式(5)的Bregman迭代线性化, 得到复矩阵形式的LBI. 首先给出求解式(5)的PFLBI算法基本迭代格式, 然后再对其证明.
采用LBI求解式(5)的最终迭代结果可表示为
${{V}^{k+1}}={{V}^{k}}+{{\Theta }^{\text{H}}}(Y-\Theta \text{ }{{X}^{k}})\ {{X}^{k+1}}\text{ = }\delta \text{sof}{{\text{t}}_{\mu }}({{V}^{k+1}})$
(7) 其中, ${{X}^{k+1}} $为迭代输出, ${{V}^{k+1}} $为中间变量, ${{X}^{0}}={{V}^{0}}=0$, $k=0$, $\text{\rm soft}\left( \cdot \right)$ 为复矩阵条件的软阈值算子, 定义如下:
$\eqalign{ &{\rm{sof}}{{\rm{t}}_\mu }({\rm{V}}){\rm{ = }}{{\max \left\{ {\left| {{{\rm{V}}_{{\rm{ij}}}}} \right|{\rm{0}}\mu , {\rm{0}}} \right\}} \over {\max \left\{ {\left| {{{\rm{V}}_{{\rm{ij}}}}} \right|{\rm{0}}\mu , {\rm{0}}} \right\}{\rm{ + }}\mu }} \cr &{{\rm{V}}_{{\rm{ij}}}}{\rm{ = }}\left\{ \matrix{ {{{V_{ij}}} \over {\left| {{V_{ij}}} \right|}}\left( {\left| {{V_{ij}}} \right| - \mu } \right), \left| {{V_{ij}}} \right| > \mu \hfill \cr 0, \left| {{V_{ij}}} \right| \le \mu \hfill \cr} \right. \cr} $
(8) 其中, ${{V}_{ij}}$为复数矩阵V中第i行第j列的元素, $\left| {{V}_{ij}} \right|$表示${{V}_{ij}}$的模. 在对上式进行证明之前, 首先给出两个定义: 1)不可微凸函数 $J\left( X \right) $在点 $X $处的次微分定义为 [21]
$\partial J\left( X \right):=\{P|J\left( V \right)\ge J\left( X \right)+\left\langle P, V-X \right\rangle , \forall V\in S\}$
(9) 其中, $S $为 $J\left( X \right) $的可行域, $\left\langle \cdot , \cdot \right\rangle $为内积, 矩阵 $P\in \partial J\left( X \right) $ 称为 $J\left( X \right) $在点 $X $处的次梯度.
2)凸函数 $J\left( X \right) $ 上的点 X 和 V 的Bregman距离定义为 [22]
$D_{J}^{P}\left( X, V \right)=J\left( X \right)-J\left( V \right)-\left\langle P, X-V \right\rangle $
(10) 其中, 向量 $P\in \partial J\left( V \right) $为凸函数 $J\left( X \right) $ 在点 $V $的次微分中的一个次梯度.
用 $J\left( X \right) $的Bregman距离代替 $J\left( X \right) $, 可得到式(5)对应的Bregman迭代形式:
${{X}^{k+1}}=\text{arg}\underset{X\in {{C}^{N\times D}}}{\mathop{\text{min}}}\, D_{J}^{{{p}^{k}}}\left( X, {{X}^{k}} \right)+\frac{1}{2}\text{tr}{{\left( \Theta X-Y \right)}^{\text{H}}}\left( \Theta X-Y \right)$
(11) %11 现对矩阵形式的Bregman迭代正则化方法线性化, 将 $\frac{1}{2}\left\| \Theta X-Y \right\|_{\rm F}^{2} $在 ${{X}^{k}} $处进行一阶泰勒级数展开, 忽略常数项, 则式(11)变为
$\begin{align} &{{X}^{k+1}}=\text{arg}\underset{X\in {{C}^{N\times D}}}{\mathop{\text{min}}}\, D_{J}^{{{P}^{k}}}\left( X, {{X}^{k}} \right)+ \\ &\left\langle X, {{\Theta }^{\text{H}}}\left( \Theta {{X}^{k}}-y \right) \right\rangle +\frac{1}{2}\text{tr}{{\left( \Theta X-Y \right)}^{\text{H}}}\left( \Theta X-Y \right) \\ \end{align}$
(12) 令
$\begin{align} &F\left( X \right)=D_{J}^{{{P}^{k}}}\left( X, {{X}^{k}} \right)+\left\langle X, {{\Theta }^{\text{H}}}\left( \Theta {{X}^{k}}-y \right) \right\rangle \\ &+\frac{1}{2}\text{tr}\left( {{\left( X-{{X}^{k}} \right)}^{\text{H}}}\left( X-{{X}^{k}} \right) \right) \\ \end{align}$
(13) 根据平稳点的次微分条件, 有 $0\in \partial F\left( X \right) $, 则
$0\in \partial F\left( X \right)=\partial J\left( X \right)-{{P}^{k}}+\frac{1}{\delta }\left( X-\left( {{X}^{k}}-\delta {{\Theta }^{\text{H}}}\left( \Theta {{X}^{k}}-Y \right) \right) \right)$
(14) 在 $X={{X}^{k+1}} $处有 ${{P}^{k+1}}\in \partial J\left( {{X}^{k+1}} \right) $, 所以有:
${{P}^{k+1}}={{P}^{k}}-\frac{1}{\delta }\left( {{X}^{k+1}}-{{X}^{k}} \right)-{{\Theta }^{\text{H}}}\left( \Theta {{X}^{k}}-Y \right)$
(15) 利用递推公式可将式(15)写为
$\begin{align} &{{P}^{k+1}}={{P}^{k}}-\frac{1}{\delta }\left( {{X}^{k+1}}-{{X}^{k}} \right)-{{\Theta }^{\text{H}}}\left( \Theta {{X}^{k}}-Y \right) \\ &=\cdots =\sum\limits_{j=0}^{k}{{{\Theta }^{\text{H}}}}\left( Y-\Theta {{X}^{j}} \right)-\frac{1}{\delta }{{X}^{k+1}} \\ \end{align}$
(16) 令
${{V}^{k}}=\sum\limits_{j=0}^{k-1}{{{\Theta }^{\text{H}}}\left( Y-\Theta {{X}^{j}} \right)}$
(17) 可得
${{V}^{k+1}}={{V}^{k}}+{{\Theta }^{\rm H}}\left( Y-\Theta {{V}^{k}} \right) $
(18) 将 $J=\mu ||X|{{|}_{1}} $带入式(12)并忽略常数项得:
${{X}^{k+1}}=\text{arg}\underset{X\in {{C}^{N\times D}}}{\mathop{\text{min}}}\, \mu {{\left\| X \right\|}_{1}}+\frac{1}{2\delta }\left\| X-\delta \left( {{p}^{k}}+\Delta V+\frac{1}{\delta }{{X}^{k}} \right) \right\|_{\text{F}}^{2}$
(19) 其中, $\Delta V={{\Theta }^{\rm H}}\left( Y-\Theta {{X}^{k}} \right) $. 将 ${{\Theta }^{\rm H}}( Y-\Theta {{X}^{k}} )$ $={{V}^{k+1}}-{{V}^{k}} $及 ${{p}^{k}}={{V}^{k}}-{{X}^{k}}/{\delta } $ 代入式(19)得:
${{X}^{k+1}}=\text{arg}\underset{X\in {{C}^{N\times D}}}{\mathop{\text{min}}}\, \mu {{\left\| X \right\|}_{1}}+\frac{1}{2\delta }\left\| X-\delta {{V}^{k+1}} \right\|_{\text{F}}^{2}$
(20) 式(20)可用下式求解
${{X}^{k+1}}\text{ = sof}{{\text{t}}_{\mu }}({V}^{k+1}) $
(21) 结合式(18)和(21)即得PFLBI算法基本迭代格式, 此时完成了对式(7)的证明.
2.2 快速实现
由于LBI存在停滞现象, 式(7)也类似地存在停滞现象, 因此需要研究消除这一现象的方法. 文献[23]分析了LBI中停滞现象产生的原因: 即一次或几次中间变量的积累量不足以突破收缩阈值, 以至于这几次迭代时的输出保持不变. 为解决这一问题, 文献[23]提出利用改变迭代步长思想以消除实信号的停滞现象, 取得了较好的效果, 有效地加快了LBI的收敛速度. 本文将该思想用于在二维复信号重建以消除停滞现象, 下面进行具体分析.
消除停滞现象的重点在于估计V突破闭区间 $\left[-\mu , \mu \right] $需要的步长, 在停滞时间内, V的增量 $\Delta V\text{ = }{{\Theta }^{\rm H}}\left( Y-\Theta {{X}^{k}} \right) $可认为是固定的. 那么停滞期间的迭代过程可表示为
${{X}^{k+j}}\equiv {{X}^{k}}\ {{V}^{k+j}}\text{ = }{{V}^{k}}+j\Delta V, j=1, \cdots .$
(22) 为计算停滞步长, 首先对数据进行预处理. 对${{X}^{k}}$, ${{V}^{k}} $, ${{X}^{k+j}} $, ${{V}^{k+j}} $和 $\Delta V $分别进行矩阵向量化处理, 即${{\tilde{X}}^{k}}\text{ = vec}\left( {{X}^{k}} \right)$, ${{\tilde{V}}^{k}}\text{ = vec}\left( {{V}^{k}} \right)$, ${{\tilde{X}}^{k+j}}\text{ = vec}\left( {{X}^{k+j}} \right)$, ${{\tilde{V}}^{k+j}}\text{ = vec}\left( {{V}^{k+j}} \right)$和 $\Delta \tilde{V}\text{ = vec}\left( \Delta V \right)$.
定义 ${{I}_{0}} $为 ${{\tilde{X}}^{k}} $零元素的索引集, ${{I}_{1}}={{\bar{I}}_{0}} $为 ${{\tilde{X}}^{k}} $非零元素的支撑集, 此时式(22)可改写为如下分段形式:
$\tilde{X}_{i}^{k+j}=\tilde{X}_{i}^{k}, \forall i\ \tilde{V}_{i}^{k+j}=\tilde{V}_{i}^{k}+j\Delta {{\tilde{V}}_{i}}, i\in {{I}_{0}}\ \tilde{V}_{i}^{k+j}=\tilde{V}_{i}^{k}, i\in {{I}_{1}}.$
(23) 当且仅当 ${{I}_{0}} $中 ${{\tilde{V}}^{k}} $的元素突破闭区间 $\left[-\mu , \mu \right] $的限制时, ${{\tilde{X}}^{k}} $才会产生一个新的非零元素, 从而消除停滞现象. 当 $i\in {{I}_{0}}, \tilde{V}_{i}^{k}\in \left[-\mu , \mu \right] $时, 可以利用式(24)估计 $\tilde{V}_{i}^{k} $突破限制需要的积累步数, 即
$s\text{ = min}\left\{ {{s}_{i}} \right\}\text{=}\left\{ \left\lceil \frac{\mu \cdot \text{sgn}\left( \Delta {{{\tilde{V}}}_{i}} \right)-\tilde{V}_{i}^{k}}{\Delta {{{\tilde{V}}}_{i}}} \right\rceil , \forall i\in {{I}_{0}} \right\}$
(24) 其中, $\left\lceil \cdot \right\rceil $为取整符号, $s $即为需要的积累步数, 也就是停滞的长度. 得到 $s $后就可以利用式(25)终止停滞.
$\left\{ \begin{align} &{{X}^{k+s}}={{X}^{k}} \\ &{{V}^{k+s}}={{V}^{k}}+s\Delta V \\ \end{align} \right.\ $
(25) 因此, 当 ${{X}^{k}} $在两步迭代保持不变时, 认为其处于迭代停滞状态, 此时可通过增加 ${{V}^{k}} $的变化量以突破 $\left[-\mu , \mu \right] $, 从而使 ${{X}^{k}} $加速到停滞的临界点, 以此减少积累时间, 加快算法运行速度.
注意到, 本文方法能否较好地消除停滞现象主要取决于停滞状态 ${{X}^{k+s}}= {{X}^{k}}$的判断是否准确. 通常判断 ${{X}^{k+s}} = {{X}^{k}}$是利用两者之差小于一个较小的常数 $\varepsilon $, $\varepsilon $的取值不同会使算法的收敛速度不同: 若 $\varepsilon $的取值过小时, 则两步迭代的 ${{X}^{k}} $非常接近时, 算法才会估计迭代步长, 此时算法的收敛速度就较慢; 若 $\varepsilon $ 的取值较大时, 则两步迭代的 ${{X}^{k}} $相差较大时, 算法便会估计迭代步长, 此时算法的收敛速度就较快, 但是, 若 $\varepsilon $的取值过大, 算法会不收敛, 因此选择 $\varepsilon $时, 需要考虑在算法收敛的条件下, 选择较大的值, 来获得较快的收敛速度, 以减小停滞现象影响.
3. 算法性能分析
3.1 收敛性分析
对算法的收敛性进行分析时, 主要分析式(7)是否收敛, 因为PFLBI算法的输出序列是式(7)的子序列, 因此, 若式(7)收敛, 则PFLBI算法必收敛.
下面对式(7)的收敛性进行分析. 文献[24]给出了线性Bregman迭代的收敛性结论及证明, 该文中的线性Bregman迭代可认为是式(7)的特殊情况, 即实数向量形式, 描述为式(26).
$\left\{ \begin{align} &{{v}^{k+1}}={{v}^{k}}+{{\Theta }^{\text{H}}}(y-\Theta {{x}^{k}}) \\ &{{x}^{k+1}}=\delta \text{sof}{{\text{t}}_{\mu }}({{v}^{k+1}}) \\ \end{align} \right.\ $
(26) 将文献[24]对于式(26)的收敛性定理描述为定理1.
定理 1. 假设 $\Theta \in {R^{M\times N}} $是任意矩阵, $M\le N$, 且 $0<\delta <{1}/{\left\| \Theta {{\Theta }^{\rm T}} \right\|}$, 则由式(26)得到的序列 $\left\{ {{ x}^{k}} \right\} $收敛到式(27)的唯一解, 若 $\mu \to \infty $, 则序列 $\left\{ {{ x}^{k}} \right\} $的极限收敛于式(28)的一个最优解.
$\underset{ x\in {R^{N}}}{\mathop{\min }} \left\{ f( x) : x={\mathop{\arg}}\underset{ x\in {R^{N}}}{\mathop{\min }} g( x)\right\} $
(27) 其中, $f( x)=\mu {{\left\| x \right\|}_{1}}+{{\left\| x \right\|}^{2}}/{2\delta }$, $g( x)={{\left\| \Theta x-y \right\|}^{2}}$.
$\underset{ x\in {R^{N}}}{\mathop{\min }} \left\{ {{\left\| x \right\|}_{1}}: x={\mathop{\arg }}\underset{ x\in {R^{N}}}{\mathop{\min }} g( x) \right\} $
(28) 证明. 可将式(7)改写为如下形式:
$\left\{ \begin{align} &\left[ v_{1, \cdots , D}^{k+1} \right]=\left[ v_{1, \cdots , D}^{k} \right]+ \\ &{{\Theta }^{\text{H}}}\left( \left[ {{y}_{1, \cdots , D}} \right]-\Theta \left[ x_{1, \cdots , D}^{k} \right] \right) \\ &\ \left[ x_{1, \cdots , D}^{k+1} \right]=\delta \text{sof}{{\text{t}}_{\mu }}\left( \left[ v_{1, \cdots , D}^{k+1} \right] \right) \\ \end{align} \right.\ $
(29) 其中, $\left[v_{1, \cdots , D}^{k+1} \right]=\left[v_{1}^{k+1}, \cdots , v_{D}^{k+1} \right]$, $\left[x_{1, \cdots , D}^{k+1} \right]=\left[x_{1}^{k+1}, \cdots , x_{D}^{k+1} \right]$, $\left[y_{1, \cdots , D} \right]=\left[y_{1}, \cdots , y_{D} \right]$.
式(29)中的第 d 列为
$\left\{ \begin{align} &\left[ {{v}_{d}}^{k+1} \right]=\left[ {{v}_{d}}^{k} \right]+{{\Theta }^{\text{H}}}\left( \left[ {{y}_{d}} \right]-\Theta \left[ {{x}_{d}}^{k+1} \right] \right) \\ &\ \left[ {{x}_{d}}^{k+1} \right]=\delta \text{sof}{{\text{t}}_{\mu }}\left( \left[ {{v}_{d}}^{k+1} \right] \right) \\ \end{align} \right.$
(30) 实际中, 为保证运算速度, 算法处理时针对的是复数信号. 在分析收敛性时, 为方便分析, 可利用式(31)将复数转化为实数进行分析 [10].
$\eqalign{ &{x_d} = \left[ \matrix{ {\mathop{\rm Re}\nolimits} \left( {{x_d}} \right) \hfill \cr {\mathop{\rm Im}\nolimits} \left( {{x_d}} \right) \hfill \cr} \right], \Theta = \left[ {\matrix{ {{\mathop{\rm Re}\nolimits} \left( \Theta \right)}&{ - {\mathop{\rm Im}\nolimits} \left( \Theta \right)} \cr {\;{\mathop{\rm Im}\nolimits} \left( \Theta \right)}&{{\mathop{\rm Re}\nolimits} \left( \Theta \right)} \cr } } \right] \cr &{y_d} = \left[ \matrix{ {\mathop{\rm Re}\nolimits} \left( {{y_d}} \right) \hfill \cr \;{\mathop{\rm Im}\nolimits} \left( {{y_d}} \right) \hfill \cr} \right] \cr} $
(31) 转化为实数后, 式(30)满足定理1, 显然式(29)也满足定理1, 即式(7)满足定理1的收敛性结论, 又有PFLBI算法的输出序列是式(7)的子序列, 因此PFLBI算法也满足定理1的收敛性结论.
3.2 抗噪性分析
PFLBI算法的主体部分是式(7), 因此主要分析式(7). 为方便分析抗噪性能, 类似于文献[25], 将式(7)写为等价的式(32).
$\left\{ \matrix{ {Y^{k + 1}} = Y + {Y^k} - \Theta {X^k} \hfill \cr \;{X^{k + 1}} = \delta {{\mathop{\rm soft}\nolimits} _\mu }({\Theta ^{\rm{H}}}{Y^{k + 1}}) \hfill \cr} \right.$
(32) 噪声条件下, $Y=\Theta \bar{X}+\Omega$. 其中 $\bar{X} $为真实的无噪稀疏信号, 当 $\left\| Y-\Theta {{X}^{k}} \right\|\ge \left\| Y-\Theta \bar{X} \right\| $时, ${{X}^{k}} $依Bregman距离 $D_{J}^{{{p}^{k}}}\left( \bar{X}, {{X}^{k}} \right) $单调地趋向 $\bar{X}$. 当 $k=0$, ${{Y}^{0}}=0$, ${{X}^{0}}=0 $时, ${{Y}^{1}}=Y$, 将迭代(32)中的含噪量测输入 ${{Y}^{1}} $分解为两部分: ${{Y}^{1}}=\Theta {{X}^{1}}+\Theta {{B}^{1}}$, 其中 ${{X}^{1}} $ 可看作为原始纯净信号 $\bar{X} $的一部分, 因为 $\mu $取较大值时, 收缩算子 $\operatorname{soft} $可将 ${{\Theta }^{H}}{{Y}^{1}} $中的小信号成分过滤掉, 因此 ${{X}^{1}} $是过平滑的且不含任何噪声. ${{B}^{1}} $包含两部分: 1)原始纯净信号 $\bar{x} $中未恢复的信号 $\bar{X}-{{X}^{1}}$; 2)噪声分量 $\Omega $, 可表示为 $\Theta {{B}^{1}}=\Theta \left( \bar{X}-{{X}^{1}} \right)+\Omega $, 又有 ${{Y}^{1}}=\Theta {{X}^{1}}+\Theta {{B}^{1}}$, 所以 ${{Y}^{1}}=\Theta \left( \bar{X}-{{X}^{1}} \right)+\Omega +\Theta {{X}^{1}}$. 若期望从 ${{B}^{1}}$中恢复出未恢复信号 $\bar{X}-{{X}^{1}}$, 则需要在第二次迭代时将$\Theta {B}^{1}$反馈到原始含噪量测输入 Y中, 所以第二次迭代新的输入 ${{Y}^{2}}$为
$\eqalign{ &{Y^2} = Y + \Theta {B^1} = \cr &2\Theta {X^1} + 2\Theta {B^1} - \Theta {X^1} = \cr &2\Theta \left( {\bar X - {X^1}} \right) + 2\Omega + \Theta {X^1} \cr} $
(33) 与第一次迭代含噪量测输入 ${{Y}^{1}} $相比, 未恢复信号 $\bar{X}-{{X}^{1}} $变为两倍, 同时 ${{Y}^{2}} $包含的噪声分量也变为两倍. 由于第二次迭代新的含噪量测输入 ${{Y}^{2}} $可分解为 ${{Y}^{2}}=\Theta {{X}^{2}}+\Theta {{B}^{2}}$, 利用 ${{Y}^{2}} $求解 ${{X}^{2}} $时, ${{Y}^{2}} $中的信号成分不仅使 ${{X}^{2}} $继承了 ${{X}^{1}}$, 而且重建了未恢复信号 $\bar{X}-{{X}^{1}} $的部分信息, 因此 ${{X}^{2}} $ 比 ${{X}^{1}} $更逼近 $\bar{X}$. 若已知噪声方差 ${{\Sigma }^{2}}$, 则可以利用下式作为噪声条件下的停止准则:
$\left\| Y-\Theta {{X}^{k}} \right\|>\left\| Y-\Theta \bar{X} \right\|={{\Sigma }^{2}} $
(34) 3.3 计算复杂度分析
下面通过计算量分析比较算法的重建速度, 以一次加法或乘法为计算量单位.
首先分析式(7)的计算量, 一次迭代的计算量为 O$\left( D\left( 4MN+2N \right) \right)$, 假设经过 L 次循环得到最终解, 那么式(7)的计算量为 O$\left( DL\left( 4MN+2N \right) \right)$. PFLBI算法的计算量主要也是式(7)的迭代, 主要是迭代次数不同, 假设迭代 ${{L}_{1}}$ 次终止, 那么总的计算量为 O$\left( D{{L}_{1}}\left( 4MN+2N \right) \right)$. 由于PFLBI算法估计了停滞步长, 因此有 ${{L}_{1}}<L$. 因此, PFLBI算法比式(7)的计算量更小, 运算速度更快.
3.4 并行性分析
本文算法不同于传统的逐列重建, 而是整个矩阵同时重建, 即多列同时重建. 具有多个事件同时发生的思想, 因而具有并行性. 需要注意的是, 本文算法的并行性和计算机领域利用多部计算机同时处理的并行计算并不完全相同, 仅是思想相同. 下面进行具体分析.
首先将LBI拓展到二维复稀疏信号模型中, 实现直接对矩阵进行处理, 以及对二维复稀疏信号的并行重建. 此外, 体现本文算法并行性关键的一点是处理矩阵时, 将原始对向量收缩的软阈值算子改进为可直接对矩阵进行收缩的软阈值算子, 因而本文算法能够并行重建二维复稀疏信号.
4. 仿真与实验
这里首先通过仿真对算法的性能进行验证分析, 然后通过仿真数据及实测数据的ISAR成像进一步验证算法的性能与优势, 仿真中, 采用计算机语言为Matlab 语言, 计算机主要参数如下: 处理器为Intel酷睿E7500, 主频为2.93 GHz, 内存为2 GB.
4.1 算法性能验证与分析
仿真1. 可行性验证
本仿真主要验证本文算法对于已有复数模型算法的有效性, 因此重点与文献[8, 10]中的方法进行比较. 针对一般的复数信号, $ s=\left| a \right|{\rm exp} (i\theta )$, 其中 $a $幅度服从正态分布 $a\sim {\rm N}( 0, 1 )$, $\theta $服从均匀分布 $\theta \sim \operatorname{U}\left( -\pi , \pi \right)$, $ s $的长度为256, 稀疏度为10, 感知矩阵是 $128\times 256 $的随机高斯矩阵, 算法停止准则为 $\| \Theta {\hat{ s}}^{k}-{ s} \|_{2}/{\left\| s \right\|}_{2}\le 10^{-5}$, 最大迭代次数为5 000, 相对重建误差定义为: error$\text{ = }||{{\hat{ s}}^{k}}-s|{{|}_{2}}/|| s|{{|}_{2}}$. 仿真结果如图 2所示.
从图 2中可以看出, 文献[8, 10]的方法以及本文的PFLBI算法都能够有效地重建稀疏复信号的幅度和相位, 验证了本文算法的有效性.
仿真2. 收敛性验证 下面通过仿真对算法的收敛性进行验证, 仿真参数与仿真1相同, 相对重建误差的对数和迭代次数的变化关系如图 3所示.
从图 3可以看出, 式(7)和PFLBI算法的输出序列的相对重建误差随迭代次数的增加, 最终减小到设定的停止门限, 验证了PFLBI算法收敛性. 同时可看出式(7)存在停滞现象, PFLBI算法通过估计迭代步长的方法有效地消除了停滞, 减少了迭代次数, 加快了收敛速度, 体现出PFLBI算法的优势. 此外, 可以看出, 算法的收敛速度与 $\varepsilon $的取值有关, $\varepsilon $值越小, 则收敛速度越慢; $\varepsilon $值越大, 则收敛速度越快; 但 $\varepsilon $ 的取值过大时, 则算法不收敛, 仿真验证了理论分析的正确性.
仿真3. 抗噪性验证 本仿真主要考察PFLBI算法的重建精度对信噪比的敏感度, 并与文献[8]和文献[10]的方法进行比较, 仿真参数与仿真1相同, 噪声取复高斯白噪声, 信噪比的取值范围是[0 dB $\sim$ 35 dB], 步长为5, Monte Carlo仿真100 次. 图 4为相对重建误差与信噪比的关系.
由图 4可以看出, 在较低的信噪比下, 3种算法的相对重建误差都比较大, 都不能准确地重建出原始信号; 随着信噪比的增大, 3种算法的相对重建误差都越来越小. 可以看出本文PFLBI算法优于文献[8, 10]的方法.
仿真 4. 运算时间比较 本仿真主要验证PFLBI算法的速度优势, 仿真时与文献[8, 10]的方法进行比较. PFLBI算法停止准则及最大迭代次数与仿真1相同. 信号序列长度的取值范围是[256 $\sim$ 1 024], 步长为128, Monte Carlo仿真100次. 不同算法的运算时间关系如图 5所示.
由图 5可知, 随着信号序列长度的增加, 算法的运算时间都有所增加, 由于文献[8]的方法需要两次优化, 因此时间最长; 文献[10] 的方法需要将复数实数化, 增加了信号序列和感知矩阵的维度; 而本文算法能够直接处理复数信号, 所用时间较短, 验证了本文算法的优势.
4.2 仿真数据 ISAR 成像
为更好地验证本文算法的优势, 将所提算法应用于ISAR方位向成像. CS ISAR成像的核心思想是利用ISAR图像的稀疏性, 从少量回波中得到高分辨率甚至超分辨率图像. 文献[12, 26-27]已经对CS ISAR成像做了较为全面深入的研究, 本文算法应用于ISAR方位向成像的基础与这些文献相同, 这里就不再赘述. 文献[12, 26-27]中的CS ISAR方位向成像是逐个距离单元进行重建, 而本文方法是利用所提的PFLBI算法对所有距离单元同时重建, 达到并行处理的目的, 在保证成像质量的同时提高了成像效率. 仿真参数设置如下: 发射信号为线性调频(Linear frequency modulation, LFM)信号, 载频为10 GHz, 发射脉冲时宽10 $\mu$s, 信号带宽为400 MHz, 采样频率为800 MHz, 脉冲重复频率为200 Hz. 目标为34个散射点飞机模型, 假设飞机匀速飞行, 速度为300 m/s, 观测距离门参考位置50 km, 脉冲回波数为256个. 目标模型及脉压后结果如图 6所示.
为验证三种算法在不同信噪比下的有效性与成像效果, 分别与RD (Range dopler)算法和OMP (Orthogonal matching pursuit)算法成像结果比较. PFLBI算法中 $\delta ={1}/(2\left\| \Theta {{\Theta }^{\rm T}} \right\|)$, $\mu ={300}/{\delta }$. 图 7 (a)图 7(c) 分别为RD算法、OMP算法和PFLBI算法在不同信噪比条件下得到的ISAR成像仿真结果.
由图 7可知, 相比RD算法, 基于CS理论的三种重建算法得到的ISAR图像分辨率更高, 副瓣更低. 随着信噪比的降低, 三种算法的成像质量都有所下降: RD算法成像结果在低性噪比下受噪声影响严重; 由于利用噪声方差作为算法的停止准则, OMP算法和PFLBI算法受信噪比影响较小; 对比图像可知, PFLBI算法比OMP算法的成像结果副瓣更低, 虚假散射点更少, 验证了本文算法在不同信噪比下的良好成像性能.
4.3 实测数据 ISAR 成像
为更好地验证算法性能, 下面利用实测数据进行实验验证. 部分雷达参数如下: 雷达发射信号为LFM信号, 带宽为100 MHz, 工作频段为S波段, 脉冲重复频率为400 Hz, 回波脉冲数为1 570个. 实测数据不同信噪比的成像比较. PFLBI算法中 $\delta \text{ = }{1}/(2\left\| \Theta {{\Theta }^{\rm T}} \right\|)$, $\mu \text{ = }{300}/{\delta }$. 其中图 8为实测数据脉压后信噪比分别为14 dB、10 dB、6 dB、2 dB的结果, 图 9(a) $\sim$ (c) 分别为RD 算法、OMP算法和PFLBI算法在不同信噪比条件下得到的实测数据ISAR成像结果.
从图 9可以看出, 随着信噪比的降低, 三种算法的成像质量都有所下降, 都会出现丢失部分散射点信息及出现虚假散射点的情况: 其中RD算法分辨率较低, 成像结果受噪声影响严重, 低信噪比时出现大量虚假散射点; OMP算法和PFLBI算法提高了分辨率, 降低了副瓣, 受信噪比影响较小, 但PFLBI算法成像结果优于OMP算法, 副瓣更低, 虚假散射点更少. 实测数据进一步验证了PFLBI算法在不同信噪比下的良好成像性能.
5. 结论
本文针对重建二维复信号时, 出现的存储空间和计算复杂度增加的问题, 首先, 构建了任意稀疏结构的二维复稀疏信号模型. 然后, 基于LBI构建了PFLBI算法基本迭代格式, 同时利用估计迭代步长的方法加快了收敛过程, 提出了PFLBI算法. 理论和仿真分析表明, PFLBI算法具有良好的收敛性、抗噪性和重建二维复稀疏信号时速度的优势, 同时, PFLBI算法能够有效消除停滞现象, 提高运算效率. 最后, 将PFLBI算法应用于ISAR成像, 不同信噪比的仿真及实测数据成像结果验证了PFLBI算法的良好性能.
-
图 2 两尺度径向基小波核LS-SVM的实验结果
Fig. 2 Experimental results of two-scale RBF wavelet kernel LS-SVM
图 3 标准LS-SVM、稀疏LS-SVM、两尺度LS-SVM、稀 疏两尺度LS-SVM 四算法在不同稀疏度下NMSE 比较
Fig. 3 NMSE comparison of standard LS-SVM, sparse LS-SVM, two-scale LS-SVM, sparse two-scale LS-SVM algorithms under di®erent sparse degrees
图 4 标准LS-SVM和两尺度LS-SVM的回归结果比较
Fig. 4 Regression results comparison of standard LS-SVM and two-scale LS-SVM
图 6 90% 稀疏度两尺度LS-SVM 逼近效果
Fig. 6 Approximation result of 90% sparse degree two-scale LS-SVM
图 7 90% 稀疏度标准LS-SVM 逼近效果
Fig. 7 Approximation result of 90% sparse degree standard LS-SV
图 8 标准LS-SVM 和两尺度LS-SVM 在50% 稀疏度下拟合结果比较
Fig. 8 Approximation results comparison of standard LS-SVM and two-scale LS-SVM under 50% sparse degree
图 9 标准LS-SVM 和两尺度LS-SVM 在不同稀疏度下 NMSE 比较
Fig. 9 NMSE comparison of standard LS-SVM and two-scale LS-SVM under di®erent sparse degrees
图 11 标准LS-SVM、稀疏LS-SVM、两尺度LS-SVM、稀 疏两尺度LS-SVM 四算法在不同稀疏度下NMSE 比较
Fig. 11 NMSE comparison of standard LS-SVM, sparse LS-SVM, two-scale LS-SVM, sparse two-scale LS-SVM algorithms under di®erent sparse degrees
图 12 标准LS-SVM 和两尺度LS-SVM 在50% 稀疏度下的拟合结果比较
Fig. 12 Approximation results comparison of standard LS-SVM and two-scale LS-SVM under 50% sparse degree
表 1 不同小波核函数的两尺度LS-SVM NMSE 比较
Table 1 NMSE comparison of two-scale LS-SVM with di®erent wavelet kernel functions
核函数 参数选择 准确率(NMSE) RBF 小波核 $\gamma_1=50, \gamma_2=100, \sigma_1^2=0.5, \sigma_2^2=3.5$ -47.1780 Morlet 小波核 $\gamma_1=80, \gamma_2=150, \sigma_1^2=0.8, \sigma_2^2=4$ -46.4707 Mexican hat 小波核 $\gamma_1=100, \gamma_2=200, \sigma_1^2=0.35, \sigma_2^2=6.25$ -46.6829 
下载: 导出CSV
表 2 不同核函数的两尺度LS-SVM NMSE 比较
Table 2 NMSE comparison of two-scale LS-SVM with di®erent kernel functions
核函数 参数选择 准确率(NMSE) RBF 小波核 $\gamma_1=50, \gamma_2=100, \sigma_1^2=0.5, \sigma_2^2=3.5$ -47.1780 RBF 核 $\gamma_1=100, \gamma_2=200, \sigma_1^2=0.3, \sigma_2^2=3$ -44.7617 Sinc 小波核 $\gamma_1=60, \gamma_2=220, \sigma_1^2=0.5, \sigma_2^2=5$ -44.1170
下载: 导出CSV
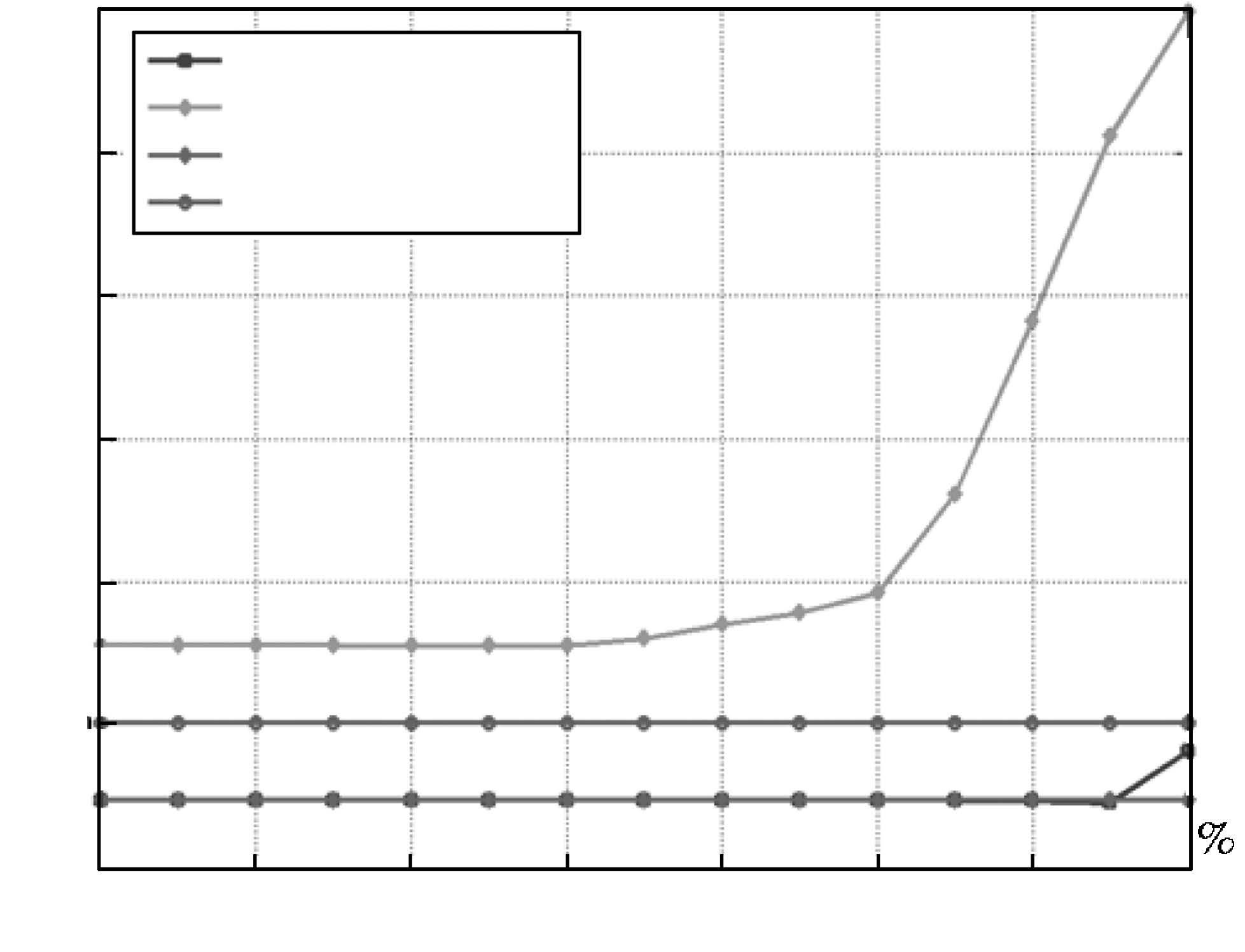
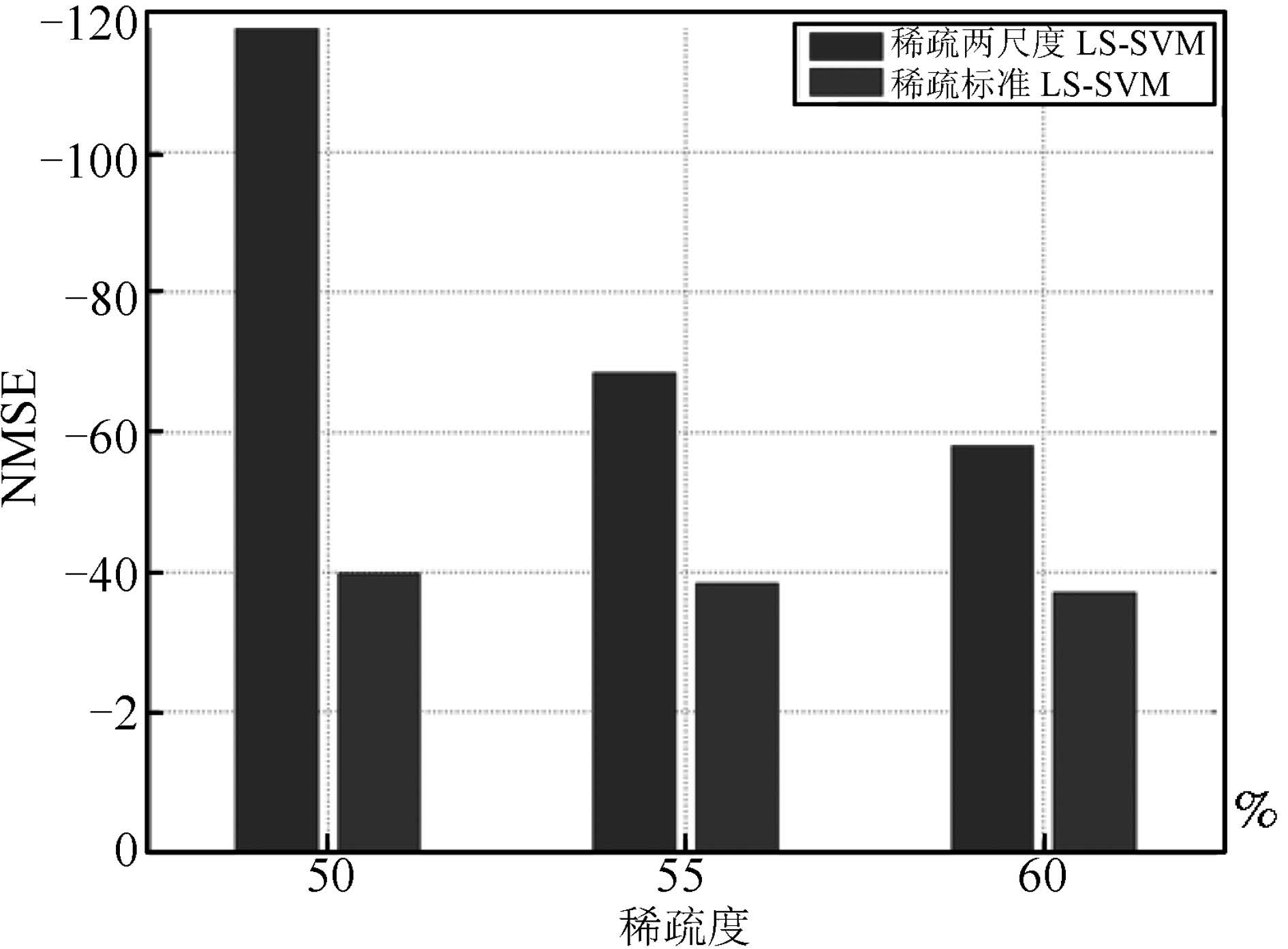
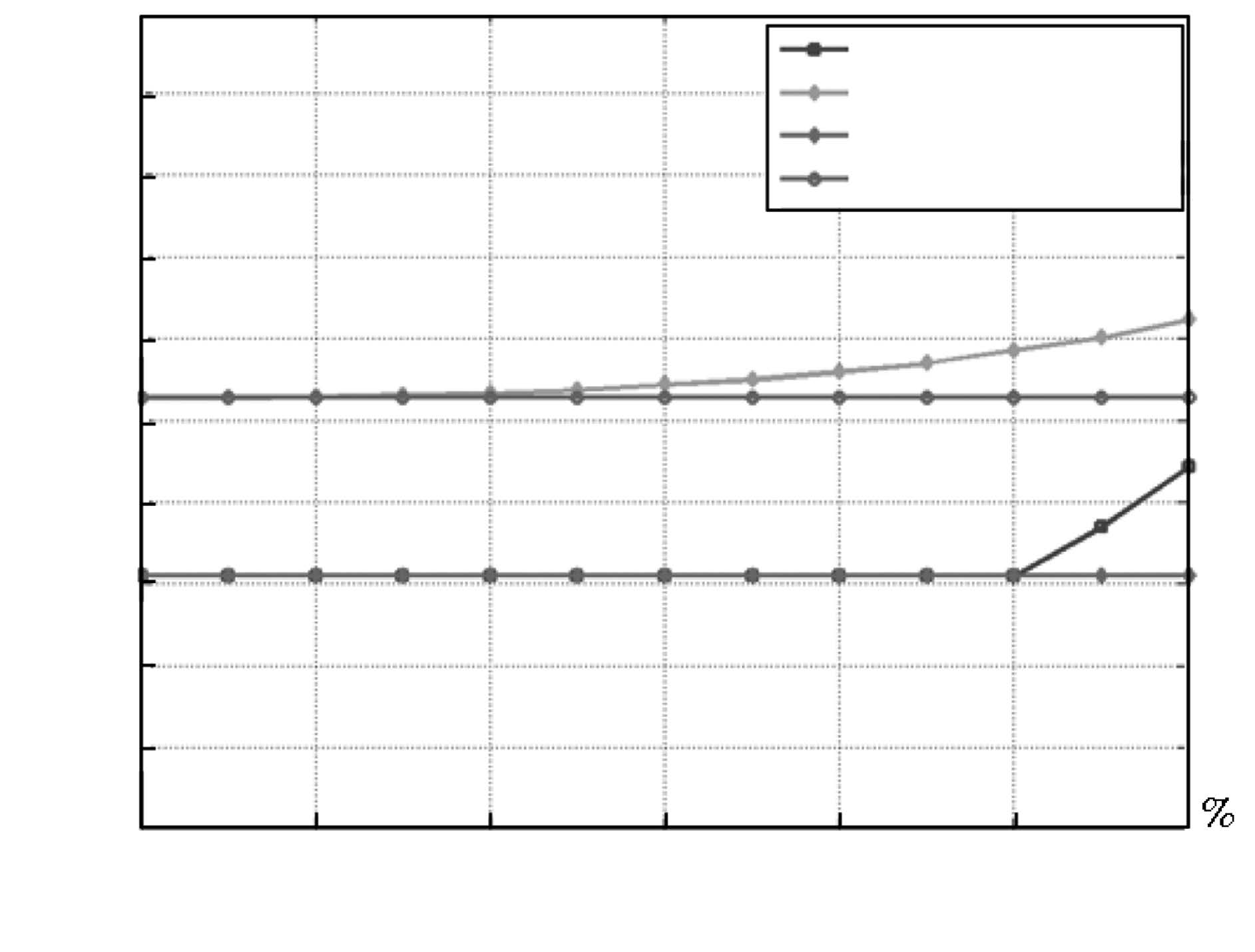
表 4 稀疏两尺度LS-SVM 和稀疏标准LS-SVM 在不同稀疏度下NMSE 比较
Table 4 NMSE comparison of sparse two-scale LS-SVM and sparse standard LS-SVM algorithms under di®erent sparse degrees
稀疏度(%) 90 80 70 60 50 40 30 20 10 NMSE 两尺度 -52.8800 -59.7540 -69.7735 -72.7535 -72.9664 -72.9800 -72.9805 -72.9805 -72.9805 标准 -49.9373 -54.9217 -58.7773 -63.1308 -64.8218 -65.3600 -65.4205 -65.4312 -65.4312
下载: 导出CSV
-
[1] Vapnik V N. The Nature of Statistical Learning Theory. New York: Springer-Verlag, 1995. 69-83 http://www.oalib.com/references/16885293 [2] Suykens J A K, Vandewalle J. Least squares support vector machine classifiers. Neural Processing Letters, 1999, 9(3): 293-300 doi: 10.1023/A:1018628609742 [3] Zhao H B, Ru Z L, Chang X, Yin S D, Li S J. Reliability analysis of tunnel using least square support vector machine. Tunnelling and Underground Space Technology, 2014, 41: 14-23 doi: 10.1016/j.tust.2013.11.004 [4] Esfahani S, Baselizadeh S, Hemmati-Sarapardeh A. On determination of natural gas density: least square support vector machine modeling approach. Journal of Natural Gas Science and Engineering, 2015, 22: 348-358 doi: 10.1016/j.jngse.2014.12.003 [5] Yang J, Bouzerdoum A, Phung S L. A training algorithm for sparse LS-SVM using compressive sampling. In: Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing. Dallas, TX, USA: IEEE, 2010. 2054-2057 [6] Zhang L, Zhou W D, Jiao L C. Wavelet support vector machine. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 2004, 34(1): 34-39 doi: 10.1109/TSMCB.2003.811113 [7] 沈燕飞, 李锦涛, 朱珍民, 张勇东, 代锋. 基于非局部相似模型的压缩感知图像恢复算法. 自动化学报, 2015, 41(2): 261-272 http://www.aas.net.cn/CN/abstract/abstract18605.shtmlShen Yan-Fei, Li Jin-Tao, Zhu Zhen-Min, Zhang Yong-Dong, Dai Feng. Image reconstruction algorithm of compressed sensing based on nonlocal similarity model. Acta Automatica Sinica, 2015, 41(2): 261-272 http://www.aas.net.cn/CN/abstract/abstract18605.shtml [8] Mallat S G. A Wavelet Tour of Signal Processing. Sam Diego: Academic Press, 1998. [9] Zhao J X, Song R F, Zhao J, Zhu W P. New conditions for uniformly recovering sparse signals via orthogonal matching pursuit. Signal Processing, 2015, 106: 106-113 doi: 10.1016/j.sigpro.2014.06.010 [10] Elad M. Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing. New York: Springer-Verlag, 2010. http://www.oalib.com/references/16302471 [11] Yang L, Han J Q, Chen D K. Identification of nonlinear systems using multi-scale wavelet support vectors machines. In: Proceedings of the 2007 IEEE International Conference on Control and Automation. Guangzhou, China: IEEE, 2007. 1779-1784 [12] Yang L X, Yang S Y, Zhang R, Jin H H. Sparse least square support vector machine via coupled compressive pruning. Neurocomputing, 2014, 131: 77-86 doi: 10.1016/j.neucom.2013.10.038 [13] Schniter P, Potter L C, Ziniel J. Fast Bayesian matching pursuit. In: Proceedings of the 2008 Information Theory and Applications Workshop. San Diego, CA, USA: IEEE, 2008. 326-333 [14] Zhang Y P, Sun J G. Multikernel semiparametric linear programming support vector regression. Expert Systems with Applications, 2011, 38(3): 1611-1618 doi: 10.1016/j.eswa.2010.07.082 [15] 赵永平, 孙建国. 一类非平坦函数的多核最小二乘支持向量机的鲁棒回归算法. 信息与控制, 2008, 37(2): 160-165 http://www.cnki.com.cn/Article/CJFDTOTAL-XXYK200802007.htmZhao Yong-Ping, Sun Jian-Guo. A non-flat function robust regression algorithm using multi-kernel LS-SVM. Information and Control, 2008, 37(2): 160-165 http://www.cnki.com.cn/Article/CJFDTOTAL-XXYK200802007.htm [16] Cai Y N, Wang H Q, Ye X M, Fan Q G. A multiple-kernel LSSVR method for separable nonlinear system identification. Journal of Control Theory and Applications, 2013, 11(4): 651-655 doi: 10.1007/s11768-013-2035-9 [17] Balasundaram S, Gupta D, Kapil. Lagrangian support vector regression via unconstrained convex minimization. Neural Networks, 2014, 51: 67-79 doi: 10.1016/j.neunet.2013.12.003 期刊类型引用(2)
1. 冯俊杰, 张弓. 多测量向量块稀疏信号重构ISAR成像算法. 系统工程与电子技术. 2017(09): 1959-1964 . 
百度学术2. 王智文. 二维条形码在医疗设备管理中的应用价值. 临床医学研究与实践. 2017(03): 185-186 . 百度学术其他类型引用(0)
-
下载:
计量
- 文章访问数: 2422
- HTML全文浏览量: 231
- PDF下载量: 1085
- 被引次数: 2
