-
摘要: 研究了状态依赖广义时变脉冲系统的时域稳定问题.基于微分矩阵不等式 (Differential matrix inequalities, DMI) 和S-procedure理论, 给出了两类状态依赖广义时变脉冲系统时域稳定的充分条件.接下来, 根据给出的充分条件设计了状态反馈控制器, 使得闭环系统时域稳定.最后, 给出数值算例来验证结论的有效性.Abstract: This paper deals with the state-dependent finite-time stability problem for continuous-time linear time-varying descriptor impulse systems. The sufficient conditions for state-dependent continuous-time linear time-varying descriptor impulse systems to be finite-time stable are proposed in terms of a set of differential matrix inequalities (DMI) and the S-procedure arguments. Based on the conditions above, a state feedback controller is designed such that the resultant closed-loop system is finite-time stable. Finally, an example is presented to show the effectiveness of the obtained theoretical results.
-
广义系统[1]的研究是从20世纪70年代[2]开始的, 在近40年的历史中广义系统理论研究得到了迅速发展, 并取得了一系列的丰硕成果[3-5].广义系统理论已成为现代控制理论中一个独立的研究领域, 这些研究成果主要集中在广义定常系统[6]、广义周期时变系统[7-8]和广义时变系统[9-10].随着科学技术的发展和工程技术的需要, 广义时变系统时域控制研究也受到了广泛的关注.
时域稳定性最早是由Kamenkov在文献[11]中提出来的, 至今已有很多可观的成果.文献[12-15]提出了时域稳定和时域有界的定义, 并对一般线性时变系统的时域稳定进行研究.文献[16-18]给出了带脉冲的线性时变系统的时域稳定的定义, 并利用 $L_{2}$ 增益给出时域稳定的判定定理.文献[19-22]探讨了带有干扰的参数不确定性系统时域稳定及时域控制的问题, 文献[23-24]利用微分矩阵不等式研究了一类带有跳变的线性时变系统的时域稳定. Ambrosino等研究了状态依赖时变脉冲动力系统的时域稳定性问题[25], 并在文献[26-29]中对时间依赖和状态依赖脉冲动力系统的时域稳定进行了对比和分析.文献[30-31]利用分段线性化将时变矩阵转化为一组标准的矩阵不等式, 解决了小区间内时变矩阵不等式的求解问题.时变脉冲系统中的研究方法多是时变系统与正常脉冲系统的自然推广, 文中所研究的广义时变脉冲系统不仅是时变脉冲系统的推广, 而且还考虑到广义系统自身的脉冲效应, 因此给研究和实验带来了一定的困难.
本文主要研究状态依赖广义时变脉冲系统的时域稳定问题.在考虑广义系统自身无脉冲效应的前提下, 运用微分矩阵不等式方法给出了广义时变脉冲系统时域稳定的充分条件, 并设计了状态反馈控制器.最后根据分段线性化将小区间内广义时变矩阵不等式转化为广义时不变线性矩阵不等式, 应用Matlab LMI工具箱编程进行求解.
1. 问题描述
$\boldsymbol{R} ^{n}$ 表示 $n$ -维欧几里得空间, $\boldsymbol{R}^{+}$ 是正实数集, $R > 0$ 是对称正定矩阵. ${N}$ 是自然数. $J=[t_0, t_0 +T]$ 表示时间域, 其中, $T \in \boldsymbol{R}^{+}$ .
考虑如下形式的状态依赖广义时变脉冲系统:
$ \begin{align} \left\{ \begin{array}{l} E\dot{{\boldsymbol x}}(t)=A(t){\boldsymbol x}(t), \quad {\boldsymbol x}(t)\notin \mathcal{S}_k\\ {\boldsymbol x}^{+}_{k}(t)=A_{d, k}{\boldsymbol x}(t), \quad {\boldsymbol x}(t)\in \mathcal{S}_k\\ {\boldsymbol x}(t_{0})={\boldsymbol x}_{0}, \quad k=1, 2, \cdot\cdot\cdot, N \end{array} \right. \end{align} $
(1) 其中, ${\boldsymbol x}(t)\in \boldsymbol{R}^{n}$ 为状态向量; $A(\cdot):t\in \boldsymbol{R}^{+}\mapsto \boldsymbol{R}^{n\times n}$ 是连续的函数矩阵, $A_{d, k}\in \boldsymbol{R}^{n\times n}, k=1, 2, \cdot\cdot\cdot, {N} $ 是时不变矩阵; $E$ 为奇异矩阵; ${S}_{k}\subseteq \boldsymbol{R}^{n}, k=1, 2, \cdot\cdot\cdot, {N}$ 是单连通互不相交的跳变集合 $({\boldsymbol x}_{0}\notin \mathcal{S}_{k})$ .根据脉冲时刻定义如下跳变时间集合:
$ \mathcal{T}_{x(\cdot)}=\{t\in \boldsymbol{R}^{+}|{\boldsymbol x}(t)\in \mathcal{S}_{k}, k=1, 2, \cdot\cdot\cdot, {N}\} $
定义1.如果 ${\boldsymbol x}_{0}^{\rm T}E^{\rm T}R{\boldsymbol x}_{0}\leq c_{1}$ 推出 ${\boldsymbol x}^{\rm T}(t)E^{\rm T}\Gamma(t){\boldsymbol x}(t) < c_{1}$ , 对 $\forall t\in J$ , 则称系统 (1) 是对于 $(c_1, J, R, \Gamma(\cdot))$ 时域稳定的.其中 $c_{1}>0, R$ 是对称正定矩阵, $\Gamma(\cdot)$ 是定义在 $J$ 上的函数矩阵, $\Gamma(t_0) < R$ .
定义2.如果存在常数 $s$ 对于任意 $t\in J$ 使得 $\det (sE-A(t)) \neq 0$ , 则广义时变系统 $E\dot{{\boldsymbol x}}(t)=A(t){\boldsymbol x}(t)$ 是一致正则的.
系统 (1) 一致正则与Campbell意义下的解析可解是等价的, 广义时变系统的一致正则性和 $A(t)$ 的连续性保证了其解的存在唯一性, 下面的讨论假定系统是一致正则的.我们将系统作如下分解:
$ \begin{align*} &MEN\!=\!\left[\begin{array}{ccc} I&0\\0&0 \end{array}\right], MA(t)N\!=\!\left[\begin{array}{ccc} A_{11}(t)& A_{12}(t)\\A_{21}(t)& A_{22}(t)\end{array}\right]\\ &N^{-1}{\boldsymbol x}(t)=\left[\begin{array}{ccc}{\boldsymbol x}_{1}(t)& {\boldsymbol x}_{2}(t)\end{array}\right]\end{align*} $
其中, $M, N$ 均为可逆矩阵, 则系统 (1) 等价于如下系统:
$ \begin{align*} \begin{aligned} &\dot{{\boldsymbol x}}_{1}(t)=A_{11}(t){\boldsymbol x}_{1}(t)+A_{12}(t) {\boldsymbol x}_{2}(t)\\ &0 = A_{21}(t) {\boldsymbol x}_{1}(t)+A_{22}(t){\boldsymbol x}_{2}(t) \end{aligned} \end{align*} $
显然, 系统 (1) 对于任意初始条件无脉冲的充要条件是 $A_{22}(t)$ 可逆.
另外考虑一类带有外部干扰的状态依赖广义时变脉冲系统
$ \begin{align} \left\{ \begin{array}{l} E\dot{{\boldsymbol x}}(t)=A(t){\boldsymbol x}(t)+G(t){\boldsymbol\omega}(t), \quad {\boldsymbol x}(t)\notin \mathcal{S}_k\\ {\boldsymbol x}^{+}_{k}(t)=A_{d, k}{\boldsymbol x}(t), \quad {\boldsymbol x}(t)\in \mathcal{S}_k\\ {\boldsymbol x}(t_{0})={\boldsymbol x}_{0}, \quad k=1, 2, \cdot\cdot\cdot, {N} \end{array} \right. \end{align} $
(2) 外部干扰 ${\boldsymbol \omega}(t)$ 满足:
$ \begin{align} \begin{array}{l} \int_{t_0}^{t_0 +T}{\boldsymbol \omega}^{\rm T}(s){\boldsymbol \omega}(s){\rm d}s\leq d, \quad d\geq 0 \end{array} \end{align} $
(3) 定义3.如果 ${\boldsymbol x}_{0}^{\rm T}E^{\rm T}R{\boldsymbol x}_{0}\leq c_{1}$ 推出 ${{\boldsymbol{x}}^{\text{T}}}(t){{E}^{\text{T}}}\Gamma (t)\boldsymbol{x}(t) < {{c}_{2}}$ , 对 $\forall t\in J$ , 则称系统 (2) 是对于 $(c_1, c_2, {\boldsymbol \omega(t)}, J, R, \Gamma(\cdot))$ 时域稳定的.其中 $0 < c_{1} < c_{2}, R$ 是对称正定矩阵, $\Gamma(\cdot)$ 是定义在 $J$ 上的函数矩阵, $\Gamma(t_0) < R$ , 外部干扰 ${\boldsymbol \omega}(t)$ 满足式 (3).
2. 时域稳定性分析
本节分别对系统 (1) 和 (2) 给出时域稳定的充分条件.
定理1.对于系统 (1), 如果存在分段连续可微对称非奇异函数矩阵 $P(\cdot)$ 在 $J$ 上满足下列一组矩阵不等式, $\forall t\in J$ .
$ E^{\rm T}P(t)=P^{\rm T}(t)E\geq 0 $
(4a) $ A^{\rm T}(t)P(t)+P^{\rm T}(t)A(t)+E^{\rm T}\dot{P}(t) < 0 $
(4b) $ \begin{array}{l} A_{d, k}^{\rm T}E^{\rm T}P(t)A_{d, k}-E^{\rm T}P(t) < 0\\ \qquad {\boldsymbol x}(t)\in \mathcal{S}_k, \qquad k=1, 2, \cdot\cdot\cdot, {N} \end{array} $
(4c) $ E^{\rm T}\Gamma(t)\leq E^{\rm T}P(t)\leq E^{\rm T}P(t_0) < E^{\rm T}R $
(4d) 则称系统 (1) 对于 $(c_1, J, R, \Gamma(\cdot))$ 时域稳定.
证明. 由定理条件 (4a) 和下式
$ \begin{align*} M^{\rm -T}P(t)N=\left[\begin{array}{cc}P_{1}(t)&P_{2}(t)\\ P_{3}(t)&P_{4}(t)\end{array}\right] \end{align*} $
有 $P_2(t)=0$ 和 $P_1(t)$ 对称, 将条件 (4b) 进行分解可得:
$ \begin{align*} \begin{aligned} &N^{\rm T}A^{\rm T}(t)M^{\rm T}M^{\rm -T}P(t)N +\\ &\quad N^{\rm T}P^{\rm T}(t)M^{-1}MA(t)N+\\ &\quad N^{\rm T}E^{\rm T}M^{\rm T}M^{\rm -T}\dot{P}(t)N =\\ &\quad \left[\begin{array}{cc}A_{11}^{\rm T}(t)&A_{21}^{\rm T}(t)\\A_{12}^{\rm T}(t)&A_{22}^{\rm T}(t)\end{array}\right]\left[\begin{array}{cc}P_{1}(t)&P_{2}(t)\\P_{3}(t)&P_{4}(t)\end{array}\right]+\\ &\quad \left[\begin{array}{cc}P_{1}^{\rm T}(t)&P_{3}^{\rm T}(t)\\P_{2}^{\rm T}(t)&P_{4}^{\rm T}(t)\end{array}\right]\left[\begin{array}{cc}A_{11}(t)&A_{12}(t)\\A_{21}(t)&A_{22}(t)\end{array}\right]+\\ &\quad \left[\begin{array}{cc}I&0\\0&0\end{array}\right]\left[\begin{array}{cc}\dot{P}_{1}(t)&\dot{P}_{2}(t)\\ \dot{P}_{3}(t)&\dot{P}_{4}(t)\end{array}\right]=\\ &\quad \left[\begin{array}{cc}\ast&\ast\\\ast&A_{22}^{\rm T}(t)P_{4}(t)+P_{4}^{\rm T}(t)A_{22}(t)\end{array}\right] < 0 \end{aligned} \end{align*} $
由上式显然有 $A_{22}^{\rm T}(t)P_{4}(t)+P_{4}^{\rm T}(t)A_{22}(t) < 0$ .因此, $A_{22}(t)$ 可逆, 系统对任意初始状态无脉冲.
构造下列广义Lyapunov函数
$ \begin{align*} V(t, {\boldsymbol x})={\boldsymbol x}^{\rm T}(t)E^{\rm T}P(t){\boldsymbol x}(t) \end{align*} $
当 $t\notin \mathcal{T}_{x(\cdot)}$ , 即系统状态向量 ${\boldsymbol x}(t)$ 没有达到跳变集合.则对 $V(t, {\boldsymbol x})$ 求导:
$ \begin{align*} &\dot V(t, {\boldsymbol x})={\boldsymbol x}^{\rm T}(t)[A^{\rm T}(t)P(t)+P^{\rm T}(t)A(t)+\\ &\qquad E^{\rm T}\dot{P}(t)]{\boldsymbol x}(t) \end{align*} $
由条件 (4b) 可知 $\dot V(t, {\boldsymbol x})< 0$ .
然而当 $t\in\mathcal{T}_{x(\cdot)}$ , 即系统依赖状态发生跳变, 由条件 (4c) 可得:
$ \begin{align*} & V (t, {\boldsymbol x}^+_k)-V (t, {\boldsymbol x})={\boldsymbol x}^{\rm T}(t)\times\\ & \qquad [A_{d, k}^{\rm T}E^{\rm T}P (t) A_{d, k}-E^{\rm T}P (t)]{\boldsymbol x}(t) < 0 \end{align*} $
则可以推出 $V(t, {\boldsymbol x})$ 在 $J$ 上是严格递减的.
对于系统 (1) 给定初始条件 $t_0$ 使得 ${\boldsymbol x}_{0}^{\rm T}E^{\rm T}R{\boldsymbol x}_{0}\leq c_{1}$ , 对所有的 $t\in J$ 都有:
$ \begin{align*} \begin{aligned} {\boldsymbol x}^{\rm T}(t)E^{\rm T}\Gamma(t){\boldsymbol x}(t)&\leq {\boldsymbol x}^{\rm T}(t)E^{\rm T}P(t){\boldsymbol x}(t)\leq\\ & {\boldsymbol x}_{0}^{\rm T}E^{\rm T}P(t_0){\boldsymbol x}_{0} < \\ &{\boldsymbol x}_{0}^{\rm T}E^{\rm T}RE{\boldsymbol x}_{0} < c_1 \end{aligned} \end{align*} $
因此系统 (1) 对于 $(c_1, J, R, \Gamma(\cdot))$ 时域稳定.
定理2.对于系统 (2), 如果存在分段连续可微对称非奇异函数矩阵 $P(\cdot)$ 在 $J$ 上满足下列不等式, $\forall t\in J$ .
$ E^{\rm T}P(t)=P^{\rm T}(t)E\geq 0 $
(5a) $ \begin{bmatrix} \Pi(t)&P^{\rm T}(t)G(t)\\ G^{\rm T}(t)P(t)&-I \end{bmatrix}< 0 $
(5b) $ \begin{array}{l} A_{d, k}^{\rm T}E^{\rm T}P(t)A_{d, k}-E^{\rm T}P(t)< 0\\ \qquad {\boldsymbol x}(t)\in \mathcal{S}_k, \qquad k=1, 2, \cdot\cdot\cdot, {N} \end{array} $
(5c) $ E^{\rm T}\Gamma(t)\leq E^{\rm T}P(t)\leq E^{\rm T}P(t_0) < E^{\rm T}R $
(5d) 则称系统 (2) 是对于 $(c_1, c_2, {\boldsymbol \omega}(t), J, R, \Gamma(\cdot))$ 时域稳定的.其中
$ \begin{align*} \Pi(t)=A^{\rm T}(t)P(t)+P^{\rm T}(t)A(t)+E^{\rm T}\dot{P}(t) \end{align*} $
证明.由条件 (5b) 可知 $\Pi(t) < 0$ , 同理可证系统 (2) 对任意初始状态无脉冲.
考虑下列广义Lyapunov函数
$ \begin{align*} V(t, {\boldsymbol x})={\boldsymbol x}^{\rm T}(t)E^{\rm T}P(t){\boldsymbol x}(t) \end{align*} $
当 $t\notin \mathcal{T}_{x(\cdot)}$ , 即系统状态向量 ${\boldsymbol x}(t)$ 没有达到跳变集合.则对 $V(t, {\boldsymbol x})$ 求导:
$ \begin{align*} \begin{array}{l} \dot V(t, {\boldsymbol x})={\boldsymbol x}^{\rm T}(t)\Pi(t){\boldsymbol x}(t)+{\boldsymbol \omega}^{\rm T}(t)G^{\rm T}(t)P(t)\times\\ {\boldsymbol x}(t)+{\boldsymbol x}^{\rm T}(t)P^{\rm T}(t)G(t){\boldsymbol \omega}(t) \end{array} \end{align*} $
构造下列向量
$ \begin{align*} {\boldsymbol z}(t)=\left[\begin{array}{c}{\boldsymbol x}(t)\\ {\boldsymbol \omega}(t) \end{array}\right] \end{align*} $
由式 (5b) 得:
$ \begin{array}{lll} {\boldsymbol z}^{\rm T}(t) \left[\begin{array}{cc}\Pi(t)&P^{\rm T}(t)G(t)\\ G^{\rm T}(t)P(t)&-I\end{array}\right]{\boldsymbol z}(t)=\\ \quad \dot V(t, {\boldsymbol x})-{\boldsymbol \omega}^{\rm T}(t){\boldsymbol \omega}(t) < 0 \end{array} $
显然有:
$ \begin{align*} \dot V(t, {\boldsymbol x}) < {\boldsymbol \omega}^{\rm T}(t){\boldsymbol \omega}(t) \end{align*} $
对上式在 $[t_0, t]$ 上求积分得:
$ \begin{align*} \int_{t_0}^{t}\dot V(s, {\boldsymbol x}){\rm d}s < \int_{t_0}^{t}{\boldsymbol \omega}^{\rm T}(s){\boldsymbol \omega}(s){\rm d}s \end{align*} $
则
$ \begin{align*} \begin{aligned} V(t, {\boldsymbol x})& < V(t_0, {\boldsymbol x})+\int_{t_0}^{t}{\boldsymbol \omega}^{\rm T}(s){\boldsymbol \omega}(s){\rm d}s < \\ &{\boldsymbol x}_{0}^{\rm T}E^{\rm T}P(t_0){\boldsymbol x}_{0}+d < \\ &{\boldsymbol x}_{0}^{\rm T}E^{\rm T}R{\boldsymbol x}_{0}+d < \\ &c_1+d \end{aligned} \end{align*} $
当 $t\in\mathcal{T}_{x(\cdot)}$ , 即系统状态发生跳变
$ \begin{align*} \begin{aligned} V(t, {\boldsymbol x}^+)&= {\boldsymbol x}^{\rm T}(t)A_{d, k}^{\rm T}E^{\rm T}P(t)A_{d, k}{\boldsymbol x}(t)< \\ &{\boldsymbol x}^{\rm T}(t)E^{\rm T}P(t){\boldsymbol x}(t) < V(t, {\boldsymbol x}) < \\ &c_1+d \end{aligned} \end{align*} $
则 $\exists c_2>c_1$ 使得 $V(t, {\boldsymbol x})$ 在 $J$ 上有 $V(t, {\boldsymbol x}) < c_2$ .
对系统 (2) 给定初始条件 $t_0$ 使得 ${\boldsymbol x}_{0}^{\rm T}E^{\rm T}R{\boldsymbol x}_{0}\leq c_{1}$ , 对所有的 $t\in J$ 都有:
$ \begin{align*} {\boldsymbol x}^{\rm T}(t)E^{\rm T}\Gamma (t){\boldsymbol x}(t)\leq {\boldsymbol x}^{\rm T}(t)E^{\rm T}P(t){\boldsymbol x}(t) < c_2\end{align*} $
则称系统 (2) 对于 $(c_1, c_2, {\boldsymbol\omega}(t), J, R, \Gamma(\cdot))$ 时域稳定.
接下来应用S-procedure理论[30]进一步研究系统 (1) 和系统 (2) 的时域稳定.
引理1[25].存在一个连续闭集 $\mathcal{S}\subseteq \boldsymbol{R}^n$ 、对称矩阵 $Q_0\in \boldsymbol{R}^{n\times n}$ 、 $Q_i\in \boldsymbol{R}^{n\times n}$ 满足:
$ {\boldsymbol x}^{\rm T}(t)Q_{0}{\boldsymbol x}(t) < 0, \quad {\boldsymbol x}(t)\in \mathcal{S} $
(6a) $ {\boldsymbol x}^{\rm T}(t)Q_{i}{\boldsymbol x}(t) < 0, \quad {\boldsymbol x}(t)\in \mathcal{S}, \quad i=1, \cdot\cdot\cdot, p $
(6b) 则一定存在非负标量 $c_i, i=1, \cdot\cdot\cdot, p$ , 使得:
$ \begin{align} Q_0-\sum_{i=1}^{p}c_iQ_i < 0 \end{align} $
(6c) 显然条件 (6c) 可以推出条件 (6a). S-procedure就是通过判断条件 (6c) 的可行性来验证条件 (6a) 是否成立的.一般来说, 条件 (6c) 比条件 (6a) 更容易检验.所以, 通过应用S-procedure理论可以找到检验 (6a) 成立的更有效的方法.
由引理1的结论, 考虑条件 (4c), 当给定 $k$ 时, 令
$ \begin{align*} \begin{array}{l} Q_0=A_{d, k}^{\rm T}E^{\rm T}P(t)A_{d, k}-E^{\rm T}P(t), \quad \mathcal{S}=\mathcal{S}_k \end{array} \end{align*} $
则条件 (4c) 等价于如下不等式:
$ \begin{align*} \begin{array}{l} A_{d, k}^{\rm T}E^{\rm T}P(t)A_{d, k}- E^{\rm T}P(t)-\sum\limits_{i=1}^{p}c_{i, k}(t)Q_{i, k} < 0 \end{array} \end{align*} $
于是可以推出如下定理.
定理3.如果存在对称矩阵集合 $Q_{i, k}, i=1, \cdot\cdot\cdot, p_k, k=1, \cdot\cdot\cdot, {N}$ 满足引理1条件, 并且存在一个连续可微对称非奇异函数矩阵 $P(\cdot)$ 和非负标量 $c_{i, k}(\cdot)\geq 0 $ 有:
$ E^{\rm T}P(t)=P^{\rm T}(t)E\geq 0 $
(7a) $ A^{\rm T}(t)P(t)+P^{\rm T}(t)A(t)+E^{\rm T}\dot{P}(t) < 0 $
(7b) $ \begin{array}{l} A_{d, k}^{\rm T}E^{\rm T}P(t)A_{d, k}- E^{\rm T}P(t)-\sum\limits_{i=1}^{p}c_{i, k}(t)Q_{i, k}<0\\ \qquad {\boldsymbol x}(t)\in \mathcal{S}_k, \quad k=1, 2, \cdot\cdot\cdot, {N} \end{array} $
(7c) $ E^{\rm T}\Gamma(t)\leq E^{\rm T}P(t)\leq E^{\rm T}P(t_0)< E^{\rm T}R $
(7d) 成立, 则系统 (1) 对于 $(c_1, J, R, \Gamma(\cdot))$ 时域稳定.其中 $J=[t_0\quad t_0 +T]$ .
注1.由引理1知定理3的条件有利于这类问题的求解.在定理1中, 跳变时需要解无穷多个矩阵不等式, 而在定理3中, 跳变时只需解在指定集合上的有限个矩阵不等式.同理, 由定理2可以推出如下定理.
定理4.如果存在对称矩阵集合 $Q_{i, k}, i=1, \cdot\cdot\cdot, p_k, k=1, \cdot\cdot\cdot, {N}$ 满足引理1条件, 并且存在一个连续可微对称非奇异函数矩阵 $P(\cdot)$ 和非负标量 $c_{i, k}(\cdot)\geq 0$ 有:
$ E^{\rm T}P(t)=P^{\rm T}(t)E\geq 0 $
(8a) $ \begin{bmatrix} \Pi(t)&P^{\rm T}(t)G(t)\\ G^{\rm T}(t)P(t)&-I \end{bmatrix} < 0 $
(8b) $ \begin{array}{l} A_{d, k}^{\rm T}E^{\rm T}P(t)A_{d, k}-E^{\rm T}P(t)-\sum\limits_{i=1}^{p}c_{i, k}(t)Q_{i, k} < 0\\ \qquad {\boldsymbol x}(t)\in \mathcal{S}_k, \quad k=1, 2, \cdot\cdot\cdot, {N} \end{array} $
(8c) $ E^{\rm T}\Gamma(t)\leq E^{\rm T}P(t)\leq E^{\rm T}P(t_0) < E^{\rm T}R $
(8d) 成立, 则称系统 (2) 对于 $(c_1, c_2, {\boldsymbol \omega}(t), J, R, \Gamma(\cdot))$ 时域稳定.其中 $\Pi(t)$ 与定理2相同.
3. 时域控制器设计
考虑如下状态依赖广义时变脉冲系统
$ \begin{align} \left\{ \begin{array}{l} E\dot{{\boldsymbol x}}(t)=A(t){\boldsymbol x}(t)+G(t){\boldsymbol \omega}(t)+\\ \qquad B(t)u(t), \quad {\boldsymbol x}(t)\notin \mathcal{S}_k\\ {\boldsymbol x}^{+}_{k}(t)=A_{d, k}{\boldsymbol x}(t), \quad {\boldsymbol x}(t)\in \mathcal{S}_k\\ {\boldsymbol x}(t_{0})={\boldsymbol x}_{0}\quad k=1, 2, \cdot\cdot\cdot, {N} \end{array} \right. \end{align} $
(9) 对上述系统找到一个状态反馈控制律
$ \begin{align*} {\boldsymbol u}(t)=K(t){\boldsymbol x}(t) \end{align*} $
使得闭环系统
$ \begin{align} \left\{ \begin{array}{l} E\dot{{\boldsymbol x}}(t)=A_c(t){\boldsymbol x}(t)+G(t){\boldsymbol \omega}(t), \quad {\boldsymbol x}(t)\notin \mathcal{S}_k\\ {\boldsymbol x}^{+}_{k}(t)=A_{d, k}{\boldsymbol x}(t), \quad {\boldsymbol x}(t)\in \mathcal{S}_k\\ {\boldsymbol x}(t_{0})={\boldsymbol x}_{0}, \quad k=1, 2, \cdot\cdot\cdot, {N} \end{array} \right. \end{align} $
(10) 是时域稳定, 其中 $A_c(t)=A(t)+B(t)K(t)$ .
定理5.对于系统 (10), 如果存在分段连续可微对称非奇异的函数矩阵 $\bar{P}(\cdot)$ 、函数矩阵 $L_{k}(\cdot)$ 和非负标量 $C_{i, k}\leq 0$ 满足下列不等式组, $\forall t\in J$ .
$ \begin{bmatrix} \Pi_{1}(t)&G(t)\\ G^{\rm T}(t)&-I \end{bmatrix} < 0 $
(11a) $ \begin{array}{l} A_{d, k}^{\rm T}E^{\rm T}\bar{P}^{-1}(t)A_{d, k}-E^{\rm T}\bar{P}^{-1}(t)-\\ \qquad \quad \sum\limits_{i=1}^{p}c_{i, k}(t)Q_{i, k} < 0\\ \qquad {\boldsymbol x}(t)\in S_k, \quad k=1, 2, \cdot\cdot\cdot, {N} \end{array} $
(11b) $ E^{\rm T}\Gamma(t)\leq E^{\rm T}\bar{P}^{-1}(t)\leq E^{\rm T}\bar{P}^{-1}(t_0) < E^{\rm T}R $
(11c) 则称系统 (10) 对于 $(c_1, c_2, {\boldsymbol\omega}(t), J, R, \Gamma(\cdot))$ 时域稳定, 且状态反馈控制律为
$ \begin{align} K_k(t)=L_k(t)\bar{P}^{-1}(t) \end{align} $
(12) 其中, $\Pi_1(t)=-E\dot{\bar{P}}(t)+\bar{P}^{\rm T}(t)A^{\rm T}(t)+A(t)\bar{P}(t)+L^{\rm T}_{k}(t)B^{\rm T}(t)+B(t)L_{k}(t)$ .
证明.对于 $t\in J_k$ , 将状态反馈控制律 $K_{k}(t)=L_{k}(t)\bar{P}^{-1}(t)$ 带入式 (9), 可以得到闭环系统 (10), 其中, $A_{c}(t)=A(t)+B(t)L_{i}(t)\bar{P}(t)^{-1}$ .显然 (11a) 等价于下列不等式:
$ \begin{align} \left[\begin{array}{cc}\Pi_{2}(t)&G(t)\\ G^{\rm T}(t)&-I\end{array}\right] < 0 \end{align} $
(13) 其中
$ \begin{align*} \Pi_{2}(t)=-E\dot{\bar{P}}(t)+\bar{P}^{\rm T}(t)A_{c}^{\rm T}(t)+A_{c}(t)\bar{P}(t) \end{align*} $
令 $P(t)=\bar{P}^{-1}(t)$ , 将式 (13) 分别左乘 ${\rm diag}\{\bar{P}^{\rm -T}(t), I\}$ , 右乘 ${\rm diag} \{\bar{P}^{-1}(t), I\}$ , 得到下列不等式:
$ \begin{align*} \left[\begin{array}{cc}\Pi_{3}(t)&\bar{P}^{\rm-T}(t)G(t)\\ G^{\rm T}(t)\bar{P}^{-1}(t)&-I\end{array}\right] < 0 \end{align*} $
其中, $ \Pi_{3}(t)=-\bar{P}^{\rm -T}(t)E\dot{\bar{P}}(t)\bar{P}^{-1}(t)+ A_{c}^{\rm T}(t) \bar{P}^{-1}(t)+\bar{P}^{\rm -T}(t)A_{c}(t).$
因为 $P(t)=\bar{P}^{-1}(t)$ , 故
$ \begin{align*} I=\bar{P}(t)P(t), \quad 0=\dot{\bar{P}}(t)P(t)+\bar{P}(t)\dot{P}(t) \end{align*} $
又因为 $E^{\rm T}P(t)=P^{\rm T}(t)E\geq0$ , 我们很容易可以得出:
$ \begin{align*} -P^{\rm T}(t)E\dot{\bar{P}}(t)P(t)=-E^{\rm T}P(t)\dot{\bar{P}}(t)P(t)=E^{\rm T}\dot{P}(t)\end{align*} $
由此可得:
$ \begin{align} \left[\begin{array}{cc}\Pi_{4}(t)&P^{\rm T}(t)G(t)\\ G^{\rm T}(t)P(t)&-I\end{array}\right] < 0 \end{align} $
(14) 其中
$ \begin{align*} \Pi_{4}(t)=E^{\rm T}\dot{P}(t)+A_c^{\rm T}(t)P(t)+P(t)A_c(t) \end{align*} $
另一方面, 因为 $P(t)=\bar{P}^{-1}(t)$ , 条件 (11b) 和 (11c) 等价于式 (7c) 和 (7d).综上所述, 闭环系统 (10) 是对于 $(c_1, c_2, {\boldsymbol\omega}(t), J, R, \Gamma(\cdot))$ 时域稳定的.
为了将小区间内的时变矩阵不等式转化为标准的矩阵不等式组.可以将小区间内的时变矩阵不等式做如下处理.假设 $P(t)$ (或 $\bar{P}(t)$ ) 是分段线性的, $P(t)$ (或 $\bar{P}(t)$ ) 在 $\mathcal{T}_{x(\cdot)}$ 处发生跳变 (以下只给出 $P(t)$ (或 $\bar{P}(t)$ ) 的形式, $L(t)$ 、 $\dot{P}(t)$ 形式与 $P(t)$ 类似).
$ \begin{align*} \label{eq} \left\{ \begin{aligned} & P(0)({\rm or}\ (\bar{P}(0)))=\Pi_{1}^{0}\\ & P(t)({\rm or}\ (\bar{P}(t)))=\Pi_{k}^{0}+\Pi_{k}^{s}(t-(k-1)T_{s}), \\ & \qquad \qquad k\in N : kx \bar{k}, \quad t\in[(k-1)T_{s}, kT_{s}]\\ & P(t)({\rm or}\ (\bar{P}(t)))=\Pi_{\bar{k}+1}^{0}+\Pi_{\bar{k}+1}^{0}(t-\bar{k}T_{s}), t\in[\bar{k}T_{s}, T] \end{aligned} \right. \end{align*} $
因此上述条件可以转化为一组标准的矩阵不等式求解问题.由于 $E^{\rm T}P(t)=P^{\rm T}(t)E\geq0$ ( $E^{\rm T}\Pi_{k}^{0}=\Pi_{k}^{0\rm T}E\geq0$ $E^{\rm T}\Pi_{k}^{s}=\Pi_{k}^{s{\rm T}}E\geq0$ ) 是一组非严格的矩阵不等式, 这样对于求解会造成一定的麻烦.为了将非严格的矩阵不等式组转化为严格的矩阵不等式组, 我们介绍如下引理.
引理2[31].如果 $X\in \boldsymbol{R}^{n\times n}$ 是对称矩阵且满足 $E_{L}^{\rm T}XE_{L}>0$ , $T\in {\bf R }^{(n-r)\times(n-r)}$ 是非奇异矩阵.则 $XE+M^{\rm T}TS^{\rm T}$ 也是非奇异的且它的逆可以表示为
$ \begin{align*} (XE+M^{\rm T}TS^{\rm T})^{-1}=XE^{\rm T}+STM \end{align*} $
其中, $X$ 是对称矩阵, $T$ 是非奇异矩阵.
$ \begin{align*} E_{R}^{\rm T}XE_{R}=(E_{L}^{\rm T}XE_{L})^{-1}, \ T=(S^{\rm T}S)^{-1}T^{-1}(MM^{\rm T})^{-1}\end{align*} $
$M$ 和 $S$ 是行满秩矩阵满足 $ME=0$ , $ES=0$ ; $E$ 可以分解为 $E=E_{L}E_{R}^{\rm T}$ , 其中 $E_{L}\in \boldsymbol{R}^{n\times r}$ , $E_{R}\in {\bf R }^{n\times r}$ 是列满秩的.
令 $\Pi_{k}^{0}=X_{k}^{0}E+M^{\rm T}T_{k}^{0}S^{\rm T}$ , $\Pi_{k}^{s}=X_{k}^{s}E+M^{\rm T}T_{k}^{s}S^{\rm T}$ .根据引理2可以得到 $(X_{k}^{0}E+M^{\rm T}T_{k}^{0}S^{\rm T})^{-1}=X_{k}^{0}E^{\rm T}+ST_{k}^{0}M$ 和 $(X_{k}^{s}E+M^{\rm T}T_{k}^{s}S^{\rm T})^{-1}=X_{k}^{s}E^{\rm T}+ST_{k}^{0}M$ .这样 $E^{\rm T}P(t)=P^{\rm T}(t)E\geq0$ 就得到了满足.因此, 非严格的矩阵不等式组转化为了严格的矩阵不等式组.利用Matlab LMI工具箱, 就可以对 $X_{k}^{s}, T_{k}^{0}, T_{k}^{s}, X_{k}^{0}$ (或 $X_{k}^{0}, X_{k}^{s}, T_{k}^{0}, T_{k}^{s}), \Lambda_{k}^{0}, \Lambda_{k}^{s}$ 进行求解, 从而得到 $P(t)$ (或 $(\bar{P}(t))$ 和 $L(t)$ .
4. 数值算例
例1.考虑广义时变脉冲系统 (9),
$ \begin{align*} &E=\left[\begin{array}{ccc} 1&0\\0&0 \end{array}\right], \quad A=\left[\begin{array}{ccc} 1&-1.5\\0.5&t \end{array}\right]\\ &A_{d, 1}=\left[\begin{array}{ccc} 0.8&0\\-1&0.5 \end{array}\right], \quad G=\left[\begin{array}{ccc} 1\\1 \end{array}\right] B=\left[\begin{array}{ccc} 0\\1 \end{array}\right] \end{align*} $
跳变集合
$ \begin{align*} \mathcal{S}_1= \left(\begin{array}{*{20}c}\left(\begin{array}{*{20}c}0.5\\ 0.2\end{array}\right), &\left(\begin{array}{*{20}c}0.4\\ 0.4 \end{array}\right)\end{array}\right) \end{align*} $
其中, 选取 ${\boldsymbol\omega}(t)=1$ , $J=[0 {\rm s}\quad 5 {\rm s}]$ , $R=\left[{array}{ccc} 2&0\\0&2 {array}\right]$ , $c_1=3$ , $c_2=4$ .由引理1可选取
$ \begin{align*} Q=\left[\begin{array}{ccc} 0.4000&-0.7000\\-0.7000&1.0000 \end{array}\right]\end{align*} $
显然
$ \begin{align*} E_{R}=E_{L}=\left[\begin{array}{ccc} 1\\0 \end{array}\right] \end{align*} $
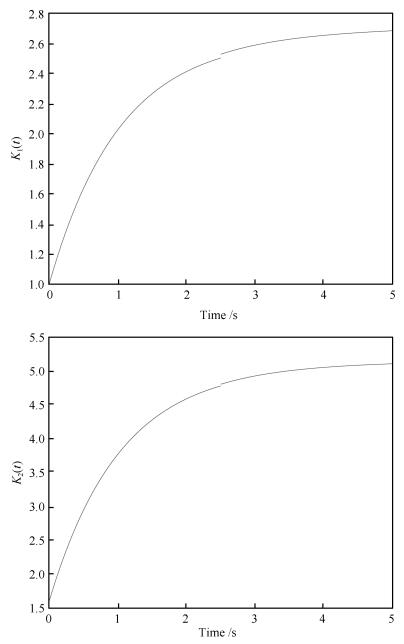
我们选 $M^{\rm T}=S=[0 \quad 1]^{\rm T}$ .则存在 $\Gamma(t)=\left[{array}{ccc} 1&0\\0&1{array}\right]$ , 根据Matlab LMI工具箱求解矩阵不等式组, 可得正数 $c_1(\cdot)$ 及矩阵 $P(\cdot), L_1(\cdot)$ , 使得式 (11) 成立, 则闭环系统 (10) 是时域稳定的, 且状态反馈控制律 $K(t)=[K_1(t)\quad K_2(t)]$ 见图 1.
5. 结论
本文针对状态依赖广义时变脉冲系统时域稳定问题进行研究, 给出了广义时变脉冲系统时域稳定充分条件及状态反馈控制器的设计.并且对上述充分条件提出DLMIs优化计算的方法, 使得这类问题在数值计算上易于处理.利用分段线性化将小区间内广义时变矩阵不等式转化为广义时不变线性矩阵不等式来求解.最后给出数值算例来验证结论的有效性.
-
[1] Duan G R. Analysis and Design of Descriptor Linear Systems. New York:Springer Verlag, 2010. [2] Rosenbrock H H. Structural properties of linear dynamical systems. International Journal of Control, 1974, 20(2):191-202 doi: 10.1080/00207177408932729 [3] Jeung E T, Kim J H, Park H B. H∞-output feedback controller design for linear systems with time-varying delayed state. IEEE Transactions on Automatic Control, 1998, 43(7):971-974 doi: 10.1109/9.701103 [4] Campell S L, Petzold L R. Canonical forms and solvable singular systems of differential equations. SIAM Journal of Algebraic Discrete Methods, 1983, 4(4):517-521 doi: 10.1137/0604051 [5] Takaba K, Morihira N, Katayama T. H∞ control for descriptor systems-a J-spectral factorization approach. In:Proceedings of the 33rd IEEE Conference on Decision and Control. Lake Buena Vista, USA:IEEE, 1994, 3:2251-2256 [6] Zhao Z H, Zhang Q L, Liu X D. H∞ control and parametric controllers for descriptor systems. In:Proceedings of the 2002 American Control Confernece. Anchorage, USA:IEEE, 2002, 6:4908-4913 [7] 苏晓明, 吕明珠.广义不确定周期时变系统的鲁棒稳定性分析.自动化学报, 2006, 32(4):481-488 http://www.aas.net.cn/CN/abstract/abstract14387.shtmlSu Xiao-Ming, Lv Ming-Zhu. Analysis of robust stability for linear time-varying uncertain periodic descriptor systems. Acta Automatica Sinica, 2006, 32(4):481-488 http://www.aas.net.cn/CN/abstract/abstract14387.shtml [8] 苏晓明, 王刚, 吕明珠.广义不确定周期时变系统的鲁棒镇定控制.东北大学学报 (自然科学版), 2006, 27(7):716-719 http://www.cnki.com.cn/Article/CJFDTOTAL-DBDX200607003.htmSu Xiao-Ming, Wang Gang, Lv Ming-Zhu. Robust stabilization control for generalized periodically time-varying uncertain descriptor systems. Journal of Northeastern University (Natural Science), 2006, 27(7):716-719 http://www.cnki.com.cn/Article/CJFDTOTAL-DBDX200607003.htm [9] 王刚, 苏晓明, 孟飞.一般广义时变系统的容许性和二次容许性.控制与决策, 2014, 29(2):221-225 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201402005.htmWang Gang, Su Xiao-Ming, Meng Fei. Admissibility and quadratic admissibility for time-varying general singular system. Control and Decision, 2014, 29(2):221-225 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201402005.htm [10] 艾玲.线性时变广义系统的脉冲控制.哈尔滨理工大学学报, 2004, 9(4):119-121 http://www.cnki.com.cn/Article/CJFDTOTAL-HLGX200404032.htmAi Ling. Impulse controllability of linear time-varying singular systems. Journal of Harbin University of Science and Technology, 2004, 9(4):119-121 http://www.cnki.com.cn/Article/CJFDTOTAL-HLGX200404032.htm [11] Kamenkov G V. On stability of motion over a finite interval of time. Akad Nauk SSSR Prikl Mat Meh, 1953, 17:529-540 [12] Dorato P. Short-time Stability in Linear Time-Varying Systems, Polytechnic Inst of Brooklyn N Y Microwave Research Inst, 1961. [13] Kablar N A. Finite-time stability of time-varying linear singular systems. In:Proceedings of the 37th IEEE Conference on Decision and Control. Tampa, USA:IEEE, 1998, 4:3831-3836 [14] Garcia G, Tarbouriech S, Bernussou J. Finite-time stabilization of linear time-varying continuous systems. IEEE Transactions on Automatic Control, 2009, 54(2):364-369 doi: 10.1109/TAC.2008.2008325 [15] Amato F, Ariola M, Cosentino C. Finite-time stability of linear time-varying systems:analysis and controller design. IEEE Transactions on Automatic Control, 2010, 55(4):1003-1008 doi: 10.1109/TAC.2010.2041680 [16] Liu L, Sun J T. Finite-time stabilization of linear systems via impulsive control. International Journal of Control, 2008, 81(6):905-909 doi: 10.1080/00207170701519060 [17] 孙继涛.脉冲系统的分析与控制.北京:科学出版社, 2013.Sun J T. Analysis and Control of Impulsive System. Beijing:Science Press, 2013. [18] Tong Y X, Wu B W, Huang F. Finite-time boundedness and L2-gain analysis for linear time-varying singular impulsive systems. In:Proceedings of the 24th Chinese Control and Decision Conference. Taiyuan, China:IEEE, 2012. 4031-4035 [19] Amato F, Ariola M, Dorato P. Finite-time control of linear systems subject to parametric uncertainties and disturbances. Automatica, 2001, 37(9):1459-1463 doi: 10.1016/S0005-1098(01)00087-5 [20] Feng J E, Wu Z, Sun J B. Finite-time control of linear singular systems with parametric uncertainties and disturbances. Acta Automatica Sinica, 2005, 31(4):634-637 [21] Zhao S W, Sun J T, Liu L. Finite-time stability of linear time-varying singular systems with impulsive effects. International Journal of Control, 2008, 81(11):1824-1829 doi: 10.1080/00207170801898893 [22] Xu J, Sun J. Finite-time stability of linear time-varying singular impulsive systems. IET Control Theory and Applications, 2010, 4(10):2239-2244 doi: 10.1049/iet-cta.2010.0242 [23] Amato F, Ambrosino R, Ariola M, Cosentino C. Finite-time stability of linear time-varying systems with jumps. Automatica, 2009, 45(5):1354-1358 doi: 10.1016/j.automatica.2008.12.016 [24] Amato F, Ambrosino R, Ariola M, Calabrese F, Cosentino C. Finite-time stability of linear time-varying systems with jumps:analysis and controller design. In:Proceeding of the 2008 American Control Conference. Seattle, USA:IEEE, 2008. 1638-1643 [25] Ambrosino R, Calabrese F, Cosentino C, De Tommasi G. Sufficient conditions for finite-time stability of impulsive dynamical systems. IEEE Transactions on Automatic Control, 2009, 54(4):861-865 doi: 10.1109/TAC.2008.2010965 [26] Amato F, Ambrosino R, Cosentino C, De Tommasi G. Finite-time stabilization of impulsive dynamical linear systems. Nonlinear Analysis:Hybrid Systems, 2011, 5(1):89-101 doi: 10.1016/j.nahs.2010.10.001 [27] Amato F, Ambrosino R, Ariola M, De Tommasi G. Robust finite-time stability of impulsive dynamical linear systems subject to norm-bounded uncertainties. International Journal of Robust and Nonlinear Control, 2011, 21(10):1080-1092 doi: 10.1002/rnc.1620 [28] Amato F, De Tommasi G, Pironti A. Necessary and sufficient conditions for finite-time stability of impulsive dynamical linear systems. Automatica, 2013, 49(8):2546-2550 doi: 10.1016/j.automatica.2013.04.004 [29] Amato F, Ambrosino R, Ariola M, Cosentino C, De Tommasi G. Finite-Time Stability and Control. London:Springer-Verlag, 2014. [30] Boyd S, El Ghaoui L, Feron E, Balakrishnan V. Linear Matrix Inequalities in System and Control Theory. Philadelphia, USA:SIAM, 1994. [31] 苏晓明, 阿迪亚.广义时变脉冲系统的输入输出时域稳定.自动化学报, 2014, 40(11):2512-2520 http://www.aas.net.cn/CN/abstract/abstract18527.shtmlSu Xiao-Ming, Adiya. Input-output finite-time stability of linear time-varying descriptor impulse systems. Acta Automatica Sinica, 2014, 40(11):2512-2520 http://www.aas.net.cn/CN/abstract/abstract18527.shtml -





 下载:
下载:
 下载:
下载:
